ОБ ОДНОМ СЛУЧАЕ ИССЛЕДОВАНИЯ ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ МЕТОДОМ ПРИБЛИЖЕННЫХ ТОЧЕЧНЫХ ОТОБРАЖЕНИЙ
DOI: https://doi.org/10.23670/IRJ.2018.74.8.001
ОБ ОДНОМ СЛУЧАЕ ИССЛЕДОВАНИЯ ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ МЕТОДОМ ПРИБЛИЖЕННЫХ ТОЧЕЧНЫХ ОТОБРАЖЕНИЙ
Научная статья
Антоновская О.Г.1, *, Зайцева М.Н.2
1 ORCID: 0000-0002-5688-7996,
Нижегородский государственный архитектурно-строительный университет, Нижний Новгород, Россия;
2 ORCID: 0000-0002-3649-0385,
Нижегородский государственный автомеханический техникум, Нижний Новгород, Россия
* Корреспондирующий автор (olga.antonovsckaja[at]yandex.ru)
Аннотация
Рассматривается вопрос о возможности исследования синхронизации квазигармонического осциллятора с нелинейностью типа кубической параболы методом приближенных точечных отображений. Вопрос о синхронизации квазигармонического осциллятора сводится к решению вопроса о существовании неподвижных точек точечного отображения, при построении которого применяется метод последовательных приближений. Предложенный метод исследования является асимптотическим методом, поэтому важным является также вопрос о применимости результатов приближенного исследования при конкретных значениях малого параметра. В настоящей статье предложено рассматривать задачу о применимости результатов приближенного исследования, оценивая степень близости приближенного точечного отображения к точному отображению.
Ключевые слова: квазигармонический осциллятор, малый параметр, асимптотические методы исследования, метод точечных отображений.
ON INVESTIGATION OF FORCED SYNCHRONIZATION BY THE METHOD OF APPROXIMATED POINT MAPPINGS
Research article
Antonovskaya O.G.1, *, Zaytseva M.N.2
1 ORCID: 0000-0002-5688-7996,
Nizhny Novgorod State University of Architecture and Civil Engineering, Nizhny Novgorod, Russia;
2 ORCID: 0000-0002-3649-0385,
Nizhny Novgorod State Automotive Technical College, Nizhny Novgorod, Russia
* Corresponding author (olga.antonovsckaja[at]yandex.ru)
Abstract
The article considers the possibility of investigating the synchronization of a quasiharmonic oscillator with nonlinearity of the type of a cubic parabola by the method of approximate point mappings. The synchronization of a quasiharmonic oscillator comes to solving the problem of the existence of fixed points on a point map, while the method of successive approximations is applied for their construction. The proposed method of investigation is an asymptotic method; therefore, the applicability of the results of an approximate investigation at specific values of the small parameter is also important. In this paper, we propose to consider the problem of applicability of the results of an approximate investigation, estimating the degree of closeness of the approximate point mapping to the exact mapping.
Keywords: quasiharmonic oscillator, small parameter, asymptotic methods of investigation, method of point mappings.
С точки зрения современной науки изучение нелинейной колебательной системы означает разбиение ее фазового пространства на траектории всех возможных типов, а в пространстве параметров выделение областей, соответствующих существованию движений того или иного типа. При этом в общем случае динамическая система может обладать весьма сложными и разнообразными типами движений, а структура ее фазового пространства и зависимость этой структуры от параметров могут быть очень сложными и трудно исследуемыми.
Совершенно естественно, что наиболее доступными для исследования являются колебательные системы с малой нелинейностью, поскольку к ним в той или иной форме можно применять методы теории возмущений. Поэтому для слабо нелинейных систем имеется ряд достаточно общих асимптотических методов, применимых ко многим типичным классам колебательных систем. Основными из них являются метод малого параметра и метод усреднения, а также методы Н. Н. Боголюбова и Н. М. Крылова, представляющие собой развитие метода усреднения и получение оценок более высокого порядка [1].
Следует отметить, что до сих пор особый интерес представляет изучение систем, близких к гармоническому осциллятору (квазигармонический осциллятор) [1, С. 19–21], [2, С. 650–663]. Одним из важных достоинств такой системы является возможность использовать хорошо известные математические свойства процессов колебаний гармонического осциллятора с медленно меняющейся частотой в различного вида задачах: от задач обработки сигналов [3] до исследования неравновесных экономических систем [4].
В настоящей работе приведен пример исследования квазигармонического осциллятора (с нелинейностью вида кубической параболы) методом приближенных точечных отображений [5], [6]: вопрос о его синхронизации сводится к решению вопроса о существовании неподвижных точек точечного отображения, при построении которого применяется метод последовательных приближений. Обсуждается вопрос о локальной применимости результатов приближенного исследования.
Известно [5], [6, С. 5–6], что при исследовании динамики синхронизуемого осциллятора
![]() , (1)
, (1)
в котором 0 < μ << 1 , а 2pπ - период внешней силы, методом точечных отображений [7], исследование поведения траекторий (1) может быть сведено к изучению точечного отображения T секущей поверхности ![]() фазового пространства
фазового пространства ![]() в себя [5] (или секущей поверхности t = 0 в секущую поверхность
в себя [5] (или секущей поверхности t = 0 в секущую поверхность ![]() ), порожденного траекториями системы. При этом с точностью до величин порядка μ2 точечное отображение T может быть приближено точечным отображением
), порожденного траекториями системы. При этом с точностью до величин порядка μ2 точечное отображение T может быть приближено точечным отображением ![]() с функциями последования
с функциями последования
![]() (2)
(2)
![]() (3)
(3)
где
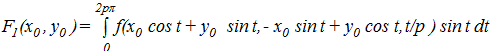 , (4)
, (4)
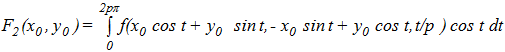 . (5)
. (5)
Поскольку формулы (2)–(5) явные, изучение условий существования синхронного режима с периодом внешней силы может быть проведено с помощью изучения условий существования и устойчивости простой неподвижной точки ![]() приближенного точечного отображения
приближенного точечного отображения ![]() .
.
Рассмотрим уравнение синхронизуемого осциллятора с нелинейностью вида кубической параболы
![]() (6)
(6)
где 0<μ<<1, A>0, или, если ввести y = x, систему двух уравнений первого порядка
![]() (7)
(7)
Задача состоит в установлении условий существования у (7) периодического решения с периодом 2π.
В этом случае точечное отображение ![]() , приближающее отображение T секущей поверхности t = 0 фазового пространства x, y = x, t в секущую поверхность
, приближающее отображение T секущей поверхности t = 0 фазового пространства x, y = x, t в секущую поверхность ![]() , порождаемое траекториями системы (7), с точностью до членов порядка имеет вид
, порождаемое траекториями системы (7), с точностью до членов порядка имеет вид
![]() (8)
(8)
![]() (9)
(9)
Условия существования неподвижной точки точечного отображения (8)–(9) дают соотношения
![]() (10)
(10)
где ![]() находится из уравнения
находится из уравнения
![]() (11)
(11)
То есть факт существования (10) неподвижных точек ![]() определяется фактом существования корней
определяется фактом существования корней ![]() у (11).
у (11).
Детальный анализ уравнения (11) позволяет получить картину резонансных кривых при различных значениях ![]() (рис. 1–2). В самом деле, при
(рис. 1–2). В самом деле, при ![]() уравнение (11) имеет единственный корень
уравнение (11) имеет единственный корень ![]() , причем при
, причем при ![]() . Т.е. при
. Т.е. при ![]() резонансная кривая является разомкнутой для любого A (рис. 1). В случае
резонансная кривая является разомкнутой для любого A (рис. 1). В случае ![]() для значений
для значений ![]() при
при ![]() существует три корня уравнения (11)
существует три корня уравнения (11) ![]() , два из которых сливаются между собой при
, два из которых сливаются между собой при ![]() и исчезают через значение
и исчезают через значение ![]() . При
. При![]() для малых ξ существует единственный корень
для малых ξ существует единственный корень ![]() уравнения (11), с ростом ξ корней становится три, а затем вновь один. При
уравнения (11), с ростом ξ корней становится три, а затем вновь один. При ![]() существует единственный корень
существует единственный корень ![]() уравнения (11). Кроме того, следует отметить, что резонансная кривая имеет горизонтальную касательную при
уравнения (11). Кроме того, следует отметить, что резонансная кривая имеет горизонтальную касательную при ![]() , а вертикальную – в точках кривой
, а вертикальную – в точках кривой
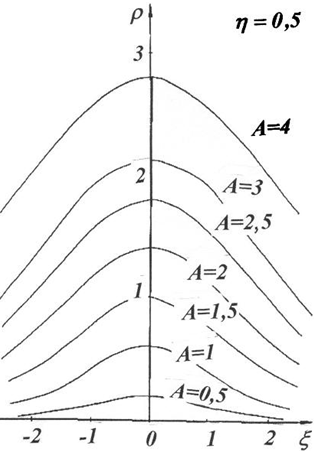
Рис. 1 – Вид резонансных кривых при ![]()
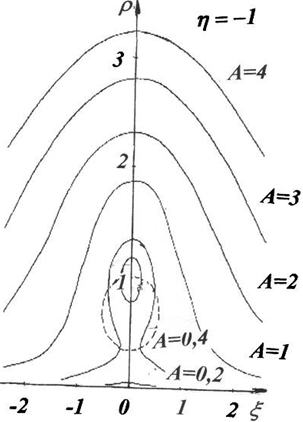
Рис. 2 – Вид резонансных кривых при ![]()
![]() , (12)
, (12)
которая существует только при ![]() и представляет собой эллипс с центром в точке
и представляет собой эллипс с центром в точке ![]() , и с главными диаметрами
, и с главными диаметрами ![]() соответственно. Т.е. при
соответственно. Т.е. при ![]() резонансная кривая имеет две ветви – замкнутую и разомкнутую – при
резонансная кривая имеет две ветви – замкнутую и разомкнутую – при ![]() . При
. При ![]() замкнутая и разомкнутая ветви сливаются, образуя единственную разомкнутую ветвь при
замкнутая и разомкнутая ветви сливаются, образуя единственную разомкнутую ветвь при ![]() (рис. 2).
(рис. 2).
Устойчивость неподвижных точек точечного отображения ![]() в случае их существования определяется корнями характеристического полинома
в случае их существования определяется корнями характеристического полинома
![]() . (13)
. (13)
Корни полинома P(z) (13) будут действительными при ![]() и комплексно-сопряженными при
и комплексно-сопряженными при ![]() , т.е. граница
, т.е. граница ![]() , соответствующая уходу пары корней характеристического полинома с действительной оси в этом случае будет иметь вид двух полупрямых
, соответствующая уходу пары корней характеристического полинома с действительной оси в этом случае будет иметь вид двух полупрямых
![]() (14)
(14)
Уравнения границ ![]() области устойчивости на плоскости ξ, имеют следующий вид.
области устойчивости на плоскости ξ, имеют следующий вид.
Для ![]() получаем уравнение (14).
получаем уравнение (14).
Уравнение ![]() есть
есть
![]() (15)
(15)
Т.е. граница существует при ![]() только для значений
только для значений ![]() и представляет собой эллипс с центром в точке
и представляет собой эллипс с центром в точке ![]() и главными диаметрами
и главными диаметрами ![]() , целиком лежащий в области
, целиком лежащий в области ![]() .
.
Уравнение границы ![]() в предположении, что
в предположении, что ![]() , есть
, есть
![]() , (16)
, (16)
т.е. ![]() в случае ее существования представляет собой куски эллипса с центром в точке
в случае ее существования представляет собой куски эллипса с центром в точке ![]() и главными диаметрами по ξ и по ρ, принадлежащие области
и главными диаметрами по ξ и по ρ, принадлежащие области ![]() . Заметим, что при
. Заметим, что при ![]() всегда имеет точку пересечения с осью
всегда имеет точку пересечения с осью ![]() , которой соответствует
, которой соответствует ![]() .
.
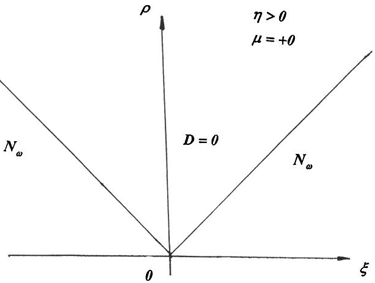
Рис. 3 – Картина D-разбиения при ![]()
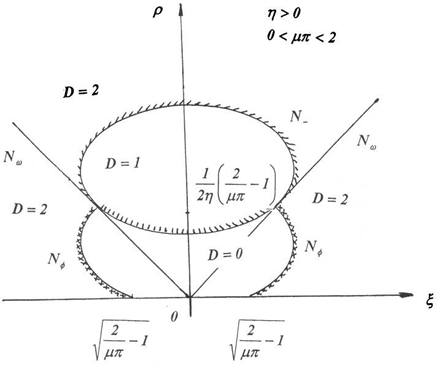
Рис. 4 – Картина D-разбиения при ![]()
Анализ существования и взаимного расположения границ ![]() (14)–(16) позволил получить картину D-разбиения при различных значениях η и малых μ (рис. 3–6). Границы D-разбиения приведены с соответствующей штриховкой в сторону выхода корней характеристического уравнения из единичного круга. Однократная штриховка соответствует бифуркации корней на действительной оси, двойная – бифуркации комплексно-сопряженных корней. Область D=0 есть область устойчивости.
(14)–(16) позволил получить картину D-разбиения при различных значениях η и малых μ (рис. 3–6). Границы D-разбиения приведены с соответствующей штриховкой в сторону выхода корней характеристического уравнения из единичного круга. Однократная штриховка соответствует бифуркации корней на действительной оси, двойная – бифуркации комплексно-сопряженных корней. Область D=0 есть область устойчивости.
Следует отметить, что можно построить границы ![]() и при не малых значениях μ, рассматривая изучение свойств точечного отображения
и при не малых значениях μ, рассматривая изучение свойств точечного отображения ![]() как самостоятельную задачу [5].
как самостоятельную задачу [5].
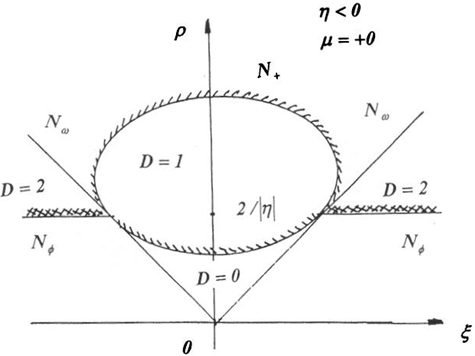
Рис. 5 – Картина D-разбиения при ![]()
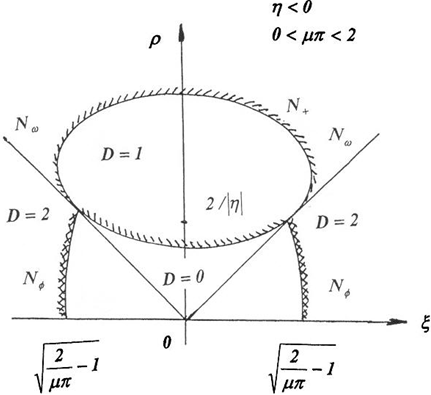
Рис. 6 – Картина D-разбиения при ![]()
В случае ![]() при
при ![]() уходят в бесконечность, а при сжимаются в точку
уходят в бесконечность, а при сжимаются в точку ![]() . При
. При ![]() всегда существует такое значение
всегда существует такое значение ![]() , что для
, что для ![]() неподвижная точка
неподвижная точка ![]() перестает быть устойчивой при малых ξ. Значение
перестает быть устойчивой при малых ξ. Значение ![]() находится из условия касания резонансной кривой границы
находится из условия касания резонансной кривой границы ![]() в точке
в точке ![]() , и равно
, и равно
![]() (17)
(17)
При ![]() границами области устойчивости при
границами области устойчивости при ![]() являются
являются ![]() , причем при
, причем при ![]() кривая
кривая ![]() стремится к прямой
стремится к прямой ![]() , а при
, а при ![]() принимает вид эллипса, проходящего через точку
принимает вид эллипса, проходящего через точку ![]() и точки касания границы
и точки касания границы ![]() полупрямых
полупрямых ![]() . То есть при устойчивая неподвижная точка
. То есть при устойчивая неподвижная точка ![]() всегда существует при малых ξ для
всегда существует при малых ξ для ![]() .
.
Факт существования неподвижных точек точечного отображения ![]() с некоторым характером устойчивости при A=const и различных ξ может быть установлен наложением картины поведения границ областей существования различных типов неподвижных точек на плоскости
с некоторым характером устойчивости при A=const и различных ξ может быть установлен наложением картины поведения границ областей существования различных типов неподвижных точек на плоскости ![]() при заданном μ на плоскость с резонансной кривой при заданном A.
при заданном μ на плоскость с резонансной кривой при заданном A.
Таким образом, во-первых, область устойчивости является ограниченной при любом конечном, хотя и малом μ, все более расширяясь при ![]() . Во-вторых, при переходе на плоскости
. Во-вторых, при переходе на плоскости ![]() через границу N- имеет место серия бифуркаций удвоения периода и переход к хаосу (рис.7), т.е. при
через границу N- имеет место серия бифуркаций удвоения периода и переход к хаосу (рис.7), т.е. при ![]() существует множество примыкающих друг к другу и все более сжимающихся областей, соответствующих режимам кратности 2, 4, 8, 16 и т.д., переходящих с ростом ρ в область хаоса, таких, что попадание резонансной кривой в соответствующую область означает существование периодического режима определенной кратности. Границы
существует множество примыкающих друг к другу и все более сжимающихся областей, соответствующих режимам кратности 2, 4, 8, 16 и т.д., переходящих с ростом ρ в область хаоса, таких, что попадание резонансной кривой в соответствующую область означает существование периодического режима определенной кратности. Границы ![]() этих областей сходятся в общие точки, являющиеся точками стыковки границ
этих областей сходятся в общие точки, являющиеся точками стыковки границ ![]() .
.
Необходимо также отметить, что устойчивый режим, в случае его существования, имеет в фазовом пространстве отображения ![]() ограниченную область притяжения, расширяющуюся при
ограниченную область притяжения, расширяющуюся при ![]() . При дальнейшем движении по резонансным кривым при ξ=const в сторону увеличения ρ, после перехода через границу
. При дальнейшем движении по резонансным кривым при ξ=const в сторону увеличения ρ, после перехода через границу ![]() , которая, по-видимому, является границей вырождения математической модели, ограниченного притягивающего множества в фазовом пространстве не обнаружено. Устойчивость бесконечности в этом случае может быть доказана следующим образом.
, которая, по-видимому, является границей вырождения математической модели, ограниченного притягивающего множества в фазовом пространстве не обнаружено. Устойчивость бесконечности в этом случае может быть доказана следующим образом.
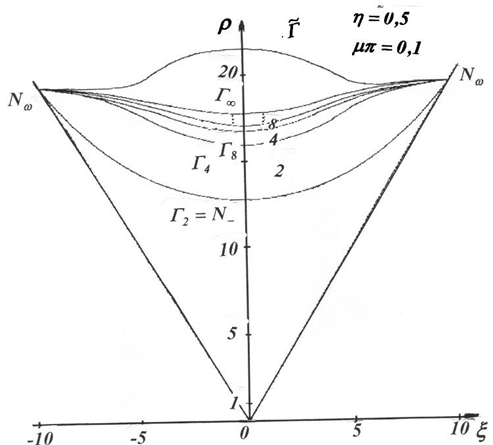
Рис. 7 – Границы областей, соответствующих кратным режимам
Рассмотрим простейшую функцию Ляпунова
![]() . (18)
. (18)
Ее первая разность в силу формул (8) –(9) будет удовлетворять условию
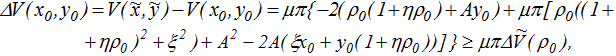 (19)
(19)
где
![]() (20)
(20)
При любом конечном, хотя и малом, значении μ определяющим членом ![]() является
является ![]() (19), поскольку все прочие члены имеют меньший порядок. Таким образом,
(19), поскольку все прочие члены имеют меньший порядок. Таким образом, ![]() становится положительной при
становится положительной при ![]() . В самом деле, согласно (20),
. В самом деле, согласно (20), ![]() где
где
![]() . (21)
. (21)
а значит бесконечность всегда устойчива.
Область хаоса не является сплошной. В ней имеются "окна" [8 С. 272–275], в которых существуют режимы различной кратности. Об этом свидетельствуют данные, приведенные на рис. 8, где указаны граничные значения A, соответствующие областям кратных режимов ("окнам"). Последовательность найденных кратностей очень напоминает порядок смены кратностей неподвижных точек для одномерного отображения, установленный А.Н.Шарковским [9]. Причем переход к хаосу из этих окон может сопровождаться, а может не сопровождаться удвоением периода.

Рис. 8 – Пример структуры области хаоса
Заметим, что задача нахождения условий существования у квазигармонического осциллятора периодического решения с периодом 2π решается как задача нахождения условий существования неподвижных точек с определенным характером устойчивости у приближенно построенного точечного отображения ![]() , и выводы относительно существования и характера устойчивости неподвижных точек в приведенных выше исследованиях (а значит и соответствующих им периодических решений исходной системы) были сделаны на основе изучения свойств аппроксимирующего точечного отображения. При этом естественно встает вопрос об адекватности поведения траекторий точного и приближенного точечных отображений, т.е. о применимости полученных результатов [6, С. 81–88]. И, подобно [10], для решения этого вопроса можно воспользоваться результатами работы [5], [6, С. 123–135], и рассматривать задачу о применимости результатов приближенного исследования, оценивая степень близости приближенного точечного отображения к точному отображению.
, и выводы относительно существования и характера устойчивости неподвижных точек в приведенных выше исследованиях (а значит и соответствующих им периодических решений исходной системы) были сделаны на основе изучения свойств аппроксимирующего точечного отображения. При этом естественно встает вопрос об адекватности поведения траекторий точного и приближенного точечных отображений, т.е. о применимости полученных результатов [6, С. 81–88]. И, подобно [10], для решения этого вопроса можно воспользоваться результатами работы [5], [6, С. 123–135], и рассматривать задачу о применимости результатов приближенного исследования, оценивая степень близости приближенного точечного отображения к точному отображению.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Боголюбов Н. Н. Асимптотические методы в теории нелинейных колебаний / Н. Н. Боголюбов, Ю. А. Митропольский. – М.: Наука, 1974. – 504 с.
- Андронов А. А. Теория колебаний / А. А. Андронов, А. А. Витт, С. Э. Хайкин. – М.: Физматгиз, 1959. – 916 с.
- Журавлев В. М. Построение огибающей и локальной частоты стохастического процесса на основе модели осциллятора с флуктуирующей частотой / В. М. Журавлев, П. П. Миронов, С. В. Летуновский // Изв. вузов. Поволжский регион. Физико-математические науки. – 2013. –№3(27). – С. 159–169.
- Ивинская Е. Ю. Теоретические аспекты исследования неравновесных экономических систем на основе модели гармонического осциллятора / Е. Ю. Ивинская // Теория и практика общественного развития. Экономические науки. – 2015. – № 21. – С. 57–59.
- Антоновская О. Г. О влиянии насыщения нелинейности на результаты исследования принудительной синхронизации методом приближенных точечных отображений / О. Г. Антоновская // Математическое моделирование и оптимальное управление: Вестник ННГУ, Нижний Новгород. – 1999. – № 2(21). – С. 198–208.
- Антоновская О. Г. Метод точечных отображений в задачах нелинейной дингамики / О. Г. Антоновская, В.И. Горюнов. – Гамбург: LAP Lambert Academic Publishing, 2013. – 140 с.
- Неймарк Ю. И. Метод точечных отображений в теории нелинейных колебаний / Ю. И. Неймарк. – М.: Наука, 1972. – 472 с.
- Неймарк Ю. И. Стохастические и хаотические колебания / Ю. И. Неймарк, П. С. Ланда. – М.: Наука, 1987. – 424 с.
- Шарковский А. Н. Сосуществование циклов непрерывного преобразования прямой в себя / А. Н. Шарковский // Укр. мат. журн. – 1964. – Т.26. – № 1. – С. 61–71.
- Антоновская О. Г. О приближенном исследовании близкого к тождественному точечного отображения плоскости в плоскость / О. Г. Антоновская // Математическое моделирование и оптимальное управление: Вестник ННГУ, Нижний Новгород. – 2004. – № 1(27). – С. 63–69.
Список литературы на английском языке / References in English
- Bogolyubov N. N. Asimptotichesiye metody v teorii nelineynyh kolebaniy [Asymptotic methods in nonlinear vibrations theory] / N. N. Bogolyubov, A. Yu. Mitropolskiy – M.: Nauka, 1974. – 504 p. [in Russian]
- Andronov A. A. Teoriya kolebaniy [Vibrations theory] / A. A. Andronov, A. A. Vitt, S. Yu. Haykin. – M.: Fizmatgiz, 1959. – 916 p. [in Russian]
- Zhuravlev V. M. Postroeniye ogibayushey b lokalnoy chastity stohasticheskogo protsessa na osnove modeli ossillyatora c fluktuiruyushey chastoty [The construction of envelope and local frequency of stochastic processon the base of oscillator with fluctuating frequency] / V. M. Zhuravlev, P. P. Mironov, S. V. Letunovskiy // Izv. Vuzov. Povolzhskiy region. Fiziko-matematicheskiye nauki. [Higher educational proceedings of Povolzhsky region. Physical and mathematical sciences] – 2013. – № 3(27) – P. 159–169. [in Russian]
- Ivinskaya E. Yu. Teoreticheskiye aspekty issledovaniya neravnovesnykh ekonomicheskikh system na osnove modeli garmonicheskogo oscillyatora [Teortical aspects of studying non-equlibrium economic systems based on the model of harmonic oscillator] / E. Yu. Ivinskaya // Teoriya I praktika obshestvennogo razvitiya. Ekonomicheskiye nauki [Theory and practice of public development. Economic sciences] – 2015. – № 21 – P. 57–59. [in Russian]
- Antonovskaya O. G. O vliyanii nasysheniya nelineynosti na resultaty issledovaniya prinuditelnoy sinkhronizatsii metodom priblizhennykh tochechnykh otobrazheniy [On the influence of nonlinearity saturation on the results of the forced synchronization received by means of approximate point mappings method] / O. G. Antonovskaya // Matematicheskoye modelirovaniye I optimalnoye upravleniye. Vestnik NNGU [Mathematical modeling and optimal control. NNGU bulletin] Nizhny Novgorod. – 1999. – № 2(21). – P. 198–208. [in Russian]
- Antonovskaya O. G. Metod tichechnykh otobrazheniy v zadachakh nelineynoy dinamiki [Point mappings method in non-linear dynamics problems] / O. G. Antonovskaya, V. I. Goryunov. – GmbH: LAP Lambert Academic Publishing, 2013. – 140 p. [in Russian]
- Neymark Yu. I. Metod tichechnykh otobrazheniy v teriyi nelineynykh kolebaniy [Point mappings method in non-linear vibrations theory] / Yu. I. Neymark. – M.: Nauka, 1972. – 472 p. [in Russian]
- Neymark Yu. I. Stokhasticheskie I khaoticeskie kolebaniya [Stochastic and chaotic vibrations] / Yu. I. Neymark, P. S. Landa. – M.: Nauka, 1987. – 424 p. [in Russian]
- Sharkovsky A. N. Sosushestvovaniye ctsiklov nepreryvnogo preobrazovaniya pryamoy v sebya [Cycles co-existence of continuous transformation of straight line to itself] / A. N. Sharkovsky // Ukr. Mat.zhurn. [Ukrainian mathematical magazine] – 1964. – V.26. – № 1. – P. 61–71. [in Russian]
- Antonovskaya O. G. O priblizhennom issledovanii blizkogo k tozhdestvennomu tochechnogo otobrazheniya ploskosti v ploskost [On the approximate study of close to identical point mapping plain to plain] / O. G. Antonovskaya // Matematicheskoye modelirovaniye I optimalnoye upravleniye. Vestnik NNGU [Mathematical modeling and optimal control. NNGU bulletin], Nizhny Novgorod. – 2004. – № 1(27). – P. 63–69. [in Russian]
