МЕТОДЫ РЕШЕНИЯ ОПТИМИЗАЦИОННЫХ ЗАДАЧ С МУЛЬТИМОДАЛЬНОЙ ЦЕЛЕВОЙ ФУНКЦИЕЙ

Требухин А.В.¹, Остроух Е.Н.²

¹Магистрант, Донской государственный технический университет, ²Кандидат технических наук, доцент, Донской государственный технический университет

Статья написана при поддержке гранта РФФИ № 16-01-00391 «Разработка комбинированных алгоритмов для решения распределительных и транспортных задач с использованием идеологии искусственных иммунных систем и биоинспирированных алгоритмов»

МЕТОДЫ РЕШЕНИЯ ОПТИМИЗАЦИОННЫХ ЗАДАЧ С МУЛЬТИМОДАЛЬНОЙ ЦЕЛЕВОЙ ФУНКЦИЕЙ

Аннотация

Описываются методы решения и особенности оптимизационных задач с мультимодальной целевой функцией, с использованием биоинспирированных алгоритмов, в частности, основное внимание уделено генетическим и иммунным алгоритмам. Рассматриваются и анализируются основные проблемы, недостатки и преимущества. Предложены конкретные примеры реализации таких алгоритмов, а также блок-схемы к ним. Произведен вычислительный эксперимент с целью проверки работы запрограммированного алгоритма на целевой функции Шуберта.

Ключевые слова: алгоритмы оптимизации, биоинспирированные алгоритмы, иммунная система, генетические алгоритмы, теория клонального отбора.

Trebukhin A.V.¹, Ostroukh E.N.²

¹Student, Don State Technical University, ²PhD in Engineering, Associate professor, Don State Technical University

The article was written with the support of the RFBR grant No. 16-01-00391 "Development of combined algorithms for solving distribution and transport problems using the ideology of artificial immune systems and bioinspiral algorithms"

METHODS FOR SOLVING OF OPTIMIZATION PROBLEMS WITH MULTIMODAL TARGET FUNCTION

Abstract

Methods of solving and singularities of optimization problems with a multimodal objective function are described with the use of bioengineered algorithms, in particular, the main attention is paid to genetic and immune algorithms. The main problems, disadvantages and advantages are examined and analyzed. Specific examples of the implementation of such algorithms, as well as block diagrams to them are proposed. A computational experiment was performed to check the operation of the programmed algorithm on the Schubert target function.

Keywords: optimization algorithms, bioinspired algorithms, immune system, genetic algorithms, clonal selection theory.

Особенности целевой функции, такие как дискретность и мультимодальность, не дают возможности для использования классических методов (метод ветвей и границ, спортивного спуска и другие), поэтому возникает необходимость в использовании альтернативных методов решения оптимизационных задач с мультимодальной целевой функцией. Рассмотрим биоинспирированные алгоритмы как альтернативные методы решения таких задач, в частности генетические и иммунные алгоритмы.

Понятие «биоинспирированные алгоритмы» можно более подробно объяснить, как алгоритмы, вдохновленные процессами живой природы. Иначе говоря, это использование алгоритмов методов оптимизации, основанных на элементах живой природы для моделирования каких-либо явлений и поиска наиболее эффективных решений.

Генетические алгоритмы. Существует такой подкласс биоинспирированных алгоритмов, как генетические алгоритмы. Они имитируют некоторые фундаментальные аспекты эволюционного процесса неодарвинистской теории. Алгоритм проводит одновременно поиск с набором популяций (решений) кандидатов и связывает с ними объективную оценку, как определяющее значение для каждого из них. Затем алгоритм выбирает из полученных значений среди популяций те решения, которые являются наиболее подходящими. Следующее поколение (т.е. новая популяция) состоит из повторов подходящих значений, которые были генетически мутированы и перешли в следующую биологическую фазу: значения переменных были получены таким образом, что они наследовали характеры своих родителей, а также изменялись случайным образом. Размер этой промежуточной популяции в ходе работы алгоритма уменьшается до размера популяции родителей за счет исключения наименее подходящих под определяющее значение решений [1].

Сформулируем один из способов биологической эволюции на примере практической реализации естественным языком программирования:

«Генетический алгоритм»

НАЧАЛО

             Создать начальную популяцию

             Оценить приспособленность каждой особи

             Стоп:= TRUE

             ПОКА Стоп:= TRUE ВЫПОЛНЯТЬ

             НАЧАЛО

Выбрать две особи с высокой пригодностью, согласно критерию приспособленности, из предыдущего поколения;

Скрестить выбранные особи и получить двух потомков;

Каждую особь подвергнуть мутации;

Оценить приспособленности потомков;

Поместить потомков в новое поколение;

             КОНЕЦ

             ЕСЛИ популяция сошлась ТО Стоп:= FALSE

КОНЕЦ

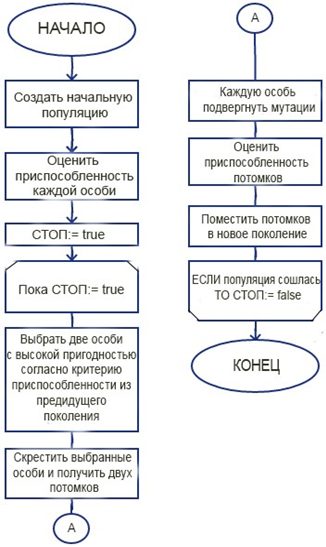
Рис. 1 – Блок-схема генетического алгоритма

Данный метод нахождения оптимального значения, основанный на генетическом алгоритме имеет свои особенности:

-к плюсам можно отнести высокую точность нахождения лучшего решения, которая находится в прямой зависимости от начального размера популяции;

-к минусам следует отнести низкую скорость выполнения эволюционного алгоритма, основываясь на большом размере начальной популяции особей. Это обосновано тем, что в ходе алгоритма выполняется целенаправленный перебор значений, который, в свою очередь, позволяет избежать ухудшения результата, полученного на предыдущих этапах выполнения алгоритма, что уже можно отнести к плюсам этого алгоритма.

Таким образом и основываясь на этом примере можно запрограммировать в общем виде почти любую задачу, решаемую с помощью генетических алгоритмов оптимизации.

Иммунные алгоритмы. Следующим этапом в развитии такого рода алгоритмов стали иммунные алгоритмы. Они основаны на особенностях функционирования иммунной системы. Иммунная система является одной из самых сложных систем организма человека, а также биологической системой способной к «интеллектуальной» обработке информации. Здесь подразумевается использование таких понятий как обучение, память, возможность распознавания и принятия решения в заранее незнакомой системе ситуации [2]. В различных теориях о иммунной системе чужеродные организмы называют антигенами, для уничтожения которых иммунитет вырабатывает специальные клетки – антитела. Способ обнаружения антител заключается в сравнении свойств различных агентов. Сравнение основано на принципе негативной селекции, который заключается в том, что свойства иммунитета отсутствуют в организме, если у агента обнаружены эти свойства, то он чужой. Следующим этапом является клональная селекция. На этом шаге организм начинает вырабатывать антитела максимально похожие на антигены, что представляет собой процесс клонирования и мутации копий антитела в случайных позициях в ходе работы алгоритма искусственной иммунной системы [3].

Рассмотрим иммунный алгоритм для решения задач оптимизации в общем виде:

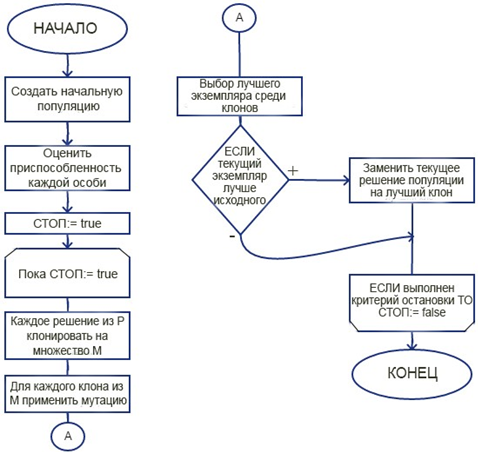
Рис. 2 – Блок-схема иммунного алгоритма

 

«Иммунный алгоритм»

НАЧАЛО

Создать начальную популяцию P

Оценить приспособленность каждой особи

             Стоп:= TRUE

             ПОКА Стоп:= TRUE ВЫПОЛНЯТЬ

             НАЧАЛО

Каждое решение из P клонировать на множество М;

Для каждого клона из М применить мутацию;

Выбор лучшего экземпляра среди клонов;

ЕСЛИ текущий экземпляр лучше исходного ТО

заменить текущее решение популяции на лучший клон;

             КОНЕЦ

             ЕСЛИ выполнен критерий остановки ТО Стоп:= FALSE

КОНЕЦ

Критерием остановки алгоритма обычно является либо достижение лимита по времени, либо достижение лимита по итерациям.

Рассмотренный вид иммунных алгоритмов имеет ряд особенностей, таких как воспроизводство кандидатов методом клональной селекции, разнообразие экземпляров, основываясь на принципе мутации, возможность реализации метода параллельного поиска, что можно отнести к плюсам иммунных методов алгоритмизации.

Результаты численных экспериментов.

Проверим описанный ранее иммунный алгоритм на конкретной целевой функции. Для этого используем двумерную функцию Шуберта:

Для определения максимального значения функции на некотором промежутке был проведен вычислительный эксперимент с использованием иммунного алгоритма. Подготовка к эксперименту состояла в написании программы для вычисления экстремума функции на языке C++ в среде MS Visual Studio. Начальными аргументами функции были выбраны значения «1» и «2», как произвольные. Количество поколений (итераций работы алгоритма) – 1000. Проведенный вычислительный эксперимент показал результат: экстремум функции – 72.5552.

Заключение. Таким образом биоинспирированные алгоритмы являются относительно молодой областью научных интересов в теории оптимизации. У рассмотренных алгоритмов есть свои особенности: достоинства и недостатки, но у них, определенно, есть перспективы для развития и создания более совершенных решений, сочетающих положительные свойства разных видов биоинспирированных алгоритмов.

Список литературы / References

1. Гладков Л.А. Генетические алгоритмы / Л.А. Гладков, В.В. Курейчик, В.М. Курейчик. – М.: Физматлит, 2006. – 320 с.
2. Кушнир Н. В. Искусственные иммунные системы: обзор и современное состояние [Электронный ресурс] / Н. В. Кушнир, А. В. Кушнир, Е. В. Анацкая, П. А. Катышева, К. Г. Устинов // Кубанский государственный технологический университет. – Режим доступа: http://ntk.kubstu.ru/file/714 (дата обращения: 20.05.17).
3. Блюм В. С. Иммунная система и иммунокомпьютинг [Электронный ресурс] / В. С. Блюм, В. П. Заболотский // Санкт-Петербургский институт информатики и автоматизации РАН. – Режим доступа: www.smolensk.ru/user/sgma/MMORPH/N-16-html/blum/blum.pdf (дата обращения: 20.05.17).
4. Барышев А.В., Федотова Е.Л. К вопросу использования надстройки Excel «поиск решения» в задачах линейного программирования [Электронный ресурс]// Интернет-журнал «Науковедение». – 2015. – № 3. URL: http://naukovedenie.ru/PDF/54TVN315.pdf (дата обращения: 22.07.2017)
5. Пантелеев А.В., Мелицкая Д.В. Применение метода искусственных иммунных систем в задачах поиска условного экстремума функций / А.В. Пантелеев, Д.В. Мелицкая // Научный вестник МГТУ ГА. – 2012. – № 184. – С. 54-61.
6. Сергиенко А. Б. Тестовые функции для глобальной оптимизации / А.Б. Сергиенко. – Красноярск: Изд-во СГАУ им. М.Ф. Решетнева, 2015. – 112 с.
7. Остроух Е.Н. Методика контроля информационной безопасности предприятия с использованием адаптационного тестирования/ Е.Н. Остроух, Ю.О. Чернышев, С.А. Мухтаров, Н.Ю. Богданова// Сборник материалов международной научно-практической конференции “Фундаментальные научные исследования: теоретические и практические аспекты”. – Кемерово. – 2016. – т. II. – C. 305-310.
8. Водолазский И. А., Егоров А. С., Краснов А. В. Роевой интеллект и его наиболее распространённые методы реализации // Молодой ученый. – 2017. – №4. – С. 147-153.
9. Сороколетов П.В., Курейчик В.В. Концептуальная модель представления решений в генетических алгоритмах // Известия ЮФУ. Технические науки. №. 9, с. 7-12, 2008.
10. Полупанов A.A., Полупанова Е.Е. Эвристический эволюционно-генетический алгоритм. – М.: Физматлит, 2010. – С. 83-89.

Список литературы на английском языке / References in English

1. Gladkov L.A. Geneticheskie algoritmy [Genetic algorithms] / L.A. Gladkov, V.V. Kurejchik, V.M. Kurejchik. – M.: Fizmatlit, 2006. – 320 p. [in Russian]
2. Kushnir N. V. Iskusstvennye immunnye sistemy: obzor i sovremennoe sostojanie [Artificial immune systems: review and current status] [Electronic resource] / N. V. Kushnir, A. V. Kushnir, E. V. Anackaja, P. A. Katysheva, K. G. Ustinov // Kubanskij gosudarstvennyj tehnologicheskij universitet. – URL: http://ntk.kubstu.ru/file/714 (accessed: 20.05.17). [in Russian]
3. Bljum V. S. Immunnaja sistema i immunokomp'juting [Immune system and immunocomputing] [Electronic resource] / V. S. Bljum, V. P. Zabolotskij // Sankt-Peterburgskij institut informatiki i avtomatizacii RAN. – URL: www.smolensk.ru/user/sgma/MMORPH/N-16-html/blum/blum.pdf (accessed: 20.05.17). [in Russian]
4. Baryshev A.V., Fedotova E.L. K voprosu ispol'zovanija nadstrojki Excel «poisk reshenija» v zadachah linejnogo programmirovanija [On the use of the Excel add-in "search for solutions" in linear programming problems] [Electronic resource]// Internet-zhurnal «Naukovedenie». – 2015. – № 3. URL: http://naukovedenie.ru/PDF/54TVN315.pdf (accessed: 22.07.2017)
5. Panteleev A.V., Melickaja D.V. Primenenie metoda iskusstvennyh immunnyh sistem v zadachah poiska uslovnogo jekstremuma funkcij [Application of the method of artificial immune systems in the search for conditional extremum functions] / A.V. Panteleev, D.V. Melickaja // Nauchnyj vestnik [Scientific herald] MGTU GA. – 2012. – № 184. – P. 54-61.
6. Sergienko A. B. Testovye funkcii dlja global'noj optimizacii [Test functions for global optimization]/ A.B. Sergienko. – Krasnojarsk: Izd-vo SGAU im. M.F. Reshetneva, 2015. – 112 p.
7. Ostrouh E.N. Metodika kontrolja informacionnoj bezopasnosti predprijatija s ispol'zovaniem adaptacionnogo testirovanija/ E.N. Ostrouh, Ju.O. Chernyshev, S.A. Muhtarov, N.Ju. Bogdanova// Sbornik materialov mezhdunarodnoj nauchno-prakticheskoj konferencii “Fundamental'nye nauchnye issledovanija: teoreticheskie i prakticheskie aspekty” [Collection of materials of the international scientific and practical conference "Fundamental scientific research: theoretical and practical aspects"]. – Kemerovo. – 2016. – t. II. – P. 305-310.
8. Vodolazskij I. A., Egorov A. S., Krasnov A. V. Roevoj intellekt i ego naibolee rasprostranjonnye metody realizacii [Roaring intelligence and its most common methods of implementation] // Molodoj uchenyj [Young Scientist]. – 2017. – №4. – P. 147-153.
9. Sorokoletov P.V., Kurejchik V.V. Konceptual'naja model' predstavlenija reshenij v geneticheskih algoritmah [Conceptual model of representation of solutions in genetic algorithms] // Izvestija JUFU. Tehnicheskie nauki. №. 9 [News of SFEDU. Technical science. № 9], p. 7-12, 2008.
10. Polupanov A.A., Polupanova E.E. Jevristicheskij jevoljucionno-geneticheskij algoritm [Heuristic evolutionary-genetic algorithm]. – M.: Fizmatlit, 2010. – P. 83-89.