ГЕОМЕТРИЧЕСКИЕ ФОРМЫ ОБОЛОЧЕК В АРХИТЕКТУРНОМ КОНСТРУИРОВАНИИ

Логунова М.В.¹, Хадидан Мохамед сейф-еддин², Буссаха Фетхи³

¹Профессор, Нижегородский государственный строительный университет, ^2,3аспирант, Нижегородский государственный педагогический университет имени Козьмы Минина – Мининский университет

ГЕОМЕТРИЧЕСКИЕ ФОРМЫ ОБОЛОЧЕК В АРХИТЕКТУРНОМ   КОНСТРУИРОВАНИИ

Аннотация

В течение последнего десятилетия геометрические аспекты архитектуры произвольной формы определили область применения, которая систематически изучается и служит вдохновением для новых математических исследований. В настоящей статье обсуждаются темы, связанные с реализацией оболочек свободной формы различными способами (плоские и изогнутые панели, прямые и изогнутые элементы, кирпичная кладка и т. д.) И освещает взаимосвязь этих вопросов с теорией, в частности дискретную дифференциальную геометрию и дискретную геометрию.

Ключевые слова: сетка, архитектура произвольной формы, круговые структуры, несущая конструкция, статика, расширяемая поверхность, скульптура с изогнутыми складками, вычислительный дизайн.

Lagonova M.V.¹, Hadidan Mohamed Seif-eddine², Boussaha Fethi³

¹Professor of Nizhny Novgorod State University of Civil Engineering, ^2,3postgraduate student, Nizhny Novgorod State Pedagogy university

GEOMETRIC SHAPES OF SHELLS IN ARCHITECTURAL DESIGN

Abstract

During the last decade, the geometric aspects of freeform architecture have defined a field of applications which is systematically explored and which conversely serves as inspiration for new mathematical research. This paper discusses topics relevant to the realization of freeform skins by various means (flat and curved panels, straight and curved members, masonry, etc.) and illuminates the interrelations of those questions with theory, in particular discrete differential geometry and discrete geometry.

Keywords: mesh, freeform architecture, circle packing, support structure, statics, developable surface, curved-crease sculpture, computational design.

1. Введение

Значительная часть математики вдохновлена проблемами, возникающими вне поля ее изучения. В этой статье мы имеем дело с внешним влиянием на математику от довольно маловероятного источника, а именно архитектуры. Нам не интересны более очевидные способы использования математики в современной архитектуре произвольной формы (см. Рисунок 1), которая включает анализ конечных элементов и инструменты для автоматизированного проектирования. Нашей темой является неожиданное взаимодействие геометрии с пространственной декомпозицией архитектуры произвольной формы в балки, панели, кирпичи и другие физические и виртуальные строительные блоки. Как оказалось, математические вопросы, возникающие в этом контексте, оказались очень привлекательными, и мирские объекты строительного строительства, по-видимому, связаны с несколькими хорошо развитыми математическими теориями, в частности с дискретной дифференциальной геометрией.

Отель Yas Marina в Абу-Даби иллюстрирует разложение гладкой оболочки на прямые элементы, которые расположены в виде опорной конструкции без кручения.

 

Рис. 1 – Архитектура свободной формы

 

2. Оболочки свободной формы с плоскими панелями и прямыми лучами

Оболочки свободной формы, реализованные в виде стальных конструкций, обычно изготавливаются из прямых элементов и плоских панелей из-за высокой стоимости изогнутых элементов. Часто плоские панели образуют водонепроницаемую оболочку. Поскольку три точки в пространстве всегда лежат в общей плоскости, но нет четырех общих точек, то, очевидно, гораздо проще использовать треугольные панели вместо четырехглавых. Несмотря на эту трудность, в последнее десятилетие было много исследований по геометрии оболочек свободной формы на основе четырехсторонних панелей. Это связано с тем, что у них есть четкие преимущества перед треугольными - меньше членов на узел, меньше членов на единицу площади поверхности, меньше деталей и более легкая конструкция (см. Рисунок 2). Крыша Zlote Tarasy в Варшаве (слева) сваривается из прямых кусков и соединителей с паукообразными узлами, которые были вырезаны плазмой из толстой пластины.

 

Рис. 2 – Конструкции из стального стекла после треугольной сетки могут легко моделировать желаемую форму оболочки свободной формы за счет высокой сложности узлов

 

2.1. Сетки. Треугольная сетка представляет собой объединение треугольников, которые образуют поверхность, а края треугольников направляют элементы конструкции из стального стекла. Треугольные грани служат в качестве стеклянных панелей. Аналогичным образом определяются квадратные сетки, а также общие сетки без каких-либо ограничений на валентность граней. Мы используем термин «квадратная сетка», чтобы подчеркнуть, что панели плоские.

2.2. Несущие конструкции. Важной концепцией являются так называемые несущие структуры без кручения, связанные с сетками [16, С. 145]. На рисунке 3 показан пример, а именно расположение плоских четырехсторонних панелей вдоль краев квадратной сетки (которая не имеет плоских граней), так что всякий раз, когда четыре ребра встречаются в вершине, четыре вспомогательных квадрата встречаются по прямой линии. Крыша дворца Роберта и Арлин Когод в Смитсоновском американском художественном музее демонстрирует сетку с четырьмя гранями и связанную несущими конструкциями. Линии сетки не плоские - только вид снаружи показывает, что плоские стеклянные панели, которые функционируют как крыша, не подходят друг к другу.

 

Рис. 3 – Физические несущие конструкции без кручения

3. Оболочки свободной формы из изогнутых панелей

Изогнутые балки и панели используются в архитектуре произвольной формы, несмотря на то, что прямые элементы и плоские панели дешевле и проще в обращении. Это связано с художественными причинами и требуемым качеством конечной поверхности: разрывы в первой и второй производных хорошо видны как разрывы и перегибы в линиях отражения. Такие требования известны в автомобильной промышленности, но в архитектуре нет массового производства, а стоимость изготовления изогнутых элементов намного выше. Как правило, нелегко сбалансировать требуемое качество поверхности, сложность формы и бюджет.

Математические понятия, применимые к изогнутым элементам, в основном дифференциально-геометрического характера и часто являются предельными случаями известных в дискретной дифференциальной геометрии понятий. Важную роль играет оптимизация, как дискретная, так и непрерывная. Рассмотрим несколько технологий изготовления:

- Бетон можно вылить в изогнутые опалубки. Это позволяет использовать прямые элементы (рис. 4) или, в меньшем масштабе, резку горячей проволоки. Аппроксимация поверхностей неположительной кривизны Гауса с линейчатыми поверхностями дает легко построенные недоконверсии. Объединение линейчатых поверхностных полос может быть гладкой поверхностью C 1, даже если в решениях имеются изломы (см. Обозначенную область). Этот проект Заха Хадид был предназначен для музея в Кальяри.

- Листовой металл может быть согнут в форме развиваемой поверхности, см. Рисунок 5. Слева на рисунке: внешняя оболочка концертного зала Диснея в Лос-Анджелесе Фрэнка Гери покрыта металлическими листами и состоит из приблизительно разворачиваемых поверхностей. Справа на рисунке: стеклянный навес на Страсбургской железнодорожной станции демонстрирует «холодные согнутые» стеклянные панели.

- Стеклопакеты с двойным изогнутым покрытием. Они изготавливаются методом горячего изгиба с использованием пресс-форм. На больших конструкциях эта техника использовалась только в ситуациях, когда пресс-формы могут использоваться для производства не только одной панели, см. Рис. 6.

- Одноконтурные стеклянные панели могут быть выполнены путем гибки различными способами (см. Рисунок 6). Слева на рисунке: вход в парижское метро на станции Сен-Лазар имеет вращательную симметрию, что позволяет нам изготавливать несколько стеклянных панелей с одной и той же формой. Центр рисунка: символическое изображение формы с контуром панели. Справа на рисунке: 855 панелей, состоящие из фасада Арены Коринфянам в Сан-Паулу, могут быть изготовлены из 61 формы. В частности, цилиндрическое стекло (см. Рис. 7) сравнительно дешево для использования на машинах. Фасад павильонов на первом этаже Эйфелевой башни имеет цилиндрические стеклянные панели и изогнутые балки с прямоугольным поперечным сечением. Вверху справа на рисунке: наилучшее приближение исходной опорной поверхности цилиндрами. Справа на рисунке: поскольку все четыре поверхности каждого луча изготавливаются путем сгибания плоских кусков стальной плиты, они являются разрабатываемыми поверхностями. Они также представляют собой полудискретную опорную структуру

Рис. 4 – Опалубка для бетона

Рис. 5 – Одно изогнутые поверхности

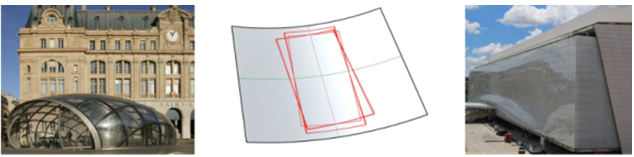
Рис. 6 – Двойные изогнутые панели

Рис. 7 – Панели и балки для павильонов Эйфелевой башни

Вывод. Мы рассмотрели исследования в области математики (дискретная дифференциальная геометрия) и информатики (обработка геометрии), которая либо имеет отношение к свободным формам в архитектуре, либо вдохновлена геометрическими проблемами, которые происходят там.

Эта новая область исследования еще не рассмотрена до конца; она продолжает создавать интересные проблемы и решения. Мы подчеркиваем, что эта область исследования имеет некоторые странные особенности: по художественным соображениям может случиться так, что уникальные решения математических задач на практике неприемлемы. Эта «дизайнерская дилемма» не ограничивается архитектурой.

Исследования, о которых мы сообщали в этой статье, сосредоточены на архитектуре. А в частности, относится к вычислительному дизайну, который лежит в интерфейсе между технологией и искусством. Недавно созданный центр для вычислительного проектирования в Венском технологическом университете нацелен на решение будущих задач в этой широкой области.

Список литературы / References

1. Бальдассини Н. Конструкция изогнутых стеклянных фасадов: павильоны Эйфелевой башни / Н. Бальдассини, Н. Ледюк, А. Шрифтнер. – 2013. – С. 406-410.
2. Бирдон А. Ф. Теорема униформизации для обвязки кругов / А.Ф. Бирдон, К. Стивенсон. – Институт Индиана, 1990. – С.1383-1425.
3. Блок П. Сетевой анализ тяги: новая методология трехмерного равновесия / П. Блок, Дж. Ошендорф. – 2007. – С. 167-173.
4. Бобенко А. Минимальные поверхности от круговых диаграмм: геометрия от комбинаторики / А. Бобенко, Т. Хоффманн, Б. Спрингборн. – 2006. – С. 231-264.
5. Бобенко А. Дискретные и гладкие ортогональные системы: C ∞ -приближение / А. Бобенко, Д. Маттес, Ю. Сурис. – 2003. – С. 2415-2459.
6. Бобенко А. Дискретные изотермические поверхности / А. Бобенко, У. Пинкалл. – 1996. – C. 187-208.
7. Бобенко А. Дискретные поверхности с постоянной отрицательной гауссовой кривизной и уравнение Хироты / А. Бобенко, У. Пинкалл. – 1996. – С. 527-611.
8. Бобенко А. Теория кривизны для дискретных поверхностей на основе параллельности сетки / А. Бобенко, Х. Поттманн, Дж. Валнер – 2010. – С. 1–24.
9. Бобенко А. Вариационные принципы для круговых моделей и теорема Кебе / А. Бобенко, Б. Спрингборн. – 2004. – С. 659-689.
10. Бобенко А. Дискретная дифференциальная геометрия: Интегрируемая структура / А. Бобенко, Ю.В Сурис. – 2009.
11. Карл У. О полудискретных постоянных средних поверхностях кривизны и связанных с ними семействах / У. Карл. – 2016.
12. Карпенков О. О смещениях и кривизнах для дискретных и полудискретных поверхностей / О.Карпенков, Дж. Валнер. – 2014. – С. 207-228.
13. Мюллер К. О дискретных поверхностях постоянной средней кривизны / К. Мюллер // Дискретный компьютер. – 2014. – С. 516-538.
14. Мюллер К. Полудискретные постоянные средние поверхности кривизны / К. Мюллер. – 2015. – C. 459-478.
15. Мюллер К. Ориентированные смешанные области и дискретные минимальные поверхности / К. Мюллер, Дж. Валнер. – 2010.– С. 303-320.
16. Зауэр Р. Дифференценгеометрия / Р. Зауэр // Спрингер. – 1970.

Список литературы на английском языке / References in English

1. Bal'dassini N. Konstrukcija izognutyh stekljannyh fasadov: pavil'ony Jejfelevoj bashni [Construction of bent glass facades: the Eiffel tower pavilions] / N. Bal'dassini, N. Ledjuk, A. Shriftner. – 2013. – P. 406–410.
2. Birdon A.F. Teorema uniformizacii dlja obvjazki krugov. Institut Indiana [Uniformisation law for framing circles. Indiana Institute] / A.F. Birdon, K. Stivenson. – 1990. – P. 1383–1425.
3. Blok P. Setevoj analiz tjagi: novaja metodologija trehmernogo ravnovesija [Thrust network analysis: new methodology for 3D equilibrium] / P. Blok, Dzh. Oshendorf. – 2007. – P. 167–173.
4. Bobenko A. Minimal'nye poverhnosti ot krugovyh diagramm: geometrija ot kombinatoriki [Minimal surfaces from circle diagrams: geometry from combinatorics] / A. Bobenko, T. Hoffmann, B. Springborn. – 2006. – P. 231-264.
5. Bobenko A. Diskretnye i gladkie ortogonal'nye sistemy: C ∞ -priblizhenie [Discrete and smooth orthogonal systems: C ∞ -nearing] / A. Bobenko, D. Mattes, Ju. Suris. – 2003. – P. 2415-2459.
6. Bobenko A. Diskretnye izotermicheskie poverhnosti [Discrete isothermal surfaces] / A. Bobenko, U. Pinkall. – 1996. – P. 187-208.
7. Bobenko A. Diskretnye poverhnosti s postojannoj otricatel'noj gaussovoj kriviznoj i uravnenie Hiroty [Discrete surfaces with constant negative Gaussian curvature and Hirota equation] / A. Bobenko, U. Pinkall. – 1996. – P. 527-611.
8. Bobenko A. Teorija krivizny dlja diskretnyh poverhnostej na osnove parallel'nosti setki [Curvature theory for discrete surfaces based on frame parallelism] / A. Bobenko, H. Pottmann, Dzh. Valner. – 2010. – P. 1-24.
9. Bobenko A. Variacionnye principy dlja krugovyh modelej i teorema Kebe [Variation principles for circle models and Kebe law] / A. Bobenko, B. Springborn. – 2004. – P. 659-689.
10. Bobenko A. Diskretnaja differencial'naja geometrija: Integriruemaja struktura [Discrete differential geometry: Integrated structure] / A. Bobenko, Ju.V. Suris. – 2009.
11. Karl U. O poludiskretnyh postojannyh srednih poverhnostjah krivizny i svjazannyh s nimi semejstvah [On semidiscrete constants of medium surfaces of curvature and their related families] / U. Karl– 2016.
12. Karpenkov O. O smeshhenijah i kriviznah dlja diskretnyh i poludiskretnyh poverhnostej [On shifts and curvatures for discrete and semidiscrete surfaces] / O. Karpenkov, Dzh.Valner– 2014. – P. 207-228.
13. Mjuller K. O diskretnyh poverhnostjah postojannoj srednej krivizny. Diskretnyj komp'juter [On discrete surfaces of constant medium curvature. Discrete computer] / K. Mjuller. – 2014. – P. 516-538.
14. Mjuller K. Poludiskretnye postojannye srednie poverhnosti krivizny [Semidiscrete constant medium surfaces of curvature] / K. Mjuller. – 2015. – P. 459-478.
15. Mjuller K. Orientirovannye smeshannye oblasti i diskretnye minimal'nye poverhnosti [Oriented mixed areas and discrete minimal surfaces] / K. Mjuller, Dzh. Valner. – 2010. – P. 303-320.
16. Zaujer R. Differencengeometrija / R. Zaujer // Springer. – 1970.