РЕЙТИНГ КАК СЛЕДСТВИЕ ПРИНЦИПА МАКСИМУМА ЭНТРОПИИ

Шайдук А.М.¹, Останин С.А.², Семёнов Г.А.³

¹Доктор физико-математических наук, Алтайский государственный медицинский университет, ²Кандидат физико-математических наук, Алтайский государственный университет, ООО "АГФЗ", ³Кандидат физико-математических наук, Санкт-Петербургский государственный аграрный университет

РЕЙТИНГ КАК СЛЕДСТВИЕ ПРИНЦИПА МАКСИМУМА ЭНТРОПИИ

Аннотация

Для математического моделирования сложной социальной системы использованы методы статистической физики. Аналитически доказано, что рейтинг преподавателей учебных заведений определяется принципом максимума энтропии. Нормированные рейтинговые кривые имеют вид распределения Больцмана. По величине отклонения рейтинговой кривой от распределения Больцмана можно количественно оценивать величину управляющего воздействия на элементы системы. Анализ рейтинговой кривой в полулогарифмическом масштабе позволяет обнаружить скрытую структуру системы – определять количество подсистем и их статистические характеристики.

Ключевые слова: рейтинг, управление сложными системами, методы статистической физики.

Shayduk A.M.¹, Ostanin S.A.², Semenov G.A.³

¹PhD in Physics and Mathematics, Altai state medical university, ²PhD in Physics and Mathematics, Altai state university, ³PhD in Physics and Mathematics, Saint-Petersburg state agrarian University

RATING AS A CONSEQUENCE OF MAXIMUM ENTROPY PRINCIPLE

Abstract

For the mathematical modeling of complex social systems used methods of statistical physics. Analytically proved that the rating of teachers of educational institutions is determined by the principle of maximum entropy. Standardized rating curve has the form of the Boltzmann distribution. The magnitude of deviations from the Boltzmann distribution curve rating may be quantified amount of control to the system elements. Analysis of the rating curve in the semi-log scale allows you to discover the hidden structure of the system - to determine the number of subsystems and their statistical characteristics.

Keywords: rating, control of complex systems, methods of statistical physics.

Вариационные ряды часто являются исходным объектом исследования случайных величин методами статистики [1-4]. Естественным образом вариационные ряды получаются при построении различных рейтингов [5-8].

Для целей анализа управляющих воздействий представляют интерес следующие вопросы. Влияют ли процессы управления на вид рейтинговой кривой? Какими процессами определяется вид рейтинговой кривой и можно ли эту кривую получить теоретически?

Основанием для подобных вопросов служит любопытное совпадение. На рисунке 1а приведён безразмерный рейтинг преподавателей одного из университетов, который представляет собой вариационный ряд, упорядоченный по убыванию некоторой характеристики – баллов, количественно характеризующих интеллектуальные ресурсы, созданные преподавателем. А на рисунке 1б представлен безразмерный ранжированный по убыванию значений компонент спектр случайного сигнала (нормального шума). Видно, что эти кривые практически совпадают, хоть и порождаются совершенно различными физическими и социальными процессами.

 

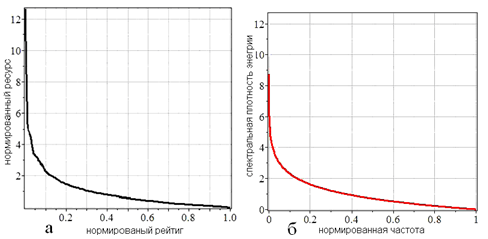
Рис. 1: а – рейтинг профессорско-преподавательского состава Алтайского государственного университета (АлтГУ); б – ранжированный спектр случайного сигнала

 

Попробуем доказать, что это совпадение не случайно. Относительно формирования рейтинга выдвинем следующие, на первый взгляд малоправдоподобные, гипотезы:

1. каждый субъект (преподаватель) с равной вероятностью (не зависящей от его квалификации и других качеств) может генерировать любой итоговый ресурс (получить балл) ;
2. итоговая рейтинговая кривая получается случайно;
3. наблюдаемая рейтинговая кривая является просто наивероятнейшей рейтинговой кривой или близкой к ней.

Оказывается, что перечисленных гипотез достаточно, чтобы получить явный вид рейтинговой кривой. Эта проблема (для функции плотности распределения в термодинамическом равновесии) давно решена в статистической физике (см., например, [9]). Чтобы не загружать читателя необходимостью разбираться с физической терминологией, приведём здесь краткий вывод, адаптированный к рассматриваемой задаче.

Для упрощения вывода разобьем ось непрерывного ресурса  на небольшие интервалы  и пронумеруем их снизу индексом , начиная с единицы. Координату середины интервала номер  обозначим, как . Пусть  – число объектов (преподавателей), обладающих ресурсом (баллами) величиной . В рамках модели формирования рейтинговой кривой считаем, что все объекты с равной вероятностью могут получить ресурс любой величины. Кроме того, должны выполняться условия:

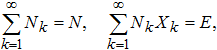  (1)

где N (количество всех объектов) и E (общий ресурс) – постоянные величины. Тогда число способов N объектов распределить по ресурсам (т.е. число возможных рейтинговых кривых) есть

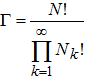  (2)

В соответствии с принятой гипотезой, наблюдаться будет та рейтинговая кривая, которая встречается чаще всего, т.е. соответствует максимуму функции (2). Обычно удобно искать не максимум функции , а максимум энтропии

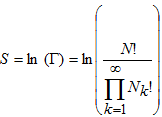  (3)

по переменным N_k. Упростим выражение (3), используя приближение Стирлинга  [9], справедливое при N»1 :

  (4)

Для определения максимума энтропии (4) при дополнительных условиях (1) воспользуемся методом множителей Лагранжа [8], с помощью которого задача поиска условного экстремума сводится к поиску безусловного экстремума вспомогательной функции. Введем вспомогательную функцию

  (5)

где β и γ – множители Лагранжа. Условие максимума запишем как

  (6)

Решением системы уравнений (6) будет совокупность функций   (7)

в которой неизвестные постоянные определяются из условий (1). Соотношение (7) и определяет число объектов N_k, обладающих ресурсом Χ_k. Число объектов, ресурс которых больше некоторого произвольно выбранного значения Х, можно определить из распределения ресурсов по объектам (7):

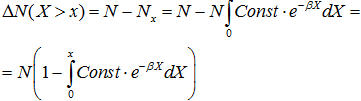  (8)

После вычисления интеграла (8) и нормировки получаем зависимость безразмерного ресурса от относительного рейтинга, показанную на рисунке 2 (гладкая линия).

Сходство теоретически полученного рейтинга и рейтинга профессорско-преподавательского состава АлтГУ подтверждает положенное в основу статистической модели предположение о случайном характере получения объектом некоторого ресурса. Напомним, что переход от дискретных значений к непрерывным и переход от сумм к интегралам возможен только при достаточно больших N. При небольших N не выполняется приближенное равенство (4), и для этого случая необходимо выполнить отдельный расчет. Численность преподавателей АлтГУ составляет около 1000 человек. Как видно из рис. 2, этого достаточно для того, чтобы можно было воспользоваться приближением Стирлинга и приближением (4).

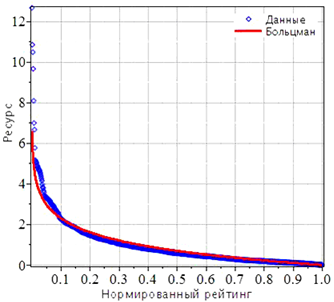
Рис. 2 - Рейтинг профессорско-преподавательского состава АлтГУ () и теоретически рассчитанный рейтинг (гладкая линия)

 

Проведенный анализ показывает, что кривая рейтинга профессорско-преподавательского состава АлтГУ определяется принципом максимального хаоса (энтропии). Вид рейтинговой кривой, в безразмерных координатах, может быть предсказан заранее. Можно заранее предсказать долю преподавателей, набравших баллы выше среднего, баллы в пять раз выше среднего и т.д. Можно заранее предсказать размер финансовых средств, предусмотренных на стимулирование так называемых «высоких» результатов. Наблюдаемое наличие незначительного управляющего воздействия (оно отражено несовпадением кривых) стимулирует лучших и демотивирует отстающих, то есть, направлено в сторону усугубления неравенства.

На рисунке 3 представлен рейтинг преподавателей другого учебного заведения – Ростовского государственного экономического университета (РГЭУ). Из сравнения рисунков 2 и 3 видно, что управляющие воздействия на преподавателей РГЭУ значительно меньше, чем на преподавателей АлтГУ. Перечисленные выше гипотезы, являющиеся содержательной основой математической модели, еще лучше подтверждаются реальными данными РГЭУ. Вероятно, в РГЭУ энтропия достигла своего максимума.

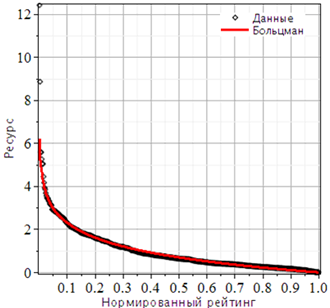
Рис. 3 - Рейтинг преподавателей Ростовского государственного экономического университета (http://www.psysocwork.ru/fileadmin/docs/nestiraemaja/NRPSPBGIPSR.xls)

 

Описанная выше модель включает в себя предположение о том, что каждый участник с равной вероятностью может обладать любым ресурсом  в пределах области определения этого ресурса. Эта гипотеза, естественная для молекулярного движения, кажется странной для субъектов, обладающих собственными целями и способностью к их достижению. Более разумной представляется гипотеза о том, что сознательное поведение людей влияет на распределение ресурсов (в данном случае баллов) между ними. Например, можно предположить, что люди стремятся к обладанию некоторым средним уровнем ресурса, и если субъект имеет значение ресурса ниже среднего, он предпримет меры к увеличению ресурса (тем более в случае баллов, когда ресурс не требуется отбирать у другого субъекта).

Если принять эту последнюю гипотезу, то плотность статистического распределения числа людей по значениям ресурса  должна иметь максимум в районе среднего значения ресурсов. Для численного анализа возможности этой гипотезы будем использовать нормальное распределение

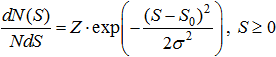  (9)

В качестве среднего значения S₀ и стандартного отклонения σ примем их численные значения, полученные из реального рейтинга. Разумеется, нормировочный множитель Z необходимо вычислить заново, поскольку в данном случае распределение имеет смысл лишь при положительных S.

Однако, использование соотношения (9) приводит к качественно иному поведению рейтинговой кривой, существенно отличающемуся от наблюдаемой и принципиально отличающемуся от гипотезы о равновероятном распределении. На рисунке 4а приведены результаты численного моделирования рейтинговой кривой для распределения типа (9). Наблюдается существенное различие между наблюдаемыми рейтингами (рисунки 2, 3) и результатами моделирования. Причём различие носит и очевидный качественный характер, теперь субъекты, занявшие далеко не первые места в рейтинге, получили ресурсы, большие по сравнению с равновероятным распределением ресурсов.

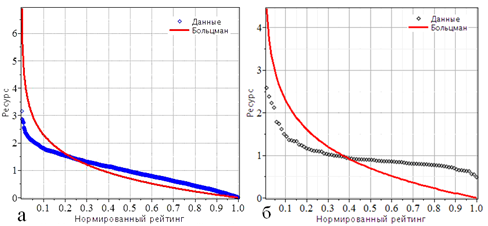
Рис. 4 - Рейтинг субъектов: а – при нормальном распределении ресурсов () и равновероятном распределении ресурсов (гладкая линия); б – уровень денежных доходов населения в целом по России и по субъектам Российской федерации за 2014 год (http://www.gks.ru/wps)

 

Это отчётливо видно из рисунка 5б, где приведена разность между модельным рейтингом типа (9) и рейтингом при равновероятном распределении ресурсов. Теперь победители получили значительно меньшие ресурсы, а проигравшие – значительно большие. Рейтинг подобного вида показан на рисунке 4б (уровень доходов населения по России и по субъектам Российской федерации).

Таким образом, гипотеза о том, что субъекты учебных организаций предпринимали действия, приводящие к увеличению их ресурса, если он оказывался малым, не подтверждается численным моделированием. Численное моделирование в этом случае приводит к результатам, качественно отличающимся от наблюдаемых экспериментально. Гипотеза о хаотическом распределении баллов приводит к гораздо более точному совпадению с экспериментом.

Обратимся теперь к попыткам объяснить некоторое небольшое различие между экспериментом и моделью хаотического распределения ресурсов, которое все же наблюдается и не имеет случайной статистической природы. Это различие прослеживается на рисунке 5а, и имеет качественно другое поведение по сравнению с аналогичным графиком 5б. В реальном рейтинге профессорско-преподавательского состава АлтГУ победители обладают большим ресурсом, а проигравшие – меньшим по сравнению с хаотической моделью.

 

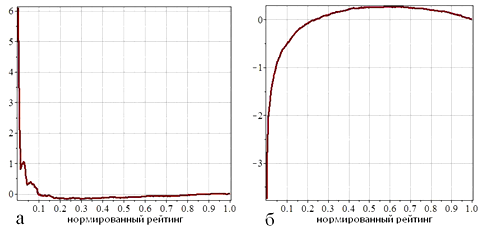
Рис. 5 - Разности рейтингов: а – профессорско-преподавательского состава АлтГУ и теоретического (типа Больцмана); б – модельного рейтинга типа (9) и рейтингом при равновероятном распределении ресурсов

 

Для объяснения подобного поведения рейтинговой кривой сделаем предположение, что совокупность субъектов состоит на самом деле из двух различных множеств, в каждом из которых работает хаотическая модель распределения, но которые отличаются средним значением ресурса (в своем множестве). В статистической физике это соответствует системе, состоящей из двух подсистем с разными температурами. Предположим, что эти два множества не обмениваются ресурсами, хоть и находятся в одной совокупности. Есть много причин появления таких множеств с разным доступом к ресурсам, например, начальники – подчиненные, национальность один – национальность два, мужчины – женщины, старослужащие – призывники и т.д. Тогда для хаотической модели плотность статистического распределения по ресурсу S есть линейная комбинация нормированных распределений Больцмана.

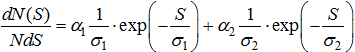  (10)

причем из условия нормировки .

Неизвестные параметры в распределении (10) можно найти из наблюдаемой зависимости ресурса от рейтинга. Действительно, нормированный рейтинг зависит от ресурса :

Неизвестные параметры в распределении (10) можно найти из наблюдаемой зависимости ресурса от рейтинга. Действительно, нормированный рейтинг r зависит от ресурса S:

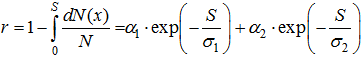  (11)

и, фитируя экспериментальную зависимость соотношением (11), можно определить неизвестные параметры . Однако, прямое применение процедуры фитирования к экспериментальным данным приводит к большой погрешности из-за малого количества точек в области больших ресурсов S. Поэтому оценим эти параметры другим способом.

Предположим, что рейтинги с малым ресурсом формируются в основном одним множеством, а рейтинги с большим ресурсом другим множеством. Математически это означает, что в соотношении (11) при малых значениях рейтинга () основным будет (например) первое слагаемое, а при  – второе слагаемое. В этом случае график зависимости  от S должен (как видно из 11)) иметь характерный излом. Именно это мы и наблюдаем на рисунке 6.

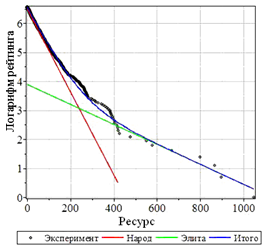
Рис. 6 - Зависимость логарифма рейтинга от ресурса

Следовательно, гипотеза о том, что рассматриваемое множество на самом деле состоит из двух подмножеств с разным доступом к ресурсам (или с разными возможностями генерации ресурса), неплохо согласуется с наблюдаемыми результатами. Из приведённых данных можно оценить и параметры этих подмножеств. Простые вычисления дают .

Следовательно, первое подмножество состоит из (примерно) 650 человек, среднее значение ресурса у которых равно 70. Второе подмножество содержит примерно 50 человек, среднее значение ресурса у этого подмножества равно 290.

Второе подмножество, составляя всего лишь 7% численности, владеет (в рассматриваемом примере генерирует) 32% общего ресурса.

Итак, вид рейтинга учебных заведений определяется, в основном, принципом максимума энтропии. При этом нормированная рейтинговая кривая описывается экспоненциальной функцией типа распределения Больцмана. Отклонение рейтинговой кривой от распределения Больцмана количественно характеризует управляющие воздействия на элементы системы. Анализ рейтинговой кривой в полулогарифмическом масштабе позволяет обнаружить скрытую структуру системы состоящей из большого количества элементов и определить статистические характеристики подсистем.

Литература

1. Хацкевич В.Л. Об экстремальных свойствах средних характеристик вариационных рядов / Вестник Воронежского государственного университета. Серия: Системный анализ и информационные технологии. 2014. № 3. С. 17-24.
2. Рудько И.М. Статистические свойства суммы членов усеченного вариационного ряда / Вестник Томского государственного университета. Управление, вычислительная техника и информатика. 2013. № 1 (22). С. 124‑130.
3. Якымив А.Л. Предельная теорема для средних членов вариационного ряда длин циклов случайной подстановки / Теория вероятностей и ее применения. 2009. Т. 54. № 1. С. 63‑79.
4. Шайдук А.М., Останин С.А. Влияние фрактальной размерности сигнала на распределение энергии в его спектре // Журнал радиоэлектроники: электронный журнал. №2. URL: http://jre.cplire.ru/jre/feb16/5/text.pdf
5. Абламейко С.В., Журавков М.А., Самохвал В.В., Хухлындина Л.М. Новые рейтинги вузов стран-участниц СНГ: корреляция с итогами вебометрического рейтинга / Высшее образование в России. 2014. № 7. С. 11‑22.
6. Мелешкин М.И. О перспективах вхождения российских университетов в первую сотню ведущих университетов мира по рейтингу Times Higher Education / Экономический анализ: теория и практика. 2014. № 19 (368). С. 56‑62.
7. Ефремова В.Н. Экспертные рейтинги как инструменты оценки деятельности глав регионов (на примере рейтингов эффективности губернаторов) / Политическая наука. 2015. № 3. С. 112‑124.
8. Кислицына О.А. Новый подход к измерению качества жизни - индекс социального прогресса: место России в мировом рейтинге / Проблемы современной экономики. 2015. № 3 (55). С. 126‑129.
9. Румер Ю.Б, Рывкин М.Ш. Термодинамика, статистическая физика и кинетика / М.: Наука. 1972. 400 с.

References

1. Hackevich V.L. Ob jekstremal'nyh svojstvah srednih harakteristik variacionnyh rjadov / Vestnik Voronezhskogo gosudarstvennogo universiteta. Serija: Sistemnyj analiz i informacionnye tehnologii. 2014. № 3. S. 17-24.
2. Rud'ko I.M. Statisticheskie svojstva summy chlenov usechennogo variacionnogo rjada / Vestnik Tomskogo gosudarstvennogo universiteta. Upravlenie, vychislitel'naja tehnika i informatika. 2013. № 1 (22). S. 124 130.
3. Jakymiv A.L. Predel'naja teorema dlja srednih chlenov variacionnogo rjada dlin ciklov sluchajnoj podstanovki / Teorija verojatnostej i ee primenenija. 2009. T. 54. № 1. S. 63 79.
4. Shajduk A.M., Ostanin S.A. Vlijanie fraktal'noj razmernosti signala na raspredelenie jenergii v ego spektre // Zhurnal radiojelektroniki: jelektronnyj zhurnal. 2016. №2. URL: http://jre.cplire.ru/jre/feb16/5/text.pdf
5. Ablamejko S.V., Zhuravkov M.A., Samohval V.V., Huhlyndina L.M. Novye rejtingi vuzov stran-uchastnic SNG: korreljacija s itogami vebometricheskogo rejtinga / Vysshee obrazovanie v Rossii. 2014. № 7. S. 11 22.
6. Meleshkin M.I. O perspektivah vhozhdenija rossijskih universitetov v pervuju sotnju vedushhih universitetov mira po rejtingu Times Higher Education / Jekonomicheskij analiz: teorija i praktika. 2014. № 19 (368). S. 56 62.
7. Efremova V.N. Jekspertnye rejtingi kak instrumenty ocenki dejatel'nosti glav regionov (na primere rejtingov jeffektivnosti gubernatorov) / Politicheskaja nauka. 2015. № 3. S. 112 124.
8. Kislicyna O.A. Novyj podhod k izmereniju kachestva zhizni - indeks social'nogo progressa: mesto Rossii v mirovom rejtinge / Problemy sovremennoj jekonomiki. 2015. № 3 (55). S. 126 129.
9. Rumer Ju.B, Ryvkin M.Sh. Termodinamika, statisticheskaja fizika i kinetika / M.: Nauka. 1972. 400 s.