МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЛИЯНИЯ ЭКОНОМИЧЕСКОЙ СРЕДЫ НА ФАКТОРЫ ПРОИЗВОДСТВА

Кузнецов С.Б.

ORCID: 0000-0002-1825-23, Кандидат физико-математических наук, Российская Академия Народного Хозяйства и Государственной Службы Сибирский Институт Управления

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЛИЯНИЯ ЭКОНОМИЧЕСКОЙ СРЕДЫ НА ФАКТОРЫ ПРОИЗВОДСТВА

Аннотация

Целью исследования является получение уравнения изменения скорости развития возобновляемых факторов производства с учетом влияния экономической среды. Влияние экономической среды обуславливается существующими возможностями ведения бизнеса: бюджетно-налоговая политика, возможности кредитования, уровень конкуренции, доступность и образованность трудовых ресурсов, эмбарго и различные виды санкций. В качестве эмпирического аппарата привлекаются исследования проекта «Ведение бизнеса» (Doing Business). Векторный анализ является основным инструментом исследования. Результатом исследования стал вывод уравнения подобного уравнению Навье-Стокса.

Ключевые слова: инвестиции, факторы производства.

Kuznetsov S.B.

ORCID: 0000-0002-1825-23, PhD in Physics and Mathematics, RANEPA Siberian Institute of Management

MODELING OF THE INFLUENCE OF THE ECONOMIC ENVIRONMENT FOR FACTORS OF PRODUCTION

Abstract

The aim of the study is to obtain equations of change of speed of development of renewable factors of production taking into account the influence of the economic environment. The impact of the economic environment is determined by existing business opportunities. This is fiscal policy, lending opportunities, competition level, availability workforce, embargoes, and various types of sanctions. Empirical studies are based on data from the project "Doing business". Vector analysis is used as a mathematical apparatus. The result of this research is the derivation of equation which is similar to the Navier-Stokes equation.

Keywords: investments, factors of production.

Рассмотрим влияние экономической среды на развитие факторов производства. На уровне национальной экономики такое влияние оказывают: изменение уровня налогов, антимонопольное законодательство, конкуренция, возможности кредитования, регистрация и ликвидация предприятий, доступность трудовых ресурсов, постановления правительства, направленные на сдерживание или развитие факторов производства, например, в борьбе с циклическими проявлениями в экономике.

На межнациональном уровне влияние определяется: таможенным законодательством, миграционной политикой государств, уровнем международной торговли, ограничениями в привлечении иностранных капиталов, рабочей силы, различными видами эмбарго и т. п.

Одним из вариантов варьирования колебаниями, возникающими в результате сопротивления среды, осуществляется с помощью инвестиций, кроме того сопротивление экономической среды может повлиять на частоту и амплитуду этих колебаний.

Рассмотрим пространство определяемое временем t, физическим капиталом K, объемом трудовых ресурсов L и человеческим капиталом Н. Классическое уравнение изменения физического капитала имеет вид: , инвестиции предполагаются чистыми. Инвестиции вкладываются не только физический капитал, но и трудовые ресурсы, и человеческий капитал.

Для некоторой «идеальной» экономики имеют место равенства , . Классическое уравнение чистых валовых инвестиций в неоклассической модели роста для факторов производства   имеет вид , где . Скорость изменения инвестиций . Дифференцируя обе части полученного равенства  получаем  равенство .

Предположим, что величина , или, переходя к пределу . Полученная величина определяет относительную скорость прироста валового продукта и представляет собой производную от некоторой кумулятивной предельной производительность экономики. Маленькие значения указывают на стагнацию экономики, а отрицательные значения показывают на явления регрессии.

Из утверждения, доказанного в работе [1, с. 79-80], имеем равенство для любого возобновляемого фактора производства p:

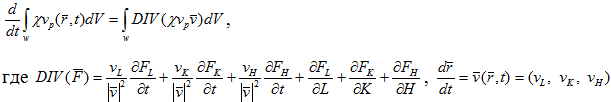
Изменение факторов производства обусловлено скоростью освоения инвестиций в каждый момент времени, т.е. внутри всего объема факторов и сопротивлением экономической среды, с которыми, в первую очередь, сталкиваются вновь появляющиеся факторы «расположенные» на границе изменяющегося объема. В работе [1, с. 179-180] было показано:

где  – тензор сопротивления развитию факторов производства.

Из утверждения, доказанного в работе [2, с. 41-42] получим равенство:

Тензор должен зависеть от скорости факторов производства и показывать темп изменения факторов, т. е., другими словами, выражаться через производные от скорости по факторам производства  размерность которых и соответствует темпу и от самой скорости с некоторым коэффициентом, обладающим размерностью. При небольшом изменении факторов производства скорость развития не может быть большой, поэтому в тензоре можно взять только первые производные. Зависимость σ_pl от  считаем линейной, это достигается разложением ряд Тейлора и отбрасыванием малых величин. Факторы производства у нас равноправные, т. е. вид тензора должен быть симметричный относительно производных  и скорости. В предположение постоянной скорости от времени, но зависящей от факторов производства, получим отсутствие завихрения, и тензор представляет собой диагональную матрицу, зависящую от скорости развития возобновляемых факторов производства, и поэтому, не зависящие от значений  и  члены должны отсутствовать в тензоре σ_pl. Всем перечисленным требованиям удовлетворяет выражение:

где η — динамический коэффициент ведения бизнеса, отражающий связь развития факторов производства с инвестициями. Коэффициент не зависит от скорости, и не имеет размерность. Вспомогательный коэффициент θ имеет размерность (единица времени)/(денежная единица в квадрате).

Распишем подробно динамическую дивергенцию    (1) где .

Уравнений (1) представляет собой наиболее общий вид одного из векторных уравнений, которое описывает развитие экономики с учетом сопротивления экономической среды. Рассмотрим частный случай :  и возьмем коэффициент .

После преобразования, получим общий вид системы уравнений развития экономики с учетом сопротивления экономической среды с постоянным коэффициентом ведения бизнеса:

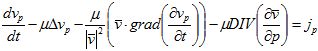  (2)

где p некоторый фактор производства  — оператор Лапласа;  — коэффициент экономического состояния среды, в общем случае зависит от времени.

Система дифференциальных уравнений (2) представляет собой разновидность уравнения Навье–Стокса и при малых значениях μ является уравнением чистых валовых инвестиций в модели роста. Доказательство существования решения классического уравнения Навье–Стокса вошло в число самых сложных математических проблем XXI столетия [3]. Задача является некорректной, и одним из способов преодоления трудностей является учет малого «шума» и случайных процессов, происходящих в экономике. Но на современном этапе анализа экономических явлений такое усложнение задачи может привести к отрицательному результату.

Сопротивление экономической среды характеризуется коэффициентом ведения бизнеса η. Одними из возможных вариантов определения η могут быть процентили, или относительные значения рейтинга ведения бизнеса. Определение рейтинга стран можно осуществить, опираясь на проект «Ведение бизнеса» (Doing Business) [4]. Отношение рейтинга страны к общему количеству стран назовем легкостью ведения бизнеса, а коэффициент ведения бизнеса η является функцией от этого отношения. В таблице указаны страны с самым высоким и низким уровнем легкости ведения бизнеса и ряд европейских стран (табл. 1).

Таблица 1 - Легкость ведения бизнеса

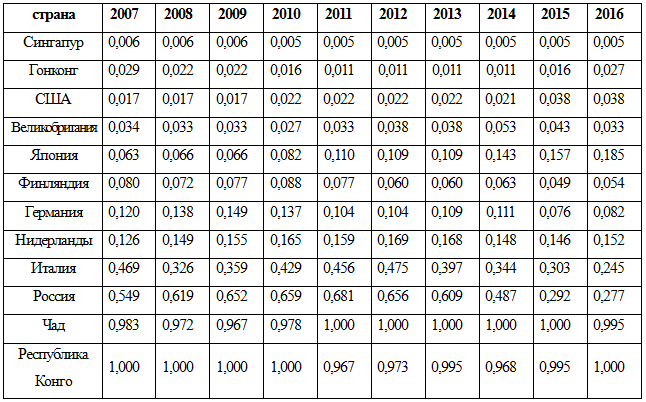
Сингапур является лидирующей страной на протяжении всех лет исследования, рейтинг замыкают Чад и Республика Конго. Россия твердо занимала середину таблицы, но последние два года передвинулась вверх. Япония в последние годы сдает позиции и перемещается в низ. Большинство европейских стран показывают стабильность с небольшими флуктуациями.

Коэффициент ведения бизнеса должен быть возрастающей функцией от значения легкости ведения бизнеса, так как с более низким местом в рейтинге сопротивление экономической среды увеличивается.

Вычисление реального сопротивления экономической среды в настоящее время возможно только эмпирически с использованием уравнения (2) и знания реальных объемов инвестиций вложенных в фактор производства, и результатов этих вложений.

Литература

1. Кузнецов С. Б. Динамика обновления факторов производства. Новосибирск: ЦПИ: Изд-во СИБПРИНТ, 2010. с. 26-32.
2. Кузнецов С.Б. Моделирование поведения экономических показателей. // Вестник Челябинского государственного университета. – 2011. - №16. – с. 41-43.
3. Ладыженская О. А. Шестая проблема тысячелетия: уравнения Навье–Стокса, существование и гладкость//Успехи мат. наук. – 2003. – Т.58, № 2. – С. 45–78.
4. World development report 2006-2016 (Doing business) [Электронный ресурс]. URL: http://www. russian. doingbusiness. org/ (Дата обращения06.2016).

References

1. Kuznecov S.B. Dinamika obnovlenija faktorov proizvodstva. - Novosibirsk: Sibprint, - 2010, - 312 p.
2. Kuznecov S.B. Modelirovanie povedeniya ehkonomicheskih pokazatelej. // Vestnik CHelyabinskogo gosudarstvennogo universiteta 2011. - №16. – s. 41-43.
3. Ladyzhenskaya O. A. SHestaya problema tysyacheletiya: uravneniya Nav'e–Stoksa, sushchestvovanie i gladkost' // Uspekhi mat. nauk. – – T. 58, № 2. – S. 45–78.
4. World development report 2006-2016 (Doing business) [EHlektronnyj resurs]. URL: http://www. russian. doingbusiness. org/ (Data obrashcheniya 05.06.2016).