КОРРЕЛЯЦИОННЫЙ МЕТОД ОБРАБОТКИ ЭЛЕКТРОКАРДИОСИГНАЛА ДЛЯ ПОСТРОЕНИЯ УСТРОЙСТВА АНАЛИЗА АРИТМИЙ
Горохов С.Н.1, Галимзянов Э.Р.2
1ORCID:0000-0001-6152-9483, Кандидат технических наук, доцент, 2Старший преподаватель, Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ
КОРРЕЛЯЦИОННЫЙ МЕТОД ОБРАБОТКИ ЭЛЕКТРОКАРДИОСИГНАЛА ДЛЯ ПОСТРОЕНИЯ УСТРОЙСТВА АНАЛИЗА АРИТМИЙ
Аннотация
В статье рассмотрен корреляционный метод обработки электрокардиосигнала (ЭКС) для определения аритмий по первому стандартному отведению, необходимый для построения устройства – портативного анализатора аритмий. Обработка заключается в поиске и анализе формы зубцов электрокардиосигнала с использованием математической модели электрической активности сердца. Кроме того, разработанный метод позволяет вычислить длительности QRS-комплекса исходя из определенной на реальном сигнале длительности R-зубца, с использованием уравнений линейной регрессии.
Ключевые слова: электрокардиосигнал, математическая модель ЭКС, корреляционный анализ, устройство анализа аритмий.Gorohov S.N.1, Galimzyanov E.R.2
1ORCID:0000-0001-6152-9483, PhD in Engineering, assosiate professor, 2Senior Lecturer, Kazan National Research Technical University named after A.N.Tupolev - KAI
CORRELATION METHOD OF ELECTROCARDIOSIGNAL PROCESSING FOR BUILDING OF ARRHYTHMIA ANALYZER
Abstract
The article proposes a correlation method of electrocardiosignal (ECS) processing for diagnosing arrhythmias by the first standard lead required for building a portable arrhythmia analyzer. The device searches and analyzes the shape of electrocardiosignal peaks using the mathematical model of the cardiac electrical activity. In addition, this method allows calculating the length of the QRS-complex based on the R-peak length determined based on the actual signal by using linear regression equations.
Keywords: electrocardiosignal, mathematical cardiosignal model, correlation analysis, arrhythmia analysis device.Во многих странах, в том числи и в России, большое количество людей страдает от сердечно-сосудистых заболеваний, в связи с чем, актуальной становится разработка эффективных методов диагностики состояния сердца, особенно методов анализа аритмий сердца, так как аритмии не только являются маркерами более серьезных сердечных заболеваний, но и сами могут носить жизнеугрожающий характер.
Развитие радиотехнических систем позволяет создавать недорогие современные медико-диагностические приборы, позволяющие в автоматическом режиме, с высокой степенью достоверности распознавать аритмии сердца, а использование блоков беспроводной передачи данных позволит проектировать сети удаленного наблюдения за пациентами.
В применяемых в настоящее время анализаторах аритмий для определения информационных параметров используется II-е стандартное отведение. Это связано с тем, что проекция вектора ЭДС сердца на данное отведение имеет большую амплитуду и меньшие индивидуальные особенности. Однако в портативных приборах использование II-го стандартного отведения (левая нога – правая рука) затрудняет оперативный съем сигнала по сравнению с I-м стандартным отведением (левая рука – правая рука), которое является ортогональным с II-м. Поэтому использовать стандартные методы и алгоритмы анализа ЭКС для задачи определения аритмий по I-му стандартному отведению не представляется возможным.
Для выделения более слабых сигналов сложной формы в радиотехнических системах широко применяются корреляционные методы и алгоритмы [2]. В настоящее время они уже многократно используются и применительно к ЭКС. Основной сложностью для применения корреляционных методов в электрокардиографии является определение образов эталонных сигналов.
Одним из путей решения этой проблемы является применение моделей элементов ЭКС, с последующей оценкой их параметров и принятия решения по вычисленным параметрам модели. Среди большого количества математических моделей сигнала электрической активности сердца необходимо выбрать модель, обладающую необходимой адекватностью описания ЭКС и в тоже время достаточной простотой реализации. Например, существуют модели ЭКС для применения, которых необходимо знание физиологических параметров тела человека, которые зачастую неизвестны. Поэтому была выбрана модель электрокардиосигнала, лишенная данного недостатка, но в тоже время адекватно описывающая сигналы электрической активности сердца [1, 3].
Применение указанного подхода требует определение начальных параметров модели, которые могут быть получены путем анализа сигналов открытых кардиографических библиотек с уже известными диагностическими заключениями [5].
Таким образом, предполагается в качестве основного метода анализа ЭКС для задачи анализа аритмий использовать корреляционный метод обнаружения элементов ЭКС и определения их параметров.
В качестве модели элемента ЭКС используется экспоненциальная модель кардиосигнала [1, 4]:
![]() (1)
(1)
где A — амплитуда зубца, μ — временное положение зубца σ1, σ2, — коэффициенты масштаба левого и правого «плеч» зубца соответственно.
Для первоначальной оценки временного положения кардиоцикла μ можно применить существующие методы поиска QRS-комплекса, например на основе анализа амплитудных значений и оценок приращений ЭКС. В указанном методе производится поиск вершины R зубца, как самого мощного и имеющего максимальную крутизну.
В дискретном времени оценку μ и начальных значений σ1 и σ2 получают, используя начальные значения ![]() . Считая шум измерения гауссовым, показатель критерия максимального правдоподобия можно определить, используя описание элемента ЭКС моделью (1), как:
. Считая шум измерения гауссовым, показатель критерия максимального правдоподобия можно определить, используя описание элемента ЭКС моделью (1), как:
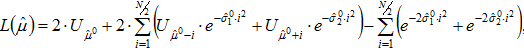 (2)
(2)
где N - интервал анализа.
Первоначально последовательным методом покоординатного спуска определяются параметры R зубца, сначала ![]() , а затем
, а затем ![]() и
и ![]() :
:
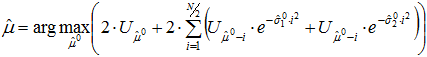 (3)
(3)
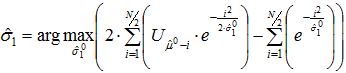 (4)
(4)
![]() (5)
(5)
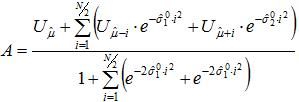 (6)
(6)
Полученные параметры ![]() принимаются за параметры R зубца
принимаются за параметры R зубца ![]() .
.
Далее производится поиск P зубца. Для этого согласно методике изложенной в [1] исходные отсчёты кардиоцикла ЭКС до ![]() пропускаются через цифровой ФНЧ с частотой среза 30 Гц и производится поиск экстремумов полученной последовательности в обратном направлении.
пропускаются через цифровой ФНЧ с частотой среза 30 Гц и производится поиск экстремумов полученной последовательности в обратном направлении.
В качестве стартовой оценки для поиска P зубца берётся временное положение 2-го от R зубца экстремума. Если количество экстремумов менее 2 принимается решение об отсутствии P зубца.
При наличии 2-го экстремума, производится оценка его параметров по аналогии с R зубцом при помощи выражений (2-6) и формируется вектор параметров P зубца ![]() . Если
. Если ![]() лежит в пределах нормы, принимается решение о нормальном типе P зубца, в противном случае принимается решение об искаженном типе Р зубца.
лежит в пределах нормы, принимается решение о нормальном типе P зубца, в противном случае принимается решение об искаженном типе Р зубца.
Интервал P-R определяется как ![]() , где T - период дискретизации ЭКС. R-R интервал определяется как
, где T - период дискретизации ЭКС. R-R интервал определяется как ![]() .
.
Полученные данные собираются в массив по всем кардиоциклам за период наблюдения. Для проверки работоспособности и эффективности разработанной методики был разработан алгоритм математического моделирования.
В качестве исходных данных для алгоритма берутся записи ЭКС по 12 стандартным отведениям из базы [5], для которых уже врачами сделаны заключения о типе аритмий. Из этих записей выбираются только реализации с I-го стандартного отведения. Для каждой из них реализаций проводится анализ согласно предложенной методики и выносится заключение о наличии и типе аритмий. После вынесения заключения оно сравнивается с заранее известным. По результатам сравнения определяется число правильных и ошибочных заключений.
Для автоматического анализа ритма сердца (в частности, для распознавания желудочковых экстрасистол) необходима информация не только о длительностях последовательных RR-интервалов, но и о характере формы QRS-комплексов. Наиболее важно при этом определить, является ли очередной комплекс нормальным или же искаженным, патологическим.
Одним из важных параметров при определении желудочковых аритмий является длительность QRS-комплекса, включающая длительности трёх зубцов Q, R и S. Для определения этого параметра врачами используется второе кардиографическое отведение.
В разрабатываемом приборе анализ кардиосигнала производится по первому стандартному отведению, выделение Q и S зубцов для которого является затруднительным. В тоже время определение длительности R-зубца не вызывает затруднений. Поэтому, нами был предложен метод расчета длительности QRS-комплекса на основе измерения длительности R-зубца. С этой целью была выдвинута гипотеза о линейной зависимости данных параметров. Длительность R-зубца определяется на уровне 0,1. Для этого предлагается с помощью уравнения парной регрессии рассчитать длительность QRS-комплекса на основе длительности R-зубца. В качестве исходных данных были взяты 99 реальных QRS-комплексов из открытой базы ЭКС St.-Petersburg Institute of Cardiological Technics 12-lead Arrhythmia Database [5] .
Для определения параметров уравнения регрессии применяется метод наименьших квадратов, так как он дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии.
В результате вычислений оценок параметров, уравнение регрессии представляет собой следующий вид:
![]() (7)
(7)
где TQRS – длительность QRS-комплеса, TR – длительность R-зубца
При этом анализ качества уравнения регрессии подтвердил адекватность уравнения эмпирическим данным.
Таким образом, предложенный метод обработки электрокардиосигналов, заключающийся в обнаружении и анализе характерных зубцов ЭКС, на основе математической модели, позволяет производить поиск и определять форму P-зубца и QRS-комплекса, а также рассчитывать длительность QRS-комплекса.
Литература
- Абрамов М.В. Аппроксимации экспонентами временного кардиологического ряда на основе ЭКГ // Вестник кибернетики. – Тюмень: Изд-во ИПОС СО РАН – №9 (2010) – с.85-91.
- Вайнштейн Л.А., Зубаков В.Д. Выделение сигналов на фоне случайных помех. Госэнергоиздат, 1960 г. - 448 с.
- Галимзянов Э.Р. Оптимизация метода выделения низкоамплитудных потенциалов с использованием модели электрической активности сердца // Биомедицинская радиоэлектроника. 2012. № 11. С. 49-54.
- Применение экспоненциальной модели электрической активности сердца для анализа электрокардиосигналов./ Э.Р. Галимзянов, С.В. Козлов // Проблемы техники и технологий телекоммуникаций ПТиТТ-2014: материалы XV Международной научно-технической конференции. - Казань. - 2014. - Т.1. - С.68-70.
- PhysioNet [Electronic resource] / St.-Petersburg Institute of Cardiological Technics 12-lead Arrhythmia Database. – URL: http://www.physionet.org/physiobank/database/incartdb/
References
- Abramov M.V. Approximations using exponents of time cardiological series basing on ecg //Cybernetics Bulletin. - Tyumen: Izd-vo IPOS SO RAN – №9 (2010) – p.85-91.
- Vaynshteyn L.A., Zubakov V.D. Vydelenie signalov na fone sluchaynyh pomeh. Gosenergoizdat, 1960 - 448 p.
- Galimzyanov E.R. Optimization of the method for allocation of low-amplitude potentials using heart electrical activities models // Biomedical electronics. 2012. №11. P. 49-54.
- The use of the exponential model of the electrical activity of the heart for electrocardiosignals analysis./ Galimzyanov E.R., Kozlov S.V. // Problemy tehniki i tehnologiy telekommunikaciy PTiTT-2014: materialy XV Mejdunarodnoy nauchno-tehnicheskoy konferencii. - Kazan. - 2014. - T.1. - P.68-70.
- PhysioNet [Electronic resource] / St.-Petersburg Institute of Cardiological Technics 12-lead Arrhythmia Database. – URL: http://www.physionet.org/physiobank/database/incartdb/
