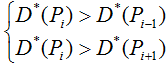ВЕРОЯТНОСТНЫЙ КРИТЕРИЙ СУЩЕСТВОВАНИЯ ПЕРИОДИЧЕСКИХ ТОЧЕЧНЫХ ВСПЛЕСКОВ В ЭМПИРИЧЕСКИХ ДАННЫХ

Томша П.П.

Аспирант, Санкт-Петербургский государственный экономический университет

ВЕРОЯТНОСТНЫЙ КРИТЕРИЙ СУЩЕСТВОВАНИЯ ПЕРИОДИЧЕСКИХ ТОЧЕЧНЫХ ВСПЛЕСКОВ В ЭМПИРИЧЕСКИХ ДАННЫХ

Аннотация

Предложен критерий выявления периодических всплесков в дискретной функции с невозрастающей вогнутой тенденцией. Критерий основан на биномиальном критерии.

Ключевые слова: периодические всплески, функция спроса, критерий наличия, биномиальный критерий, невозрастающая тенденция.

Tomsha P.P.

Postgraduate, St. Petersburg State University of economics

THE PROBABILISTIC CRITERIA OF THE EXISTENCE OF PERIODIC OUTLIERS IN THE EMPIRICAL DATA

Abstract

The criterion of detection of periodic outliers in the discrete function with non-increasing concave trend is suggested. The criterion bases on the binomial test.

Keywords: periodic outliers, demand function, criterion of existence, binomial test, non-increasing tendency.

В качестве модели эластичного по цене спроса в процессе регрессионного анализа, как правило, используются монотонно невозрастающие функции. Однако в некоторых случаях [1, 2] качество моделей можно улучшить, если дополнительно учитывать точечные всплески спроса [3], периодичные по цене.

В данной работе представлен вероятностный критерий выявления в эмпирических данных с вогнутой невозрастающей тенденцией факта наличия таких всплесков, основанный на биномиальном критерии.

Пусть эмпирические данные о величине спроса при разных значениях цены заданы в виде функции с дискретной областью определения . Для простоты далее будем рассматривать случай с постоянным шагом по цене, то есть .

Точка  считается точкой локального максимума эмпирической функции D^*(P), если выполнено:

При построении регрессионной модели эмпирические данные рассматриваются как сумма моделируемой функции D(P)  и случайной ошибки модели ε. Случайная ошибка модели при этом представлена нормально распределенной случайной величиной с математическим ожиданием в точке ноль.

Случайные ошибки в любых трех подряд идущих замеров эмпирических данных можно рассматривать как независимые друг от друга нормально распределенные случайные величины. Вероятность того, что каждая из них будет максимальной из данных трех случайных величин, составляет 1/3.

Вероятность возникновения локального максимума в каждой точке D^*(P_i)  равна произведению вероятностей событий  и – первая разность моделируемой функции D­: .

Таким образом, если вторая разность , то есть модель D(P)  представлена в виде вогнутой функции, вероятность возникновения локального максимума исключительно за счёт случайной ошибки не превышает 1/3.

Предположим, что через точку P^*  из области определения D^*(P)  проходит последовательность периодических всплесков с периодом . Обозначим через V множество всплесков из данной последовательности, находящихся в области определения . Также обозначим через n число всплесков  и через m – число локальных максимумов функции D^*(P) в точках из V.

В случае, если на множестве V  нет периодических всплесков функции D^*(P)  и наличие локальных максимумов в этих точках обуславливается исключительно фактором случайности, можно рассматривать m как случайную величину с биномиальным распределением .

Как было показано ранее, при  вероятность случайного возникновения локального максимума не превышает 1/3. Для таких случаев .

Рассмотрим в качестве H₀ гипотезу о том, что локальные максимумы на точках из V возникли исключительно из-за случайной ошибки . Для проверки гипотезы H₀ воспользуемся биномиальным критерием [4, с. 591] с уровнем значимости α=0.05.

Если биномиальный критерий позволит отвергнуть гипотезу H₀, мы можем говорить о наличии в эмпирических данных последовательности периодических по цене всплесков с периодом T и включающим в себя P^*.

Таким образом, в качестве критерия наличия в эмпирических данных периодических по цене всплесков можно использовать факт существования таких P^* и T, для которых биномиальный критерий не сможет отвергнуть гипотезу о появлении локальных максимумов в соответствующих точках эмпирических данных исключительно из-за случайной ошибки.

Литература

1. Томша П.П. Феномен потребительского выбора в Интернете // Финансовая аналитика: проблемы и решения. – 2013. – №37. – С. 39-42.
2. Томша П.П., Минаков В.Ф., Сотавов А.К. Формирование сервисами интернет-аномалий потребительского выбора / П.П. Томша, В.Ф. Минаков, А.К. Сотавов // Информационные технологии в бизнесе: Сборник научных статей 8‐й Международной научной конференции / Под ред. В.В. Трофимова, В.Ф. Минакова. – Санкт‐Петербург. – 2013. – С. 115–122.
3. Томша П. П. Анализ особенностей ожиданий рынка с помощью преобразования Фурье [Текст] / П. П. Томша // Актуальные направления научных исследований: от теории к практике : материалы III Междунар. науч.–практ. конф. (Чебоксары, 29 янв. 2015 г.) / редкол.: О. Н. Широков [и др.]. – Чебоксары: ЦНС «Интерактив плюс», 2015. – С. 338–339. – ISBN 978-5-906626-59-2.
4. Хальд А. Математическая статистика с техническими приложениями: Пер. с англ. – М.: Издательство иностранной литературы. – 1956. – 664 с.

References

1. Tomsha P.P. Fenomen potrebitel'skogo vybora v Internete // Finansovaja analitika: problemy i reshenija. – 2013. – №37. – S. 39-42.
2. Tomsha P.P., Minakov V.F., Sotavov A.K. Formirovanie servisami internet-anomalij potrebitel'skogo vybora / P.P. Tomsha, V.F. Minakov, A.K. Sotavov // Informacionnye tehnologii v biznese: Sbornik nauchnyh statej 8‐j Mezhdunarodnoj nauchnoj konferencii / Pod red. V. Trofimova, V.F. Minakova. – Sankt‐Peterburg. – 2013. – S. 115–122.
3. Tomsha P. P. Analiz osobennostej ozhidanij rynka s pomoshh'ju preobrazovanija Fur'e [Tekst] / P. P. Tomsha // Aktual'nye napravlenija nauchnyh issledovanij: ot teorii k praktike : materialy III Mezhdunar. nauch.–prakt. konf. (Cheboksary, 29 janv. 2015 g.) / redkol.: O. N. Shirokov [i dr.]. – Cheboksary: CNS «Interaktiv pljus», 2015. – S. 338–339. – ISBN 978-5-906626-59-2.
4. Hal'd A. Matematicheskaja statistika s tehnicheskimi prilozhenijami: Per. s angl. – M.: Izdatel'stvo inostrannoj literatury. – 1956. – 664 s.