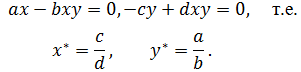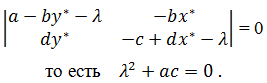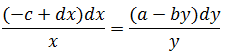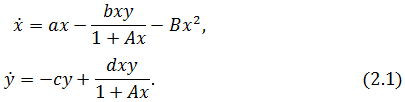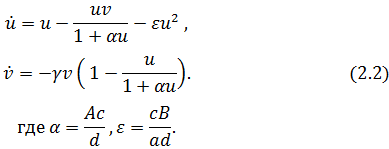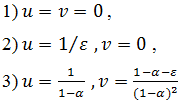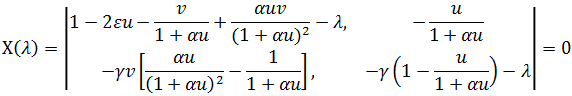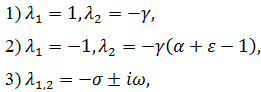МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МЕЖДУНАРОДНОГО РЫНКА ТОВАРА

Гудков А. В.

Преподаватель, Нижегородская государственная консерватория (академия) имени М.И.Глинки, Нижний Новгород

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МЕЖДУНАРОДНОГО РЫНКА ТОВАРА

Аннотация

В статье предложена математическая модель международного рынка товара с учетом динамического баланса между покупателями и продавцами, объемами спроса и предложения, с одной стороны, и поведением рынка, с другой. Данная модель отражает поиск исследования состояния рынка, построения максимально точного прогноза его динамики в среднесрочной и долгосрочной перспективах. Рассматриваются возможные методы внешнего и внутреннего регулирования международного  рынка.

Ключевые слова: международный рынок, равновесие, регулирование рынка, математическая модель рынка.

Gudkov A.V.

 Professor, The Nizhniy Novgorod State Glinka conservatoire (academy), Nizhniy Novgorod

MATHEMATICAL MODEL OF INTERNATIONAL COMMODITY MARKET

Abstract

In the article the mathematical model of the international commodity market with view of taking into account the dynamic balance between buyers and sellers, the volumes of supply and demand and market behavior. This model reflects the search of market's investigation, build the most accurate prediction of its dynamics in the medium and long term. Possible methods of internal and external control of the international market. 

Keywords: international market equilibrium, market regulation, a mathematical model of the market.

В условиях современной российской экономики перед коммерческими организациями все чаще встает перспектива выхода продаваемого на внутрироссийском рынке товара на международный рынок, то есть на ту часть внутригосударственных рынков, которые взаимодействуют с рынками других государств. Понятие "Международный рынок" не следует отождествлять с другим термином: "Мировой рынок", т.к. последний включает в себя так же невзаимодействующую с иностранными рынками часть внутригосударственного рынка. Таким образом, международный рынок является частью мирового.

Необходимость организации вывода продаваемого товара на международный рынок может возникнуть в нескольких экономических ситуациях: во-первых, при локальном "пресыщении" товаром на внутреннем рынке, то есть при прохождении внутрироссийского жизненного цикла товара пикового значения спроса и начала этапа спада продаж. В этом случае выведение товара на международный рынок позволит резко увеличить количество потенциальных покупателей и позволит товару начать новый виток жизненного цикла, увеличив продажи и отсрочив период постоянного нисходящего тренда кривой продаж. Во-вторых, для некоторых категорий товаров выведение на внешний рынок целесообразно начать одновременно с началом продаж на внутреннем рынке. Это позволит точнее определить целевого покупателя и оптимизировать сектор рынка, потенциально захватываемый организацией. Так же фактор успешных продаж на международном рынке часто является катализатором роста спроса на товар на внутрироссийском рынке.

Исходя из этого необходимо подробнейшим образом изучить поведение международного рынка товара. В данной статье будет проведено математическое моделирование рынка абстрактного товара с точки зрения соотношения уровня спроса и предложения. Ценовой фактор в данном исследовании затронут не будет. Это характерно, например, для товара с введенными ограничениями ценового диапазона. Поэтому в простейшем случае рассмотрим две взаимодействующих группы - построим математическую модель покупатель-продавец.

В первой части исследования за основу будет взята гипотеза отсутствия момента пресыщения покупателя товаром. Это характерно на начальных этапах его жизненного цикла.

Итак, предположим, что в вырожденных ситуациях количество покупателей , желающих приобрести товар при практически полном отсутствии его на рынке, растет экспоненциально. То есть:

Так же предположим, что при полном отсутствии покупателей количество продавцов (или, что в данном случае тождественно, объем продаж одного исследуемого продавца)  столь же стремительно сокращается:

Предположим, что продавцы реализуют тем больше товара, чем более многочисленно их количество (или размер реализуемой организацией товара). Таким образом, при наличии хотя бы одного продавца (или минимально возможного объема выведенного на рынок товара):

Объем проданного товара способствует увеличению количества продавцов (или, соответственно, роста объема продаж исследуемого нами продавца) и поэтому:

Дифференциальные уравнения (1.1) и (1.2) – хорошо известные уравнения В.Вольтерры-А.Лотки. Состоянием порожденной этими уравнениями динамической системы являются количества x и y покупателя и продавца, фазовым пространством - октант x ≥ 0, y ≥ 0. Согласно сделанным выше предположениям, при  возрастает по экспоненте, то есть при x = 0 y убывает по экспоненте. Точка x = y = 0 является состоянием неустойчивого равновесия типа "седла" [Ю.Неймарк]. Это следует из того, что вблизи точки равновесия x = y = 0 членами, содержащими произведение малых величин x и y, модно пренебречь и приближенно

Кроме равновесия x = y = 0, возможно, есть еще равновесие x = x*, y = y*, где x* и y* - отличные от нуля решения уравнений

Тип равновесия (x*,y*) можно найти, составляя его характеристическое уравнение

Корни полученного характеристического уравнения являются чисто мнимыми:  и отвечают в линейном приближении состоянию равновесия типа центр, который, при учете отбрасываемых при линеаризации членов, может оказаться как устойчивым, так и неустойчивым фокусом. В данном случае более детальный анализ позволяет обнаружить, что нелинейные члены сохраняют вид состояния равновесия, то есть оно остается типа центра. Этот анализ основывается на возможности интегрирования уравнений Вольтерры-Лотки. Уравнения Вольтерры-Лотки можно записать в виде:

Отсюда, разделив переменные, получим:

и после интегрирования

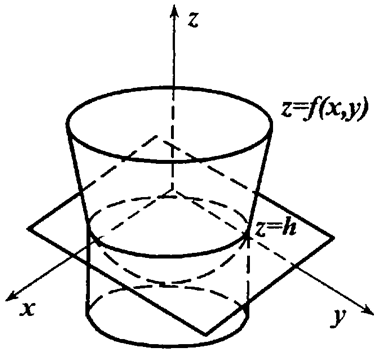
где h - произвольная константа. Полученное уравнение - уравнение фазовых траекторий. Каждой траектории соответствует локализованное значение константы h. Качественно построить фазовые траектории на плоскости x,y можно, заметив, что каждая из этих фазовых траекторий получается путем проектирования на плоскость x,y линии пересечения поверхности

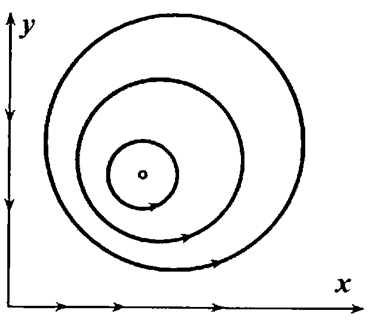
плоскостью z = h (Рис. 1.1). Приблизительный вид этой поверхности, показанный на Рис.1.1 можно найти из соображений, что на осях x и  при возрастании хотя бы одной из переменных x или y. Точке минимума этой поверхности z = f(x,y) отвечает состояние равновесия (x*,y*). Все остальные траектории, как видно из Рис. 1.1 представляют собой концентрические овалы, полностью заключенные друг в друге и охватывающие точку равновесия (x*,y*) таким образом, что фазовый портрет получаем в виде, показанном на Рис. 1.2

Рис. 1.1 - Геометрическое построение фазового портрета модели рынка с экспоненциальным ростом количества потребителей и продавцов.

Согласно полученному фазовому портрету, колебания количеств сторон участников рынка носят периодический характер, но могут проходить с разными "размахами": от практически нулевых до огромных, почти бесконечных в условиях рассматриваемой рыночной ситуации. Но, как отметил исследователь данной модели Вольтерра, временные средние значения количеств покупателей и продавцов x и y остаются неизменными, равными координатам x* и y* состояния равновесия. Это непосредственно следует из усредненных по периоду соотношений

поскольку средние значения их левых частей равны нулю.

Рис 1.2 - Фазовый портрет модели рынка с экспоненциальным ростом количества потребителей и продавцов.

Согласно этой модели, ни изменения параметров a,b,c,d, ни возмущения, приводящие к изменению начальных условий, до тех пор пока y не обращается в нуль, не могут нарушить базовый принцип конкурентного состояния рынка – процесс ориентации его на потребителя, то есть "охоты" продавца за покупателем. Пожалуй, самое благоприятное положение для баланса оптимальных соотношений пары покупатель-продавец международного рынка в данных условиях – находиться вблизи равновесного состояния, поскольку при больших отклонениях происходит слишком значительный размах численности покупателей, впрочем, как и слишком маленького количества продавцов, которое на практике может и вовсе привести к "вырождению" ранка.

Несмотря на кажущуюся простоту, данная математическая модель довольно наглядно и точно характеризует возможные состояния международного рынка с экспоненциальным ростом количества потребителей и продавцов. Это "вырожденный" случай так называемых "экстремальных" условий международного рынка, характерный, например, для выстроенных стратегий ограниченных серий очень ожидаемых на рынке или модных товаров, или довольно точно описывающий рынок в условиях острой нехватки товаров первой необходимости при их ограниченном производстве.

Также данную модель можно интерпретировать как модель международного рынка запрещенных к обороту товаров и международных правоохранительных организаций (в данной модели - переменная ), борющихся за уничтожение оборота данных товаров и поимки продавцов (переменная  в исследованной модели). Исходя из анализа фазового портрета можно сделать вывод, что наиболее эффективные методы борьбы правоохранителей следующие:

1. Прежде всего, если это возможно, международных продавцов незаконного товара следует ликвидировать полностью: оставляя даже очень маленькое их количество, цель искоренения никогда не будет достигнута, т.к. спустя какое-то время, исходя их наличия "пищи" в виде высокого покупательского спроса на запрещенные товары, количество продавцов достигнет, возможно, еще большего значения.
2. Если же полная ликвидация международных продавцов незаконного товара невозможна, то уменьшать их количество целесообразно в некоторой мере и только в верхнем положении относительно равновесного положения фазовой точки, то есть вблизи максимального их количества. Частичная ликвидация при малой численности приведет к еще большему последующему обострению ситуации.

Данная модель при всей своей показательности и простоте имеет ряд существенных недостатков и потому применима лишь в очень ограниченном числе международных рыночных ситуаций. Например, модель становится неудовлетворительной при допущении возможности качественных изменений фазового портрета под влиянием сколь угодно малых изменений правых частей ее дифференциальных уравнений. В экономической практике это означает, что неучет даже самых незначительных факторов может существенно его изменить. Поэтому нет никаких оснований считать данную модель правильной в сколь угодно общем случае, ведь игнорирование второстепенных факторов на практике неизбежно. Такое нежелательное поведение модели Вольтерры-Лотки объясняется тем, что равновесие типа центр, которому отвечают чисто мнимые корни характеристического уравнения, при наличии самых незначительных добавок ?(x,y) и ?(x,y) к правым частям уравнений (1.1) и (1.2) могут смениться на устойчивый или неустойчивый фокус, вокруг которого могут появиться замкнутые устойчивые периодические движения, что существенно изменит фазовый портрет и вытекающие из него поведения продавца и покупателя на международном рынке.

Рассмотрим теперь более сложную рыночную ситуацию: исследуемая математическая модель будет лишена описанного выше недостатка. Она будет учитывать невозможность постоянного неограниченного роста численности продавцов (или размеров исследуемой международной торговой организации) даже при самом благоприятном спросе, а так же ограничения и конкуренцию покупателей за свои потребности и возможности перехода их части на альтернативные товары или иные способы выхода из рассматриваемого сектора международного рынка.  Такая модель будет иметь более сложный вид, а именно:

Она переходит в описанную выше модель Вольтерры-Лотки при A = 0 и B = 0. Введенный параметр A учитывает постепенное уменьшение темпов роста количества продавцов (или размеров исследуемой международной коммерческой организации). Ведь даже при очень большом количестве покупателей, готовых приобретать поставляемый на международный рынок товар, количество продавцов (или размер организации) не может быть большим, чем некоторое b/A, в то же время, как при A = 0 количество продавцов (или размер рассматриваемой организации) могло расширяться неограниченно при x→∞. Параметр B > 0 учитывает ограниченность рынка покупателя, то есть объективную невозможность бесконечного увеличения количества желающих приобрести поставляемый продавцом товар (так же как невозможность неограниченного роста организации, потребляющей поставляемый в любых количествах товар).

Исследование дифференциальных уравнений (2.1) значительно сложнее, чем в модели Вольтерры-Лотки. Его следует начать с уменьшения числа параметров. В (2.1) их шесть. Это количество можно уменьшить до двух, если ввести замену переменных:

Введенная замена переменных приводит дифференциальные уравнения (2.1) к виду:

Как показывает исследование, качественный вид их фазового портрета зависит только от положительных параметров α и ε, тогда как параметр γ на него никак не влияет.

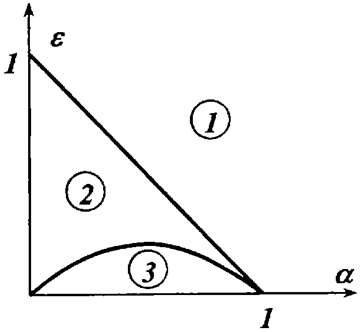
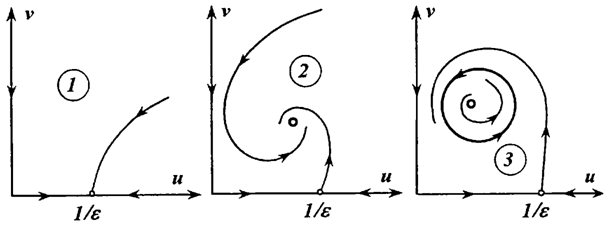
Построение двумерного (переменные ) фазового портрета этих уравнений и бифуркационного портрета распадается на несколько этапов. Сначала находятся и исследуются состояния равновесия. Это исследование подскажет нам возможность автоколебаний. Затем находятся области параметров, отвечающие различным качественным структурам фазового портрета. В результате приходим к бифуркационному портрету Рис. 2.1. Он содержит три области 1, 2 и 3. Каждой из них отвечает свой вид фазового портрета, показанный на рисунке 2.2 с указанием номера области бифуркационного портрета.

Рис. 2.1 - Параметрический портрет уточненной математической модели международного рынка с учетом ограниченного роста объемов спроса и предложения.

Рис. 2.2 - Фазовые портреты уточненной математической модели международного рынка с учетом ограниченного роста объемов спроса и предложения для значений параметров из областей 1,2 и 3 параметрического портрета.

При параметрах из области 1 международный рынок товара вырождается: продавцов не остается, остается минимальное количество покупателей равное u* = 1/ε, отвечающем устойчивому нулевому равновесию фазового портрета 1 на Рис. 1.2.

В области 2 независимое количество покупателей становится неустойчивым и появляется равновесное взаимодействие продавца и покупателя на исследуемом международном рынке.

С переходом параметров в область 3 нарушается равновесное взаимодействие покупателей и продавцов и оно приобретает автоколебательный характер.

Теперь рассмотрим исследование изложенных выше результатов:

Состояния равновесия находятся из уравнений:

Решений три:

Первые два равновесия имеют место при любых положительных α и ε, последнее - только в области 2 и 3, где 1 - α – ε > 0. На границе областей 1 и 2 третье и второе равновесия сливаются.

Для исследования устойчивости найденных равновесий составим характеристическое уравнение:

в которое последовательно подставляем вместо  значения координат равновесий, исследуемых на тип и устойчивость. Для состояний 1,2 и 3 последовательно находим корни этого характеристического уравнения:

где σ обращается в нуль на граничной кривой  областей 2 и 3 (в области 2 - значение  отрицательно, а в области 3 - положительно). В соответствии с теорией бифуркаций при переходе из области 2 в область 3 должно либо рождаться устойчивое периодическое движение от третьего состояния равновесия, либо неустойчивое периодическое движение должно исчезать, влипая в него. Выяснить какой из случаев имеет место в исследуемом примере можно, подсчитав знак так называемой Ляпуновской величины. В данном случае этот процесс приводит к тому, что имеет место рождение неустойчивого периодического движения – автоколебания. В соответствии с этим мы и получили фазовый портрет 3 Рис 2.1.

Исходя из полученных результатов мы можем сделать вывод о поведении международного рынка в описанных условиях с учетом ограниченного роста объемов спроса и предложения. Мы получили три различных варианта развития рыночной ситуации в зависимости от значений описанных выше параметров. В первой, нежелательной как для количества продавцов (или исследуемой организации),  так и для покупателей, ситуации рынок вырождается и остается небольшой непокрытый предложением спрос покупателей на товар. Во второй ситуации имеет место последовательное постоянное движение международной рыночной ситуации к некому строго определенному положению равновесия, при котором на рынке возникает оптимальная ситуация как для покупателей, так и для продавцов - рынок товара сбалансирован. И, наконец, в третьей рыночной ситуации количество продавцов и покупателей последовательно приходит к некоторому постоянному колебанию значений объема приобретаемого на международном рынке товара и количества продавцов вокруг точки оптимального значения рыночного соотношения. Назовем эту ситуацию "нормальные автоколебания рынка". При этом от исследуемой международной торговой организации требуется лишь откликаться на естественные потребности потребителей и их количество будет циклически изменяться то возрастая, то немного снижаясь до некоторого некритического значения.

В заключение отметим, что исследуемая математическая модель при всех попытках ее уточнения является неполной и может быть использована скорее как логически выдержанное описание различных ситуациях, складывающихся на международном  рынке, чем как точный алгоритм подсчета стратегий управления международной коммерческой организацией. Однако она позволяет более точно понять некоторые процессы, происходящие в процессе деятельности международной коммерческой организации в условиях современной экономической ситуации.

Литература

1. Вольтерра В. Математическая теория борьбы за существование. М.: Наука, 1976. – 286 с.
2. Любушин Н.П. Анализ финансового состояния организации. М.: Эксмо, 2007. – 256 с.
3. Неймарк Ю.И. Математические модели в естествознании и технике. Нижний Новгород: ННГУ, 2004. – 401 с.

References

1. Vol'terra V. Matematicheskaja teorija bor'by za sushhestvovanie. M.: Nauka, 1976. – 286 s.
2. Ljubushin N.P. Analiz finansovogo sostojanija organizacii. M.: Jeksmo, 2007. – 256 s.
3. Nejmark Ju.I. Matematicheskie modeli v estestvoznanii i tehnike. Nizhnij Novgorod: NNGU, 2004. – 401 s.