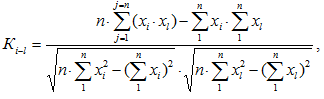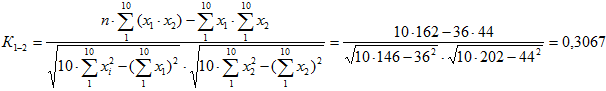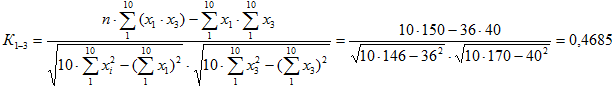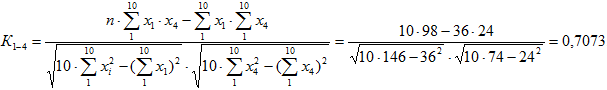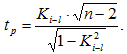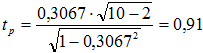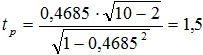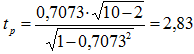ИЗ ПРАКТИКИ КОРРЕЛЯЦИОННОГО АНАЛИЗА В СОЦИОЛОГИЧЕСКИХ ИССЛЕДОВАНИЯХ

Бойко А.Ф.¹, Блинова Т.А.²

¹Доктор технических наук, доцент; ²кандидат технических наук, Белгородский государственный технологический университет им. В.Г. Шухова

ИЗ ПРАКТИКИ КОРРЕЛЯЦИОННОГО АНАЛИЗА В СОЦИОЛОГИЧЕСКИХ ИССЛЕДОВАНИЯХ

Аннотация

В статье представлены результаты исследований применения метода парной корреляции для оценки социологических связей, описан порядок проведения корреляционного анализа с использованием ранговой оценки.

Ключевые слова: метод парной корреляции, коэффициент корреляции, теснота социологической связи.

Boyko A.F.¹, Blinova T.A.²

¹D.Sc. in Engineering, Associate professor; ²Ph.D. in Engineering, Belgorod State Technological University named after V.G. Shukhov

FROM PRACTICE OF THE CORRELATION ANALYSIS IN SOCIOLOGICAL RESEARCHES

Abstract

In article results of researches of application of a method of pair correlation for an estimation of sociological connections are submitted, the order of performance of the correlation analysis with use estimations of a rank.

Keywords: method of pair correlation, factor of correlation, narrowness of sociological connection.

В научно-технических, экономических, социологических исследованиях для установления значимости корреляционных (причинно-следственных) связей между двумя параметрами исследуемого процесса часто используют методы математической статистики. Одним из таких методов является метод измерения тесноты парной корреляционной связи.

Сущность метода заключается в следующем: проводится n опытов, в которых каждый параметр исследуемого процесса получает n независимых значений x_i, где i – номер параметра. Результаты эксперимента подвергаются статистической обработке, в том числе:

• для каждой исследуемой пары параметров определяется коэффициент взаимной корреляции;
• для каждой пары оценивается значимость корреляционной связи по t критерию Стьюдента;
• делается вывод о наиболее существенных парных корреляционных связях и принимаются соответствующие организационно-технические решения.

Необходимо определить тесноту корреляционной связи и ее значимость между несколькими парами людей, оцениваемой по общности морально-этических, интеллектуальных, духовных и социально-политических взглядов.

Так как в такого рода исследованиях прямое, количественное измерение, необходимое для оценки взаимосвязанных параметров невозможно, применяется ранговая оценка по заранее выбранной шкале. Ранжирование носит субъективный характер, поэтому для повышения точности анализа увеличивается количество параллельных опытов (обычно не менее 10). Рассмотрим пример корреляционного анализа, выполненный группой студентов вуза.

Оценка взглядов осуществлялась по пятибалльной шкале путем ранжированного опроса участников. Каждый социологический вопрос представлял собой один опыт. Число вопросов (опытов) n = 10.

1. Как Вы относитесь к бродячим животным?

а) мне их жаль – 5 баллов; б) я к ним равнодушен – 3 балла; в) считаю, их надо уничтожать – 1 балл.

2. Какую музыку Вы любите?

а) классическую – 5 баллов; б) эстрадную – 3 балла; в) к музыке равнодушен – 1 балл.

3. Вы религиозный человек?

а) да – 5 баллов; б) колеблющийся – 3 балла; в) нет – 1 балл.

4. Увлекаетесь ли Вы азартными играми?

а) нет – 5 баллов; б) иногда – 3 балла; в) да – 1 балл.

5. Если Вы оказались свидетелем драки, скандала, что предпримите?

а) пройдете мимо – 1 балл; б) сообщите в милицию – 3 балла; в) вступитесь за пострадавшего – 5 баллов.

6. Как Вы будете вести себя в незнакомой компании?

а) тихо сидеть в уголке – 5 баллов; б) только при необходимости вступать в разговор – 3 балла; в) чувствовать, как у себя дома – 1 балл.

7. Как Вы оцениваете спортивные достижения вуза?

а) все плохо – 1 балл; б) «удовлетворительно» – 3 балла; в) на «отлично» – 5 баллов.

8. Занимаетесь ли Вы спортом, физкультурой?

а) спортом постоянно – 5 баллов; б) физкультурой – 4 балла; в) редко – 3 балла; г) не занимаюсь –1 балл.

9. Есть ли у Вас желание заниматься научными исследованиями?

а) большое желание – 5 баллов; б) иногда возникает – 3 балла; в) никакого желания – 1 балл.

10. Как Вы относитесь к классу богатых людей?

а) безразлично – 5 баллов; б) завидую им – 3 балла; в) отрицательно – 1 балл.

Таким образом, каждый опрашиваемый человек (студент) своим ответом на каждый вопрос оценивается численно: x_i=1…5, где i – порядковый номер студента по списку. Совокупность ответов студента представляет собой статический ряд из переменных параметров x_i.

Общий порядок корреляционного анализа представлен далее.

 

1. Произведен опрос всех студентов группы и результаты (ответы) сведены в одну таблицу 1.

 

Таблица 1 – Результаты опроса

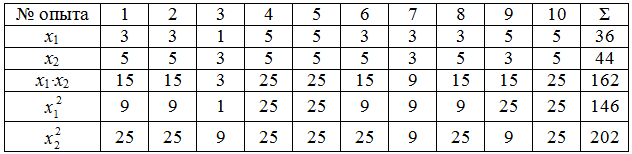
2. Выбраны, начиная с себя (студент 1), еще три последующих по списку студента для установления тесноты социологической связи между студентами в трех парах (табл. 2).

 

Таблица 2 – Результаты опроса студентов

 

3. Определена теснота социологической связи в парах между студентами 1–2, 1–3, 1–4 через коэффициент парной корреляции:

где x_i, x_l – балльные оценки ответов студентов i и l исследуемой пары; К_i-l – коэффициент парной корреляции между этими студентами; j – номер опыта (вопроса).

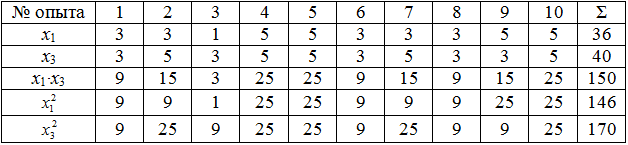
Расчет коэффициентов К_i-l произведен с использованием вспомогательных расчетных таблиц по каждой паре студентов (табл. 3–5).

Таблица 3 – Расчетные данные для пары студентов 1–2

Таблица 4 – Расчетные данные для пары студентов 1–3

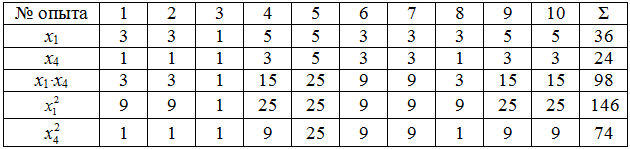
Таблица 5 – Расчетные данные для пары студентов 1-4

Из теории математической статистики известно, что коэффициент корреляции К принимает значения от –1 до +1. Чем больше коэффициент отличается от нуля, тем выше теснота связи. При К =±1 связь между параметрами x_i, x_l  функциональная: при К=+1 – прямопропорциональная; при К=–1 – обратнопропорциональная. При К близким к нулю связи нет. При 0<<1 связь может быть значительной (тесной) или незначительной (случайной). Если К>0, то это говорят о наличии предпосылок для установления близких отношений между двумя людьми; при К<0 ожидаются противоречивые отношения.

Значимость связи оценивается по t – критерию Стьюдента, расчетное значение которого определяется по формуле:

Поэтому для пары 1-2: 

Для пары 1-3: 

Для пары 1-4: 

Полученные расчетные значения t_p сравнивались с табличными t_Т, которые определялись по числу степеней свободы f=n–2=10–2=8 и доверительной вероятности P_д=0,999; 0,99; 0,95; 0,9; 0,8 [1].

Если расчетное значение критерия больше табличного t_p>t_т, то с заданной вероятностью P_д можно утверждать о значимости корреляционной связи. В противном случае (t_p<t_т) связь считается несущественной (случайной).

Для анализа результаты расчетов сведены в таблицу 6.

Таблица 6 – Результаты расчетов

Из расчетов видно, что функциональной социологической связи ни в одной из трех пар нет, так как К≠±1. Наиболее сильная корреляционная связь существует между студентами пары х₁–х₄ (К_1–4=0,7073) и с вероятностью 0,95 можно утверждать о наличии тесной связи между студентами этой пары, так как t_p =2,83>t_т =2,31.

С вероятностью 0,8 можно также утверждать о наличии значительной связи между студентами пары х₁–х₃ (К_1–3=1,5), так как t_p = 1,5>t_т = 1,4, однако вероятность такой связи невысокая (P_д =0,8). Связь между студентами пары х₁–х₂ незначительная (случайная), так как t_p <t_т при любой указанной в таблице доверительной вероятности.

Таким образом, примененный метод парной корреляции позволяет с заданной доверительной вероятностью теоретически определять уровень социологической общности двух людей, а также вероятность формальных предпосылок для установления близких доверительных отношений между ними.

Литература

1. Спиридонов А.А. Планирование эксперимента при исследовании технологических процессов/ А.А. Спиридонов – М.: Машиностроение, 1981. – 184 с.

References

1. Spiridonov A.A. Planirovanie jeksperimenta pri issledovanii tehnologicheskih processov/ A.A. Spiridonov – M.: Mashinostroenie, 1981. – 184 s.