ВОЗМОЖНЫЕ ИЗОСИММЕТРИЙНЫЕ И ДЕФОРМАЦИОННЫЕ МОДИФИКАЦИИ ДЕТЕРМИНИСТИЧЕСКИХ МОДУЛЯРНЫХ СТРУКТУР ИЗ ФРАКТАЛОВ FV, F(IC(1/2)) И F(CM(1/3)) В 2D ПРОСТРАНСТВЕ НА КВАДРАТНОЙ СЕТКЕ

Иванов В.В.

Кандидат химических наук, доцент, Южно-Российский государственный технический университет (Новочеркасский политехнический институт)

ВОЗМОЖНЫЕ ИЗОСИММЕТРИЙНЫЕ И ДЕФОРМАЦИОННЫЕ МОДИФИКАЦИИ ДЕТЕРМИНИСТИЧЕСКИХ МОДУЛЯРНЫХ СТРУКТУР ИЗ ФРАКТАЛОВ FV, F(IC(1/2)) И F(CM(1/3)) В 2D ПРОСТРАНСТВЕ НА КВАДРАТНОЙ СЕТКЕ

Аннотация

Обсуждаются возможные изосимметрийные и деформационные модификации детерминистических модулярных структур из фракталов Вичека FV, канторова множества F(CM(1/3)) и итерационной последовательности точек F(IC(1/2)) в 2D пространстве на квадратной сетке.

Ключевые слова: изосимметрийная модификация, деформационная модификация, модулярная структура. 

Ivanov V.V.

PhD in Chemistry, associate professor, South-Russian state Еngineering University (Novocherkassk Polytechnic Institute)

PROBABLY IZOSYMMETRIC AND DEFORMATIONAL MODIFICATIONS OF DETERMINISTIC MODULAR STRUCTURES FROM FV, F(IC(1/2)) AND F(CM(1/3)) FRACTALS IN 2D SPACE ON SQUARE NET

Abstract

The probably izosymmetric and deformational modifications of deterministic modular structures from next fractals: Vitchec’s fractal FV, Cantor’s multitude F(CM(1/3)) and iterative successive of points F(IC(1/2)) in 2D space on square net were discussed.

Keywords: izosymmetric modification, deformational modification, modular structure.

В соответствии с принципами формирования и модулярного строения фрактальных структур [1, 2] в определенном структурированном пространстве на основе инъективно полученных фракталов Вичека (FV), канторова множества F(CM(1/3)) и итерационной последовательности точек F(IC(1/2)) [3] могут быть сформированы невырожденные модулярные фрактальные структуры. Возможности получения новых фрактальных структур, в частности на основе точечных фракталов IC(1/2) и CM(1/3) в 2D пространстве, могут быть ограничены только специальными требованиями к симметрии и структурным параметрам детерминистических мультифракталов, определенных на квадратной сетке [4]. Представленные в [5-11] методики итерационного модулярного дизайна позволяют сформировать множество детерминистических точечных фрактальных структур с определенными характеристиками. Данные структуры могут послужить условными аппроксимантами (абстракциями) сайт- и сайз-распределений нано- и микрочастиц на поверхности композиционных материалов и покрытий. Анализ возможных деформационных модификаций фрактальных структур существенно дополняют набор их вероятных спектральных характеристик, что может быть использовано при интерпретации некоторых свойств поверхности материалов, в частности при трении и износе [12-14].

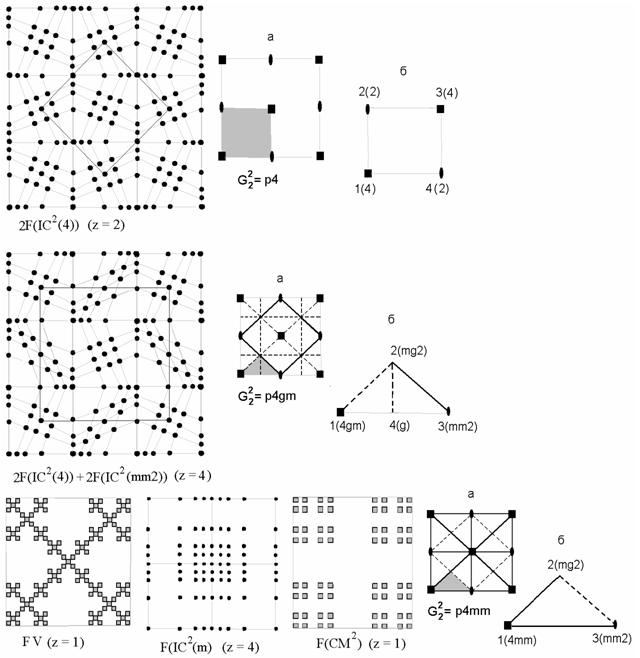
Методом анализа фундаментальной области плоской группы симметрии G²₂ (по аналогии с методикой для точечных групп G³₀ [15-17]) можно перечислить группы симметрии всех возможных симметрийно неэквивалентных разновидностей структуры, которые могут возникнуть в результате ее непрерывных деформаций. Для этого необходимо выделить все структурные элементы области с разной размерностью и локальной симметрией. Соотношения таких структурных элементов плоских групп G²₂ = p4, p4mg и p4mm в соответствующей фундаментальной области для симметричных детерминистических модулярных структур фракталов 2F(IC²(4)), 2F(IC²(4))+2F(IC²(mm2)), а также структур детерминистических фракталов FV, F(IC²(1/2)) и F(CM²(1/3)) представлены на рис.1.

 

Рис.1 – Cимметричные одномодулярные детерминистические фрактальные структуры 2F(IC²(4)), 2F(IC²(4))+2F(IC²(mm2)), структуры детерминистических фракталов FV, F(IC²(1/2)) и F(CM²(1/3)). Обозначения: (а) - схематические изображения симметрии трех плоских групп G²₂, описывающие приведенные фрактальные структуры, (б) - структурные элементы вероятных деформационных модификаций, полученных при анализе фундаментальных областей групп p4, p4mg и p4mm, число z обозначает количество пространственных квадратных ячеек в элементарной ячейке структуры

Результаты анализа вероятных структурных состояний двух плоских групп приведены в таблице 1. Используемые в таблице обозначения структурных элементов фундаментальной области  указаны на рис.1,б.

Таблица 1 - Вероятные структурные состояния детерминистических фрактальных структур на основе фрактала Вичека FV, канторова множества F(CM(1/3)) и итерационной последовательности точек F(IC(1/2))

Установлено, что симметрийные наборы возможных деформационных модификаций структур фракталов FV, F(IC²(1/2)), F(CM²(1/3)) (G²₂ = p4mm) и модулярной структуры 2F(IC²(4))+2F(IC²(mm2)) (G²₂ = p4gm) одинаковы: pmg2, pmm2, pg, pm, p1. Симметрия возможных деформационных модификаций модулярной структуры 2F(IC²(4)) (G²₂ = p4): p2 и p1 (см. табл.1).

 

Литература

1. Иванов В.В., Таланов В.М. Принципы модулярного строения регулярных фрактальных структур // Успехи соврем. естествознания, 2012. - №3. – С.56-57.

2. Иванов В.В. Принципы формирования регулярных простых фрактальных структур // МНИЖ, 2013. - №7. – С. - .

3. Иванов В.В., Таланов В.М. Разбиение структурированного 3D пространства на модулярные ячейки и моделирование невырожденных модулярных структур // Успехи соврем. естествознания, 2012. - №10. – С.78-80.

4. Иванов В.В. Анализ возможности получения новых точечных и квазиточечных фрактальных структур на основе итерационной последовательности и канторова множества точек // Успехи соврем. естествознания, 2013. - №8. – С.129-130.

5. Иванов В.В., Демьян В.В., Таланов В.М. Информация и структура в наномире: модулярный дизайн фрактальных структур в двумерном пространстве // Междунар. журн. эксп. образования, 2010. - №11. - С.153-155.

6. Иванов В.В., Демьян В.В., Таланов В.М. Эволюционная модель формирования и анализ детерминистических фрактальных структур // Успехи соврем. естествознания, 2012. - №4. – С.230-232.

7. Иванов В.В. Общая характеристика возможных гибридных мономодулярных фрактальных структур // Соврем. наукоемкие технологии. 2013.- №.5. – С.29-31.

8. Иванов В.В. Описание и классификация точечных мономодулярных фрактальных структур // Успехи соврем. естествознания, 2013. - №8. – С.134-135.

9. Иванов В.В. Формирование фрактальных структур на основе итерационной последовательности и канторова множества точек с заданными характеристиками в 1D пространстве // Успехи соврем. естествознания, 2013. - №8. – С.136-137.

10. Иванов В.В. Формирование и символьное описание детерминистических гибридных фрактальных структур в 2D пространстве // Соврем. наукоемкие технологии. 2013. - №.9 – С.89-93.

11. Иванов В.В. Детерминистические фракталы на основе итерационной последовательности и канторова множества точек в 2D пространстве // МНИЖ, 2013. - №7. – С. - .

12. Иванов В.В. Комбинаторное моделирование вероятных структур неорганических веществ. – Ростов-на-Дону: Изд-во СКНЦ ВШ, 2003. 204с.

13. Иванов В.В., Щербаков И.Н. Моделирование композиционных никель-фосфорных покрытий с антифрикционными свойствами. - Ростов н/Д: Изд-во журн. «Изв. вузов. Сев.-Кавк. регион», 2008. 112с.

14. Щербаков И.Н., Иванов В.В., Логинов В.Т., и др.. Химическое наноконструирование композиционных материалов и покрытий с антифрикционными свойствами. – Ростов н/Д: Изд-во журн. «Изв. вузов. Сев.-Кавк. регион. Техн. науки», 2011. 132с.

15. Иванов В.В. Вероятные изосимметрийные и деформационные модификации фуллерена С₃₀ // Успехи соврем. естествознания, 2013. - №7. – С.82-84.

16. Иванов В.В. Вероятные изосимметрийные и деформационные модификации фуллерена С₃₆ // Успехи соврем. естествознания, 2013. - №.7 – С.85-87.

17. Иванов В.В. Вероятные изосимметрийные и деформационные модификации фуллерена С₁₈ // Успехи соврем. естествознания, 2013. - №.8 – С.131-133.