ГОМОЛОГИЧЕСКИЕ СООТНОШЕНИЯ И ТОПОЛОГИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ВОЗМОЖНЫХ МОДУЛЯРНЫХ ГИПЕРЯЧЕЕК

Иванов В.В.

Кандидат химических наук, доцент, Южно-Российский государственный технический университет (Новочеркасский политехнический институт)

ГОМОЛОГИЧЕСКИЕ СООТНОШЕНИЯ И ТОПОЛОГИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ВОЗМОЖНЫХ МОДУЛЯРНЫХ ГИПЕРЯЧЕЕК

Аннотация

Обсуждаются некоторые особенности гомологических соотношений и топологических преобразований возможных модулярных гиперячеек, кристаллохимические характеристики гиперполиэдров и варианты их символьных представлений.

Ключевые слова: гомологические соотношения, топологические преобразования, модулярные гиперячейки. 

Ivanov V.V.

PhD in Chemistry, associate professor, South-Russian state Еngineering University (Novocherkassk Polytechnic Institute)

SOME HOMOLOGICAL CORRELATIONS AND TOPOLOGIC TRANSFORMATIONS OF THE POSSIBLE MODULAR HYPER-CELLS

Abstract

Some homological correlations and topologic transformations of the possible modular hyper-cells, crystal chemical characteristics of hyper-polyhedrons and variants of its symbolic presentations were discussed.

Keywords: homological correlations, topologic transformations, modular hyper-cells.

The principle of modular building of nanostructures has been formulated [1]. The problems of the choice of the module for modular design and the algorithm of combinatorial modeling both have been described [2]. The symbolic description of nano-structures by using of information structural codes has been moved [3]. The possible 1D one-periodic and 2D two-periodic nanostructures from polygons with identical topologies and the corresponding plane and volume cyclic and spiral nanostructures by combinatorial modeling method have been designed. The multitudes of the 1D and the 2D base totalities of atoms have been fixed. The brief revue of research papers about crystal chemical peculiarities of the inorganic substances building, the structures of which are includes the designed nanostructures as the structural fragments has been presented [3]. The results of combinatorial modular design of the polygonal nanostructures may be used for modeling of new structural types of 3D crystals, the structures of which are includes polygon-like structural fragments from atoms, 1D and 2D polyhedral modules and modular blocks [3, 4].

A {n}-polygons are the minimal structural elements (2D-cells) of 2D structures (nets), and the various polygons chains are the different nanostructures of 2D E-space. By analogy, the all polyhedrons are the structural elements (3D-cells) of the possible 3D structures, and the various polyhedrons chains and layers are the different nanostructures of 3D E-space. Then the various hyper-polyhedron’s chains, layers and some layer’s packing are the different nanostructures of 4D E-space. The possibility of the presentation of the various variants of nanostructural fragments of the 4D hyperspace was analyzed in this short communication.

It is known the some pairs of the polygonal nanostructures are connected with each other by homological transformations:

Polygons which used for receiving of corresponding homolog are distinguished. The topologic expansion of this polygons {n} is determines the concrete chain of polygonal nets.

By analogy to polygons the homological correlations for some polyhedrons (1) and polyhedral nanostructures (2) are the following:

For receiving of this topological transformations were used the next known correlations [5]:

cub {444} truncated cub {388} cubooctahedron {3434} truncated octahedron {466} octahedron {3333},

and tetrahedron {333} truncated tetrahedron {366} octahedron {3333} truncated dual tetrahedron {366} dual tetrahedron {333}.

Symbolic presentation of the each nano-structural fragment-polyhedron is includes the verbal notation (name) – quantity of vertexes <1, quantity of edges, and faces>, which are intersection in this vertex. The last symbol must be more accurate defined {the all types of faces}. For example, the symbols of some polyhedrons are following:

- tetrahedron {333}, T–4<1,3,3>;

- cub {444}, C–8<1,3,3>;

- octahedron {3333}, O–6<1,4,4>;

- trigonal prism {344}, Tp–6<1,3,3>;

- hexagonal prism {644}, Hp–12<1,3,3>;

- octagonal prism {844}, Op–16<1,3,3>;

- dodecagonal prism {12.44}, Dp–24<1,3,3>;

- hexagonal anti-prism {644}, Hap–12<1,4,4>;

- octagonal anti-prism {844}, Oap–16<1,4,4>;

- dodecagonal anti-prism {12.44}, Dap–24<1,4,4>;

- Laves’s tetrahedron {366} LT–12<1,3,3>.

Then, the chain of topologic transformations from the tetrahedron to dual tetrahedron is the follows:

{333} T–4<1,3,3> {366} LT–12<1,3,3> {3333} O–6<1,4,4> LT^d–12<1,3,3> {366} {333} T^d–4<1,3,3>.

Symbolic presentation of the each nano-structural fragment-hyper-polyhedron is includes the verbal notation (name) – quantity of vertexes <1, quantity of edges, faces, and polyhedrons>, which are intersection in this vertex. The last symbol must be more accurate defined {the all types of polyhedrons}. For example, the symbols of some hyper-polyhedrons are following:

- hyper-tetrahedron {T Tp Tp Tp}, HT–8<1,4,6,4>;

- hyper-cub {C C C C}, HC–16<1,4,6,4>;

- hyper-octahedron {O Tp Tp Tp Tp}, HO–12<1,5,8,5>;

- trigonal hyper-prism {Tp Tp C C}, HTp–12<1,4,6,4>;

- hexagonal hyper-prism {Hp Hp C C}, HHp–24<1,4,6,4>;

- octagonal hyper-prism {Op Tp C C}, HOp–32<1,4,6,4>;

- dodecagonal hyper-prism {Dp Tp C C}, HDp–48<1,4,6,4>;

- hexagonal hyper-anti-prism {Hap Tp Tp Tp Tp}, HHap–24<1,5,8,5>;

- octagonal hyper-anti-prism {Oap Tp Tp Tp Tp}, HOap–32<1,5,8,5>;

- dodecagonal hyper-anti-prism {Dap Tp Tp Tp Tp}, HDap–48<1,5,8,5>;

- Laves’s hyper-tetrahedron {LT Tp Hp Hp}, HLT–24<1,4,6,4>.

And the analogous chain of topologic transformations from the hyper-tetrahedron to dual hyper-tetrahedron is the next:

{T Tp Tp Tp}, HT–8<1,4,6,4> {LT Tp Hp Hp}, HLT–24<1,4,6,4>

{O Tp Tp Tp Tp}, HO–12<1,5,8,5>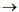 {LT Tp Hp Hp}, HLT^d–24<1,4,6,4> {T Tp Tp Tp}, HT^d–8<1,4,6,4>.

Symbolic presentation of the each nano-structural hyper-layer – hyper-polyhedron’s complex is includes the verbal notation (name) – quantity and topology of all equally vertexes <1, quantity and topology of edges, faces, and polyhedrons>, which are intersection in this vertex. The last symbol must be more accurate defined {the all types of polyhedrons}. For example, the symbols of some layers from hyper-polyhedrons are following:

- hyper-tetrahedron’s layer with tetragon-pyramidal pores

4{T⁴ Tp⁴ Tp⁴ Tp⁴}-4{T Tp Tp Tp}, HT’L–4<1,12,24,16>-4<1,4,6,4>;

- hyper-cube’s layer

4{C⁴ C⁴ C⁴ C⁴}-4{C C C C}, HC’L–4<1,9,20,16>-4<1,4,6,4>;

- the layer from trigonal hyper-prisms

6{Tp⁶ Tp⁶ C⁶ C⁶}-6{Tp Tp C C}, HTp’L–6<1,13,30,24>-6<1,4,6,4>;

- the layer from hexagonal hyper-prisms

3{Hp³ Hp³ C³ C³}-3{Hp Hp C C}, HHp’L–3<1,7,15,12>-3<1,4,6,4>;

- the corrugated layer from Laves’s hyper-tetrahedron with trigon-pyramidal pores

3{LT³ Tp³ Hp³ Hp³}-3{LT Tp Hp Hp}, HLT’L–3<1,7,15,12>-3<1,4,6,4>.

Symbolic presentation of the each nano-structural hyper-layer into 3D space may be used for symbolic presentation of some nano-structural layer’s packing of hyper-polyhedrons. The symbols of 3D hyper-polyhedron’s complex is includes the verbal notation (name) – quantity and topology of all equally vertexes <1, quantity and topology of edges, faces, and polyhedrons>, which are intersection in this vertex. The last symbol must be more accurate defined, too {the all types of hyper-polyhedrons}. For example, the symbols of some layers packing are following:

- a packing of the hyper-tetrahedron’s layers with hyper-octahedron’s pores - 8 HT’LP:

8{T⁸ Tp⁸ Tp⁸ Tp⁸}-8{T Tp Tp Tp}, HT’LP–8<1,24,48,32>-8<1,4,6,4>;

- a packing of the hyper-cube’s layers - 8 HC’LP:

8{C⁸ C⁸ C⁸ C⁸}-8{C C C C}, HC’LP–8<1,18,40,32>-8<1,4,6,4>;

- a packing of the layers of trigonal hyper-prisms – 12 HTp’LP:

12{Tp¹² Tp¹² C¹² C¹²}-12{Tp Tp C C}, HTp’LP–12<1,26,60,48>-12<1,4,6,4>;

- a packing of the layers of hexagonal hyper-prisms – 6 HHp’LP:

6{Hp⁶ Hp⁶ C⁶ C⁶}-6{Hp Hp C C}, HHp’LP–24<1,14,30,24>-24<1,4,6,4>;

- a packing of the corrugated layers of Laves’s hyper-tetrahedrons with bitrigonal-pyramidal pores – 6 HLT’LP:

6{LT⁶ Tp⁶ Hp⁶ Hp⁶}-6{LT Tp Hp Hp}, HLT’LP–6<1,14,30,24>-6<1,4,6,4>.

Several examples of homological correlations and topologic transformations of the 2D nanostructures from polyhedrons and hyper-polyhedrons are the next:

1) topologic transformation from layers of hyper-cubes to its dual analog by splitting edge of cubes or hyper-cubes:

2) topologic transformation between layers of trigonal and hexagonal hyper-prisms by splitting edge of trigonal prisms or hyper-prisms:

3) topologic transformation between layers of trigonal and hexagonal hyper-prisms by splitting edge of hexagonal prisms or hyper-prisms:

4) topologic transformation between layers of complex from trigonal and hexagonal hyper-prisms to layers of hexagonal hyper-prisms by splitting edge of prisms or hyper-prisms:

Several examples of homological correlations and topologic transformations of the 3D structures from polyhedrons and 3D nanostructures from hyper-polyhedrons are the next:

1) topologic transformation from layer’s packing of hyper-cubs to its dual analog by splitting edge of cubs or hyper-cubs:

2) topologic transformation between layer’s packing of trigonal and hexagonal hyper-prisms by splitting edge of trigonal prisms or hyper-prisms:

3) topologic transformation between layer’s packing of trigonal and hexagonal hyper-prisms by splitting edge of hexagonal prisms or hyper-prisms:

4) topologic transformation between layer’s packing of complex from trigonal and hexagonal hyper-prisms to layer’s packing of hexagonal hyper-prisms by splitting edge of prisms or hyper-prisms:

Note, it’s possible, that the various structural anomalous and uniquely peculiarities of crystal chemical building of some organic and inorganic crystals are the result of manifestations in our 3D space of the some structural peculiarities of 4D structures or other hyper-structures with more high dimensions of the topologic space [7-12]. The receiving data about hyper-polyhedrons and its packing into 3D space are necessary for combinatorial modular design of the new chained and layered crystal structures. In particular, the theoretic investigation of crystals with nonstandard stereochemistry, crystal chemistry and uniquely hyper-coordination of atoms is important for receiving of new substances with unusual chemic and physic properties [6, 7, 13-17].

References:

1. Ivanov V.V., Talanov V.M. Principle of Modular Crystal Structure // Crystallography Reports, 2010. T.55. N.3. C.362-376.

2. Ivanov V.V., Talanov V.M. Algorithm of Choice of the Structural Module and Modular Design of Crystals // Russian Journal of Inorganic Chemistry, 2010. T.55. N.6. C.915-924.

3. Ivanov V.V., Talanov V.M. Modular Building of Nanostructures: Information Codes and Combinatorial Design // In Russian journal Nanosistemu: Phizika, Khimia, Matematika, 2010. T.1. N.1. C.72-107.

4. Ivanov V.V., Talanov V.M., Gusarov V.V. Information and Structure in Nano-world: Modular Design of 2D Nanostructures and Fractal Lattices // In Russian journal Nanosistemu: Phizika, Khimia, Matematika, 2011. T.2. N.3. C.121-134.

5. Wells A. Structural inorganic chemistry, Oxford (UK): Clarendon, 1984. Translated under the title Strukturnaya neorganicheskaya khimiya, Moscow: Mir, 1988.

6. Ivanov V.V. Combinatorial Modeling of the Probable Structures of Inorganic Substances. Rostov-on-Don: Northern-Caucasian Science Center of Higher Institute of Learning, 2003.

7. Lord E.E., Mackey А.L., Ranganatan S. Novel geometry for modern materials. Moscow: FIZMATLIT. 2010.

8. Ivanov V.V., Talanov V.M. Symbolic Presentations of Hyper-polyhedra and Transformations of its Geometric Images into 3D Space // Advances in Current Natural Sciences, 2013. № 7. С.74-77.

9. Ivanov V.V., Talanov V.M. Receipt Algorithm of Probable Modular Cells of Crystal Structures from Simplex of 4D Space // Advances in Current Natural Sciences, 2013. № 6. С.61-63.

10. Ivanov V.V., Talanov V.M. Receipt of Probable Modular Cells from Semi-Regular Polytopes of 4D Space with One Intered Vertex of Its Symmetric Projective 3D Images // Advances in Current Natural Sciences, 2013. № 7. С.78-81.

11. Ivanov V.V., Talanov V.M. Receipt Algorithm of Probable Modular Cells of Crystal Structures from Hypercube of 4D Space // Advances in Current Natural Sciences, 2013. № 6. С.64-67.

12. Ivanov V.V., Talanov V.M. Receipt of Probable Fragments of Modular Cells from Hyper-Tetrahedron, Hyper-Octahedron and Trigonal Hyper-Prism of 4D Space // Advances in Current Natural Sciences, 2013. № 6. С.68-72.

13. Ivanov V.V., Balakai V.I., Ivanov A.V., Arzumanova A.V. Synergism in composite electrolytic nickel-boron-fluoroplastic coatings // Rus. J. Appl. Chem., 2006. Т.79. №4. С.610-613.

14. Ivanov V.V., Balakai V.I., Kurnakova N.Yu. et al. Synergetic effect in nickel-teflon composite electrolytic coatings // Rus. J. Appl. Chem., 2008. Т.81. № 12. С.2169-2171.

15. Balakai V.I., Ivanov V.V., Balakai I.V., Arzumanova A.V. Analysis of the phase disorder in electroplated nickel-boron coatings // Rus. J. Appl. Chem., 2009. Т.82. №.5. С.851-856.

16. Bespalova Zh.I., Ivanov V.V., Smirnitskaya I.V., et al. Fabrication of a titanium anode with an active coating based on mixed oxides of base metals // Rus. J. Appl. Chem., 2010. Т.83. N.2. С.242-246.

17. Ivanov V.V., Bespalova Zh.I., Smirnitskaya I.V., et al. Study of the composition of titanium anode with electrocatalytic coat based on cobalt, manganese, and nickel oxides // Rus. J. Appl. Chem., 2010. Т.83. N.5. С.831-834.