МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВОССТАНАВЛИВАЕМОСТИ ПРИРОДНЫХ КОМПЛЕКСОВ ПОСЛЕ ВОЗДЕЙСТВИЯ ПИРОГЕННОГО ФАКТОРА

Буц Ю.В.

Кандидат географических наук, доцент, Харьковский национальный университет имени В.Н. Каразина

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВОССТАНАВЛИВАЕМОСТИ ПРИРОДНЫХ КОМПЛЕКСОВ ПОСЛЕ ВОЗДЕЙСТВИЯ ПИРОГЕННОГО ФАКТОРА

Аннотация

В статье рассматривается анализ существующих математических моделей по влиянию пожаров на природные комплексы. Предложена регрессионная модель, которая учитывает влияние совокупности пирогенных факторов, влияющих на восстановление компонентов природных комплексов после чрезвычайных ситуаций, возникших вследствие природных пожаров.

Ключевые слова: пожар, природный комплекс, математическая модель. 

Buts Yu.V.

PhD of Geography, associate professor, V.N.KarazinKharkivNationalUniversity

MATHEMATICAL MODELING OF RECOVERABILITY OF NATURAL COMPLEXES AFTER INFLUENCE OF FIRE FACTOR

Abstract

The analysis of existent mathematical models that has deal with influence of fires on natural complexes is examined in the article. A regressive model, which takes into account influence of aggregate of progeny factors, that influence on renewal of components of natural complexes after extraordinary situations, arising up because of natural fires, is offered.

Keywords: fire, natural complex, mathematical model.

Одной из основных опасностей для природных комплексов являются пожары (природные пожары). Природный пожар – неконтролируемый процесс горения, стихийно возникающий и распространяющийся в окружающей среде, сопровождается интенсивным выделением тепла, дыма и световым излучением, которое создает опасность для людей и наносит вред объектам хозяйственной деятельности и окружающей среде [8].

В настоящее время научным исследованиям, направленным на изучение влияния пирогенного (дословно - порожденного огнем) фактора на природные комплексы, уделено недостаточно внимания. По большому счету это одиночные экспериментальные исследования влияния огня на определенные компоненты геосистем: растительность, почвы, мезо- и микрофауну, а также прогнозирования и распространения природных пожаров [2].

Вероятно, что всю многовекторную сложность возникновения и распространения пожаров в природных комплексах, возможно решить с помощью математического моделирования. В 80-90-х годах прошлого столетия фундаментальные труды Г.А. Доррера та А.М. Гришина, казалось, в полном объеме обеспечивают математическое моделирование пожаров в природных геосистемах. Однако, как показало время, во-первых, созданные математические модели лишь для лесных биогеоценозов, а во-вторых, стремления сформулировать универсальную математическую модель влияния пожаров на природные комплексы продолжаются до настоящего времени [3, 4].

Как показывает анализ последних публикаций, приоритетными для математического моделирования остаются лесные пожары, несмотря на то, что в последние годы количество других ландшафтно-однородных пожаров существенно увеличилось. А.М. Гришин разделяет такие модели на 4 группы: прогнозирование скорости распространения лесного пожара, контура пожара, хода и тепломассопереноса в зоне и по фронту пожара и общие математические модели, которые прогнозируют то, что и каждая из предыдущих моделей. Он также вводит понятие трех поколений общих математических моделей [3]. Первое поколение моделей рассматривало лес как пористоую дисперсную среду. Процессы конвективного и радиационного теплообмена обеспечивали подогрев, пиролиз и распространение горения сопутствующими горючими материалами. Модели второго поколения дополнительно рассматривали процессы, которые сопровождают лесные пожары – задымленность, конденсацию влаги и возникновение искусственных осадков. Третье поколение моделей учитывало процессы турбулентного тепломассопереноса.

Математические модели, описанные выше, являются сложными для практической реализации из-за значительного количества разнообразных параметров, поэтому, преимущественно, имеют теоретическое значение [7].

Заслуживают внимания научные труды, учитывающие ландшафтно-экологические факторы и состояние геосистем. Среди научных работ, опубликованных в Украине в последние годы, стоит отметить работу А.Я. Калиновского [5], в которой рассмотрена модель распространения ландшафтного пожара с учетом изменчивости параметров ветра и влажности горючего материала на интегральные характеристики низового пожара и показано существенное влияние на форму и размеры контура неоднородного распределения влажности в ландшафте и скорость ветра. Подобные цели преследуются и в работе [6].

Влиянию климатических факторов на процессы развития и прекращения крупных пожаров на открытой местности посвящены исследования [8].

В работе [1] рассматривается связь наличия зеленого травяного покрова в лесу и частоты возникновения очагов лесного пожара, показано, что частоту пожаров в значительной мере определяет наличие и влагосодержания травяного покрова. Обсуждается возможность получения данных о травянистом покрове средствами дистанционного мониторинга.

Модель динамики контура природного пожара под действием совместного влияния ландшафтно-метеорологических факторов предложена А.А. Тарасенко [12]. Итерационная модель динамики контура природного пожара может быть использована для получения прогноза возникновения чрезвычайных ситуаций.

Не смотря на достижения отечественных ученых в моделировании пожаров в природных геосистемах, следует отметить, что на сегодняшний день отсутствуют математические модели, которые бы учитывали индивидуальные особенности природных комплексов. Недостаточно внимания, на наш взгляд, уделяется риску возникновения пожаров в геосистемах разных природных зон. И в конечном итоге, не отображены в отечественной научной литературе исследования направленные на возобновление и восстановление природных комплексов после влияния чрезвычайных ситуаций, в том числе ландшафтных пожаров [2].

Цель данного исследования предполагала построение математической модели, учитывающей влияние совокупности пирогенных факторов, влияющих на восстановление компонентов природных комплексов после чрезвычайных ситуаций, возникших вследствие природных пожаров.

Нами предложено построение регрессионной модели, которая бы учитывала влияние группы факторов (площадь пожаров Y₁, количество пожаров Y₂, потерю гумуса в почве от воздействия огня Y₃, динамику кислотно-щелочного баланса Y₄, и т. д.) на восстанавливаемость геосистем. Результирующим показателем избрана восстанавливаемость видового разнообразия F (видового богатства Маргалефа [10]) растительного покрова ключевых участков, которые подверглись влиянию пирогенного фактора по сравнению с видовым разнообразием (видовым богатством Маргалефа) фоновых участков, не испытывающих действия пожаров (в процентах). Наблюдения проводились в пределах хвойных лесных массивов (сосняков) Харьковского областного управления лесного и охотничьего хозяйства в течение 2008 – 2012 гг.

Соответствующая регрессия является существенно нелинейной, причем по всем факторам прослеживается обратно пропорциональная зависимость.

Нами предложена следующая регрессионная зависимость:

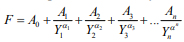, где                                      (1)

F – показатель восстанавливаемости геосистем;

A₁, A₂ ,A₃,…, A_n – неизвестные коэффициенты корреляции;

Y₁, Y₂, Y₃,…,Y_n – факторы, влияющие на возобновление геосистем.

При условии введения новых переменных (факторов) 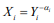регрессия становится линейной:

F = A₀ + A₁X₁ + A₂X₂ + A₂X₂ + …A_nX_n                                         (2)

Для нахождения неизвестных коэффициентов А_і (i = 0….n) использовано метод наименьших квадратов и имеющуюся статистическую информацию по данным Харьковского областного управления лесного и охотничьего хозяйства, а также результаты проведенных экспериментальных исследований на основе полевых наблюдений. Математические расчеты проводились с помощью программы Mathcad.

Вводим прямоугольную матрицу X = { X_ij } (i = 1… n; j = 0… m)

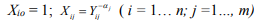
Оператор метода наименьших квадратов позволяет найти вектор оптимальный, с точки зрения метода наименьших квадратов:

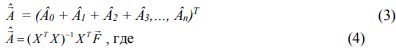
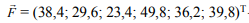– вектор восстанавливаемости (%) по 6 территориальным единицам (лесхозам).

В результате получаем вектор коэффициентов:

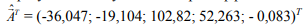
Показатели α_j (j = 1..., n), выбирались из условия минимизации суммы квадратов невязок в заданных точках:

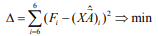                                               (5)

В результате были получены следующие значения:

α₁ = 0,1; α₂  = 0,3; α₃ = 0,2;α₄ = 3;

Соответствующая невязка при этом составила величину ≈ 3%.

Для проверки качества регрессии вычислялся коэффициент детерминации:

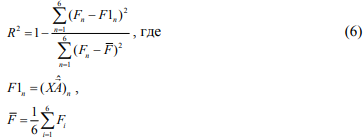
По проведенным расчетам полученное значение составляет R² = 0,993, что свидетельствует об адекватности модели и возможности использования ее для прогнозирования.

Для более наглядного анализа, прогнозирования и расчета доверительных вероятностей, предложены усредненные данные пожаров в геосистемах сосновых лесных массивов Харьковского региона и их последствий. Например, требуется оценить среднюю восстанавливаемость геосистемы при заданных значениях:

- средняя площадь пожара: Y₁₀ = S₀ = 20 га;

- среднее количество пожаров за год: Y₂₀ = N₀ = 30;

- средняя потеря гумуса (%) в почве в результате пожаров: Y₃₀ = Х₀ = 1;

- средняя динамичность кислотно-щелочного показателя рН: Y₄₀ = y₀ = 0,5.

Сделаем точечный прогноз. Предварительно вычислим

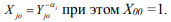
Рассчитаем скалярное произведение, которое и является точечным прогнозом:

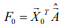                                                    (7)

В данном случае F₀ = 38,45

Введем критерий

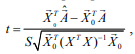где                                              (8)

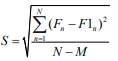– несмещенная оценка среднеквадратичной погрешности аппроксимации. Величина t удовлетворяет t – распределению Стьюдента из N – M степенями свободы. В приведенном случае N = 6 – количество точек наблюдений; M = 5 – количество неизвестных коэффициентов. Учитывая случайный характер оценки, получаем 100 (1–е)% доверительный интервал для математического ожидания прогноза M(F0):

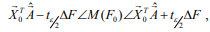где                      (9)

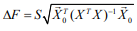– погрешность прогноза.

Учитывая двусторонность критерия 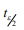– значение критерия Стьюдента, который отвечает 100 (1–е)% доверительный вероятности.

В приведенном примере t_0,025 = 12,706; t_0,05 = 6,314.

Следовательно, можно сделать вывод, что с вероятностью 0,95 математическое ожидание прогнозного значения будет находиться в интервале: 23,49 < M(F₀) < 53,42. Математическое ожидание с вероятностью 0,9 – 31,02 < M(F₀) < 45,89.

Таким образом, анализируя значение коэффициентов 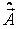, можем сделать вывод, что наибольшее влияние на восстанавливаемость видового разнообразия F (видового богатства Маргалефа) геосистем хвойных (сосновых) лесов в пределах лесостепной зоны Харьковского региона имеют количество пожаров и их периодичность, а также потери гумуса в почвах в результате термического воздействия пирогенного фактора.

Литература

1. Быков В.М. Влияние травяного покрова на природную пожарную опасности в лесу / В.М. Быков, В.А. Комяк, А.Г. Коссе // Проблемы пожарной безопасности. – 2010. – Выпуск 27. – С. 39-44.
2. Гриценко А.В., Буц Ю.В. К вопросу о методологии исследований восстановления геосистем после чрезвычайных ситуаций // Проблеми охорони навколишнього природного середовища та екологічної безпеки: Зб. наук. пр. УкрНДІЕП. – Х.: ВД «Райдер», 2011. – Вип. XXXIІІ. – С.3-11.
3. Гришин А.М. Математическое моделирование лесных пожаров и новые способы борьбы с ними. – Новосибирск: Наука, 1992. – 407 с.
4. Доррер Г. А. Математические модели динамики лесных пожаров. – М.: Лесная пром-сть, 1979. – 160 с.
5. Калиновський А.Я. Влияние изменений параметров ветра и влажности лесного горючего материала на интегральные характеристики низового лесного пожара: дис. канд. техн. наук. – Харьков, 2007. – 150с.
6. Кравців С.Я. Тепловий потік від факелу полум’я лісової низової пожежі з врахуванням його скінченних розмірів і вітру/ С.Я. Кравців, О.П. Сознік // Проблемы пожарной безопасности. – 2010. – Выпуск 27. – С. 118-123
7. Кузик А.Д. Математичне моделювання пожежної небезпеки лісів // Науковий вісник НЛТУ України. – 2011. – Вип. 21 (16). – С. 104-112.
8. Кустов М.В. Влияние травяного покрова на природную пожарную опасности в лесу / М.В. Кустов,В.Д. Калугин, В.В. Коврегин // Проблемы пожарной безопасности. – 2011. – Выпуск 29. – С. 102-109.
9. НАПБ А.01.002-2004 Правила пожежної безпеки в лісах України, затверджені наказом Державного комітету лісового господарства України 27.12.2004 року № 278 зареєстровані в Міністерстві юстиції України 24 березня 2005 року за № 328/10608.
10. Одум Ю. Экология: В 2-х т. Т.2. Пер. с англ. – М.: Мир, 1986. – 376 с.
11. Тарасенко А.А. Модель динамики контура природного пожара под действием совместного влияния ландшафтно-метеорологических факторов // Проблемы пожарной безопасности. – 2008. – Выпуск 24. – С. 194-20.