ИССЛЕДОВАНИЕ ОБЪЕКТОВ МАТЕМАТИЧЕСКОГО АНАЛИЗА С ПРИМЕНЕНИЕМ ЧИСЛЕННЫХ МЕТОДОВ

Богун В.В.

Кандидат педагогических наук, доцент кафедры математического анализа Ярославского государственного педагогического университета им. К.Д. Ушинского

ИССЛЕДОВАНИЕ ОБЪЕКТОВ  МАТЕМАТИЧЕСКОГО АНАЛИЗА С ПРИМЕНЕНИЕМ ЧИСЛЕННЫХ МЕТОДОВ

Аннотация

Рассматривается применение численных методов при решении задач, направленных на исследование определенных объектов математического анализа (числовые последовательности, алгебраические уравнения, интегралы от функций, дифференциальные уравнения). Перечислены численные методы, используемые при решении соответствующих задач, и показана необходимость применения информационных технологий при реализации рассматриваемых вычислительных алгоритмов.

Ключевые слова: объекты математического анализа, численные методы, информационные технологии. 

Bogun V.V.

Ph.D., assistant professor of mathematical analysis of the YaroslavlStatePedagogicalUniversity. KD Ushinsky

RESEARCH FACILITIES MATHEMATICAL ANALYSIS WITH THE APPLICATION OF NUMERICAL METHODS

Abstract

The application of numerical methods for solving tasks designed to study certain objects of mathematical analysis (number sequences, algebraic equations, integrals of functions, differential equations). Lists the numerical methods used in their respective roles, and the necessity of the use of information technology in the implementation of the considered computational algorithms.

Keywords: objects of mathematical analysis, numerical methods, information technologies. 

В рамках математического анализа рассматриваются определенные классы математических объектов с присущими им статическими свойствами (признаки объектов) и динамическими свойствами (действия или операции, совершаемые над объектами). К подобным классам объектов (возможным операциям) можно отнести числовые последовательности (определение пределов числовых последовательностей), алгебраические уравнения (решение алгебраических уравнений), интегралы от функций (нахождение значений определенных интегралов), дифференциальные уравнения (решения дифференциальных уравнений) и так далее.

В определенных случаях реализация указанных операций для рассматриваемых объектов может привести к громоздкости расчетов или невозможности получения необходимых результатов аналитическим путем.

Применение численных методов в подобных случаях позволяет осуществлять решение указанных математических задач с использованием различных оптимизационных алгоритмов поиска значений определенных параметров, которые, зачастую невозможно напрямую рассчитать по готовым формулам в рамках одной итерации.

Исследование объектов математического анализа с применением численных методов [1] подразумевает, как правило, применение нескольких известных вычислительных алгоритмов, результаты расчетов по которым впоследствии сравниваются с целью определения либо более точных значений параметров задачи либо выявления оптимального алгоритма поиска необходимых значений параметров.

Численные методы могут быть использованы при решении следующих задач, направленных на изучение определенных объектов математического анализа [2]:

1. Расчет значений минимальных номеров приближения к пределу числовых последовательностей вида 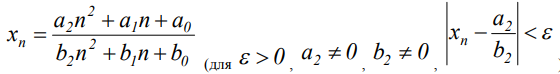  с использованием методов золотой пропорции, Фибоначчи, дихотомии и их сравнительный анализ (числовые последовательности) [3].
2. Приближенные решения алгебраических уравнений с использованием метода дихотомии (бисекции), комбинированного метода хорд и касательных (Ньютона), метода итераций и их сравнительный анализ (алгебраические уравнения).
3. Приближенные вычисления значений определенных интегралов по формулам средних прямоугольников, трапеций, параболических трапеций (Симпсона) и их сравнительный анализ (интегралы от функций).
4. Приближенные решения обыкновенных дифференциальных уравнений первого порядка с использованием методов Эйлера, Рунге-Кутта второго, четвертого порядков точности и их сравнительный анализ (дифференциальные уравнения).

Необходимо отметить, что исследование объектов математического анализа с применением численных расчетных методов целесообразно осуществлять с использованием информационных технологий, позволяющих реализовать определенные алгоритмические структуры на соответствующих языках программирования.

Преимуществами подобного информационного способа решения задач по математическому анализу являются многократность и оперативность выполнения необходимых вычислительных процедур, возможности варьирования значений исходных данных и проведения сравнительного анализа используемых алгоритмов.

Таким образом, при рассмотрении определенных объектов математического анализа с точки зрения статических и динамических свойств применяются численные методы решения соответствующих задач, которые целесообразно реализовывать с применением информационных технологий на программном уровне.

 

Литература

1. Исаков, В.Н. Элементы численных методов [Текст] учеб. пособие для студ. – М.: Академия, 2003. – 192 с.
2. Богун В.В., Смирнов Е.И. Лабораторный практикум по математике с графическим калькулятором [Текст]: учеб. пособие. – Ярославль: Изд-во «Канцлер», 2010. – 272 с.
3. Богун, В.В. Исследование предельных процессов для числовых последовательностей с применением графических калькуляторов [Текст] // Ярославский педагогический вестник. – 2004. – № 4. – C. 179–189.