ИССЛЕДОВАНИЕ РЕЖИМА ТЕМПЕРАТУРЫ АТМОСФЕРНОГО ВОЗДУХА С ПОМОЩЬЮ МОДЕЛИ АВТОРЕГРЕССИИ-СКОЛЬЗЯЩЕГО СРЕДНЕГО

Временная трансформация осредненных значений температуры атмосферного воздуха (годовые, осенние, зимние, весенние и летние) носит сложный характер и является одной из ключевых позиции не только потребностей климатологии, но и нужд народного хозяйства. Такие метеопараметры используются для принятия научно обоснованных решений по адаптацию сельскохозяйственных культур к изменяющимся природно-климатическим условиям. Несмотря на широкое применение временных рядов для анализа и прогнозирования различных метеорологических параметров атмосферы

Этим определяется актуальность детального анализа и прогнозирования временных рядов температуры атмосферного воздуха.

Целью работы является анализ и прогнозирование значений временных рядов метеорологических параметров. Для достижения которой поставлены следующие задачи:

- анализ временного ряда динамики значений средних температур воздуха за осенний период;

- выбор модели прогнозирования будущих значений временного ряда на ретроспективном участке;

- оценка качества модели с помощью показателей и критериев точности.

Материалом данного исследования являются значения средних температур атмосферного воздуха за осенний период, характерных для г. Нальчика Юга России.

Исследование проводится с помощью модели ARIMA, реализованной в пакете статистических программ SPSS

Обычно для понимания изменения климата прогнозируется динамика климатических параметров. Что касается температурного режима, то это значения средних сезонных и годовых температур, а также экстремально высоких и низких температур воздуха. Материалом данного исследования являются многолетние значения температур, осредненные за три осенних месяца (сентябрь, октябрь и ноябрь). Выбор этих параметров оправдан их применением в климатологии, особенно строительной, а также в сельском хозяйстве.

Объектом данного исследования является температурный режим г. Нальчика, расположенного в предгорной зоне Юга России. Средние показатели температуры воздуха в этом городе колеблются от +25…+28 °C – в июле, до −3…−5 °С − в январе. Среднегодовая температура воздуха составляет 9,6 °С. Самая высокая температура воздуха наблюдается в конце июля, а наиболее низкая – в конце января или в начале февраля. Возможны оттепели зимой до +15 °С и выше. Характерной особенностью климата города Нальчика являются значительные суточные колебания температуры, связанные с горно-долинным ветром.

Многолетние значения средних температур воздуха за осенний период по метеостанции г. Нальчика с 1961 по 2022 гг. были предоставлены Северо-Кавказским управлением по гидрометеорологии и мониторингу окружающей среды.

В ходе исследования временной ряд температуры атмосферного воздуха разбивается на две части: 1961-2016 гг. и 2017-2022 гг. Анализ ряда проводится для первой части, а для второй прогнозируются значения средних температур воздуха и сравниваются с фактическими значениями ряда (ретропрогнозирование).

Для данного исследования применяется одна из наиболее распространенных статистических моделей, получившая название модели Бокса-Дженкинса

Согласно методологии Бокса-Дженкинса модель  состоит из трех частей

Модель  в общем случае имеет вид:

(1)

где – константа модели;

– коэффициенты авторегрессии;

– коэффициенты скользящего среднего;

– случайная ошибка или «белый шум».

Моделирование временного ряда при помощи  включает в себя следующие этапы: подготовка данных, выбор и идентификация модели (определение параметров ,  и ), оценка качества модели с помощью показателей и критериев точности и прогнозирование временного ряда на ретроспективном участке

Предварительное рассмотрение значений временного ряда показало отсутствие пропущенных значений и выбросов (данные наблюдений аномально далекие от других значений временного ряда). Далее временной ряд исследуется на стационарность. Динамика изменений средних температур воздуха (рис. 1а), свидетельствует о наличии тренда, причем имеет место его увеличение с течением времени, т.е. исходный временной ряд является нестационарным.

Рисунок 1 - Динамика изменения значений средних температур воздуха с нанесенным трендом

Примечание: а) исходный ряд; б) стационарный

DOI:10.23670/IRJ.2023.134.94.1

Процедура взятия разности первого порядка  преобразовала исследуемый ряд в стационарный  (рис. 1б), в результате появилась постоянная средняя, вокруг которой колеблются значения ряда.

Далее проводилась оценка параметров  и  модели по автокорреляционной и частной автокорреляционной функциям (рис. 2).

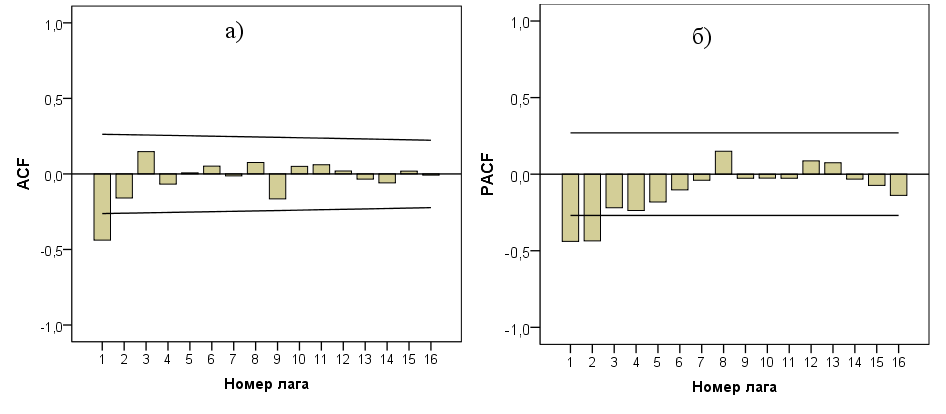
Рисунок 2 - Автокорреляционная ACF (а) и частная автокорреляционная PACF (б) функции

DOI:10.23670/IRJ.2023.134.94.2

Порядок скользящей средней  определялся как число значимых лагов автокорреляционной функции ACF (рис. 2а). Наиболее высоким оказался коэффициент автокорреляции первого порядка . Порядок модели авторегрессии выбирался по графику PACF (рис. 2б), на котором выделяется лаг 2, как последний ненулевой элемент, т.е. имеем модели  и . Выбор пал на модели-кандидаты  и  с константами и без.

Значения ACF демонстрируют медленное затухание и наличие во временном ряду средних температур воздуха периодической составляющей. Величина периода колебания равна величине лага, при котором коэффициент корреляции выделяется. В данном случае это 9 лаг, но с учетом взятия разности первого порядка мы имеем 10-летний цикл. Не подлежит сомнению, что это – результат проявления 11-летнего цикла солнечной активности

Отбор наилучшей из этих моделей проводился по:

- информационному критерию BIC;

- тесту Льюнга–Бокса на отсутствие автокорреляции в остатках;

- тесту Колмогорова-Смирнова на нормальность распределения остатков.

Нормализованный байесовский информационный критерий BIC

(2)

где  – самый низкий показатель BIC;

– показателей моделей-кандидатов.

Из двух моделей предпочтение отдается модели с меньшим значением .

Значения вероятностей для всех моделей-кандидатов, оказались равными .

Уровни значимости теста Льюинга-Бокса оказались очень высокие () для всех моделей-претендентов (табл. 1), следовательно, можно принять нулевую гипотезу об отсутствии автокорреляции в остатках по всем моделям.

Отклонение остатков от нормального распределения считается существенным, если уровень значимости теста Колмогорова-Смирнова принимает значение . В рассматриваемом случае , т.е. остатки не отклоняются от нормального распределения.

Это свидетельствует о том, что все модели-кандидаты равнозначны.

Самыми популярными критериями выбора модели являются средняя абсолютная ошибка MAPE, характеризующая точность прогноза и коэффициент детерминации , показывающий доля дисперсии объясняемую моделью.

Анализ значений MAPE и  отменил модели  с константой и без (табл. 1).

Таким образом, на этапе идентификации остались две модели-кандидаты  с константой и без константы.

Дальнейший выбор адекватной модели основывался на прогнозировании значений временного ряда на ретроспективном участке с 2017 по 2022 гг. (рис. 3). На рисунке 3 приведены фактические значения средних осенних температур воздуха и их прогнозные значения.

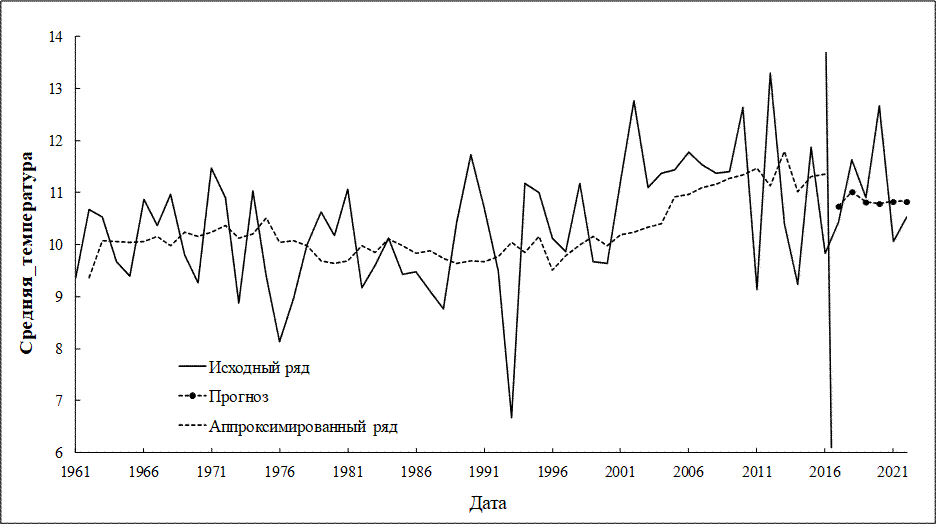
Рисунок 3 - Динамика значений средних осенних температур воздуха

Примечание: исходный ряд (сплошная кривая), аппроксимированный ряд (штриховая кривая) и прогнозные значения с 2017 по 2022 гг. (штрихпунктирная)

DOI:10.23670/IRJ.2023.134.94.4

Были рассчитаны абсолютные ошибки модели прогноза на ретроспективном участке – MAPE (табл. 2) по фактическим и прогностическим значениям исследуемого ряда.

Модель  без константы оказалась наилучшей, так как средняя абсолютная ошибка прогноза по этой модели оказалась минимальной и равной 5,70; сама процедура взятия первой разности временного ряда также отменяет константу модели.

Из литературы известно, что значение MAPE<10% свидетельствует о высокой точности моделей прогнозов.

Анализ динамики временного ряда значений средних температур воздуха за осенний период показал наличие периодичности, вызванной 11-летним периодом солнечной активности.

Средняя относительная ошибка прогноза на ретроспективном ряде, равная ≈6%, свидетельствует о высокой точности предлагаемой модели .

Анализ эффективности выбранной модели показал, что критерии качества прогнозирования значений средних осенних температур атмосферного воздуха по предлагаемой модели  удовлетворяет всем критериям и требованиям качества и адекватности, предъявляемым к моделям прогнозирования.

Это свидетельствует о том, что такой сложный по своей природе временной ряд, характеризующий температурный режим атмосферного воздуха может прогнозировать по модели Бокса-Дженкинса.