ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ВАКУУМНОЙ ПАНЕЛИ ЯЧЕИСТОЙ СТРУКТУРЫ

ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ВАКУУМНОЙ ПАНЕЛИ ЯЧЕИСТОЙ СТРУКТУРЫ

Научная статья

Балалаев А.Н.^1, *, Тимкин Д.М.²

¹ ORCID: 0000-0003-0839-6858;

² ORCID: 0000-0002-6627-2151;

^{1, 2} Самарский университет путей сообщения, Самара, Россия

* Корреспондирующий автор (wagon.samgaps[at]mail.ru)

Аннотация

Предложена методика экспериментального определения удельного теплового сопротивления вакуумной теплоизоляции, найдены значения теплового сопротивления вакуумной панели ячеистой структуры при различной величине остаточного давления внутри панели. Составлена 3-D модель стенда для экспериментального определения удельного теплового сопротивления вакуумной теплоизоляции, выполнены тепловые исследования модели стенда в SolidWorks Simulation. С помощью метода конечных элементов определены значения теплового сопротивления модели вакуумной панели с учетом передачи тепла теплопроводностью и конвекцией. Расхождения в результатах теоретического и экспериментального определения теплового сопротивления вакуумной панели составили 7,9%.

Ключевые слова: вакуумная теплоизоляция, ячеистая структура, удельное тепловое сопротивление, экспериментальные исследования, теоретические исследования.

THEORETICAL AND EXPERIMENTAL STUDIES OF A VACUUM PANEL WITH A CELLULAR STRUCTURE

Research article

Balalaev A.N.^1, *, Timkin D.M.²

¹ ORCID: 0000-0003-0839-6858;

² ORCID: 0000-0002-6627-2151;

^{1, 2} Samara State Transport University, Samara, Russia

* Corresponding author (wagon.samgaps[at]mail.ru)

Abstract

The current study proposes a method of experimental determination of the specific thermal resistance of vacuum thermal insulation, finds the values of the thermal resistance of a vacuum panel with a cellular structure at different values of the residual pressure inside the panel. The authors present a 3-D model of the stand for the experimental determination of the specific thermal resistance of vacuum thermal insulation and perform thermal studies of the stand model via SolidWorks Simulation. The values of the thermal resistance of the vacuum panel model are also determined using the finite element method, taking into account the heat transfer by thermal conductivity and convection. The differences in the results of the theoretical and experimental determination of the thermal resistance of the vacuum panel amount to 7.9%.

Keywords: vacuum thermal insulation, cellular structure, specific thermal resistance, experimental studies, theoretical studies.

Введение

Вакуумная теплоизоляция используется в криогенной и космической технике, однако, с появлением полимерных материалов повышенной прочности и технологий 3-D печати появилась возможность использования вакуумных панелей ячеистой структуры в самых разных отраслях техники.

В [1, С. 50] предложено использовать вакуумные панели сотового сечения в качестве несущих стен кузовов пассажирских и рефрижераторных железнодорожных вагонов, исследовались их прочностные, массовые и теплоизоляционные характеристики. В [2, С. 13] предложено разделить функции несущей конструкции и теплоизоляции у кузовов пассажирских вагонов, в которых вакуумные панели ячеистой структуры выполняли роль только теплоизоляции. Исследования теплоизоляционных свойств таких панелей в [2, С. 14, 15] выполнялось в SolidWorks Simulation с помощью метода конечных элементов с учетом передачи тепла за счет теплопроводности.

Исследования теплоизоляционных свойств экструдированных алюминиевых панелей с ребрами жесткости из полиамида проводилось в [3, С. 58-60] аналитическими методами с учетом передачи тепла теплопроводностью, радиацией и конвекцией. Внутреннюю полость таких панелей в [3, С. 58] было предложено вакуумировать до остаточного давления 1…3 кПа.

Экспериментальные исследования вакуумных панелей ячеистой структуры затруднены тем, что из-за большой величины удельного теплового сопротивления вакуумной теплоизоляции для использования стационарного теплового режима требуется длительное время выхода на режим, в течение которого необходимо поддерживать неизменные условия теплового режима. Этого недостатка лишен способ измерения удельного теплового сопротивления вакуумной теплоизоляции [4], основанный на использовании регулярного теплового режима.

Целью данной работы является экспериментальные исследования опытного образца вакуумной теплоизоляции по методу [4] и теоретические исследования 3-D модель стенда для экспериментального определения удельного теплового сопротивления вакуумной теплоизоляции в SolidWorks Simulation с помощью метода конечных элементов.

Методы и принципы исследования

Согласно способу измерения удельного теплового сопротивления вакуумной теплоизоляции [4], необходимо сформировать тепловой поток через два одинаковых эталонных объекта с малой величиной удельного теплового сопротивления, например, через две квадратные медные пластины – см. рисунок 1. Это необходимо для равномерного распределения температуры в этих эталонных объектах и деления теплового потока на примерно равные части. С первым эталонным объектом совмещен равный по высоте и ширине исследуемый объект – опытный образец вакуумной пластины сотового сечения. Со вторым эталонным объектом совмещен равный по высоте и ширине третий эталонный объект с большой величиной удельного теплового сопротивления, например, пенополистирол с теплопроводностью λ_et = 0,037 Вт/(м К). Толщины третьего эталонного объекта и исследуемого объекта подбираются равными. Нагрев первого 2 и второго 5 эталонных объектов от нагревателя 1 (см. схему стенда на рисунке 1) осуществляется с помощью электрической спирали за счет радиационного теплообмена, поэтому потоки тепла через объекты 1 и 5 примерно равны. Однако, темпы повышения температуры эталонных объектов 1 и 5 может быть разной в зависимости от соотношений величин удельного теплового сопротивления третьего эталонного объекта 9 и исследуемого объекта 8. Если удельное тепловое сопротивление третьего эталонного объекта 9 больше, чем у исследуемого объекта 8, то темп нагрева второго эталонного объекта 5 должен быть выше, чем у первого эталонного объекта 2. Сущность способа [4] заключается в том, что сначала для экспериментального стенда строится тарированная зависимость разности интервалов времени, в течение которых температура первого 2 и второго 5 эталонных объектов повышается на заданную величину, от отношения величин удельного теплового сопротивления третьего эталонного объекта 9 и вариантов четвертого эталонного объекта, который замещает исследуемый объект 8.

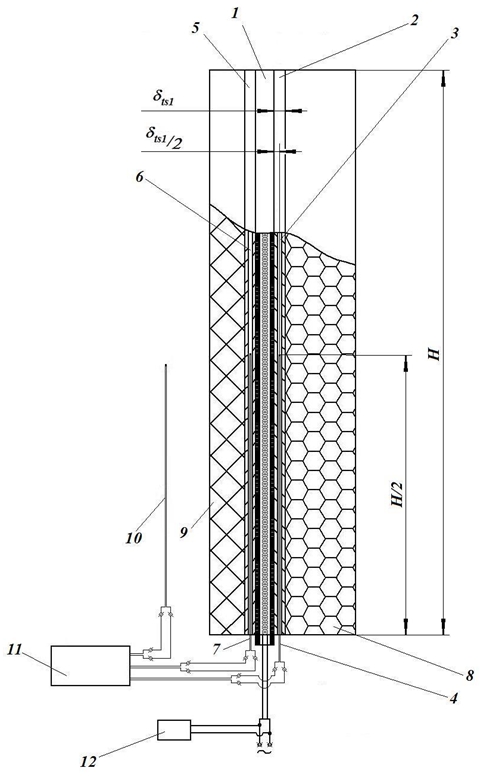
Рис. 1 – Схема стенда для измерения удельного теплового сопротивления вакуумной теплоизоляции:

1 – источник тепловой энергии; 2 – первый эталонный объект; 3 – паз в первом эталонном объекте; 4 – первый измеритель температуры; 5 – второй эталонный объект; 6 – паз во втором эталонном объекте; 7 – второй измеритель температуры; 8 – исследуемый объект; 9 – третий эталонный объект; 10 – третий измеритель температуры; 11 – электронный блок обработки измерения температуры; 12 – прибор измерения электрической мощности

 

Варианты четвертого эталонного объекта подбираются с такой же толщиной, что и толщины третьего эталонного объекта 9 и исследуемого объекта 8, но с различными значениями коэффициента теплопроводности λ_et4. В этом случае отношение величин удельного теплового сопротивления третьего эталонного объекта 9 и вариантов четвертого эталонного объекта равно отношению λ_et4/ λ_et, так как для однородных сплошных твердых тел удельное тепловое сопротивление R равно отношению толщины тела δ к коэффициенту теплопроводности λ.

Для измерения температур первого 2 и второго 5 эталонных объектов в них предусмотрены внутренние пазы 3 и 6, в которых размещены измерители температуры 4 и 7 (термопары).

После получения тарированной зависимости стенда вместо четвертого эталонного объекта устанавливается исследуемый объект 8, определяется разность интервалов времени повышения температуры первого 2 и второго 5 эталонных объектов на заданную величину, по этой разности из тарированной зависимости находится отношение удельного теплового сопротивления третьего эталонного объекта 9 к удельному тепловому сопротивлению исследуемого объекта 8 – R_et/R_x.

В ходе всех экспериментов необходимо поддерживать одинаковую температуру окружающей среды, контролируемую третьим измерителем температуры 10, и одинаковую электрическую мощность, подаваемую на электрическую спираль источника тепловой энергии 1, и контролируемую прибором измерения электрической мощности 12.

При построении тарированной зависимости стенда для четвертого эталонного объекта использовались материалы: бальза (λ_et4 = 0,05 Вт/(м К)), резина (λ_et4 = 0,14 Вт/(м К)), стекло (λ_et4 = 0,75 Вт/(м К)), пластик ABS (λ_et4 = 0,2256 Вт/(м К), у которых удельное тепловое сопротивление меньше, чем у третьего эталонного объекта – пенополистирола, то есть она справедлива только для области R_et/R_x > 1. Поэтому использование тарированной зависимости стенда в области R_et/R_x < 1 может привести к значительным погрешностям.

Для обоснования возможности использования тарированной зависимости стенда в области R_et/R_x < 1 была построена его 3-D модель, которая исследовалась с помощью метода конечных элементов в SolidWorks Simulation. Методика тепловых исследований вакуумной панели сотового сечения описана в [5, С. 50, 51, 120-122], однако, для моделирования работы экспериментального стенда потребовались некоторые изменения.

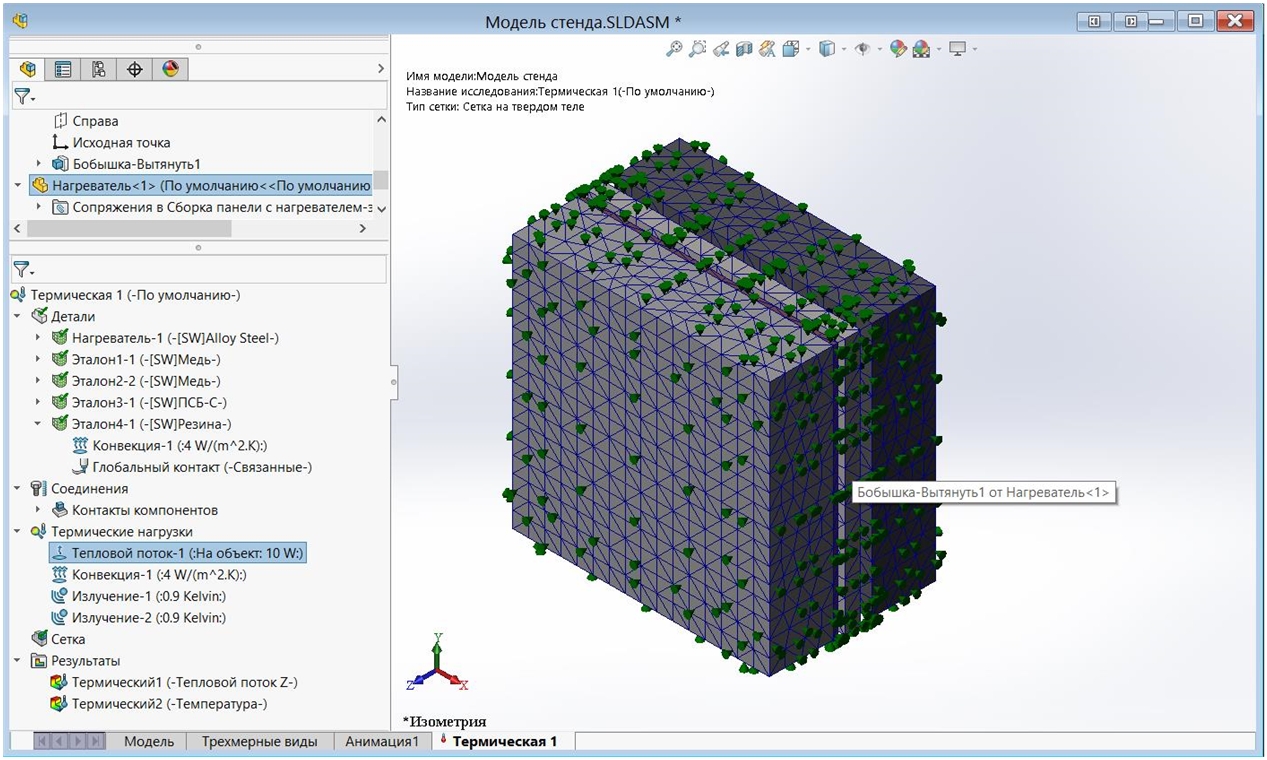
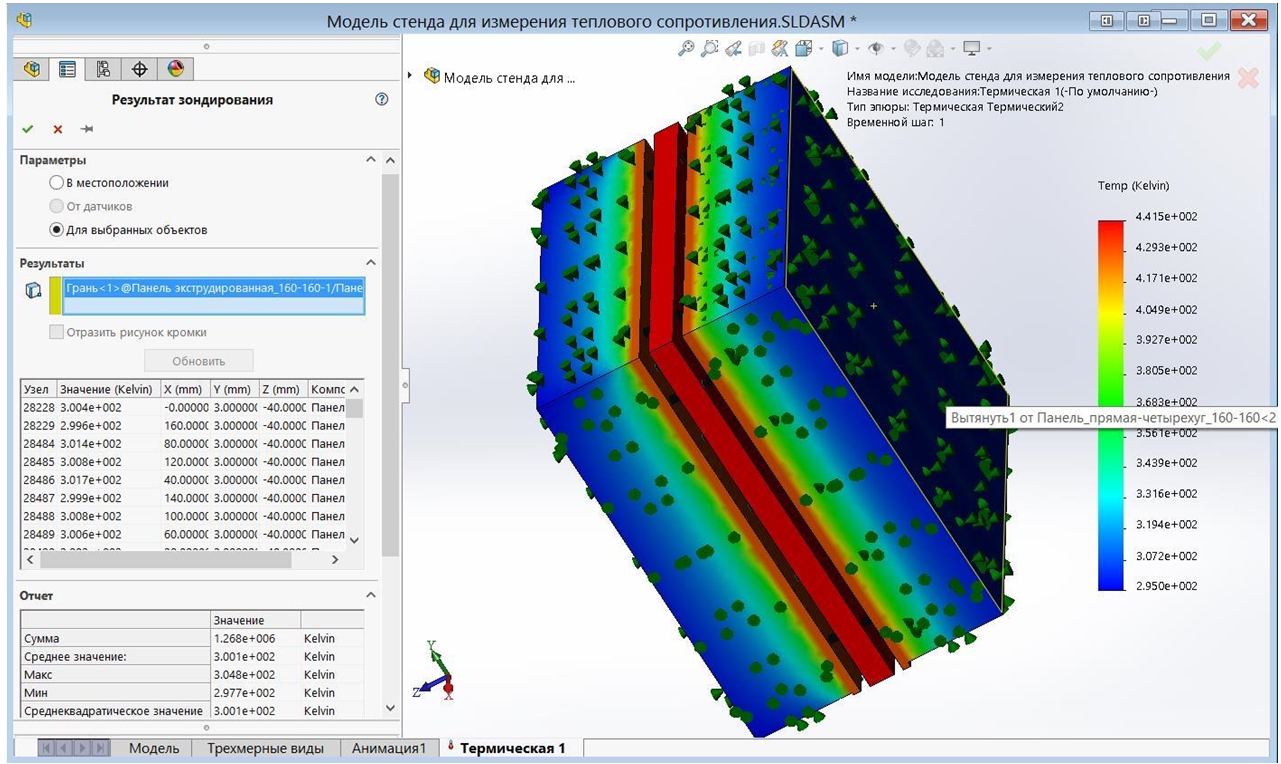
На рисунке 2 представлена модель стенда для измерения удельного теплового сопротивления объектов, где в качестве исследуемого объекта установлен четвертый эталон («Эталон 4») из материала «резина».

Рис. 2 – Модель стенда для измерения удельного теплового сопротивления объектов в тепловом исследовании SolidWorks Simulation

 

Как видно на рисунке 2, к модели нагревателя приложена нагрузка в виде тепловой мощности 10 Вт. Эта мощность тепловыделения расходуется на радиационное излучение в виде двух нагрузок: «Излучение 1» и «Излучение 2», для которых указаны грани нагревателя, первого эталона («Эталон 1») и второго эталона («Эталон 2»). Ко всем внешним граням приложена тепловая нагрузка типа «Конвекция», в которой заданы температура окружающей среды T_н = 293 К и коэффициент теплоотдачи α_н = 4 Вт/(м² К).

На модели стенда (рисунок 1) построена сетка конечных элементов с максимальным размером ∆_max = 10 мм, минимальным размером ∆_min = 3 мм и числом конечных элементов 21473. Решающая программа Direct Sparse выполняет решение за 56 сек.

После получения результатов в виде эпюры удельного теплового потока в направлении оси Z и эпюры распределения температуры производится зондирование по всему «Эталону 4» для получения среднего значения удельного теплового потока W_Z и по двум граням «Эталона 4» для получения средних величин температуры на входе теплового потока T_max и на выходе теплового потока по оси Z – T _min. Если разделить разность температур (T_max - T _min) на величину W_Z, то получается значение удельного теплового сопротивления «Эталона 4».

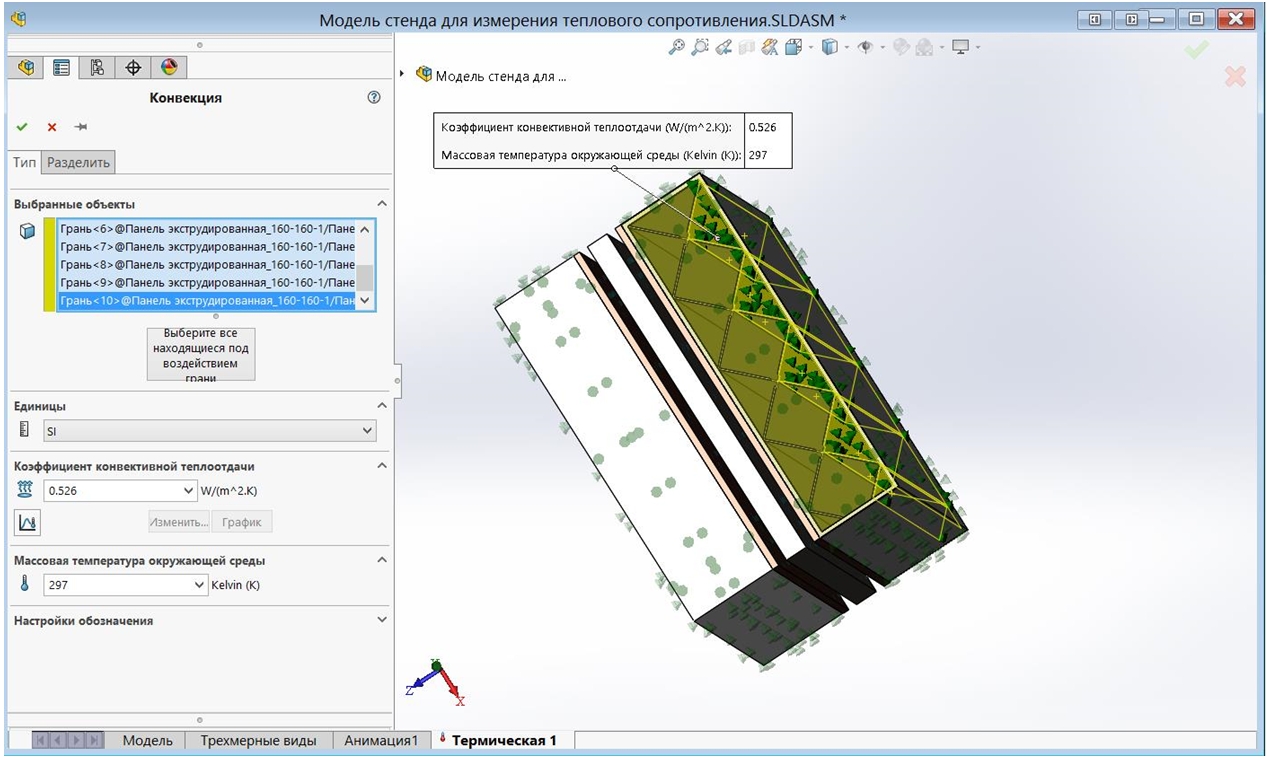
Для модели стенда измерения удельного теплового сопротивления вакуумной панели методика теплового исследования в SolidWorks Simulation отличается добавлением тепловых нагрузок типа «Конвекция» для трех внутренних полостей вакуумной панели, как показано на рисунке 3. Чтобы задать эти нагрузки одна из стенок модели вакуумной панели переведена в режим «Прозрачный». При задании этих нагрузок для каждой внутренней полости задавались коэффициент теплоотдачи и температура воздуха. Приближенно, температуры воздуха в полостях рассчитывались последовательными приближениями в допущении линейного распределения температуры по толщине вакуумной панели.

Рис. 3 – Нагрузка типа «Конвекция» для внутренних полостей вакуумной панели

  Коэффициент теплоотдачи в полостях вакуумной панели находится для свободной конвекции согласно [6, С. 185] из уравнения подобия     (1)

где Nu_a, Gr_a Pr_a – критерии подобия Нуссельта, Грасгофа и Прандтля находятся по плотности и теплотехническим параметрам при температуре воздуха – см. [6, С. 182, 183]. После подстановки в формулу (1) выражений для критериев подобия (см. [6, С. 164]) получается выражение для коэффициента теплоотдачи в полостях вакуумной панели

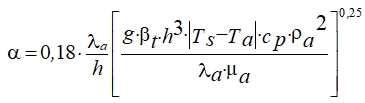   (2)

где λ_a = 0,0232 Вт/(м К) – коэффициент теплопроводности воздуха; h = 0,025 м – высота ячейки сот вакуумной панели; g = 9,8 м/с² – ускорение свободного падения, β_t = 0,0034 – коэффициент объемного расширения воздуха; T_s, T_a – температура стенки и воздуха; a_a, ν_a – коэффициенты температуропроводности и кинематической вязкости воздуха. С учетом того, что коэффициент температуропроводности равен отношению коэффициента теплопроводности к произведению удельной теплоемкости при постоянном давлении и плотности, а коэффициент кинематической вязкости равен отношению коэффициента динамической вязкости к плотности формула (2) переписывается следующим образом

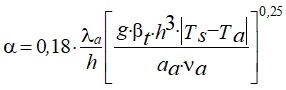    (3)

где c_p = 1005 Дж/(кг К) – удельная теплоемкость воздуха при постоянном давлении; ρ_a = P_a/(R T_a) – плотность воздуха, P_a – давление воздуха в полостях вакуумной панели; R = 287 Дж/(кг К) – индивидуальная газовая постоянная для воздуха; μ_a – коэффициент динамической вязкости воздуха.

Коэффициент динамической вязкости воздуха находится по формуле Сазерленда в зависимости от температуры [7, Прил. 5]

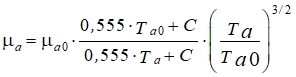   (4)

где μ_a = 18,27×10^-6 Па сек; T_a0 = 291,15 К; С = 120 – константа Сазерленда [8, С. 42-44].

В ходе теплового исследования коэффициент теплоотдачи a воздуха внутри полостей вакуумной панели рассчитывался при различных значениях давления внутри панели.

Основные результаты

Для проведения эксперимента был спроектирован и изготовлен методом 3-D печати опытный образец вакуумной панели сотового сечения в соответствии с [9], [10] из полиамида марки Ultran 630. Модель опытного образца с габаритными размерами 160×160×40 мм показана на рисунке 10.

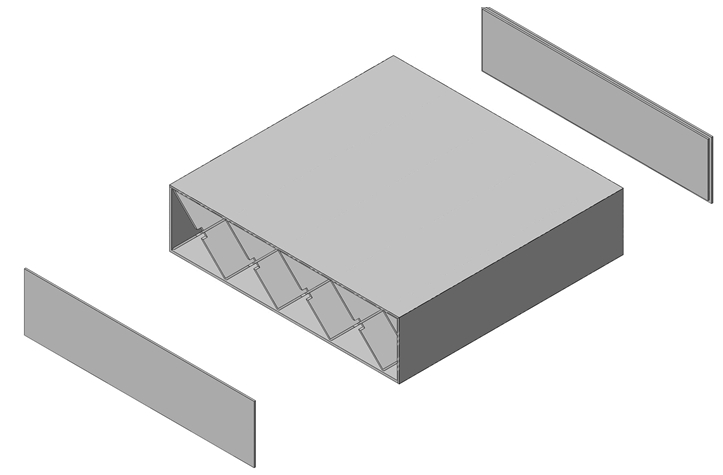
Рис. 4 – Модель опытного образца вакуумной панели

 

Как видно на рисунке 4, в конструкции опытного образца были предусмотрены две заглушки, которые закрывали открытые торца панели. После герметизации торцов через штуцер в одной из заглушек при помощи вакуум-насоса создавалось пониженное давление внутри панели.

На рисунке 5 показан стенд для измерения удельного теплового сопротивления вакуумной панели при различной величине остаточного давления в ее внутренней полости.

Рис. 5 – Стенд для измерения удельного теплового сопротивления вакуумной панели

Как показано на рисунке 5, остаточное давление внутри вакуумной панели измеряется с помощью вакуумметра модели ВПЗ-УФ класса точности 1,5 (производитель АО «ПО Физтех»), температура в медных пластинах («Эталон 1» и «Эталон 2») измерялась термопарами К-типа, регистрировалась двумя приборами CENTER-314 (погрешность 0,2%), которые также регистрировали температуру и относительную влажность окружающей среды.

В качестве «Эталона-3» использовался пенополистирол экструдированный с габаритными размерами 160´160´40 мм. На первом этапе экспериментов для построения тарированной зависимости стенда в качестве «Эталона-4» использовались пластины с габаритными размерами 160´160´40 мм из материалов: бальза, резина, стекло и пластик ABS. Результаты этих испытаний в виде тарированной зависимости представлены на рисунке 6.

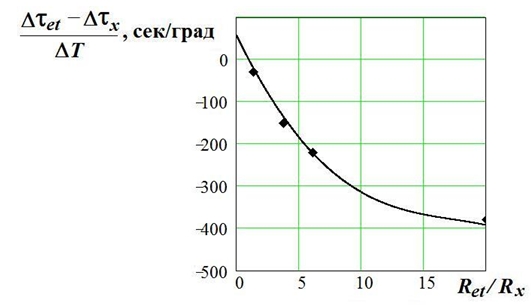
Рис. 6 – Тарированная зависимость стенда для измерений удельного теплового сопротивления вакуумной панели

  Как видно на рисунке 6, через экспериментальные точки проходит кривая линия, аппроксимируемая зависимостью     (5)

здесь Y(Z) представляет собой ординату, а Z – абсциссу.

При замене «Эталона 4» на вакуумную панель для обработки эксперимента удобнее использовать тарированную зависимость в виде полинома (4), где Y(Z) представляет собой абсциссу, а Z – ординату. На рисунке 7 представлены результаты испытаний вакуумной панели при значениях остаточного давления во внутренней полости вакуумной панели Р_ост = 100 кПа; 50 кПа; 25 кПа; 1 кПа.

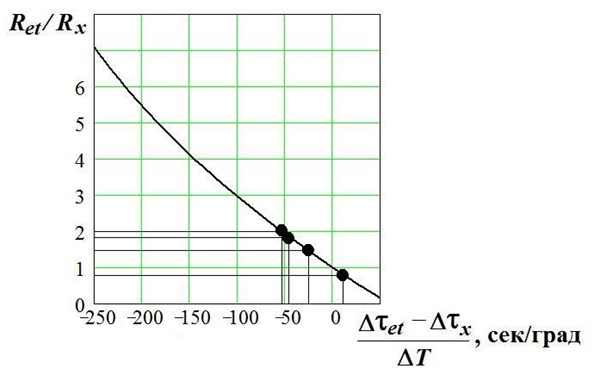
Рис. 7 – Результаты экспериментов над вакуумной панелью

 

Как видно из графика рисунка 7, минимальное значение отношения R_et/R_x составило 0,8. Так как удельное тепловое сопротивление «Эталона-3» известно (R_et = δ/l_et = 0,04/0,037 = 1,081 (м² К)/Вт), то R_{x min} = 1,35 (м² К)/Вт. Это значение получено в эксперименте, когда остаточное давление в полости вакуумной панели составляло 1 кПа.

Для верификации проведенных экспериментов в области тарированной кривой R_et/R_x < 1 была исследована 3-D модель стенда для измерения удельного теплового сопротивления вакуумной панели в программе SolidWorks Simulation с параметрами нагрузки типа «Конвекция» для внутренних полостей вакуумной панели: в первой полости (как показано на рисунке 3) – a = 0,289 Вт/(м² К), Т_а = 330 К; во второй полости – a = 0,241 Вт/(м² К), Т_а = 361 К; в третьей полости – a = 0,185 Вт/(м² К), Т_а = 392 К. Эти значения соответствуют величине остаточного давления 1 кПа.

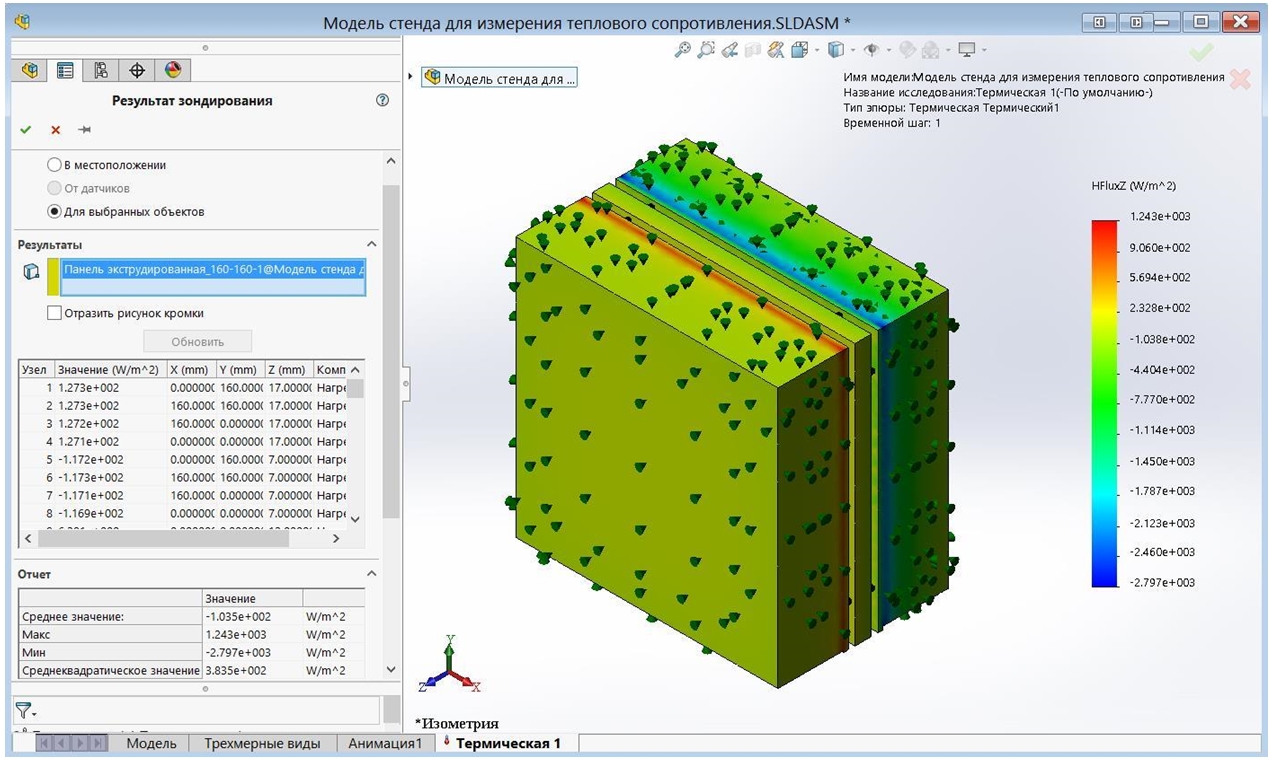
На рисунке 8 представлены результаты зондирования модели вакуумной панели по удельному тепловому потоку вдоль оси Z.

Рис. 8 – Результаты расчета удельного теплового потока через вакуумную панель

 

Как видно на рисунке 8, среднее значение удельного теплового потока через вакуумную панель составило – W_Z = 103,5 Вт/м².

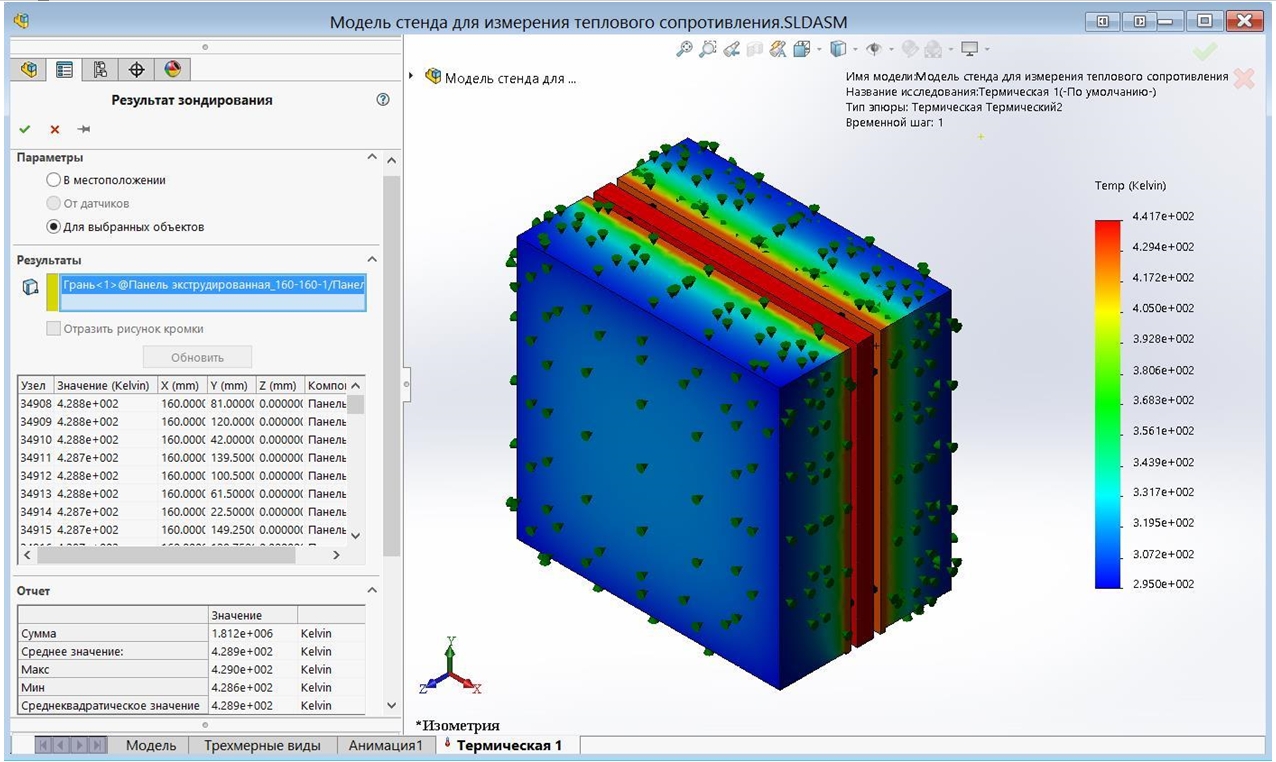
На рисунках 9 и 10 представлены результаты зондирования двух граней вакуумной панели с размерами 160´160 мм по температуре.

Рис. 9 – Результаты расчета температуры нагреваемой грани вакуумной панели

Рис. 10 – Результаты расчета температуры охлаждаемой грани вакуумной панели

 

Как видно на рисунках 9 и 10, разность температур нагреваемой и охлаждаемой граней вакуумной панели составляет (T_max - T _min) = 428,9 – 300,1 = 128,8 К. При делении этой разности на величину W_Z получается расчетное значение удельного теплового сопротивления вакуумной панели вдоль оси Z: R_x=128,8/103,5=1,244 (м² К)/Вт. В данных исследованиях использовалась сетка конечных элементов с максимальным размером ∆_max = 5 мм, минимальным размером ∆_min = 0,7 мм и числом конечных элементов 124744. Решающая программа Direct Sparse выполнила решение за 42 мин. 31 сек. Дальнейшее уменьшение ∆_max и ∆_min приводило к исчерпанию оперативной памяти компьютера.

Такие же расчеты проводились для пенополистирола («Эталон 3»). Результаты составили: разность температур нагреваемой и охлаждаемой граней «Эталона-3» составляет (T_max - T _min) = 427,7 – 310 = 117,7 К, величина удельного теплового потока вдоль оси Z – W_Z = 112,4 Вт/м². Значение удельного теплового сопротивления «Эталона 3» вдоль оси Z: R_x=117,7/112,4=1,047 (м² К)/Вт.

Обсуждение

Верификация конечно-элементной модели стенда для измерения удельного теплового сопротивления вакуумной панели заключается в сравнении известных значений удельного теплового сопротивления пенополистирола («Эталон 3») с аналогичными параметрами, рассчитанными в тепловых исследованиях SolidWorks Simulation. Сравнение показало, что расхождение рассчитанных и известных значений составило 3,1%.

Для верификации экспериментов над опытным образцом вакуумной панели в области тарированной кривой R_et/R_x < 1 проведено сравнение значений удельного теплового сопротивления вакуумной панели, полученных экспериментально и рассчитанных в тепловых исследованиях SolidWorks Simulation. Расхождение составило 7,9%. Было отмечено, что уменьшение максимального размера сетки конечных элементов с ∆_max = 10 мм до ∆_max = 5 мм снижает расхождение расчетных и экспериментальных значений с 28,9% до 7,9%. Дальнейшее снижение максимального размера сетки было ограничено располагаемой оперативной памятью компьютера (16 Гб).

Таким образом, среднеквадратичное отклонение всех сравниваемых параметров в экспериментальных и теоретических исследованиях вакуумной панели составило 8,5%.

Заключение

Предложена методика экспериментального определения удельного теплового сопротивления вакуумной теплоизоляции, создан стенд для измерения удельного теплового сопротивления вакуумной панели ячеистой структуры, экспериментально найдены значения теплового сопротивления вакуумной панели при различной величине остаточного давления внутри панели. При остаточном давлении 1 кПа величина удельного теплового сопротивления опытного образца вакуумной панели составила 1,35 (м² К)/Вт, что на 25% больше удельного теплового сопротивления пенополистирола таких же габаритных размеров.

Разработана 3-D модель стенда для определения удельного теплового сопротивления вакуумной теплоизоляции, выполнены тепловые исследования модели стенда в SolidWorks Simulation. В тепловых исследованиях модели вакуумной панели ячеистой структуры учитывалась передача тепла теплопроводностью и конвекцией, коэффициент теплоотдачи рассчитывался из уравнения подобия для свободной конвекции в ограниченном пространстве с учетом низкого давления во внутренней полости вакуумной панели. Расхождения значений удельного теплового сопротивления вакуумной панели, полученных экспериментально и рассчитанных в тепловых исследованиях SolidWorks Simulation, составили 7,9%. Расхождение рассчитанных и известных значений удельного теплового сопротивления пенополистирола составило 3,1%. Среднеквадратичное отклонение всех сравниваемых параметров в экспериментальных и теоретических исследованиях вакуумной панели составило 8,5%.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References*

1. Balalaev A. Mass and heat-insulation properties of the bodies of passenger and insulated railway cars made of vacuum honeycomb panels / A. N. Balalaev, M, Parenyuk, I. Arslanov et al. // Journal of Applied Engineering Science, 2018, V. 16, br. 1, P. 50-59.
2. Балалаев А. Н. Исследование модели вакуумной теплоизоляции пассажирского вагона / А. Н. Балалаев, М. А. Паренюк, Г. М. Сергеев и др. // Вестник транспорта Поволжья. 2018. № 2. С. 13-20.
3. Балалаев А. Н. Теплотехнические свойства вагонов и контейнеров из экструдированных алюминиевых панелей / А. Н. Балалаев, А. С. Мокшанов, М. А. Паренюк // Транспорт Российской Федерации, 2014. - №1. - С. 58-60.
4. Пат. 2736322 Российская Федерация, МПК7 G01N 25/18. Способ измерения удельного теплового сопротивления и устройство для его осуществления / Балалаев А. Н., Паренюк М. А., Тимкин Д. М.; заявитель и патентообладатель Самарский государственный университет путей сообщения. – № 2018146922; заявл. 26.12.2018; опубл. 13.11.20; Бюл. №32. – 16 с.
5. Балалаев А. Н. Проектирование наземных транспортных средств с использованием сотовых конструкций: монография / А. Н. Балалаев, А. М. Зиятдинов, М. А. Паренюк и др. – Самара: СамГУПС, 2019. – 196 с.
6. Карминский В. Д. Техническая термодинамика и теплопередача: Курс лекций / В. Д. Карминский. – М.: Маршрут, 2005. – 224 с.
7. Flow of Fluids Through Valves, Fittings & Pipe. Technical Paper No. 410, Crane Co. – London : Vervante, 1999. – 114 p.
8. Handbook of Chemistry and Physics. 65th edition / editor R. C. Weast. Florida : CRC Press, Inc. Boca Raton, 1984. – 1254 p.
9. Патент на полезную модель РФ № 182546, МПК E04B 2/02, E04B 1/80, E04C 1/40. Теплоизолирующая стенка / А.Н. Балалаев, М.А. Паренюк, Г.М. Сергееев, Д.М. Тимкин. Заявка № 2018104342 от 05.02.2018. Опубл. 22.08.2018. Бюл. № 24. – 8 с.
10. Патент РФ на изобретение №2553629, F16L59/065. Способ изготовления вакуумного теплоизоляционного изделия / А.Н. Балалаев, А.С. Мокшанов, Д.А. Попов. - Заявка № 2013153611/06; Заявлено 03.12.2013; Опубл. 20.06.15; Приоритет 03.12.2013 // Изобретения. Полезные модели. - 2015. - №17. – 8 с.

Список литературы на английском языке / References in English

1. Balalaev A. Mass and heat-insulation properties of the bodies of passenger and insulated railway cars made of vacuum honeycomb panels / A. N. Balalaev, M, Parenyuk, I. Arslanov et al. // Journal of Applied Engineering Science, 2018, vol. 16, br. 1, p. 50-59.
2. Balalaev A. N. Issledovaniye modeli vakuumnoy teploizolyatsii passazhirskogo vagona [Study of vacuum heat-insulation of the passenger car] / A. N. Balalaev, M. A. Parenyuk, G. M. Sergeev et al. // Vestnik transporta Povolzhya [Bulletin of transport of the Volga region]. – 2018. – № 2. – P. 13–20. [in Russian]
3. Balalaev A. N. Teplotekhnicheskiye svoystva vagonov i konteynerov iz ekstrudirovannykh alyuminiyevykh paneley [Thermal properties of wagons and containers made of extruded aluminum panels] / A. N. Balalaev, A. S. Mokshanov, M. A. Parenyuk // Transport Rossiyskoy Federatsii [Transport of the Russian Federation]. – 2014. – № 1. – P. 58–60. [in Russian]
4. Pat. 2736322 Russian Federation, MPK7 G01N 25/18. Sposob izmereniya udelnogo teplovogo soprotivleniya i ustroystvo dlya ego osushchestvleniya [Method of measuring the specific thermal resistance and the device for its implementation] / Balalaev A. N., Parenyuk M. A., Timkin D. M.; the applicant and the patentee Samara State Transport University. – № 2018146922; appl. 12/26/18; publ. 11/13/20, Bul. Number 32. – 16 p. [in Russian]
5. Balalaev A. N. Proyektirovaniye nazemnykh transportnykh sredstv s ispolzovaniyem sotovykh konstruktsiy: monografiya [Designing ground vehicles using cellular structures: monograph] / A. N. Balalaev, A. M. Ziyatdinov, M. A. Parenyuk et al. – Samara : SSTU, 2019. – 196 p. [in Russian]
6. Karminskiy V. D. Tekhnicheskaya termodinamika i teploperedacha: Kurs lektsiy [Technical thermodynamics and heat transfer: A course of lectures] / V. D. Karminsky. – M. : Marshrut, 2005. – 224 p. [in Russian]
7. Flow of Fluids Through Valves, Fittings & Pipe. Technical Paper No. 410, Crane Co. – London : Vervante, 1999. – 114 p.
8. Handbook of Chemistry and Physics. 65th edition / editor R. C. Weast. – Florida : CRC Press, Inc. Boca Raton, 1984. – 1254 p.
9. Pat. 182546 Russian Federation, MPK7 E04B 2/02, E04B 1/80, E04C 1/40. Teploizoliruyushchaya stenka [Heat-insulating wall] / Balalaev A. N., Parenyuk M. A., Sergeev G. M., Timkin D. M.; the applicant and the patentee Samara State Transport University. – № 2018104342; appl. 02/05/18; publ. 08/22/18, Bul. Number 24. – 8 p. [in Russian]
10. Pat. 2553629 Russian Federation, MPK7 F16L59/065. Sposob izgotovleniya vakuumnogo teploizolyatsionnogo izdeliya [Method of manufacturing a vacuum thermal insulation product] / Balalaev A. N., Parenyuk M. A., Timkin D. M.; the applicant and the patentee Samara State Transport University. – № 2013153611/06; appl. 12/03/13; publ. 06/20/15, Bul. Number 17. – 8 p. [in Russian]