ПРОЦЕДУРА ВЫЧИСЛЕНИЯ СКОРОСТИ ВЕТРА В СОВМЕСТНОЙ ГЛОБАЛЬНОЙ МОДЕЛИ КЛИМАТА

ПРОЦЕДУРА ВЫЧИСЛЕНИЯ СКОРОСТИ ВЕТРА В СОВМЕСТНОЙ ГЛОБАЛЬНОЙ МОДЕЛИ КЛИМАТА

Научная статья

Пархоменко В.П.*

ORCID: 0000-0002-9963-0496,

Вычислительный центр им. А.А. Дородницына ФИЦ ИУ РАН, Москва, Россия

* Корреспондирующий автор (vparhom[at]yandex.ru)

Аннотация

В работе рассматривается прогностическая модель глобального климата промежуточной сложности, состоящая из трехмерной гидродинамической модели мирового океана с реальной конфигурацией глубин и континентов, модели эволюции морского льда и двумерной модели атмосферы баланса и переноса влаги и тепла. Предложена процедура определения поля скоростей ветра по распределению приземной температуры атмосферы на основе геострофического подхода, учета термальной составляющей ветра и введения механизма трения о подстилающую поверхность. Это позволяет качественно верно описывать поле скоростей ветра в зависимости от характеристик климатической системы. Приведены результаты численных экспериментов с применением этой процедуры по моделированию климатических изменений при увеличении концентрации СО₂ в 21 веке.

Ключевые слова: глобальная климатическая модель, численные эксперименты.

A PROCEDURE FOR CALCULATING WIND SPEED IN A JOINT GLOBAL CLIMATE MODEL

Research article

Parkhomenko V.P.*

ORCID: 0000-0002-9963-0496,

Dorodnitsyn Computing Centre, Federal Research Center "Informatics and Management" of the Russian Academy of Sciences (FITz IU RAN), Moscow, Russia

* Corresponding author (vparhom[at]yandex.ru)

Abstract

The article examines a predictive model of the global climate of intermediate complexity, consisting of a three-dimensional hydrodynamic model of the world ocean with a real configuration of depths and continents, a model of the evolution of sea ice and a two-dimensional model of the atmosphere of balance and transfer of moisture and heat. The study proposes a procedure for determining the wind velocity field from the distribution of the surface temperature of the atmosphere based on the geostrophic approach, taking into account the thermal component of the wind and introducing a friction mechanism on the underlying surface. This allows for accurately describing the field of wind speeds depending on the characteristics of the climate system. The authors of the article present the results of numerical experiments using this procedure for modeling climate changes with an increase in the concentration of CO₂ in the 21st century.

Keywords: global climate model, numerical experiments.

Введение

Рассматривается прогностическая модель глобального климата промежуточной сложности, состоящая из пространственной гидродинамической модели океана с реальным распределением глубин и континентов, модели процессов изменения морского льда и двумерной модели атмосферы транспорта водяного пара и тепла. Подробное описание содержится в [1], [2].

Модель океана формулируется в геострофическом подходе с членом, описывающем внутреннее трение в уравнениях движения по горизонтали. Условие нулевого нормального потока задается на всех границах. Течения в верхнем слое формируются под влиянием напряжения трения ветра в нижнем слое атмосферы. Значения потоков тепла и влаги у дна принимаются равными нулю, а на поверхности связаны с процессами в атмосфере.

В прогностической модели морского льда основные уравнения определяют долю льда в ячейке и осредненную толщину льда. Изменение количества льда в модели определяется всегда соотношением потоков атмосферного тепла в океанский лед и изо льда в океан. Значение температуры верхнего слоя льда определяется диагностическим уравнением.

Характеристики атмосферы (температура, влажность, осадки) вычисляются в модели баланса влаги и тепловой энергии. В модели формулируется осредненное по высоте уравнение для температуры воздуха, соответствующее балансу падающего и излученного радиационных потоков, явных (вихревых) обменов потоками тепла с поверхностью суши или океана, выделения латентного тепла из-за дождей или снега и приближенного описания горизонтального переноса тепла и водяного пара. Значения источников в уравнении транспорта для удельной влажности связаны с выпадением осадков, испарением и сублимацией с поверхности [3]. В уравнениях для температуры и удельной влажности учитывается гидродинамический (турбулентный) перенос этих субстанций с ветром, однако его значения в модели не определяются, и должны быть заданы извне. В работе предлагается процедура для исправления этого недостатка.

Считается, что осадки попадают прямо в океан, присутствует или нет морской лед, а испаренная или сублимированная влага исключается из океана или льда соответственно. В задании модели океана в приближении «твердой крышки», применяемом здесь, океан представляется как неисчерпаемый источник пресной воды для льда в океане и воздуха.

Все элементы климатической системы, представленные в модели, могут обмениваться импульсом, теплом и влагой. В комплексной модели применена равномерная по долготе и синусу широты конечно - разностная сетка размером 72 × 72 ячейки с реальным расположением и формой материков [4]. По глубине океан разбит на 8 уровней в виде логарифмической шкалы до 5000 м, аппроксимирующей реальное распределение. Толщина слоев увеличивается с глубиной.

Описание модели атмосферы и основные результаты

Для описания атмосферы, как было указано выше, используется двумерная модель, определяющая зависимость характеристик атмосферы от широты, долготы и изменение во времени. В модели решается осредненное по высоте уравнение для температуры воздуха , учитывающее баланс  солнечного и теплового радиационных потоков, явных (вихревых) потоков тепла с поверхности суши, океана, морского льда, высвобождения латентного тепла вследствие осадков и описания горизонтальных процессов переноса. Члены с источниками в уравнении транспорта и баланса для удельной влажности  определяются осадками P, испарением и сублимацией E с поверхности. Таким образом, уравнения для баланса тепла (связанного с температурой атмосферы) и удельной влажности атмосферы (на единицу площади) имеют следующий вид:

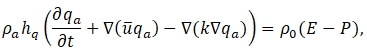      (1)     (2)

где  - высоты атмосферных пограничных слоев для температуры (8,4 км) и влажности (1,8 км) соответственно; ν и κ - коэффициенты турбулентной диффузии для тех же величин;  - плотности воздуха и воды;  - удельная теплоемкость воздуха при постоянном давлении;  - вектор горизонтального ветра (зональная и меридиональная компоненты), t - время.

Двумерное поле скоростей ветра в этой модели атмосферы исходно задается из среднемесячных данных наблюдений. Это означает, что оно не меняется при изменении состояния или параметров климатической системы. Как вариант устранения этого недостатка, здесь вводится процедура определения поля скоростей ветра по полю приземной температуры атмосферы на основе геострофического подхода, учета термальной составляющей ветра и учета механизма трения о подстилающую поверхность. Это позволяет качественно верно описывать поле скоростей ветра в зависимости от характеристик климатической системы.

Для расчета скоростей ветра используем два геострофических соотношения и уравнения гидростатики и состояния идеального газа [5]:

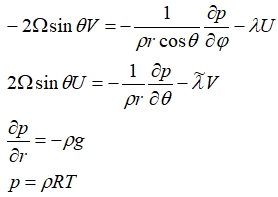
где Ω – угловая скорость вращения Земли, θ – широта, ρ – плотность воздуха, φ – долгота, p – давление, g – ускорение свободного падения, R – универсальная газовая постоянная, T – температура воздуха. Коэффициенты λ и  характеризуют дополнительно введенные процессы трения о подстилающую поверхность, позволяют использовать геострофические соотношения вблизи экватора и подбираются эмпирически. Выразим из уравнения состояния плотность , подставим его в остальные уравнения системы, продифференцируем уравнения для U и V по r.

После интегрирования двух этих уравнений по толщине пограничного слоя атмосферы Н, для стандартной устойчиво стратифицированной атмосферы, и учитывая, что у поверхности земли скорости ветра равны нулю, получим для средних по пограничному слою компонент скоростей окончательные выражения  :

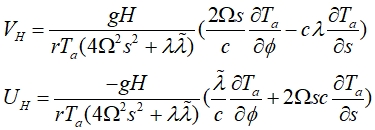
где

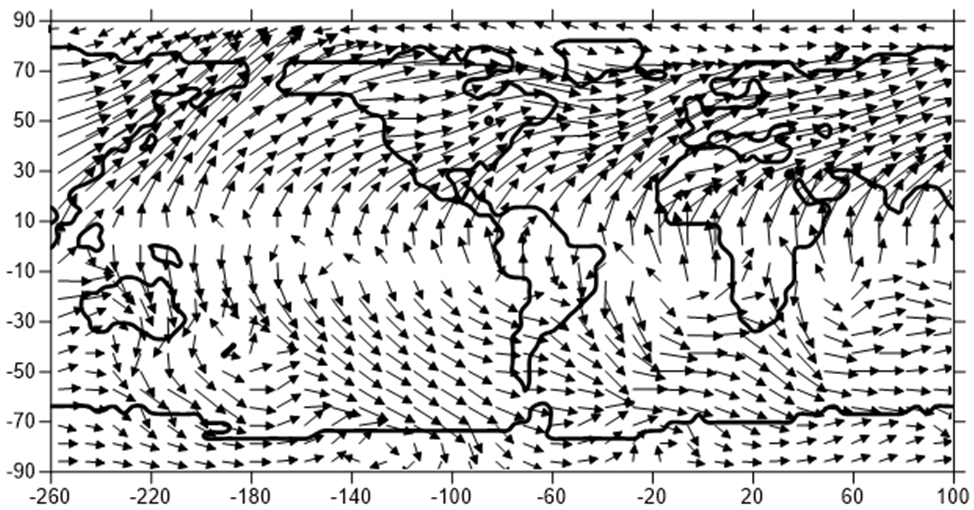
На рисунке 1 показаны рассчитанные в рамках совместной модели скорости ветра для января месяца в приземном слое толщиной 1000 м. Отметим наличие интенсивного западного потока в средних широтах и восточных пассатов в экваториальной области.

Рис. 1 – Глобальное поле скорости ветра в слое атмосферы толщиной 1000 м для января месяца

Примечание: максимальное значение соответствует 4,9 м/с

 

Учет ветра в расчетах приводит к изменению поля температуры атмосферы. Направленные к полюсам потоки вызывают повышение температуры в средних широтах и охлаждение в низких широтах в пределах нескольких градусов [6].

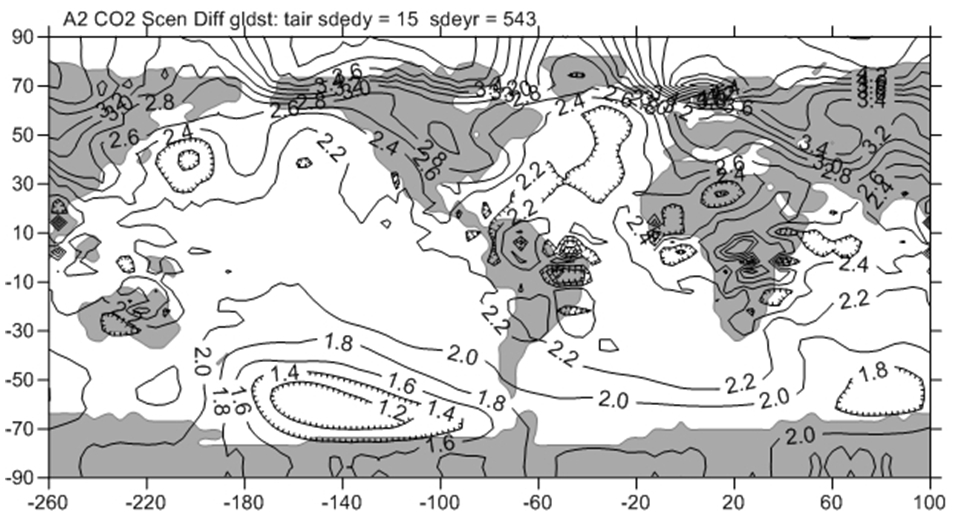
По комплексу моделей проведены расчеты прогнозирования климата до 2100 года на основе сценария РТК8.5 довольно сильного роста СО₂ (концентрация 860 ppm в 2100 г.), предложенном Межправительственной группой экспертов по изменению климата [7] и соответствующему прогнозу экстенсивного развития мировой энергетики. Для него средняя глобальная температура приземного воздуха к концу 21 века выросла на 2.7^ОС, влажность атмосферы – на 11.5%, толщина морского льда уменьшилась - на 25%. Рост приповерхностной температуры воздуха больше над материками, в средних и высоких широтах, достигая величины 5.2^ОС на севере Евразии (см. рисунок 2). В южном полушарии потепление не более 2^ОС [8]. Эти результаты, конечно, нельзя рассматривать как абсолютно достоверный прогноз в силу ограниченности сценария, модели и большого периода прогноза.

Рис. 2 – Изменение температуры (^оС) атмосферы для января, сценарий РТК8.5 повышения CO₂

  Заключение

Описанная процедура позволяет достаточно адекватно описывать поле скоростей ветра в зависимости от состояния климатической системы. Это значительно расширяет возможности применения климатической модели для прогнозирования изменений, для палео реконструкций климата или для исследования климатических режимов, значительно отличающихся от современного [9], [10]. Это продемонстрировано в численном эксперименте прогнозирования климата, как одного из возможных вариантов развития ситуации, при увеличении концентрации СО₂ в соответствии со сценарием РТК8.5 [7].

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Пархоменко В.П. Глобальная модель климата с описанием термохалинной циркуляции Мирового океана / В.П. Пархоменко // Математическое моделирование и численные методы, - 2015. - № 1. – С. 94–108.
2. Marsh R. Development of a fast climate model (C-GOLDSTEIN) for Earth System Science / R. Marsh, N.R. Edwards, J.G. Shepherd // SOC. – 2002. – No.83. – 54 P.
3. Кочергин В.П. Теория и методы расчета океанических течений / В.П. Кочергин. М., Наука. – 1978 - 128 с.
4. Пархоменко В. П. Применение глобальных климатических моделей для исследования климата Земли / В. П. Пархоменко // Труды Института системного анализа Российской академии наук (Труды ИСА РАН). – 2018. – Т. 68, №2. – C. 38–41.
5. Педлоски Дж. Геофизическая гидродинамика, том1 / Дж. Педлоски. - М.: Мир, 1984. - 398 с.
6. Parkhomenko V.P. Modeling of global and regional climate response to solar radiation management / V.P. Parkhomenko // IOP Journal of Physics: Conference Series. – 2018 – V.1141, 012057. – P. 1-5. DOI:10.1088/1742-6596/1141/1/012057
7. IPCC, 2014: Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Core Writing Team, R.K. Pachauri and L.A. Meyer (eds.)]. IPCC, Geneva, Switzerland, 151 p.
8. Пархоменко В.П. Моделирование стабилизации глобального климата управляемыми выбросами стратосферного аэрозоля / В.П. Пархоменко // Математическое моделирование и численные методы, 2014, выпуск 2, 115–126.
9. Пархоменко В.П. Моделирование климатических последствий падения крупного астероида 66 млн лет назад. / В.П. Пархоменко // Математическое моделирование и численные методы. – 2019. – № 2. – С. 68 – 83.
10. Edwards N. R. Uncertainties due to transport-parameter sensitivity in an efficient 3-D ocean-climate model / N. R. Edwards, R. Marsh // Climate Dynamics. – 2005. – V.24. – P. 415-433.

Список литературы на английском языке / References in English

1. Parkhomenko V.P. Global'naja model' klimata s opisaniem termohalinnoj cirkuljacii Mirovogo okeana [A global climate model describing the thermohaline circulation of the World Ocean.] / V.P. Parkhomenko // Matematicheskoe modelirovanie i chislennye metody [Mathematical modeling and numerical methods] - 2015. - № 1. – P. 94–108. [in Russian]
2. Marsh R. Development of a fast climate model (C-GOLDSTEIN) for Earth System Science / R. Marsh, N.R. Edwards, J.G. Shepherd // SOC. – 2002. – No.83. – 54 P.
3. Kochergin V.P. Teorija i metody rascheta okeanicheskih techenij [Theory and methods of ocean flows calculations] / V.P. Kochergin M., Nauka. – 1978 - 128 p. [in Russian]
4. Parkhomenko V.P. Primenenie globalnyh klimaticheskih modelej dlia issledovania klimata Zemli [The application of global climate models for the Earth climate study] / V.P. Parkhomenko // Trudy instituta systemnogo analiza Rossijskoj Akademii Nauk [Proceeding of the Institute for Systems Analysis of the Russian Academy of Science] – 2018. – V. 68, №2. – P. 38–41. [in Russian]
5. Pedlosky J. Geophysical Fluid Dynamics. Springer Science & Business Media, 2012 626 p. DOI: 10.1007/978-1-4612-4650-3
6. Parkhomenko V.P. Modeling of global and regional climate response to solar radiation management / V.P. Parkhomenko // IOP Journal of Physics: Conference Series. – 2018 – V.1141, 012057. – P. 1-5. DOI:10.1088/1742-6596/1141/1/012057
7. IPCC, 2014: Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Core Writing Team, R.K. Pachauri and L.A. Meyer (eds.)]. IPCC, Geneva, Switzerland, 151 p.
8. Parkhomenko V.P. Modelirovanie stabilizacii global'nogo klimata upravljaemymi vybrosami stratosfernogo ajerozolja [Modeling of global climate stabilization by controlled stratospheric aerosol emissions] / V.P. Parkhomenko // Matematicheskoe modelirovanie i chislennye metody [Mathematical modeling and numerical methods] 2014, № 2, P. 115–126. [in Russian]
9. Parkhomenko V.P. Modelirovanie klimaticheskih posledstvij padenija krupnogo asteroida 66 mln let nazad [The climatic consequences modeling of the large asteroid impact 66 million years ago] / V.P. Parkhomenko //Matematicheskoe modelirovanie i chislennye metody [Mathematical modeling and numerical methods – 2019. – № 2. – P. 68 – 83. [in Russian]
10. Edwards N. R. Uncertainties due to transport-parameter sensitivity in an efficient 3-D ocean-climate model / N. R. Edwards, R. Marsh // Climate Dynamics. – 2005. – V.24. – P. 415-433.