КАК ИЗ ТРЕУГОЛЬНИКА ПАСКАЛЯ ИЗВЛЕЧЬ ФОРМУЛЫ ДЛЯ НАХОЖДЕНИЯ ВСЕХ ПРОСТЫХ ЧИСЕЛ
КАК ИЗ ТРЕУГОЛЬНИКА ПАСКАЛЯ ИЗВЛЕЧЬ ФОРМУЛЫ ДЛЯ НАХОЖДЕНИЯ ВСЕХ ПРОСТЫХ ЧИСЕЛ
Научная статья
Щербань В. Л. *
ORCID: 0000-0002-5631-9681,
Центр дополнительного математического образования, Курган, Россия
* Корреспондирующий автор (sherba-q[at]ya.ru)
АннотацияВ настоящем арифметическом исследовании представлены ранее не известные числовые свойства прямоугольного треугольника Паскаля и впервые даны основные результаты нахождения его вещественного дискриминанта. В точности, обнаружены числовые свойства усеченного треугольника Паскаля для отыскивания всех простых чисел. После этого, в конечном итоге, представлены арифметические формулы для прямого нахождения всех простых чисел. Все сказанное и выше перечисленное стало возможным только после успешной расшифровки всего класса числовых таблиц усеченных треугольников в криптографической системе. И далее, после всех достигнутых результатов стал доступным общий метод установления простейших числовых свойств симметричных многочленов степенных сумм. Следует особо отметить, что для обобщения таблиц и бесспорно определить те правила вещественных действий, которые для таблиц должны иметь место, задействованы только рекуррентные числовые ряды.
Ключевые слова: треугольник Паскаля; числа Фибоначчи; простые числа; возвратные (рекуррентные) числовые последовательности.
GETTING FORMULAS FOR THE EXTRACTION OF ALL PRIME NUMBERS FROM THE PASCAL’S TRIANGLE
Research article
Shcherban V. L. *
ORCID: 0000-0002-5631-9681,
Centre for Continuous Mathematical Education, Kurgan, Russia
* Correspondent author (sherba-q[at]ya.ru)
AbstractThe following arithmetic study presents previously unknown numerical properties of the Pascal’s right-angled triangle and gives the main results of finding its real discriminant for the first time. Precisely, the numerical properties of the truncated Pascal’s triangle for the extraction of all prime numbers were discovered. Then, arithmetic formulas are presented for the direct extraction of all prime numbers. All of the above is possible after the entire class of numerical tables of truncated triangles has been successfully decoded in the cryptographic system. After these results had been achieved, the general method of establishing the simplest numerical properties of symmetric polynomials of power sums became available. It should be specially noted that only recurrent numerical series are used for the generalization of tables and precise determination of the rules for these tables.
Keywords: Pascal’s triangle; Fibonacci numbers; prime numbers; recurrent numerical sequences.
ВведениеНиже изложенное арифметическое исследование покажет непосредственную связь чисел «треугольника Паскаля» с симметричными многочленами от (n)-переменных. В точности, найдено числовое решение всего усеченного треугольником Паскаля – это положения (7) и (11). Вслед за этим устанавливаются арифметические формулы для прямого нахождения всех простых чисел (5) и (14), [1]. Логическая структура материала довольно сложна, однако при этом, нет нужды в особых предварительных знаниях, кроме умения осуществлять несложные тождественные преобразования.
Числовые таблицы как предмет рассмотрения
До первоначального знакомства с арифметическими таблицами необходимо обстоятельно ознакомится с простейшими симметричными многочленами степенных сумм [2, С. 20–22]. Для этого необходимы следующие обозначенные многочлены:
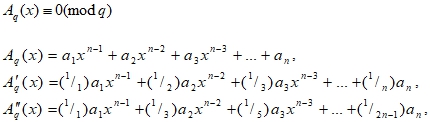 (1)
(1)
Решить арифметическое сравнение (1), это значит найти все значения неизвестного числа (𝑥), ему удовлетворяющие [5]. Два сравнения (или более), которым удовлетворяют одни и те же значения (𝑥), называются равносильными или эквивалентными.
Раньше всего необходимо отметить, что числовые последовательности, в которых каждый член определяется как некоторая функция предыдущих, называются возвратными или рекуррентными [6]. Последовательное нахождение таких чисел определяется при помощи возвратного уравнения.
Представим известную числовую таблицу, которую называют треугольником Паскаля в прямоугольной форме [7]. Суммы чисел, лежащих последовательно на фиксированных восходящих диагоналях, являются рядом Фибоначчи [8]. Ряды чисел, заполняющие последовательно отдельные вертикали треугольника Паскаля называются многоугольными числами. Для нахождения многоугольных чисел служит таблица, в которой каждое число образуется посредством сложения двух чисел, стоящих непосредственно перед ним и над ним, (табл. 1).
Таблица 1 – Многоугольные числа
| 1 2 3 4 5 6 7 8 9 | 1 3 6 10 15 21 28 36 45 | 1 4 10 20 35 56 84 120 165 | 1 5 15 35 70 126 210 330 495 | 1 6 21 56 126 252 462 792 1287 | 1 7 28 84 210 462 924 1716 ....... |
Общий метод построения арифметических таблиц
Вертикальные возвратные (рекуррентные) числовые ряды, для которых осуществимы посредством правил вычислений (сложения, вычитания и числового сравнения) нахождение простейших свойств целых чисел, являются арифметическими таблицами. Основное числовое свойство таблиц размещается посредством действий (операций) над числами, лежащими на фиксированных горизонталях. В таких таблицах отсутствует операция «деления» чисел. По этому, сравнимость чисел (𝑎) и (𝑏) по числовому модулю (q), означает только возможность представить (𝑎) в виде ![]() , где число (t) целое.
, где число (t) целое.
Рассмотрим простейший пример создания арифметической таблицы.
Воспользуемся формулой Варинга [9, С. 53–55] для получения степенной суммы от двух переменных через элементарные многочлены.
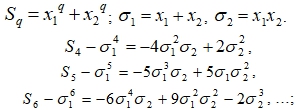
Правая часть последних уравнений позволяет образовать таблицу числовых коэффициентов в абсолютных величинах (табл. 2). После расшифровки последует установление ее главного арифметического свойства. *Метод дешифровки таблицы универсален для всех последующих таких таблиц.
Таблица 2 – Фрагмент коэффициентов степенной суммы от двух переменных
| q | – Y – |
| 4 5 | 4 + 2 5 + 5 |
| 6 7 | 6 + 9 + 2 7 + 14 + 7 |
| 8 9 | 8 + 20 + 16 + 2 9 + 27 + 30 + 9 |
| 10 11 | 10 + 35 + 50 + 25 + 2 11 + 44 + 77 + 55 + 11 |
| 12 13 | 12 + 54 + 112 + 105 + 36 + 2 13 + 65 + 156 + 182 + 91 + 13 |
| 14 15 | 14 + 77 + 210 + 294 + 196 + 49 + 2 15 + 90 + 275 + 450 + 378 + 140 + 15 |
| 16 | …… |
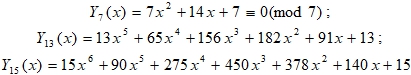 Для всех нечетных чисел (q), многочлен (2) имеет только одно не тривиальное решение:
Для всех нечетных чисел (q), многочлен (2) имеет только одно не тривиальное решение:
Осталось показать, как степенную сумму от двух переменных найти и извлечь из треугольника Паскаля при установленном условии: ![]() , но с помощью формулы (4).
, но с помощью формулы (4).
Расположим числа прямоугольного треугольника Паскаля иным образом. Все числа, лежащие на фиксированных восходящих диагоналях, разместим по отдельным горизонталям. В этом случае, суммы чисел, лежащих последовательно на фиксированных горизонталях, окажутся числами Фибоначчи (табл. 3 – C). Каждую отдельную горизонталь обозначим порядковым номером (q). Определим теоретико-числовые свойства этой таблицы и производной от нее, числовой таблицы (В).
Таблица 3 – Основная таблица числовых сравнений
| q | – В – | – C – |
| 4 5 | 3 + 1 4 + 3 | 1 + 1 1 + 2 |
| 6 7 | 5 + 6 + 1 6 + 10 + 4 | 1 + 3 + 1 1 + 4 + 3 |
| 8 9 | 7 + 15 + 10 + 1 8 + 21 + 20 + 5 | 1 + 5 + 6 + 1 1 + 6 + 10 + 4 |
| 10 11 | 9 + 28 + 35 + 15 + 1 10 + 36 + 56 + 35 + 6 | 1 + 7 + 15 + 10 + 1 1 + 8 + 21 + 20 + 5 |
| 12 13 | 11 + 45 + 84 + 70 + 21 + 1 12 + 55 + 120 + 126 + 56 + 7 | 1 + 9 + 28 + 35 + 15 + 1 1 + 10 + 36 + 56 + 35 + 6 |
| 14 15 | 13 + 66 + 165 + 210 + 126 + 28 + 1 14 + 78 + 220 + 330 + 252 + 84 + 8 | 1 + 11 + 45 + 84 + 70 + 21 + 1 1 + 12 + 55 + 120 + 126 + 56 + 7 |
| 16 17 | 15 + 91 + 286 + 495 + 462 + 210 + 36 + 1 ........................... | 1 + 13 + 66 + 165 + 210 + 126 + 28 + 1 .............................. |
Горизонтальные числа, исключая порядковые номера (q), станем кодировать уже известным способом (табл. 3). В точности, таблица (В):
![]()
Число (q) – обозначенный порядковый номер многочлена.
Число (n) – обозначенное количество чисел (𝑏), стоящих на фиксированных горизонталях.
Соответственно, таблица (С):
![]()
![]() ; Число (𝚔), является числом Фибоначчи.
; Число (𝚔), является числом Фибоначчи.
Зафиксируем непосредственную связь между числовыми многочленами:
![]() (4)
(4)
Отметим только простейшие числовые свойства таблиц (В) и (С).
Система сравнений многочленов: ![]() , равносильна для всех простых чисел (q). Доказательством этого утверждения является условие формул (3) и (4).
, равносильна для всех простых чисел (q). Доказательством этого утверждения является условие формул (3) и (4).
Соответствующие примеры.
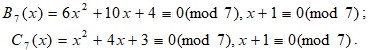
Система сравнений: ![]() , равносильна для всех простых чисел (q). Пример:
, равносильна для всех простых чисел (q). Пример:
После всего выше подтвержденного необходимо обратить внимание на следующий многочлен:
![]()
Этот многочлен имеет все целые числовые коэффициенты только тогда, когда (q) – число простое, (табл. 3 – C) или (табл. 6).
Статус данного арифметического положения – формула, служащая для нахождения всех простых чисел (то есть, не способ для тестирования). Плюс, несложное числовое свойство алгоритма представленной формулы, допускает ее компьютерную реализацию.
В точности, ![]() – конкретное число Фибоначчи. Примеры:
– конкретное число Фибоначчи. Примеры:
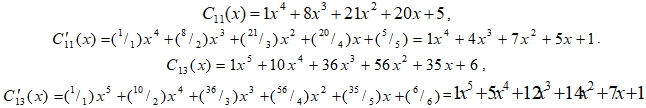
Для краткого доказательства этого утверждения достаточно закрепить простые или составные числа в две очевидные формулы: ![]() . Затем подвергнуть анализу степенную сумму в качестве системы. Полное доказательство не приводиться ввиду его громоздкости и фактической схожестью с доказательством для следующего многочлена такого же типа:
. Затем подвергнуть анализу степенную сумму в качестве системы. Полное доказательство не приводиться ввиду его громоздкости и фактической схожестью с доказательством для следующего многочлена такого же типа: ![]() – (14).
– (14).
Усеченный треугольник Паскаля и его дешифровка
Для нечетных чисел (q) разложим по формуле Варинга степенную сумму от трех переменных такого вида:
![]() (6)
(6)
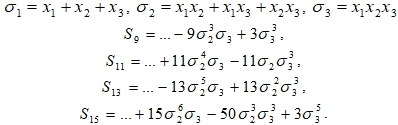
Правая часть последних уравнений позволяет создать таблицу числовых коэффициентов в абсолютных величинах (табл. 4 – G) и производную от нее таблицу (U). После расшифровки установим основные их арифметические свойства.
Таблица 4 – Фрагмент коэффициентов степенной суммы от трех переменных
| q | – U – | – G – |
| 9 11 13 | 24 + 3 35 + 14 48 + 40 | 9 + 3 11 + 11 13 + 26 |
| 15 17 19 | 63 + 90 + 3 80 + 175 + 20 99 + 308 + 77 | 15 + 50 + 3 17 + 85 + 17 19 + 133 + 57 |
| 21 23 25 | 120 + 504 + 224 + 3 143 + 780 + 546 + 26 168 + 1155 + 1176 + 126 | 21 + 196 + 147 + 3 23 + 276 + 322 + 23 25 + 375 + 630 + 100 |
| 27 29 31 | 195 + 1650 + 2310 + 450 + 3 224 + 2288 + 4224 + 1320 + 32 255 + 3094 + 7293 + 3366 + 187 | 27 + 495 + 1134 + 324 + 3 29 + 638 + 1914 + 870 + 29 31 + 806 + 3069 + 2046 + 155 |
| 33 | ..................... | .................... |
Горизонтальные числа, исключая порядковые номера (q), надлежит кодировать следующим способом (табл. 4): ![]() . Примеры:
. Примеры:
![]()
Перечислим только бесспорные (стало быть – невозможно опровергнуть) числовые свойства указанных таблиц.
![]() (7)
(7)
Примеры: ![]() .
.
Система сравнений: ![]() , равносильна для всех простых чисел (q).
, равносильна для всех простых чисел (q).
Система сравнений: ![]() , равносильна для всех простых чисел (q). Например:
, равносильна для всех простых чисел (q). Например:
![]()
Далее покажем, как степенную сумму (6) обнаружить и извлечь из треугольника Паскаля при установленном условии: ![]() , но с помощью формул (8).
, но с помощью формул (8).
Рассмотрим ряды чисел, заполняющие отдельные вертикали прямоугольного треугольника Паскаля (табл. 3 – C). Только теперь повторно выстраивается подобный числовой треугольник, но в котором отсутствуют все вертикальные числовые ряды под четными номерами, а каждая последующая числовая вертикаль поднимается вверх на одну позицию предыдущей порядковой горизонтали. В полученном усеченном треугольнике (F) и производном от него треугольника (E), каждая фиксированная горизонталь обозначена порядковыми нечетными номерами (q), (табл. 5). Из многих числовых свойств указанных таблиц выберем только несколько основных.
Предварительно зафиксируем два очевидных уравнения:
![]() (8)
(8)
Таблица 5 – Усеченный треугольник Паскаля (F)
| q | – E – | – F – |
| 9 11 13 | 4 + 1 5 + 4 6 + 10 | 1 + 1 1 + 3 1 + 6 |
| 15 17 19 | 7 + 20 + 1 8 + 35 + 6 9 + 56 + 21 | 1 + 10 + 1 1 + 15 + 5 1 + 21 + 15 |
| 21 23 25 | 10 + 84 + 56 + 1 11 + 120 + 126 + 8 12 + 165 + 252 + 36 | 1 + 28 + 35 + 1 1 + 36 + 70 + 7 1 + 45 + 126 + 28 |
| 27 29 31 | 13 + 220 + 462 + 120 + 1 14 + 286 + 792 + 330 + 10 15 + 364 + 1287 + 792 + 55 | 1 + 55 + 210 + 84 + 1 1 + 66 + 330 + 210 + 9 1 + 78 + 495 + 462 + 45 |
| 33 35 37 | 16 + 455 + 2002 + 1716 + 220 + 1 17 + 560 + 3003 + 3432 + 715 + 12 18 + 680 + 4368 + 6435 + 2002 + 78 | 1 + 91 + 715 + 924 + 165 + 1 1 + 105 + 1001 + 1716 + 495 + 11 1 + 120 + 1365 + 3003 + 1287 + 66 |
| 39 | ..................... | ....................... |
Горизонтальные числа, исключая порядковые номера (q), следует кодировать, в том числе и способом обратных арифметических прогрессий (1). Примеры:
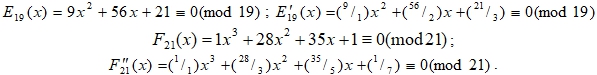
Отметим только необходимые свойства таблиц (E) и (F), для чисел (q > 13) – (табл. 5).
Система сравнений: ![]() , равносильна для всех простых чисел (q). Примеры:
, равносильна для всех простых чисел (q). Примеры: ![]() .
.
Система сравнений: ![]() , равносильна только тогда, когда (q) – число простое. Примеры:
, равносильна только тогда, когда (q) – число простое. Примеры:
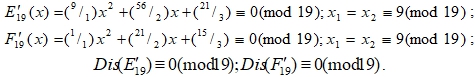
Система сравнений: ![]() , равносильна для всех простых чисел (q). Примеры:
, равносильна для всех простых чисел (q). Примеры: ![]() .
.
Дальше будут рассмотрены только арифметические свойства треугольника (F).
Если число (q) – составное, тогда при условии (7) и (11):
![]()
![]() (9)
(9)
Если число (q) – простое, тогда и лишь только :
![]() (10)
(10)
Примеры:
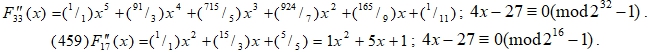
Для чисел (q > 13) арифметическая система (6) и (8) эквивалентна при установленном условии:
![]() (11)
(11)
Первый пример:
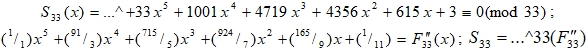
Второй пример:
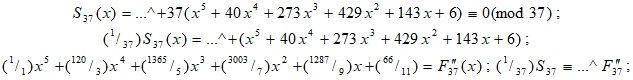
Продолжение анализа числовых свойств треугольника (F).
Если число (q) – простое, тогда сравнение: ![]() , имеет столько решений, какова его степень. Примеры:
, имеет столько решений, какова его степень. Примеры: ![]() ;
;
Система сравнений: ![]() , равносильна для всех простых чисел (q). Примеры:
, равносильна для всех простых чисел (q). Примеры:
Система сравнений:
![]() (12)
(12)
равносильна только тогда, когда число (q) – простое. Примеры:
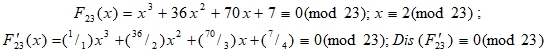
Далее, система сравнений:
![]() (13)
(13)
равносильна только тогда, когда числа (q) и (h) – взаимно простые. Примеры:
![]()
Числа Фибоначчи, первые изъяты в явной форме из треугольника Паскаля и считаются по этому, первой по счету числовой возвратной последовательностью [10, С. 11]. Воспроизведенные формулы Виета [11], по аналогии, предлагают второй по счету числовой ряд после чисел Фибоначчи, и который имеет возвратное уравнение: ![]() . Далее, следует по счету третий ряд чисел:
. Далее, следует по счету третий ряд чисел: ![]() , который распадается на два числовых ряда – по четными и нечетными порядковыми номерами, и имеющие равные возвратные уравнения (табл. 5):
, который распадается на два числовых ряда – по четными и нечетными порядковыми номерами, и имеющие равные возвратные уравнения (табл. 5):
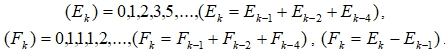
Проверочное числовое сравнение для простых чисел: ![]() . Числа (E𝚔) и (F𝚔) – сумма чисел лежащих на фиксированных горизонталях обозначенными номерами (q). Пример:
. Числа (E𝚔) и (F𝚔) – сумма чисел лежащих на фиксированных горизонталях обозначенными номерами (q). Пример: ![]() .
.
После исследования многочлена (5), приступаем к изучению следующего многочлена:
![]() (14)
(14)
Этот многочлен имеет все целые числовые коэффициенты только тогда, когда (q) – число простое, (табл. 5 – F) или (табл. 7). Примеры:
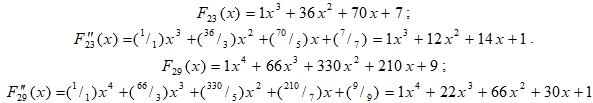
Решающим доказательством данного утверждения, является положение (11), при котором система сравнений (9) и (10), не эквивалентна без установочного условия: ![]() . Или в точности, многочлен:
. Или в точности, многочлен: ![]() , если число (q) – простое (16). Подтвердим это еще и следующим положением. Системы сравнений (12) и (13) – не эквивалентны. Доказательство размещено в пятом разделе-параграфе.
, если число (q) – простое (16). Подтвердим это еще и следующим положением. Системы сравнений (12) и (13) – не эквивалентны. Доказательство размещено в пятом разделе-параграфе.
Нахождение всех простых чисел с помощью формул (5) и (14)
Таблицы Паскаля служат, в том числе, и для создания заранее определенного алгоритма арифметически-логического устройства {АЛУ}, выполняющего арифметические и логические операции. Смотрим таблицу числовых сравнений, (табл. 3 – C). Эта таблица в полном формате на этом месте – (табл. 6).
Выбирается первый необязательный порядковый многочлен:
Число (q) является порядковым номером многочлена. Число (n) равно количеству чисел ![]() , стоящих на фиксированных горизонталях. Например:
, стоящих на фиксированных горизонталях. Например:
Таблица 6 – Треугольник Паскаля (C)
| №q | (C) | |
| 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | 1 + 3 + 1 1 + 4 + 3 1 + 5 + 6 + 1 1 + 6 + 10 + 4 1 + 7 + 15 + 10 + 1 1 + 8 + 21 + 20 + 5 1 + 9 + 28 + 35 + 15 + 1 1 + 10 + 36 + 56 + 35 + 6 1 + 11 + 45 + 84 +70 + 21 + 1 1 + 12 + 55 + 120 +126 + 56 + 7 1 + 13 + 66 + 165 + 210 + 126 + 28 + 1 1 + 14 + 78 + 220 + 330 + 252 + 84 + 8 1 + 15 + 91 + 286 + 495 + 462 + 210 + 36 + 1 1 + 16 + 105 + 364 + 715 + 792 + 462 +120 + 9 1 + 17 + 120 + 455 + 1001 + 1287 + 924 +330 + 45 + 1 1 + 18 + 136 + 560 + 1365 + 2002 + 1716 +792 + 165 + 10 1 + 19 + 153 + 680 + 1820 + 3003 + 3003 + 1716 + 495 +55 +1 1 + 20 + 171 + 816 + 2380 + 4368 + 5005 + 3432 + 1287 +220 + 11 ............................................................. | |
Создается второй многочлен (5) – дискриминантный, (табл. 6):
![]()
Этот многочлен имеет все целые числовые коэффициенты только тогда, когда (q) – число простое. Например:
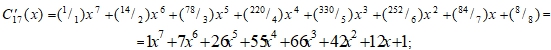
Далее, смотрим усеченный треугольник Паскаля (табл. 5 – F). Эта таблица в полном формате на этом месте (табл. 7).
Выбирается первый необязательный порядковый многочлен:
Число (q) является порядковым номером многочлена.
Число (n) равно количеству чисел ![]() , стоящих на фиксированных горизонталях.
, стоящих на фиксированных горизонталях.
Например: ![]() ;
;
Таблица 7 – Арифметический треугольник (F)
| №q | (F) | |
| 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 | 1 + 10 + 1 1 + 15 + 5 1 + 21 + 15 1 + 28 + 35+ 1 1 + 36 + 70+ 7 1 + 45 + 126 + 28 1 + 55 + 210 + 84+ 1 1 + 66 + 330 + 210+ 9 1 + 78 + 495 + 462+ 45 1 + 91 + 715 + 924+ 165+ 1 1 + 105 + 1001 + 1716 + 495+ 11 1 + 120 + 1365 + 3003 + 1287+ 66 1 + 136 + 1820 + 5005 + 3003+ 286+ 1 1 + 153 + 2380 + 8008 + 6435+ 1001+ 13 1 + 171 + 3060 + 12376 + 12870 + 3003+ 91 1 + 190 + 3876 + 18564 + 24310 + 8008+ 455+ 1 1 + 210 + 4845 + 27132 + 43758 + 19448 + 1820 + 15 1 + 231 + 5985 + 38760 + 75582 + 43758 + 6188 + 120 1 + 253 + 7315 + 54264 + 125970 + 92378 + 18564 + 680 + 1 1 + 276 + 8855 + 74613 + 203490 + 184756 + 50388 + 3060 + 17 ............................................................. | |
Создается второй многочлен (14) – дискриминантный, (табл. 7):
![]()
Этот многочлен имеет все целые числовые коэффициенты только тогда, когда (q) – число простое. Например:
![]()
Этот результат является следствием доказанного утверждения: ![]() , если (q) – простое число, (13) и (16). Это положение, по-другому подтверждается и так. Арифметический треугольник (F) допускает только два не тривиальных решений (9) и (10). 5. Как доказываются числовые свойства арифметических треугольников
, если (q) – простое число, (13) и (16). Это положение, по-другому подтверждается и так. Арифметический треугольник (F) допускает только два не тривиальных решений (9) и (10). 5. Как доказываются числовые свойства арифметических треугольников
Предлагается степенная сумма (6), которая разлагается по формуле Варинга на элементарные многочлены и образует систему с возвратным уравнением (в общем виде – числовым сравнением):
![]()
С помощью биномиальных коэффициентов Ньютона и многоугольных чисел треугольника Паскаля (табл. 1), устанавливаются очевидные уравнения и сравнения (табл. 5):
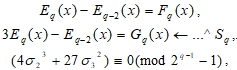
Вслед за этим открываем сущность, специально предназначенного метода «от противного», при котором «доказывание» некоторого свойства треугольника Паскаля – суждения (тезиса доказательства), осуществляется через опровержение отрицания этого суждения — антитезиса. Этот способ доказательства основывается на истинности закона двойного отрицания в классической логике.
Например, подробно исследуем следующее положение.
Предположим, что для какого-то многочлена (9) или (14), имеется конкретное числовое сравнение: ![]() , число (q) – простое.
, число (q) – простое.
Вследствие этого системы сравнений (12) и (13), станут эквивалентными.
Или в точности (1):
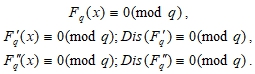
В этом случае, после несложных вычислений, извлекается утверждение: ![]() , но которое невозможно. В самом деле, тогда будут иметь место последующие арифметические действия:
, но которое невозможно. В самом деле, тогда будут иметь место последующие арифметические действия:
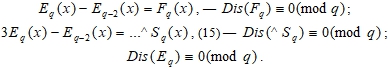
Вследствие чего, станут по – тройне равносильны все последующие системы сравнений:
![]()
Чего быть не может, так как противоречит всем заявленным условиям, в том числе и установкам (15) и (17). Следовательно, если число (q) – простое, тогда многочлен:
![]() (16)
(16)
Таким образом, главное арифметическое свойство треугольника (F) для нахождения всех простых чисел — доказано, (табл. 7).
Разъяснение:![]()
![]() — каждый многочлен выше обозначенного типа:
— каждый многочлен выше обозначенного типа:
(k) – второй числовой элемент обратной арифметической прогрессии, в которой каждый следующий элемент равен предыдущему, увеличенному на фиксированное для прогрессии число (k – 1), [12].
Вновь предположим, что для какого-то многочлена (12) имеется конкретное числовое сравнение: ![]() , число (q) является составным. Тогда системы сравнений (12) и (13), снова станут равносильными, что опровергнуто выше показанным доказательством. Стало быть, системы сравнений (12) и (13) не эквивалентные.
, число (q) является составным. Тогда системы сравнений (12) и (13), снова станут равносильными, что опровергнуто выше показанным доказательством. Стало быть, системы сравнений (12) и (13) не эквивалентные.
Осталось отметить, что возвратное арифметическое сравнение степенной суммы от двух переменных: ![]() , и степенной суммы от трех переменных:
, и степенной суммы от трех переменных:
— имеют особый статус. Они взяты в зашифрованном виде из таблиц (табл. 2) и (табл. 4), поэтому бесспорны по определению.
Примечание:
Заметим, что положение (6), легко конвертируется в другое доказанное утверждение —![]() . При этом показатели
. При этом показатели ![]() должны удовлетворять неким условиям [13, С. 20–21].
должны удовлетворять неким условиям [13, С. 20–21].
Заключение
Краткое арифметическое определение дискриминанта кубического трехчлена известно – два вещественных корня такого многочлена равны (сравнимы). Неизвестно понятие дискриминанта степенной суммы от трех переменных [14]. Отчего, впервые были предоставлены только числовые выкладки их конкретного измерения. Следом за этим отметим, что полученные арифметические треугольники оказались усеченными то и порядковые числа рассматривались, например (q > 13), для нахождения соответствующих числовых дискриминантов.
Таблицы степенных сумм от четырех переменных составляются так. Все вертикальные числовые ряды последовательно делятся на три части и группируются следующим образом (табл. 3). В первую группу входят первый, четвертый, седьмой и так далее по счету вертикальные ряды чисел. Во вторую группу входят второй, пятый, восьмой и так далее по счету вертикальные ряды чисел. В третью группу входят третий, шестой, девятый и так далее по счету вертикальные ряды чисел. Для составления одной сводной таблицы, каждая последующая числовая вертикаль поднимается вверх на две позиции предыдущей порядковой горизонтали.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Воронин С.М. Простые числа / С.М. Воронин. – М.: Знание, 1978. – 96 с.
- Прасолов В.В. Многочлены / В.В. Прасолов. – М.: МЦНМО, 2001. - 336 с.
- Батхин А.Б. Вычисление обобщённого дискриминанта вещественного многочлена/ А.Б. Батхин. // Препринты ИПМ им. М. В. Келдыша. – 2017. - Т. 1, № 88.
- Калинина Е.А. Теория исключения / Е.А. Калинина, Ю.А. Утешев. – СПбГУ: НИИ химии, 2002. - 72 с.
- Гельфонд А.О. Решение уравнений в целых числах / А.О. Гельфонд. – М.: Наука, 1978. - 63 с.
- Маркушевич А.И. Возвратные последовательности / А.И. Маркушевич. – М.: Наука, 1983. - 49 с.
- Успенский В.А. Треугольник Паскаля/ В.А. Успенский. – М.: Наука, 1979. - 47 с.
- Воробьев Н.Н. Числа Фибоначчи / Н.Н. Воробьев. – М.: Наука, 1992. - 190 с.
- Болтянский В.Г. Симметрия в алгебре / В.Г. Болтянский, Н.Я. Виленкин. – М.: МЦНМО, 2002. - 240 с.
- Щербань В.Л. Сверхбыстрое нахождение всех простых чисел: формула [Электронный ресурс] / В.Л. Щербань // Бюллетень науки и практики. – 2017. – № 9 (22). – С. 8-13. – URL: http://www.bulletennauki.com/levchenko (дата обращения 10.01.2020).
- Винберг Э.Б. Алгебра многочленов / Э.Б. Винберг. – М: Просвещение, 1980. - 110с.
- Выгодский М.Я. Справочник по элементарной математике / М.Я. Выгодский. – М.: Гостехиздат, 1954. - 412 с.
- Постников М.М. Введение в теорию алгебраических чисел / М.М. Постников. – М.: Наука, 1982. - 239 с.
- Александрова П.С. Энциклопедия элементарной математики / П.С. Александрова, А.И. Маркушевич, А.Я. Хинчин. – М.-Л.: ГТТИ, 1951. - 448 с.
Список литературы на английском языке / References in English*
- Voronin S.M. Prostye chisla [The Prime numbers] / S.M. Voronin. – M.: Znanie, 1978. – 96 p. [in Russian]
- Prasolov V.V. Mnogochleny [Polynomials] / V.V. Prasolov. – M.: MCNMO, 2001. – 336 p. [in Russian]
- Bathin A.B. Vychislenie obobshchyonnogo diskriminanta veshchestvennogo mnogochlena[Calculating the generalized discriminant of a real polynomial] / A.B. Bathin., – М.: Preprinty IPM im. M. V. Keldysha, 2017. no. 88, 40 p. [in Russian]
- Kalinina E.A. Teoriya isklyucheniya [Exclusion theory] / E.A. Kalinina, A.Yu. Uteshev. – Petersburg: Institute of chemistry., 2002. – 72 p. [in Russian]
- Gel'fond A.O. Reshenie uravnenij v celyh chislah [The solution of equations in integers] / A.O. Gel'fond. – M.: Nauka, 1978. – 63 p. [in Russian]
- Markushevich A.I. Vozvratnye posledovatel'nosti [Recurring sequence] / A.I. Markushevich. – M.: Nauka, 1983. – 49 p. [in Russian]
- Uspenskij V.A. Treugol'nik Paskalya [Pascal triangle] / V.A. Uspenskij. – M.: Nauka, 1979. – 47 p. [in Russian]
- Vorob'ev N.N. Chisla Fibonachchi [Fibonacci number] / N.N. Vorob'ev. – M.: Nauka, 1992. – 190 p. [in Russian]
- Boltyanskij V.G. Simmetriya v algebra [Symmetry in algebra] / V.G. Boltyanskij, N.Yа. Vilenkin. – M.: MCNMO, 2002. – 240 p. [in Russian]
- Shcherban V.L. Sverhbystroe nahozhdenie vsekh prostyh chisel: formula [Super-fast finding of all Prime numbers], [Electronic resource] / V.L. Shcherban // Bulletin of Science and Practice. – 2017. – N9 (22). – Р. 8-13. – URL: http://www.bulletennauki.com/levchenko (accessed: 10.01.2020). [in Russian]
- Vinberg E.B. Algebra mnogochlenov [Algebra of polynomials] / E.B. Vinberg. – M: Prosveshchenie, 1980. – 110 p. [in Russian]
- Vygodskij M.Ya. Spravochnik po elementarnoj matematike [Handbook of elementary mathematics] / M.Ya. Vygodskij. – M.: Gostekhizdat, 1954. – 412 p. [in Russian]
- Postnikov M.M. Vvedenie v teoriyu algebraicheskih chisel [Introduction to the theory of algebraic numbers] / M.M. Postnikov. – M.: Nauka, 1982. – 239 p. [in Russian]
- Aleksandrova P.S. Enciklopediya elementarnoj matematiki [Encyclopedia of elementary mathematics] / P.S. Aleksandrova, A.I. Markushevich, A.Yа. Hinchin. – M.-L.: GTTI, 1951. – 448 p. [in Russian]
