ИССЛЕДОВАНИЕ МОНОТОНИЗИРОВАННЫХ РАЗНОСТНЫХ СХЕМ
ИССЛЕДОВАНИЕ МОНОТОНИЗИРОВАННЫХ РАЗНОСТНЫХ СХЕМ
Научная статья
Трощиев Ю. В. *
ORCID: 0000-0001-6805-7001,
МГУ, Москва, Россия
* Корреспондирующий автор (yuvt[at]yandex.ru)
АннотацияВ статье исследуются возможности практического применения ранее предложенных автором монотонизированных разностных схем. Выведено условие монотонности для немонотонизированной схемы. Показано, что монотонизированные схемы могут как совсем удалять осцилляции, так и уменьшать амплитуду колебаний без изменения условия монотонности. Доказаны некоторые свойства монотонизированных схем. Приведены примеры монотонизирующих операторов. Построена удобная конструкция для решения задач, зависящих от времени. Результаты могут быть обобщены и для более широкого множества задач.
Ключевые слова: разностные схемы, монотонность, аппроксимация, устойчивость, сходимость.
STUDY OF MONOTONIZED DIFFERENCE SCHEMES
Research article
Troshchiev Yu.V. *
ORCID: 0000-0001-6805-7001,
Moscow State University, Moscow, Russia
* Corresponding author (yuvt[at]yandex.ru)
AbstractThe paper considers the possibilities of the practical application of monotonized difference schemes previously proposed by the author. The author introduced the monotonicity condition for a nonmonotonic scheme. It is shown that monotonized schemes can both completely remove oscillations and reduce the amplitude of oscillations without changing the condition of monotony, besides some properties of monotonized schemes are proved. The author provides examples of monotonizing operators and develops a convenient design for solving time-dependent tasks. The results can be generalized to a wider variety of tasks.
Keywords: difference schemes, monotonicity, approximation, stability, convergence.
ВведениеПри решении дифференциальных уравнений с помощью разностных схем довольно часто появляются осцилляции решений от точки к точке сетки [1], [2]. Это явление вызывается свойствами схемы и называется немонотонностью. Если решается задача, имеющая физический смысл, то это явление также называют нефизическими осцилляциями. Наиболее универсальный метод избавиться от этих осцилляций – сглаживание полученных решений [1], но при этом обычно нарушаются законы сохранения и быстро нивелируется влияние начальных условий. Возможно и построение монотонных схем, например, [3], но универсального метода, видимо, нет.
В работах [4], [5], [6] автором была предложена алгебраическая конструкция, с помощью которой можно улучшать свойства монотонности существующих разностных схем. Идея состоит в том, чтобы встраивать в схемы монотонизирующие операторы. Если задача имеет физический смысл, то и законы сохранения при таком встраивании не нарушаются. В результате появляется возможность в несколько раз (в 3-5 раз) увеличить шаг сетки, что для двумерных и трехмерных задач приводит к многократному уменьшению времени счета и требуемой оперативной памяти. При этом немонотонность сохраняется «внутри» разностной схемы: у производных решения и у вспомогательного решения (если осцилляций нет и там, то можно решать по немонотонизированной схеме). Таким образом, метод несколько расширяет круг задач, которые возможно решить на имеющемся компьютере.
В данной работе рассматриваются практические принципы применения метода, т.е. методы выбора шага сетки и монотонизирующих операторов. Хотя основное внимание уделяется линейному одномерному уравнению и одной разностной схеме для этого уравнения, но область применения этих принципов существенно более широкая. Условие монотонности таким же способом можно выводить и для других разностных схем. Если уравнение нелинейное, то отображение можно разложить по формуле Тейлора с помощью производных Фреше и проверять условие монотонности для линеаризованного уравнения. Если уравнение многомерное, задачу часто можно свести к множеству одномерных задач методами расщепления.
Линейное уравнение
В дальнейшем будет неоднократно рассматриваться уравнение вида
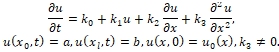 (1)
Все числа в (1) действительные. Если рассматривать стационарное уравнение
(1)
Все числа в (1) действительные. Если рассматривать стационарное уравнение 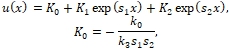 (2)
Где
(2)
Где
В стационарном случае можно без ограничения общности считать ![]() .
.
Будем отличать разностное решение от непрерывного по наличию индексов. Т.е. непрерывное решение ![]() , а разностное
, а разностное ![]() . Запишем для уравнения (1) разностную схему:
. Запишем для уравнения (1) разностную схему:
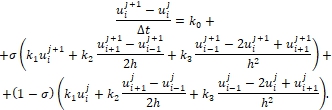 (5)
(5)
Такая схема, видимо, может считаться наиболее естественной в смысле записи аппроксимаций дифференциальных операторов. Здесь ![]() , соответствует значению функции в точке
, соответствует значению функции в точке ![]() граничные значения
граничные значения ![]() будем также обозначать
будем также обозначать ![]() . Схема имеет второй порядок аппроксимации по x. При
. Схема имеет второй порядок аппроксимации по x. При ![]() аппроксимация по времени первого порядка, но вычислительный алгоритм заметно упрощается. При
аппроксимация по времени первого порядка, но вычислительный алгоритм заметно упрощается. При ![]() аппроксимация по времени первого порядка, но схема абсолютно устойчива. При
аппроксимация по времени первого порядка, но схема абсолютно устойчива. При ![]() аппроксимация по времени второго порядка.
аппроксимация по времени второго порядка.
Для стационарного случая соответствующая разностная схема выглядит так:
![]() (6)
(6)
Рассмотрим на примере этой схемы немонотонность по пространству. На рис. 1 показаны решения для двух различных наборов значений параметров.
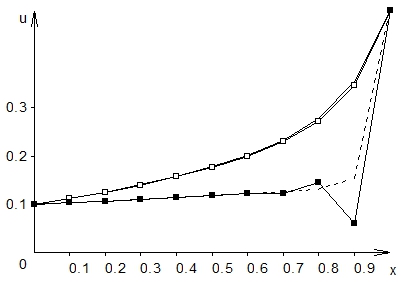
Рис. 1 – Решения по схеме (6). ![]() . Сплошная линия соединяет значения точного решения в узлах сетки, прозрачные маркеры – решение по схеме. б)
. Сплошная линия соединяет значения точного решения в узлах сетки, прозрачные маркеры – решение по схеме. б) ![]() . Пунктир соединяет значения точного решения в узлах сетки, черные маркеры – решение по схеме
. Пунктир соединяет значения точного решения в узлах сетки, черные маркеры – решение по схеме
Вариант а) представляет адекватное приближение точного решения сеточным, а в варианте б) у правой границы видны осцилляции сеточного решения. Это называется немонотонностью. Если бы мы решали физическую задачу, то сеточное решение в этом случае было бы нефизичным. При измельчении шага сетки сеточное решение будет сходиться к точному, и немонотонность исчезнет. Но измельчение шага сетки во многих случаях неприемлемо, особенно для многомерных задач, так как возрастает время счета, требуется значительно больше оперативной памяти. И вообще не очень естественно задавать решение с шагом, в несколько раз меньшим, чем реально необходимо.
Более целесообразно монотонизировать разностную схему. Слово монотонизация подразумевает, что монотонизированная схема строится на основе существующей, но обладает более хорошими свойствами монотонности решений. Если в исходной схеме зааппроксимированы физические законы сохранения, то они окажутся заппроксимированы и в монотонизированной схеме. В отличие, например, от сглаживания решений. С практической точки зрения монотонизация позволяет внести в уже написанную компьютерную программу для разностной схемы небольшие изменения и получить программу с более хорошей разностной схемой.
В этой статье выводятся условия монотонности решений для стационарных задач. В соответствии с [7] их можно назвать условиями практической устойчивости, но там практической неустойчивостью называется бесконечное нарастание каких-нибудь компоненты решения при решении нестационарных задач. А для стационарных задач бесконечного нарастания нет. Кроме того, и при счете по времени бесконечного нарастания может не быть, а по пространству сеточное решение может все же оказаться немонотонным.
Условия монотонности для линейного уравнения
Сначала выведем условие монотонности для схемы (6). Для этого ее удобнее записать в виде
![]() (7)
(7)
где ![]() .
.
Для уравнения (7) выполнены соотношения
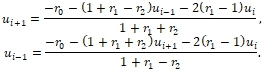 (8)
При достаточно малых значениях h величинами
(8)
При достаточно малых значениях h величинами 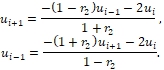 (9)
(9)
Если бы значение h можно было менять непрерывно, то появление максимума или минимума на разностном решении происходило бы через равенство значений в соседних узлах сетки. Значение ![]() равно
равно ![]() . Т.е. решение будет монотонным, если
. Т.е. решение будет монотонным, если ![]() . Возвращаясь к переменным
. Возвращаясь к переменным ![]() получаем приблизительное достаточное условие монотонности:
получаем приблизительное достаточное условие монотонности:
При достаточно малых значениях h все неравенства будут выполнены. Последнее неравенство системы (10) предполагает, что при решении, близком к нулю, близкие к нулю колебания несущественны. Подразумевается нуль в вычислительном смысле, например, когда точность сходимости каких-нибудь итераций сравнима величиной решения, или решение почти равно нулю по физическому смыслу решаемой задачи.
Метод монотонизации
Если получено немонотонное решение, а возможности измельчить шаг сетки нет, то часто решение сглаживается [1]. Но сглаживание почти всегда нарушает какие-нибудь законы сохранения. Кроме того, для задач, решаемых по времени, оно довольно быстро уничтожает влияние начальных условий.
В работах [4], [5], [6] был предложен метод встраивания монотонизирующих операторов в разностные схемы. Монотонизирующие операторы можно было бы назвать и сглаживающими, но сглаживание по смыслу относится к решению, а монотонизирующие операторы улучшают свойства монотонности разностных схем. Кроме того, для встраивания их обычно лучше представить именно в виде операторов для выполнения с ними различных алгебраических действий. Метод состоит в следующем.
Пустьразностная схема. Rn – действительное -мерное пространство. Схема может быть нелинейной, многомерной по пространству и в каждой точке сетки могут быть заданы как одна, так и несколько переменных. Будем считать, что в аппроксимируемое уравнение входят производные порядка не более, чем , причем производная порядка входит существенно. Тогда разностную схему (11) можно представить в виде
![]() (12)
(12)
где Di – оператор вычисления -й производной. Пусть M - монотонизирующий оператор, тогда монотонизированная схема имеет вид
![]() (13)
(13)
Здесь y – решение, v – вспомогательная функция. Первое уравнение в (13) будем называть вспомогательной разностной схемой. Под улучшением свойств монотонности будем понимать, как получение монотонного решения, так и уменьшение амплитуды колебаний.
Монотонизирующий оператор может быть, как вырожденным, так и невырожденным. Если он невырожден, то схему (13) можно записать в виде
![]() (14)
(14)
Порядок аппроксимации схем (13), (14) больше или равен меньшему из двух чисел: порядок аппроксимации схемы (12) и порядок аппроксимации монотонизирующего оператора.
Утверждение 1. Пусть схема (12) линейна и обладает аппроксимацией. Если существует ![]() , при котором для любого положительного
, при котором для любого положительного ![]() оператор
оператор ![]() невырожден и монотонизирующий оператор обладает аппроксимацией, то решения схем (13) и (14) сходятся к решению непрерывной задачи. В случае многомерных схем это максимум из шагов по каждому из направлений.
невырожден и монотонизирующий оператор обладает аппроксимацией, то решения схем (13) и (14) сходятся к решению непрерывной задачи. В случае многомерных схем это максимум из шагов по каждому из направлений.
Доказательство. Производная Фреше левой части схемы (12) может быть записана в виде
Первые слагаемые в обеих производных не зависят от h, остальные – порядка ![]() . Оператор
. Оператор ![]() при
при ![]() невырожден. Следовательно, при достаточно малых h невырождены и производные Фреше и схемы (12) и вспомогательной схемы. Следовательно, эти схемы устойчивы, и их решения сходятся. Монотонизирующий оператор обладает аппроксимаций, поэтому решение
невырожден. Следовательно, при достаточно малых h невырождены и производные Фреше и схемы (12) и вспомогательной схемы. Следовательно, эти схемы устойчивы, и их решения сходятся. Монотонизирующий оператор обладает аппроксимаций, поэтому решение ![]() также сходится к непрерывному решению.
также сходится к непрерывному решению.
Следующее утверждение, доказанное в [6], формулирует достаточное условие того, чтобы свойства монотонности монотонизированной схемы были лучше, чем свойства монотонности схемы (12).
Утверждение 1. Пусть при некотором выполнены следующие условия.
- Неотрицательный функционал
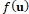 является некоторой мерой немонотонности сеточных функций (чем меньше значение
является некоторой мерой немонотонности сеточных функций (чем меньше значение 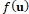 ), тем меньше немонотонность).
), тем меньше немонотонность). - Этот функционал является Липшиц непрерывным в норме
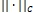 :
:
- Для решения по схеме (12) выполнены соотношения
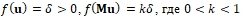 .
. - Для решения по вспомогательной схеме выполнены соотношения
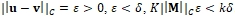 .
.
Тогда ![]() , где
, где
Для выполнения условий утверждения, по существу, нужны два условия: немонотонность решения по схеме (12) и малость ε. При ![]() . Но ε стремится к нулю, как
. Но ε стремится к нулю, как ![]() . Поэтому условия утверждения часто оказываются выполненными. Они могут оказаться невыполненными, например, если схема (12) обладает хорошими свойствами монотонности.
. Поэтому условия утверждения часто оказываются выполненными. Они могут оказаться невыполненными, например, если схема (12) обладает хорошими свойствами монотонности.
Теперь выпишем монотонизированную схему для решения нестационарных задач. Для этого удобнее сначала считать монотонизирующий оператор невырожденным. Тогда из (14) получаем аналогичную запись для нестационарной схемы:
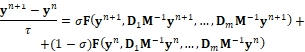 (19)
(19)
Теперь преобразуем эту запись в аналог схемы (13):
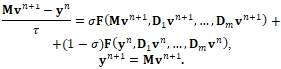 (20)
(20)
Здесь оператор M уже может быть и вырожденным, но тогда при ![]() на первом шаге (при
на первом шаге (при ![]() ) вектор
) вектор ![]() определен неоднозначно. А при
определен неоднозначно. А при ![]() и вектор
и вектор ![]() определен неоднозначно на каждом шаге.
определен неоднозначно на каждом шаге.
Если монотонизирующий оператор любую функцию преобразует в монотонную, то решение по схеме (13) всегда будет монотонным. Из этого следует, что схема (13) не является решением всех проблем немонотонности, так как осцилляции вспомогательной функции v могут сохраняться. Из (14) видно, что вместо осцилляций решения могут существовать осцилляции производных. Но большинство основных физических величин (масса, энергия, импульс) обычно выражаются через функцию, а не через производные. Поэтому монотонизированные схемы позволяют решить довольно много проблем.
- Монотонизирующие операторы.
Если монотонизирующий оператор любую функцию преобразует в монотонную, то он вырожденный. Но можно использовать и невырожденные операторы. Монотонизированные схемы применялись для расчетов движения жидкости в ячейке фильтра [8], для расчетов движения тороидальных вихрей в [9,10], для расчетов переноса начального импульса, а также для расчетов движения расплава в алюминиевом электролизере (все эти задачи с гладкими решениями без ударных волн).
Чтобы не понижать порядок аппроксимации, лучше использовать монотонизирующие операторы с таким же порядком аппроксимации, как у исходной схемы, или выше. Рассмотрим два оператора для схемы (6). Первый оператор вычисляет значения по трем точкам и имеет второй порядок аппроксимации.
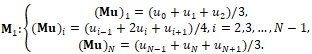 (21)
(21)
У схемы (6) тоже второй порядок точности, но увеличение числа точек для вычисления значений монотонизирующего оператора все равно имеет смысл. Если осцилляции происходят с переменной амплитудой, как на рис. 1, то в трех точках нет информации об изменении этой амплитуды.
Второй оператор вычисляет значения по четырем или пяти точкам:
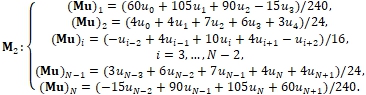 (22)
(22)
В точках от ![]() порядок аппроксимации четвертый, в точках
порядок аппроксимации четвертый, в точках ![]() – второй, в точках
– второй, в точках ![]() – третий. Суммарный порядок аппроксимации второй. Оба оператора являются «линейными неоднородными», т.е. могут быть представлены в виде
– третий. Суммарный порядок аппроксимации второй. Оба оператора являются «линейными неоднородными», т.е. могут быть представлены в виде ![]() – квадратная матрица,
– квадратная матрица, ![]() – вектор-столбец
– вектор-столбец ![]() . Оба оператора невырождены.
. Оба оператора невырождены.
На рис. 2 изображены решения, полученные по схеме (14) с этими операторами, для варианта (б) рис. 1.
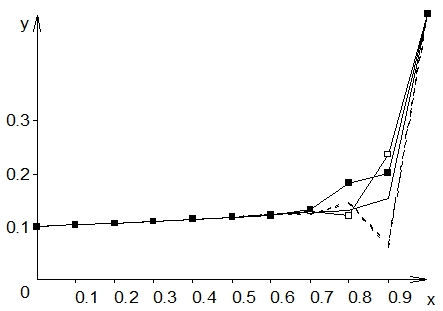
Рис. 2 – Решения по схеме (14). Сплошная линия соединяет значения точного решения в узлах сетки. Пунктирные линии решения по схеме (12) и вспомогательным схемам. Прозрачные маркеры – решение по схеме (14) с оператором M1. Черные маркеры – решение по схеме (14) с оператором M2
Решения u по схеме (12) и v по вспомогательным схемам, как и говорится в утверждении 2, почти не отличаются (сливающиеся пунктирные линии). Решение y с оператором M2 монотонно, а с оператором M1 – нет. В смысле точности, в точке ![]() решение с оператором M1 точнее, а в точке
решение с оператором M1 точнее, а в точке ![]() точнее решение с оператором M2. У обоих решений по монотонизированной схеме видны осцилляции вторых производных.
точнее решение с оператором M2. У обоих решений по монотонизированной схеме видны осцилляции вторых производных.
Если считать, что ![]() отличаются мало, то для исследования монотонности решения
отличаются мало, то для исследования монотонности решения ![]() достаточно исследовать монотонность функции
достаточно исследовать монотонность функции ![]() . Из формул (9) и (21) получаем, что для схемы (6) и оператора M1
. Из формул (9) и (21) получаем, что для схемы (6) и оператора M1
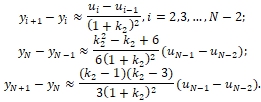 (23)
(23)
Из этих формул следует, что если решение по исходной схеме немонотонно, то и решение по монотонизированной схеме с оператором M1 немонотонно. Но амплитуда колебаний уменьшится (см. рис. 2).
Из формул (9) и (22) получаем, что для схемы (6) и оператора M2
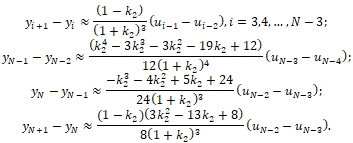 (24)
(24)
Из первой формулы в (24) следует, что если решение по исходной схеме немонотонно, то и решение по монотонизированной схеме с оператором M2, вообще говоря, немонотонно. Но в точках около границы значения оператора вычисляются по другим формулам, поэтому на рис. 2 решение получилось монотонным.
Заметим, что вспомогательная функция v не обязана удовлетворять тем же граничным условиям, что и функции u и y. Например, можно доопределить ![]() . После этого значения
. После этого значения ![]() можно находить по тем же формулам, что и во внутренних точках для оператора M1. А граничные условия для v будут определяться тем, что
можно находить по тем же формулам, что и во внутренних точках для оператора M1. А граничные условия для v будут определяться тем, что ![]() . Монотонизированная разностная схема в этом случае будет такой
. Монотонизированная разностная схема в этом случае будет такой
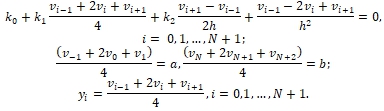 (25)
Из первой формулы (23) следует, что если решение по немонотонизированной схеме (6) немонотонно, то и решение по схеме (25) будет немонотонно (но амплитуда колебаний уменьшится). Кроме того, монотонизирующий оператор в (25) вырожденный, т.к. он отображает
(25)
Из первой формулы (23) следует, что если решение по немонотонизированной схеме (6) немонотонно, то и решение по схеме (25) будет немонотонно (но амплитуда колебаний уменьшится). Кроме того, монотонизирующий оператор в (25) вырожденный, т.к. он отображает Заключение
В статье рассмотрены основные принципы практического применения монотонизированных разностных схем, доказаны некоторые теоретические свойства. Выведено приблизительное достаточное условие монотонности для немонотонизированной схемы. Показано, что в результате монотонизации амплитуда осцилляций может уменьшаться без изменения условия монотонности. Возможно и получение монотонных схем. Рассмотрены примеры монотонизирующих операторов. Все это существенные инструменты для практического решения многих вычислительных задач.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Самарский А.А. Устойчивость разностных схем / А.А. Самарский, А.В. Гулин. – М.: «Наука», 1973, 415 с.
- Godunov S.K. Difference Schemes: An Introduction to the Underlying Theory / S.K. Godunov, V.S. Ryabenkii // Elsevier Science Ltd (1987)
- Трощиев В.Е. Монотонные разностные схемы с весом для уравнения переноса в плоском слое / В.Е. Трощиев , Ю.В. Трощиев // Математическое моделирование, т. 15, № 1, 2003, с. 3-13.
- Трощиев Ю.В. Монотонизация разностных схем внедрением специального оператора // Тихоновские чтения, 14 июня 2011г., М:МАКС Пресс, Тезисы докладов, стр. 73-74.
- Трощиев Ю.В. Монотонизация разностных схем встраиванием монотонизирующих операторов // Москва, МАКС Пресс, 2012, 12 стр.
- Troshchiev Yu. V. Improvement of the monotonicity properties of the difference schemes by building in them of the monotonizing operators // Cornell University, arxiv:1403.3046, USA, 2014, 18 p.
- Рихтмайер Р. Разностные методы решения краевых задач / Р. Рихтмайер, К. Мортон. – М.: Мир, 1972, 418 с.
- Трощиев Ю.В. Исследование процессов внутри пористого фильтра // Труды восьмой Всероссийской научной конференции с международным участием «Математическое моделирование и краевые задачи» 15-17 сентября 2011 г., Часть 2, Секция: Моделирование и оптимизация динамических систем и систем с распределенными параметрами, Самара 2011, с. 104-115.
- Юсупалиев У. Вихревые кольца и плазменные тороидальные вихри в однородных неограниченных средах. II. Исследование процесса образования вихря / У. Юсупалиев, Н.П. Савенкова, Ю.В. Трощиев и др. // Краткие сообщения по физике ФИАН, № 9, 2011 г., с. 46-58.
- Юсупалиев У. Численное моделирование процесса образования тороидальных вихрей / У. Юсупалиев, Р.Н. Кузьмин, Н.П. Савенкова и др. // Сб. тезисов докладов конф. Ломоносовские чтения, Секция физики, 14-23 ноября 2011 г., стр. 209-217.
Список литературы на английском языке / References in English
- Samarskij A.A. Ustojchivost' raznostnyh shem [Numerical Methods] / A.A. Samarskij, A.V. Gulin. – M.: «Nauka», 1973, 415 p. [in Russian]
- Godunov S.K. Difference Schemes: An Introduction to the Underlying Theory / S.K. Godunov, V.S. Ryabenkii // Elsevier Science Ltd (1987)
- Troshhiev V.E. Monotonnye raznostnye shemy s vesom dlja uravnenija perenosa v ploskom sloe [Monotonous Difference Schemes with a Weight for Transport Equation in the Flat Layer] / V.E. Troshhiev , Ju.V. Troshhiev // Matematicheskoe modelirovanie [Math. Modeling] V. 15, 1, P. 3-13. ( 2003) [in Russian]
- Troshhiev Ju.V. Monotonizacija raznostnyh shem vnedreniem special'nogo operatora [Monotonization of Difference Schemes by Building in Them of Special Operator] // Tihonovskie chtenija [Book of Theses of sci. conf. Tikhonov Sess]., (June 2011) P. 73-74. [in Russian]
- Troshhiev Ju.V. Monotonizacija raznostnyh shem vstraivaniem monotonizirujushhih operatorov [Monotonization of Difference Schemes by Integration in Them of Monotonizing Operators]. Maks-Press, Moscow ( 2012) [in Russian]
- Troshchiev Yu. V. Improvement of the monotonicity properties of the difference schemes by building in them of the monotonizing operators. Cornell University, arxiv:1403.3046, USA, 2014, 18 p.
- R.D. Richtmyer, K.W. Morton Difference Methods for Initial-Value Problems. – Interscience Publishers, John Willey & Sons, New York, London, Sydney, 1967.
- Troshhiev Ju.V. Issledovanie processov vnutri poristogo fil'tra [Investigation of Processes in Porous Filter] // Trudy vos'moj Vserossijskoj nauchnoj konferencii s mezhdunarodnym uchastiem «Matematicheskoe modelirovanie i kraevye zadachi» [Proc. of VIII conf. “Mathematical Modeling and Boundary-Value Problems”], Part 2, Samara 104-115 (2011) [in Russian]
- Jusupaliev U. Vihrevye kol'ca i plazmennye toroidal'nye vihri v odnorodnyh neogranichennyh sredah. II. Issledovanie processa obrazovanija vihrja [Vortex rings and plasma toroidal vortices in homogeneous unbounded media. II. The study of vortex formation process] / U. Jusupaliev, N.P. Savenkova, Ju.V. Troshhiev i dr. // Kratkie soobshhenija po fizike FIAN [Bulletin of the Lebedev Physics Institute], V. 38, No. 9, 2011, P. 275-282. DOI: 10.3103/S1068335611090065 [in Russian]
- Jusupaliev U. Chislennoe modelirovanie processa obrazovanija toroidal'nyh vihrej [Numerical modeling of toroidal vortices forming] / U. Jusupaliev, R.N. Kuz'min, N.P. Savenkova i dr. // Sb. tezisov dokladov konf. Lomonosovskie chtenija, Sekcija fiziki [Book of theses of sci. conf. Lomonosov Readings, Section of Physics], November 14-23 (2011), P. 209-217. [in Russian]
