РЕШЕНИЕ ОДНОРОДНОЙ КРАЕВОЙ ЗАДАЧИ РИМАНА С УСЛОВИЕМ НА ДЕЙСТВИТЕЛЬНОЙ ОСИ И БЕСКОНЕЧНЫМ ИНДЕКСОМ ЛОГАРИФМИЧЕСКОГО ПОРЯДКА НОВЫМ МЕТОДОМ
РЕШЕНИЕ ОДНОРОДНОЙ КРАЕВОЙ ЗАДАЧИ РИМАНА С УСЛОВИЕМ НА ДЕЙСТВИТЕЛЬНОЙ ОСИ И БЕСКОНЕЧНЫМ ИНДЕКСОМ ЛОГАРИФМИЧЕСКОГО ПОРЯДКА НОВЫМ МЕТОДОМ
Научная статья
Салимов Р.Б.1, Горская Т.Ю.2, *
1 ORCID: 0000-0003-4177-4830;
2 ORCID: 0000-0001-7136-8388;
1, 2 Казанский государственный архитектурно-строительный университет, Казань, Россия
* Корреспондирующий автор (gorskaya0304[at]mail.ru)
АннотацияРассматривается однородная краевая задача Римана с краевым условием на действительной оси для функции, аналитической в комплексной плоскости кроме точек действительной оси. В краевом условии предельное значение искомой аналитической функции в любой точке действительной оси при подходе сверху представляется как произведение значения заданной функции, называемой коэффициентом, и предельного значения функции в указанной точке при подходе снизу. Предполагается, что модуль коэффициента удовлетворяет условию Гельдера всюду на действительной оси, включая бесконечно удаленную точку, а аргумент коэффициента удовлетворяет условию Гельдера на любой конечной части оси и неограниченно растет как степень логарифма координаты точки оси при неограниченном удалении этой точки от начала координат. Выводится формула, определяющая аналитическую в верхней полуплоскости функцию, мнимая часть которой при стремлении координаты точки оси к положительной бесконечности является бесконечно большой того же порядка, что и аргумент коэффициента краевого условия. Далее строится соответствующая функция в нижней полуплоскости, затем вводятся аналитические функции мнимые части которых обращаются в бесконечность того же порядка, что и аргумент коэффициента краевого условия, когда точки отрицательной действительной оси удаляются в бесконечность. Использование указанных функций позволяет устранить бесконечный разрыв аргумента коэффициента краевого условия аналогично тому, как это делается в случае конечных разрывов этого коэффициента. На основе приемов, аналогичных применяемым Ф.Д. Гаховым, задача приводится к задаче с краевым условием на действительной оси и конечным индексом. Для решения последней задачи используется метод Ф.Д. Гахова. Найденное решение зависит от произвольной целой функции нулевого порядка, модуль которой подчинен дополнительным условиям, в то время как в случае конечного индекса решение задачи зависит от произвольного многочлена степени не выше индекса задачи.
Ключевые слова: краевая задача Римана, аналитическая функция, бесконечный индекс, логарифмический порядок.
SOLUTION OF HOMOGENEOUS RIEMANN BOUNDARY-VALUE PROBLEM WITH A CONDITION ON A REAL AXIS AND AN INFINITE INDEX OF LOGARITHMIC ORDER WITH THE NEW METHOD
Research article
Salimov R.B.1, Gorskaya T.Yu.2, *
1 ORCID: 0000-0003-4177-4830;
2 ORCID: 0000-0001-7136-8388;
1, 2 Kazan State University of Architecture and Civil Engineering, Kazan, Russia
* Corresponding author (gorskaya0304[at]mail.ru)
AbstractWe consider the homogeneous Riemann boundary-value problem with the boundary condition on the real axis for a function analytic in the complex plane except for points of the real axis. In the boundary condition, the limit value of the desired analytic function at any point on the real axis when approaching from above is represented as the product of the value of a given function called the coefficient, and the limit value of the function at the specified point at the bottom approaching. We assume that the coefficient modulus satisfies the Hölder condition everywhere on the real axis, including the infinitely distant point, and the coefficient argument satisfies the Hölder condition on any finite part of the axis and increases indefinitely as the degree of logarithm coordinates of the axis point with unlimited distance from the origin. The authors derived the formula that determines an analytic function in the upper half-plane the imaginary part of which as the coordinate of the axis point tends to positive infinity is infinitely large of the same order as the argument of the coefficient of the boundary condition. Next, the corresponding function is constructed in the lower half-plane, then analytical functions are introduced the imaginary parts of which turn into the infinity of the same order as the argument of the coefficient of the boundary condition when the points of the negative real axis are removed to infinity. The use of these functions allows us to eliminate the infinite gap of the argument of the coefficient of the boundary condition in the same way as it is done in the case of finite discontinuities of this coefficient. Based on techniques similar to those used by F.D. Gakhov, the problem is reduced to a problem with a boundary condition on the real axis and a finite index. Gakhov’s method is used to solve the last problem. The solution found depends on an arbitrary entire function of order zero, the modulus of which is subject to additional conditions, while in the case of a finite index the solution of the problem depends on an arbitrary polynomial of degree not higher than the index of the problem.
Keywords: Riemann's boundary value problem, analytic function, infinite index, logarithmic order.
Введение Постановка задачиПусть D+, D- - соответственно верхняя и нижняя полуплоскости в плоскости комплексного переменного z = x + iy с действительной осью L, Φ+(z), Φ-(z) - функции, аналитические соответственно в области D+, D-. Задачей Римана называется следующая задача [1, с. 106]: требуется определить функции Φ+(z), Φ-(z), ограниченные аналитические в областях D+, D- соответственно, если их граничные значения удовлетворяют условию
![]() (1)
(1)
в котором коэффициент G(t), g(t) - заданные на L функции.
В случае, когда lnG(t) и g(t) - функции, удовлетворяющие условию Гельдера (условию H) всюду на L, включая окрестность точки t = ∞ [2, с. 67] решение задачи (1) дано монографиях [1, с. 118 - 121], [2, с. 136 – 139].
Решение задачи зависит от ее индекса равного (arg G(+∞) - arg G(-∞)) /2π.
Начало исследования задачи (1) в случае, когда ее индекс обращается в бесконечность степенного порядка, было положено Н.В. Говоровым. Результаты его работ в дальнейшем вошли в монографию [3].
Краткие сведения о развитии этого научного направления проведены в статье [4]. Дополняя эти сведения, отметим, что задача Римана с бесконечным индексом логарифмического порядка рассмотрены в работах [5], [6], [7].
Авторы указанного ряда работ решение задачи Римана получают путем построения канонического решения – частного решения однородной задачи
![]() (2)
(2)
обладающего нужными свойствами, аналогично тому, как было сделано ранее Н.В. Говоровым.
В статье [8] для решения однородной задачи Римана с бесконечным индексом логарифмического порядка и краевым условием (2), заданным на положительной действительной оси, используется другой метод, основанный на устранении бесконечного разрыва arg G(t) и аналогичный тому, с помощью которого в работе [1, C. 428 – 439] устранялись разрывы первого рода у функций ln G(t).
В настоящей работе на основе результатов статьи [8] находится решение однородной задачи с бесконечным индексом логарифмического порядка и краевым условием (2), заданным на всей действительной оси.
Требуется определить функции Φ+(z) и Φ-(z), ограниченные аналитические в областях D+, D- соответственно, если их граничные значения удовлетворяют условию (2), а для коэффициента G(t) выполняются следующие предположения: ln|G(t)| удовлетворяет условию H всюду на L, включая бесконечно удаленную точку (ln |G(t)| ∈ H, t ∈ L),
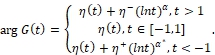 (3)
(3)
![]() - действительные числа, α > 0, α* >0, lntα >0 при
- действительные числа, α > 0, α* >0, lntα >0 при ![]() поэтому, в частности,
поэтому, в частности, ![]() . Для простоты примем, что
. Для простоты примем, что ![]()
Если последнее соотношение для заданной функции ![]() не выполняется, то с помощью приемов, аналогичных использованным в книге [1, C. 428–439] рассматриваемую задачу можно привести к задаче для новой искомой функции, в которой указанное соотношение имеет место.
не выполняется, то с помощью приемов, аналогичных использованным в книге [1, C. 428–439] рассматриваемую задачу можно привести к задаче для новой искомой функции, в которой указанное соотношение имеет место.
Вспомогательные соотношения
Пусть α > 0 - действительное положительное число. Для ln z = ln |z|+i arg z, 0 arg z под (ln z -iπ)α будем понимать непрерывную однозначную аналитическую в полуплоскости Im z > 0 функцию, которая при z = |x|eiπ, |x| > 1 принимает положительное значение (ln |x|)α, (arg (ln |x|)α = 0), и arg (ln z –iπ)α → 0 при z = x → +∞.
Пользуясь обозначением
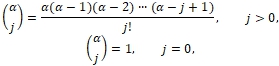
считая, что ![]()
При ![]() второй множитель правой части последней формулы представим как сумму степенного ряда с учетом разложения, полученного из (4) заменой α на α+1 и придем к соотношению
второй множитель правой части последней формулы представим как сумму степенного ряда с учетом разложения, полученного из (4) заменой α на α+1 и придем к соотношению
![]() (6)
(6)
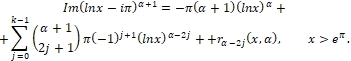 (8)
где
(8)
где
В формуле (8) число α заменим на α - 2m, число k на k-m, когда m принимает последовательно значения 1, 2, ..., k-1 и придем к соотношению
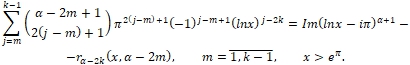 (10)
(10)
Где
![]() (11)
(11)
Ясно, что здесь целесообразно считать, что ![]()
Соотношения (10) представляют собой систему равенств, содержащих величины ![]() . Коэффициенты при этих величинах образуют треугольную матрицу
. Коэффициенты при этих величинах образуют треугольную матрицу ![]() элементы которой
элементы которой ![]() Определитель этой матрицы равен
Определитель этой матрицы равен
![]()
причем ![]() т.к. согласно (7) имеем -3 < α - 2k и 0 < α - 2(k-1)+1. Пусть Amj - алгебраическое дополнение для элемента amj определителя Δ.
т.к. согласно (7) имеем -3 < α - 2k и 0 < α - 2(k-1)+1. Пусть Amj - алгебраическое дополнение для элемента amj определителя Δ.
Из системы (10) по формулам Крамера выразим ![]() , через правые части соотношений системы
, через правые части соотношений системы
![]()
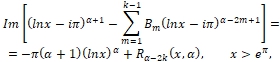 (12)
Где
(12)
Где
![]() (13)
(13)
каждое слагаемое которой есть однозначная ветвь в полуплоскости Im z>0, определяемая как указано выше. Мнимая часть этой функции при z=|x|eiπ , |x|>1, обращается в нуль, а при z=x, x > eiπ, имеет представление, определенное формулой (12), в которой ![]() при x →+∞ в силу (13), (11), (7).
при x →+∞ в силу (13), (11), (7).
Функция T0(z) является вспомогательной в связи с тем, что она имеет особенность в точке z=0. По этой причине введем в рассмотрение аналитическую, однозначную и непрерывную во всех конечных точках полуплоскости ![]() функцию
функцию
![]() (15)
(15)
считая, что T(z)=T0 (z+i), Im z≥0.
Для Im T(x) при x > eiπ можно получить представление, аналогичное (12). Но проще воспользоваться представлением (12) и учесть, что Im (T(x)-T0(x)) →0 при x →+∞.
Обозначим
![]() (16)
(16)
Подставляя сюда выражения для T0(z) и T(z), учитывая формулы (14), (5), при z=x, x > eiπ путем непосредственного подсчета убедимся в том, что имеют место соотношения
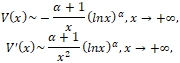 (17)
(17)
а при x → - ∞ выполняются соотношения, получаемые из предыдущих формул (17) заменой ln x на ln |x|.
Используя вышесказанное поведение производной V’(x) при x → +∞, принимая во внимание результат книги
[3, C. 127], заключаем, что V(x) - функция, удовлетворяющая условию Гельдера в окрестности точки x → +∞ (дифференцируемая в любой конечной точке x > eiπ). Сказанное справедливо и для окрестности точки x → - ∞.
Формулу (13) с учетом (9), (11) запишем так
![]() (18)
(18)
Где
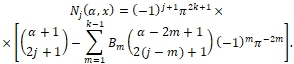 (19)
(19)
При ![]() согласно (7) мы должны взять k=1 и в предыдущих формулах будут отсутствовать конечные суммы, в которых
согласно (7) мы должны взять k=1 и в предыдущих формулах будут отсутствовать конечные суммы, в которых ![]() при k=1 дополнительно будем иметь
при k=1 дополнительно будем иметь ![]() причем последние два равенства выполняются и в случае α=2k-1>1.
причем последние два равенства выполняются и в случае α=2k-1>1.
В дальнейшем будем считать, что α=2k-1<-1, помня, что в полученных формулах при α=2k-1 надо положить ![]()
В силу (18), (19) имеем
![]()
Таким образом, в случае α>0 приходим к следующей лемме.
Лемма. При вышеуказанных условиях для значений мнимой части аналитической в полуплоскости Im z ≤0 функции T(z) формулы (15) при z=x, |x|> eiπ справедливы представления (21), (22) в которых V(x) - функция, удовлетворяющая условию Гельдера и обращающаяся в нуль на бесконечности, ![]() выражается формулой (20) и исчезает при натуральном числе α.
выражается формулой (20) и исчезает при натуральном числе α.
Зная функцию T(z) формулы (15), найдем аналитическую в полуплоскости Im z<0 функцию, определяемую формулой [2,с. 140, 141].
![]() (23)
(23)
Пусть α* - действительное положительное число. Под ![]() , когда ln z = ln|z|+iargz,
, когда ln z = ln|z|+iargz, ![]() , будем понимать непрерывную однозначную в полуплоскости Im z<0 функцию, которая при z=x>1 принимает положительное значение
, будем понимать непрерывную однозначную в полуплоскости Im z<0 функцию, которая при z=x>1 принимает положительное значение ![]() .
.
Здесь при ![]() согласно формуле (6) имеем
согласно формуле (6) имеем
![]()
(когда ![]() ).
).
Отсюда ясно, что в полученных на основании (6) формулах, включая (13), величины α, k, x в случае ![]() можно заменить соответственно на
можно заменить соответственно на ![]() .
.
При этом определитель системы, получаемой из (10), с элементами ![]() , будет равен
, будет равен
причем
![]()
По значениям ![]() - алгебраического дополнения для
- алгебраического дополнения для ![]() вычисляется
вычисляется
![]()
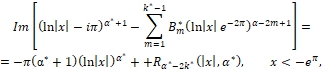 (26)
Где
(26)
Где
каждое слагаемое которой является однозначной непрерывной ветвью в полуплоскости Imz<0, определяемой как указано выше.
Заменяя в формуле (28) z на z-i получим функцию
![]() (29)
(29)
непрерывную аналитическую в полуплоскости Im ![]() с единственной особой точкой z = ∞.
с единственной особой точкой z = ∞.
Введем в рассмотрение функцию
![]() (30)
(30)
значения которой на действительной оси в окрестности точки x = ∞ обладают теми же свойствами, что и V(x) (при ![]() ).
).
На основании формул (18) –(20) получаем
![]()
Где
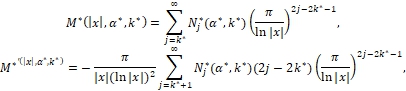
![]() определяется формулой, получаемой из (19) заменой
определяется формулой, получаемой из (19) заменой ![]() соответственно на
соответственно на ![]() . При
. При ![]() в силу (25) здесь и с формуле (26), (27) будут отсутствовать конечные суммы, в которых
в силу (25) здесь и с формуле (26), (27) будут отсутствовать конечные суммы, в которых ![]() при
при ![]() дополнительно будем иметь
дополнительно будем иметь ![]() причем последние два равенства выполняются и в случае
причем последние два равенства выполняются и в случае ![]()
В дальнейшем будем считать, что ![]() учитывая, что при
учитывая, что при ![]() формулы упростятся.
формулы упростятся.
При z = x, x >1 согласно (28) имеем ![]() поэтому с учетом (30) получаем
поэтому с учетом (30) получаем
![]() (31)
(31)
Таким образом, мы получили соотношения (31), (32), аналогичные приведенным в вышеуказанной лемме.
Как и выше, имея функцию ![]() формулы (29), определим аналитическую в полуплоскости
формулы (29), определим аналитическую в полуплоскости ![]() функцию
функцию
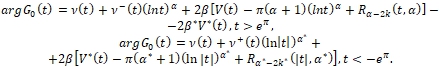 В дальнейшем будем считать, что числа
В дальнейшем будем считать, что числа причем ![]() функция, удовлетворяющая условию H на любой конечной части L.
функция, удовлетворяющая условию H на любой конечной части L.
Согласно (3) ![]() поэтому
поэтому ![]() удовлетворяет условию H всюду на L, включая t = ∞.
удовлетворяет условию H всюду на L, включая t = ∞.
Далее находим аналитическую в полуплоскостях Im z > 0 и Im z < 0 функцию [1, C. 110]
![]() (40)
(40)
значения которой на L как слева, так и справа удовлетворяют условию H на любой конечной части L [2, С. 66, 68], поэтому интеграл этой формулы
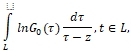 (41)
(41)
является функцией, непрерывной в любой конечной точке ![]() . Принимая во внимание представления (38), (39), представления (17) для V(x), V’(x), а также аналогичные для V*, V*’, на основании результатов статьи [10], примененные для случая, когда имеют место вышеуказанные представления для плотности
. Принимая во внимание представления (38), (39), представления (17) для V(x), V’(x), а также аналогичные для V*, V*’, на основании результатов статьи [10], примененные для случая, когда имеют место вышеуказанные представления для плотности ![]() интеграла (41), придем к заключению, что существует конечный предел этого интеграла как при t → +∞, так и при t → -∞.
интеграла (41), придем к заключению, что существует конечный предел этого интеграла как при t → +∞, так и при t → -∞.
Следовательно, интеграл (41) является ограниченной функцией на L. Поэтому функции ![]() формулы (40) являются аналитическими ограниченными функциями соответственно в полуплоскостях D+ и D-.
формулы (40) являются аналитическими ограниченными функциями соответственно в полуплоскостях D+ и D-.
Зная последние функции, определим ограниченные аналитические в областях D+ и D- соответственно функции
![]()
![]()
отличные от нуля всюду в указанных областях, включая границу L, являющиеся значениями функции ![]() .
.
Найденные функции удовлетворяют краевому условию
![]() (42)
(42)
![]() (43)
(43)
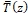 формул (29), (33) обозначим соответственно
формул (29), (33) обозначим соответственно
где ![]() при Im z > 0,
при Im z > 0, ![]() при Im z < 0, является целой функцией, так как левая и правая части условия (45) есть граничные значения функций, аналитических в полуплоскостях соответственно D+ и D- и эти значения равны в любой точке t действительной оси.
при Im z < 0, является целой функцией, так как левая и правая части условия (45) есть граничные значения функций, аналитических в полуплоскостях соответственно D+ и D- и эти значения равны в любой точке t действительной оси.
Из (46) находим функцию
![]() (47)
(47)
которая удовлетворяет краевому условию (2), т.е. является решением этой краевой задачи (2) и содержит произвольную целую функцию F(z).
Пусть ![]() ограниченное решение краевой задачи (2). Замечая, что 1/X(z) есть ограниченная функция, заключаем, что
ограниченное решение краевой задачи (2). Замечая, что 1/X(z) есть ограниченная функция, заключаем, что
![]() (48)
(48)
Где ![]() . Принимая во внимание формулу (46) для целой функции F(z) и учитывая формулы (15), (23), (29), (33), (43), (44), приходим к выводу, что порядок целой функции F(z), равен нулю [11, с. 245].
. Принимая во внимание формулу (46) для целой функции F(z) и учитывая формулы (15), (23), (29), (33), (43), (44), приходим к выводу, что порядок целой функции F(z), равен нулю [11, с. 245].
При этом в силу (46), (48) будем иметь
![]()
Таким образом, мы пришли к следующей теореме.
Теорема 1. Если краевая задача (2) имеет ограниченное решение ![]() , то оно определяется формулой (47), в которой F(z) - целая функция нулевого порядка, удовлетворяющая условию (49).
, то оно определяется формулой (47), в которой F(z) - целая функция нулевого порядка, удовлетворяющая условию (49).
Справедлива и обратная теорема
Теорема 2. Если F(z) - любая целая функция нулевого порядка, удовлетворяющая условию (49), то ограниченное решение краевой задачи (2) определяется формулой (47).
В самом деле, используя указанную в этой теореме функцию F(z), мы по формуле (47) найдем функцию ![]() , удовлетворяющие краевому условию (2). Остается установить ограниченность этих функций. Учитывая, что F(z) - функция нулевого порядка, и выражения для
, удовлетворяющие краевому условию (2). Остается установить ограниченность этих функций. Учитывая, что F(z) - функция нулевого порядка, и выражения для ![]() придем к заключению, что порядок функции
придем к заключению, что порядок функции ![]() формулы (47) в каждой из полуплоскостей Im z>0 и Im z<0 равен нулю [12, с. 69].
формулы (47) в каждой из полуплоскостей Im z>0 и Im z<0 равен нулю [12, с. 69].
Но в силу условия (49) и формулы (47) будет выполняться неравенство ![]() . Поэтому согласно теореме Фрагмена-Линделера [2, C. 69], [11, C. 206, 211] всюду в области
. Поэтому согласно теореме Фрагмена-Линделера [2, C. 69], [11, C. 206, 211] всюду в области ![]() будем иметь
будем иметь ![]() что требовалось установить.
что требовалось установить.
Показатель правой части формулы (49) с учетом (37) можно записать так
![]() (50)
(50)
t → -∞ или t → +∞, то целая функция нулевого порядка F(z), удовлетворяющая неравенству (49), обращается в нуль тождественно: F(z) ≡ 0 [11, C. 256]. В этом случае по формуле (47) мы получаем только нулевое решение краевой задачи (2)}.
Из формул (50), (51) в частности, видно, что при выполнении любого из следующих условий
![]() (53)
(53)
будет иметь место соотношение (52) и краевая задача (2) будет иметь только нулевое решение.
Итак, справедлива
Теорема 3. Если выполняется условие \(52), в частности, имеет место любое из трех условий (53), то краевая задача (2) имеет только нулевое решение.
Заключение
Таким образом, дано новое прозрачное решение задачи Римана с краевым условием на действительной оси, когда индекс задачи обращается в бесконечность логарифмического порядка, когда ![]() при
при ![]() с различными вообще говоря, показателями α и α*. Это решение в общем случае содержит произвольную целую функцию нулевого порядка, удовлетворяющую действительному условию (49), т.е. задача имеет бесконечное множество решений.
с различными вообще говоря, показателями α и α*. Это решение в общем случае содержит произвольную целую функцию нулевого порядка, удовлетворяющую действительному условию (49), т.е. задача имеет бесконечное множество решений.
В отдельных случаях рассматриваемая задача имеет только нулевое решение.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Гахов Ф.Д. Краевые задачи / Ф.Д. Гахов. – М.: Наука, 1977. – 641 с.
- Мусхелишвили Н.И. Сингулярные интегральные уравнения / Н.И. Мусхелишвили. – М.: Наука, 1968. – 511 с.
- Говоров Н.В. Краевая задача Римана с бесконечным индексом / Н.В. Говоров. – М.: Наука, 1986. – 239 с.
- Салимов Р.Б. Новый подход к решению однородной краевой задачи Римана на луче с бесконечным индексом / Р.Б. Салимов, А.З. Сулейманов// Известия вузов. Математика. №5, 2017, С. 71 – 76.
- Юров П.Г. Однородная краевая задачи Римана с бесконечным индексом логарифмического типа / Юров П.Г. // Изв. вузов. Матем. 1966, № 2, С. 158–163.
- Алекна П.Ю. Неоднородная краевая задача Римана с бесконечным индексом логарифмического порядка 0 <γ <1 для полуплоскости / П.Ю. Алекна // Литовский математический сборник. 1974, т. XIV, № 3, С. 5-18.
- Алекна П.Ю. Краевая задача Гильберта с бесконечным индексом логарифмического порядка для полуплоскости / П.Ю. Алекна // Литовский математический сборник. 1977, т. XVII, № 1, С. 5-12.
- Салимов Р.Б. Решение однородной краевой задачи Римана с бесконечным индексом логарифмического порядка на луче новым методом / Р.Б. Салимов, Э.Н. Хасанова // Изв. Сарат. ун-та. Нов. Сер. Математика. Механика. Информатика. 2017. Т. 17, вып. 2. С. 160-171.
- Маркушевич А.И. Теория аналитических функций / А.И. Маркушевич. Т. 1. – М.: Наука, 1967. – 486 с.
- Salimov R. B. The behavior of a singular integral with the Hilbert kernel near a point where the density of the integral is weakly continuous / R. B. Salimov // Rassian Mathematics. 2012,V. 56,I.6, pp. 52–56.
- Маркушевич А.И. Теория аналитических функций / А.И. Маркушевич. Т. 2. – М.: Наука, 1968. – 624 с.
- Левин Б.Я. Распределение корней целых функций/ Б.Я. Левин. –М.: Гостехиздат, 1956. – 632 с.
Список литературы на английском языке / References in English
- Gahov F.D. Kraevye zadachi [Boundary value problems] / Gahov F.D. M.: Nauka, 1977. – 641 s. [in Russian]
- Mushelishvili N.I. Singuljarnye integral'nye uravnenija [Singular integral equations] / Mushelishvili N.I. M.: Nauka, 1968. – 511 s. [in Russian]
- Govorov N.V. Kraevaja zadacha Rimana s beskonechnym indeksom [The Riemann boundary value problem with infinite index] / Govorov N.V. M.: Nauka, 1986. – 239 s. [in Russian]
- Salimov R.B. Novyj podhod k resheniju odnorodnoj kraevoj zadachi Rimana na luche s beskonechnym indeksom [A new approach to the solution of a homogeneous boundary value problem of Riemann on the beam with infinite index ] / Salimov R.B., Sulejmanov A.Z. // Izvestija vuzov. Matematika. [Izvestiya vuzov. Math] [№5, 2017, S. 71 – 76. [in Russian]
- Yurov P. G. Odnorodnaya krayevaya zadacha Rimana s beskonechnym indeksom logarifmicheskogo tipa [A homogeneous Riemann boundary Value problem with an infinite index of logarithmic type]/ Yurov P. G. // Izv. vyssheye obrazovaniye. Mod. 1966, № 2, s. 158-163 [in Russian]
- Alekna P.Yu. Neodnorodnaya krayevaya zadacha Rimana s beskonechnym indeksom logarifmicheskogo poryadka 0 <g <1 dlya poluploskosti [Inhomogeneous Riemann boundary value problem with an infinite index of logarithmic order 0 <γ <1 for a half-plane] / P.Yu. Alekna // Litovskiy matematicheskiy sbornik. 1974, t. XIV, № 3, S. 5-18. [in Russian]
- Alekna P.Yu. Krayevaya zadacha Gil'berta s beskonechnym indeksom logarifmicheskogo poryadka dlya poluploskosti [Hilbert's boundary value problem with an infinite index of logarithmic order for a half-plane]/ P.Yu. Alekna // Litovskiy matematicheskiy sbornik. 1977, t. XVII, № 1, S. 5-12. [in Russian]
- Salimov R.B. Resheniye odnorodnoy krayevoy zadachi Rimana s beskonechnym indeksom logarifmicheskogo poryadka na luche novym metodom [Solution of the homogeneous Riemann boundary value problem with an infinite index of logarithmic order on the ray by a new method] / R.B. Salimov, E.N. Khasanova // Izv. Sarat. un-ta. Nov. Ser. Matematika. Mekhanika. Informatika. 2017. T. 17, vyp. 2. S. 160-171. . [in Russian]
- Markushevich A.I. Teorija analiticheskih funkcij. [The theory of analytic functions ] / Markushevich A.I. Vol. 1. M.: Nauka, 1967. – 486 s. [in Russian]
- Salimov R. B. The behavior of a singular integral with the Hilbert kernel near a point where the density of the integral is weakly continuous / R. B. Salimov // Rassian Mathematics. 2012,V. 56,I.6, pp. 52–56.
- Markushevich A.I. Teorija analiticheskih funkcij. [The theory of analytic functions ] / Markushevich A.I. Vol. 2. M.: Nauka, 1968. – 624 s. [in Russian]
- Levin B.Ja. Raspredelenie kornej celyh funkcij. [The distribution of roots of entire functions] / Levin B.Ja. M.: Gostehizdat, 1956. – 632 s. [in Russian]
