О ВЛИЯНИИ ПРОДОЛЬНОГО ДВИЖЕНИЯ ПЫЛИ НА УСТОЙЧИВОСТЬ ОДНОРОДНОГО СОСТОЯНИЯ МАГНИТОАТИВНОЙ ПЫЛЕВОЙ ПЛАЗМЫ

О ВЛИЯНИИ ПРОДОЛЬНОГО ДВИЖЕНИЯ ПЫЛИ НА УСТОЙЧИВОСТЬ ОДНОРОДНОГО СОСТОЯНИЯ МАГНИТОАТИВНОЙ ПЫЛЕВОЙ ПЛАЗМЫ

Научная статья

Захаров В.Ю.^1, *, Чернова Т.Г.²

¹ ORCID: 0000-0002-4745-1218;

² ORCID: 0000-0003-0608-0075;

^{1, 2} Калужский филиал Московского государственного технического университет им. Н.Э. Баумана, Калуга, Россия

* Корреспондирующий автор (vladiyuz[at]mail.ru)

Аннотация

Рассматривается распространение низкочастотных электромагнитных волн малой амплитуды в пылевой плазме малого давления. Пыль считается холодной и имеющей как поперечную, так и продольную скорость движения по отношению к направлению внешнего магнитного поля. Аналитически изучается дисперсионное уравнение четвертой степени для фазовых скоростей волн. Получены ограничения на невозмущенные параметры плазмы, при выполнении которых однородное состояние плазмы является устойчивым. Показано, что при отсутствии или достаточно больших значениях составляющей скорости пылевой компоненты вдоль магнитного поля однородное состояние плазмы является неустойчивым относительно малых возмущений.

Ключевые слова: пылевая плазма, волны малой амплитуды, дисперсионное уравнение, устойчивость  однородного состояния  плазмы.

ON EFFECT OF LONGITUDINAL DUST MOTION ON STABILITY OF HOMOGENEOUS STATE OF MAGNETIC DUST PLASMA

Research article

Zakharov V.Yu.^1, *, Chernova Т.G.²

¹ ORCID: 0000-0002-4745-1218;

² ORCID: 0000-0003-0608-0075,

^{1, 2} Kaluga branch of Moscow State Technical University named after N.E. Bauman, Kaluga, Russia* Corresponding author (vladiyuz[at]mail.ru)

Abstract

The propagation of low-frequency electromagnetic waves of small amplitude in a low-pressure dust plasma is considered in the paper. Dust is considered to be cold and has both a transverse and longitudinal velocity relative to the direction of the external magnetic field. The fourth-degree dispersion equation for the phase velocities of waves is analytically studied. Limits on the unperturbed plasma parameters with stable homogeneous state of plasma are obtained. It is shown that in the absence of sufficiently large values of the velocity component of the dust component along the magnetic field, the homogeneous state of plasma is unstable concerning small perturbations.

Keywords: dust plasma, small amplitude waves, dispersion equation, the stability of a homogeneous plasma state.

Проблема электромагнитных волн в пылевой плазме достаточно активно исследуется в последнее время. Присутствие в плазме пылевых частиц и характер их движения оказывают значительное влияние на спектры колебаний в области низких частот. В [7] показано, что даже небольшая концентрация пылевых частиц может приводить к существенной модификации плазменных волн, если пылевая составляющая обладает значительной скоростью вращения вокруг линий магнитного поля. Такие условия реализуются, например, в космической плазме за фронтами ударных волн от сверхновых. При этом пылевые частицы после пересечения фронта волны, распространяющейся перпендикулярно внешнему магнитному полю, начинают вращаться со скоростью порядка трех четвертых от скорости фронта.

В [7] был рассмотрен случай, когда пылевые частицы имеют только поперечную составляющую скорости по отношению к направлению магнитного поля и не перемещаются вдоль линий поля. Было показано, что учет движущейся пыли приводит к повышению порядка дисперсионного уравнения, причем ветвь колебаний, возникающая при наличии вращающейся пыли, всегда является неустойчивой. Данная неустойчивость является апериодической, способ ее возникновения подобен механизму зеркальной неустойчивости и характеризуется захватом пыли в образующиеся ямы магнитного поля.

В [8] изучалось обобщение [7] на случай распространения низкочастотных электромагнитных волн в холодной пылевой плазме. Предполагалось, что пылевая компонента имеет поперечную и продольную скорость движения по отношению к направлению внешнего магнитного поля. В рамках кинетической теории было получено дисперсионное уравнение шестой степени

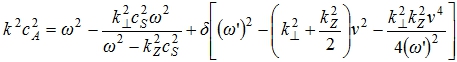   (1)

Здесь ω, k- частота и длина линейной волны, B₀ - внешнее магнитное поле направлено вдоль оси Z,  - составляющие волнового вектора поперек и вдоль магнитного поля соответственно,  - альфвеновская скорость,  - скорость звука,  - отношение плотностей пылевой и ионной компонент, , u и V - составляющие скорости пылевой компоненты вдоль и поперек магнитного поля соответственно.

В [8] рассмотрен частный случай плазмы малого давления . При этом в уравнении (1) можно пренебречь вкладом второго слагаемого в правой части, тогда уравнение (1) примет вид

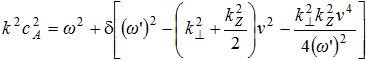   (2)

Уравнение (2) было сведено к уравнению четвертой степени и на основе численного анализа было показано, что наличие продольной составляющей скорости u пылевой компоненты в некотором конечном интервале между малыми и большими значениями приводит к устойчивости.

В настоящей статье проводится аналитическое исследование дисперсионного уравнения (2) с точки зрения получения необходимых и достаточных условий устойчивости, т.е. наличия четырех действительных корней в общем случае. Предложенный ниже геометрический метод позволяет также определить, какие из корней становятся комплексными в случае возникновения неустойчивости.

Для этого введем новые переменные (θ - угол между магнитным полем и волновым вектором)

;

и перепишем (2) в виде

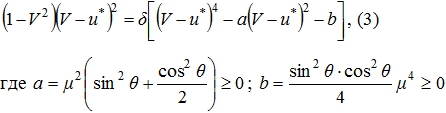
При отсутствии продольной скорости у пылевой компоненты (u*=0) уравнение (3) становится биквадратным и при наличии пыли имеет только два действительных корня.

Пусть  (для определенности u*>0). Сделаем линейную замену t=V-u*; V=t+u*. Уравнение (3) примет вид 

   (4)

Если ввести функцию , то уравнение (4) можно переписать в виде    (5)

Очевидно, что уравнение (3) будет иметь четыре действительных корня, если график функции y=h(t) пересекается с прямой y=δb в верхней полуплоскости четыре раза. Поэтому необходимым условием устойчивости является наличие у функции y=h(t) трех точек экстремума. Производная функции h(t) имеет вид

.

Очевидно, что при y=0  у функции h(t) будет только одна точка экстремума. Поэтому условие

   (6)

является первым необходимым условием устойчивости. Функция h(t) будет иметь три точки экстремума, если, помимо (6), дискриминант квадратного трехчлена в квадратной скобке h'(t) больше нуля

   (7)

Как указано выше, условие (7) является вторым необходимым условием устойчивости. При нарушении (7) уравнение (3) будет иметь менее четырех действительных корней. Приравняв к нулю производную h'(t) при выполнении неравенств (6), (7)  получим три точки экстремума

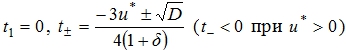
В дальнейшем будем считать неравенства (6), (7) выполненными. В зависимости от знака знак  может быть как положительным, так и отрицательным. Рассмотрим два возможных случая взаимного расположения точек экстремума  и .

1) . В этом случае расположение точек экстремума будет следующим: .

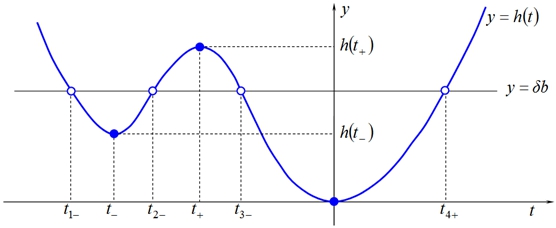
Рис. 1 – Схематичный график функции y=h(t) совместно с графиком горизонтальной прямой y=δb в случае устойчивости

 

Из рис.1 ясно, что эти графики всегда будут иметь четыре общие точки, если будут выполнены следующие неравенства

   (8)

Точки пересечения графиков соответствуют трем отрицательным  и одному положительному  корням дисперсионного уравнения (4).

Вычисления  после несложных преобразований приводят к следующим выражениям

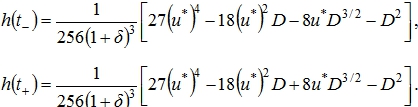   (9)

С учетом (9) неравенства (8) можно свести к виду    (10)

С учетом неравенства (7) получим  необходимое и достаточное условие устойчивости корней уравнения (4) для случая 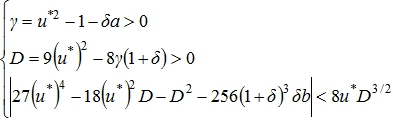1)

   (11)

При малых значениях u* возможно нарушение первого или второго неравенства (11), при достаточно больших значениях u* будет нарушаться третье неравенство (11). Данный вывод полностью согласуется с результатами численного анализа уравнения (3) [8]. Более того, из первых двух неравенств получается нижняя граница значений u* для области устойчивости. Из рис.1 также следует, что при положительных значениях u* уравнение (4) имеет один положительный и три отрицательных корня. Это соответствует тому, что три меньшие фазовые скорости дисперсионного уравнения (2) меньше продольной скорости u пылевой компоненты, большая фазовая скорость всегда превышает .

При нарушении неравенства (8) возможны следующие ситуации:

1) ; в этом случае из рис.1 следует, что графики функций  будут иметь только две точки пересечения , а меньшие отрицательные корни  становятся комплексными.

2) ; в этом случае из рис.1 следует, что графики функций будут иметь только две точки пересечения , а отрицательные корни становятся комплексными.

Для случая u*<0 неравенства (11) модифицируются заменой u* на  в правой части последнего неравенства. При этом график функции y=h(t) зеркально отражается относительно оси у, и, в случае устойчивости, уравнение (4) будет иметь один отрицательный и три положительных корня.

2) . В этом случае расположение точек экстремума будет следующим: .

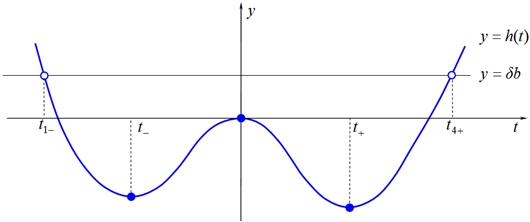
Рис. 2 – Схематичный график функции y=h(t) совместно с графиком горизонтальной прямой y=δb

 

Из рис. 2 ясно, что эти графики всегда будут иметь только две общие точки . Из трех отрицательных корней меньшие по модулю  становятся комплексными, и соответствующие им моды становятся неустойчивыми.

Таким образом, в данной работе получены необходимые и достаточные условия (11) на невозмущенные параметры пылевой плазмы, при выполнении которых дисперсионное уравнение (2) всегда имеет четыре действительных корня. При отсутствии или достаточно больших значениях составляющей скорости пылевой компоненты вдоль магнитного поля однородное состояние плазмы является неустойчивым относительно малых возмущений. Диапазон значений продольной скорости в случае устойчивости однородного состояния определяется неравенствами (11). Также из рис.1 можно получить диапазоны, в которых находятся корни дисперсионного уравнения (2).

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Kuvshinov B.N. Magnetohydrodynamic model for plasma instabilities in the ion-kinetic regime / B.N. Kuvshinov // Plasma Phys. Control. Fusion. - 1994. - V.l. - № 9. - P. 2882-2889.
2. Fortov V. E. Mechanism of dust-acoustic instability in a direct current glow discharge plasma / V. E. Fortov, A. G. Khrapak, S. A. Khrapak and others // Physics of Plasmas. - 2000. - V.7. - № 5. - P. 1374-1380.
3. Фортов В.Е. Физика неидеальной плазмы / В.Е. Фортов, А.Г. Храпак, И.Т. Якубов. - М.: Физматлит, 2004. - 528 с.
4. Shukla P.K. Low-frequency electromagnetic waves in a Hall-magnetohydrodynamic plasma with charged dust macroparticles / P.K. Shukla, I. Kourakis, L. Stenflo // Phys.Plasmas. - 2005. - V.12. - P. 024501-1-4.
5. Shukla P.K. New Generalized Dispersion Relation for Low-Frequency Electromagnetic Waves in a Hall-Magnetohydrodynamic Dusty Plasmas / P.K. Shukla, I. Kourakis, L. Stenflo // New vistas in dusty plasmas. Fourth International Conference on the Physics of Dusty Plasmas. Orleans. France. 13-17 June.2005 / Springer, 2005. - V. 799. - P. 311-314.
6. Prudskikh V.V. Acceleration of dust particles by low-frequency Alfven waves / V.V. Prudskikh, Yu.A. Shchekinov // Physics Letters A. - 2008. - V. 372. - P. 2671-2675.
7. Prudskikh V.V. Mirror instability in a plasma with cold gyrating dust particles / V.V. Prudskikh, L.V. Kostyukova, Yu.A. Shchekinov // Phys. - 2010. - V. 17. - P.033701.
8. Прудских В.В. Низкочастотные электромагнитные неустойчивости, вызванные вращающимся потоком пыли // Физика плазмы. - 2010. - Т. 36. - № 12 - С. 1098-1103.
9. Дубинов А.Е. Нелинейная теория электростатических волн в пылевой плазме/ А.Е. Дубинов, М.А. Сазонкин // Вопросы Атомной науки и техники. Серия: Теоретическая и прикладная физика. - 2011. - № 1-2. - С. 77-97.
10. Захаров В.Ю. Анализ устойчивости однородного состояния магнитоактивной плазмы, содержащей малоподвижные пылевые частицы / В.Ю. Захаров, Т.Г. Чернова // Успехи современной науки и образования. - 2017. - Т. 5. - С.155-158.

Список литературы на английском языке / References in English

1. Kuvshinov B.N. Magnetohydrodynamic model for plasma instabilities in the ion-kinetic regime / B.N. Kuvshinov // Plasma Phys. Control. Fusion. - 1994. - V.l. - № 9. - P. 2882-2889.
2. Fortov V. E. Mechanism of dust-acoustic instability in a direct current glow discharge plasma / V. E. Fortov, A. G. Khrapak, S. A. Khrapak and others // Physics of Plasmas.- 2000.- V.7.- № 5.- P. 1374-1380.
3. Fortov V. E. Fizika neideal'noj plazmy [Physics of nonideal plasma] / V.E. Fortov, A. G. Khrapak, I. T.Yakubov. - M.: Fizmatlit, 2004.- 528 p. [in Russian]
4. Shukla P.K. Low-frequency electromagnetic waves in a Hall-magnetohydrodynamic plasma with charged dust macroparticles / P.K. Shukla, I. Kourakis, L. Stenflo // Phys.Plasmas. -2005.- V.12.- P. 024501-1-4.
5. Shukla P.K. New Generalized Dispersion Relation for Low-Frequency Electromagnetic Waves in a Hall-Magnetohydrodynamic Dusty Plasmas / P.K. Shukla, I. Kourakis, L. Stenflo // New vistas in dusty plasmas. Fourth International Conference on the Physics of Dusty Plasmas. Orleans. France. 13-17 June.2005 / Springer, 2005.- V. 799.- P. 311-314.
6. Prudskikh V.V. Acceleration of dust particles by low-frequency Alfven waves / V.V. Prudskikh, Yu.A. Shchekinov // Physics Letters A.- 2008.- V. 372.- P. 2671-2675.
7. Prudskikh V.V. Mirror instability in a plasma with cold gyrating dust particles / V.V. Prudskikh, L.V. Kostyukova, Yu.A. Shchekinov // Phys. Plasmas.- 2010.- V. 17.- P.033701.
8. Prudskikh V. V. Nizkochastotnye elektromagnitnye neustojchivosti, vyzvannye vrashhajushhimsja potokom pyli [Low-frequency electromagnetic instabilities caused by a rotating dust flow ] / V.V. Prudskikh // Fizika plazmy [Plasma Physics].- 2010.-V. 36.- № 12.-P. 1098-1103. [in Russian]
9. Dubinov A. E. Nelinejnaja teorija jelektrostaticheskih voln v pylevoj plazme [Nonlinear theory of electrostatic waves in dust plasma] / A. E. Dubinov, M. A. Sazonkin // Voprosy Atomnoj nauki i tehniki. Serija: Teoreticheskaja i prikladnaja fizika [Problems of Atomic science and technology. Series: Theoretical and applied physics].- 2011.- № 1-2.- P. 77-97. [in Russian]
10. Zakharov V. Yu. Analiz ustojchivosti odnorodnogo sostojanija magnitoaktivnoj plazmy, soderzhashhej malopodvizhnye pylevye chasticy [Analysis of the stability of homogeneous  magnetized dusty plasma] / V. Yu. Zakharov, T. G. Chernova // Uspehi sovremennoj nauki i obrazovanija [Advances in modern science and education]. -2017.- V. 5.- P. 155-158. [in Russian]