РЕШЕНИЕ ПРОСТРАНСТВЕННЫХ СТЕРЖНЕВЫХ СИСТЕМ С БОЛЬШИМИ ПЕРЕМЕЩЕНИЯМИ УЗЛОВ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ В СМЕШАННОЙ ФОРМЕ

Курочкина И.В.¹, Милохова В.И.², Мокшанова Р.А.³, Воронкова Г.В.⁴

¹Магистр, Волгоградский государственный технический университет, ²Магистр, Волгоградский государственный технический университет, ³Магистр, Волгоградский государственный технический университет, ⁴ORCID: 0000-0001-5837-3895, Кандидат технических наук, доцент, Волгоградский государственный технический университет

РЕШЕНИЕ ПРОСТРАНСТВЕННЫХ СТЕРЖНЕВЫХ СИСТЕМ С БОЛЬШИМИ ПЕРЕМЕЩЕНИЯМИ УЗЛОВ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ В СМЕШАННОЙ ФОРМЕ

Аннотация

В статье приведена методика расчета систем с односторонними связями по методу конечных элементов в форме классического смешанного метода. Описан подход к формированию системы разрешающих уравнений, получающихся непосредственно из статических и кинематических условий и условий неразрывности, для пространственных стержневых систем с большими перемещениями узлов, основанный на процедуре пошагового догружения и выполнения расчета в линейной постановке на каждом шаге с учетом новой геометрии системы, достигнутой на предыдущем шаге.

Ключевые слова: метод конечных элементов, классический смешанный метод, геометрическая нелинейность, шарнирно-стержневая система.

Kurochkina I.V.¹, Milokhova V.I.², Mokshanova R.A.³, Voronkova G.V.⁴

¹Graduate Student, Volgograd State Technical University, ²Graduate Student, Volgograd State Technical University, ³Graduate Student, Volgograd State Technical University, ⁴ORCID: 0000-0001-5837-3895, PhD in Engineering, Associate Professor, Volgograd State Technical University

SOLUTION OF SPATIAL FRAME STRUCTURE WITH LARGE NODE DISPLACEMENTS BY FINITE ELEMENTS METHOD IN A MIXED FORM

Abstract

The article contains the method of system calculation with unilateral links by the finite element method in the form of a classical mixed method. We described an approach to the formation of a system of resolving equations obtained directly from static and kinematic conditions and continuity conditions for spatial frame structures with large node displacements based on the stepwise pre-loading procedure and the calculation in a linear setting at each step with regard to the new system geometry achieved at the previous step.

Keywords: finite element method, classical mixed method, geometrical nonlinearity, hinge-rod system.

С развитием компьютерной техники и технологии широкое развитие в расчетах строительных конструкций получил метод конечных элементов. Наиболее часто этот метод реализуется в форме метода перемещений, но, как показано в работе [7], при решении задач в нелинейной постановке данная форма дает большие расхождения с точными решениями. В таких задачах более точные решения позволяет получить метод конечных элементов в форме смешанного метода. Для стержневых конечных элементов в основной системе смешанного метода принимаются одновременно как усилия, так и перемещения [5]. Ввиду простоты основной системы элементы матрицы откликов получаются непосредственно из статических и кинематических условий и условий неразрывности.

Рассмотрим применение метода конечных элементов в смешанной форме для расчета вантовой конструкции. Будем рассматривать схему в виде верхнего абсолютно жесткого тела, опертого на колонну. Нижнее кольцо подвешено на тросах к верхнему диску. Для удобства теоретических выкладок необходимо представить нижнее кольцо в виде полигонального многоугольника, вписанного в окружность. В данной задаче принят гексагональный многоугольник.

Для составления системы разрешающих уравнений рассмотрим узел симметричной конструкции с примыкающими к нему стержнями. Фрагмент основной системы смешанного метода показан на рис.1.

На данном рисунке точка О является центром нижнего кольца с радиусом R, i – рассматриваемый узел нижнего кольца, i’ –узел верхнего кольца.

Такая система кинематически и геометрически изменяемая и может сохранять свою геометрическую конфигурацию только при самоуравновешенной нагрузке статически эквивалентной нулю.

Как и нить с припуском (геометрически изменяемую систему), рассматриваемую систему нужно сначала рассчитать как систему из нерастяжимых элементов, чтобы найти её равновесную конфигурацию под заданной узловой нагрузкой.

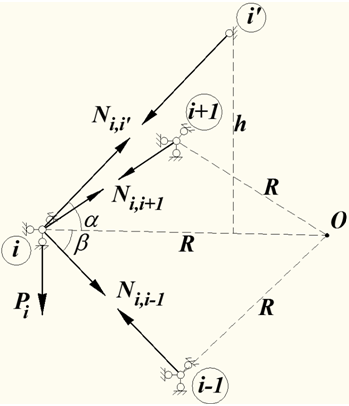
Рис. 1 – Фрагмент основной системы смешанного метода

 

Рассмотрим составление уравнений равновесия в общем виде.

Условия статического равновесия узла i:

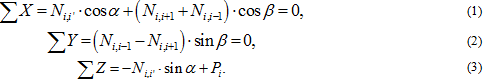
Из (3) получаем, что 

Из (2) следует, что 

Тогда, подставляя полученные значения (4) и (5) в (1), получаем

Это выражение показывает, что усилия в элементах кольца, примыкающих к i-тому узлу – равны между собой и зависят только от нагрузки приложенной в узле P_i. При переходе к другому узлу, то есть к i+1 или к i-1 получаем другие усилия, что является противоречием. Это противоречие устраняется при условии P_i=P=const, тогда кольцо оказывается равномерно сжатым и усилия во всех тросах будут также одинаковыми.

Для получения решения этой задачи при разных значениях узловой нагрузки P_i необходимо перейти к решению задачи в нелинейной постановке. При этом полученное в линейной постановке решение по недеформируемой схеме может быть использовано в качестве начального приближения в итерационном процессе.

Как только к узлам будут приложены дополнительные неодинаковые нагрузки ΔP_i, система изменит конфигурацию и все её узлы сместятся на величины Δx_i, Δy_i, Δz_i, [6]. Этими величинами будет определяться положение каждого стержня в пространстве. Найдём величины Δx_i, Δy_i, Δz_i в зависимости от узловых нагрузок ΔP_i+ ΔP_i для системы из недеформируемых стержней.

Основная система смешанного метода получается введением в каждый незакреплённый узел i (i=1, …., 6) по три связи, препятствующие линейным перемещениям узла по направлению локальных осей координат и устранением связей в разрезе каждого из стержней системы. Таким образом, в основной системе имеем 30 неизвестных: 12 силовых неизвестных ( по числу стержней) и 18 кинематических неизвестных (по три неизвестных в каждом закрепленном узле). В соответствии с этим система разрешающих уравнений в линейной постановке задачи будет состоять из 30 уравнений.

Для дальнейших вычислений введём следующие обозначения и допущения в соответствие с работой [3]. Примем нумерацию узлов нижнего кольца арабскими цифрами от 1 до 6, а нумерацию узлов верхнего кольца от 1¢ до 6¢. Стержни вант, соединяющие верхнее и нижнее кольца, имеют нумерацию от 1-1¢ до 6-6¢. Геометрические параметры системы:

l_1¢-1 = l_2¢-2 = l_3¢-3 = l_4¢-4 = l_5¢-5 = l_6¢-6 = l₁ - длины радиальных нитей; l_1-2 = l_2-3 = l_3-4 = l_4-5 = l_5-6 = l_6-1 = l - длины сторон шестиугольника;

- углы наклона радиальных нитей в деформированном состоянии к плоскости xOy к оси z в локальной системе координат узла;

- углы между проекцией деформированной нити на плоскость xOy и осью x.

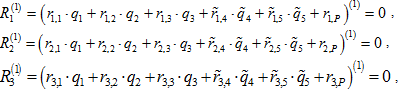Для нитей сторон шестиугольника приняты те же обозначения, но с нижним индексом 2. Возникающие реакции  разрывы в разрезе  неизвестные перемещения  усилия  Запишем разрешающие уравнения для узла 1 в линейной постановке:    (6) Уравнения неразрывности деформаций в разрезе:

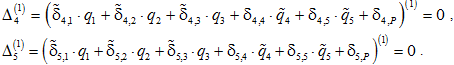
Для системы с отклонениями от заданной геометрии (рис.2) составим уравнения статического равновесия и геометрические уравнения в локальных системах координат. На рис.2 показано перемещение наклонного стержня 1'‑1 в новое положение, вызванное смещением узла 1 на величины Δx, Δy, Δz.

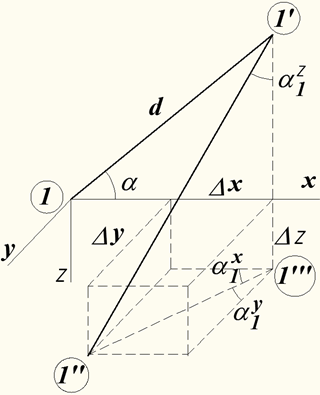
Рис. 2 – Перемещение стержня 1'‑1

Из геометрических соотношений следует: Отсюда после образования получаем:

Необходимые для дальнейших выкладок величины узлов ориентации стержня 1'‑1 в новом отклоненном положении определяются следующими выражениями:

Аналогично находим для стержней 1-2 и 6-1 где   - перемещение узла 1 в его локальной системе координат,   - перемещение узла 2 в локальной системе координат. где 

При смещении узла 1 в новое положение под воздействием нагрузки со смещениями по осям координат:

Новая длина нити 1-1’ будет определяться выражением

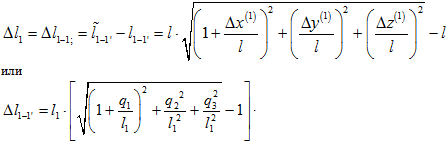Приращение длины: Приращение длины выражается через усилие в нити, Угол наклона деформированной нити к горизонтальной плоскости xOy:

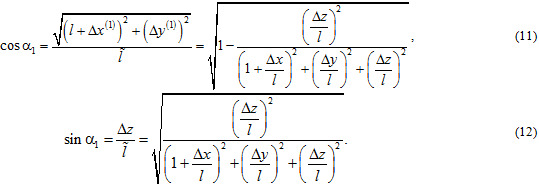
В дальнейших выкладках использование выражений типа (11) и (12) для составления разрешающих уравнений и их последующего решения интеграционным способом оказывается неудобным. Так как в расчетах можно ограничиваться в первом приближении только величинами первого порядка малости, то формально можно разложить функцию  в ряд Тейлора с удержанием в нём только величин первого порядка малости.

Для нити между узлами 1 и 2 в системе координат, принятой для узла 1 стержня 1'‑1, перемещения её концов в системе координат xOy находятся с использованием зависимостей:

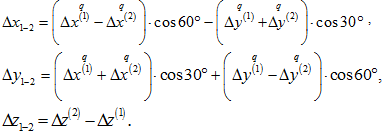
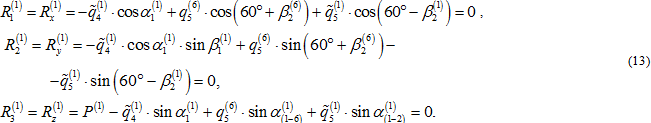В отклоненном положении условия равновесия (1) узла 1 принимают следующий вид: Уравнения совместности (неразрывности) деформации:

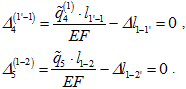
Уравнения для остальных узлов полигонального кольца получаются циклически.

Решение нелинейной системы уравнений (13) выполняется по алгоритму изложенному [1]. Он заключается в пошаговом нагружении конструкции, линейном расчете на каждом шаге догружения и итерационном уточнении линейного решения. Уточнение решения на каждом шаге выполняется интегрированием суммы решений на всех этапах расчета.

Правильность полученного решения можно проверить, используя вме- сто силового воздействия кинематическое воздействие в виде управляемого перемещения узла. Методика расчета по методу конечных элементов в форме классического смешанного метода позволяет делать это на любом шаге нагружения изменением вида параметра нагружения.

Список литературы / References

1. Габова В.В. Алгоритм формирования глобальной матрицы откликов плоской стержневой системы / А. В. Игнатьев, В. В. Габова // Вестник Волгоградского государственного архитектурно-строительного университета. Серия: Строительство и архитектура. – 2009. – № 14. – С. 71.
2. Габова В.В. Получение матрицы откликов стержневого конечного элемента плоской стержневой системы на основе смешанного вариационного принципа / А. В. Игнатьев, В. В. Габова // Вестник Волгоградского государственного архитектурно-строительного университета. Серия: Строительство и архитектура. – 2009. – № 14. – С. 75-79.
3. Габова В.В. Влияния нумерации узлов и элементов основной системы на структуру глобальной матрицы откликов и результаты расчета при численной реализации алгоритма статического расчета плоских стержневых систем по МКЭ в смешанной форме / В. В. Габова //Интернет-Вестник ВолгГАСУ. – 2008. – № 3 (6). – С. 4.
4. Игнатьев В.А. Решение геометрически нелинейных задач статики шарнирно-стержневых систем на основе метода конечных элементов в форме классического смешанного метода / А. В. Игнатьев, В. А. Игнатьев, Е. В. Онищенко // Вестник МГСУ. – 2016. – № 2. – С. 20-33.
5. Игнатьев А.В. Расчет геометрически нелинейных плоских шарнирно-стержневых систем по методу конечных элементов в форме классического смешанного метода / А. В. Игнатьев, В. А. Игнатьев // Вестник Волгоградского государственного архитектурно-строительного университета. Серия: Строительство и архитектура. 2013. № 34 (53). С. 82-89.
6. Рекунов С.С. Формирование матриц откликов конечных элементов с учётом упругого основания / С. С. Рекунов // Интернет-журнал «Науковедение». – 2014. – № 5 (24). – С. 56.

Список литературы на английском языке / References in English

1. Gabova V.V. Algoritm formirovaniya global'noy matritsy otklikov ploskoy sterzhnevoy sistemy [An algorithm for generating global response matrices for 2-D framed systems] / A. V. Ignat'ev, V. V. Gabova // Vestnik Volgogradskogo gosudarstvennogo arkhitekturno-stroitel'nogo universiteta. Seriya: Stroitel'stvo i arkhitektura [Bulletin of the VSUACE. Series: Civil Engineering and Architecture]. – 2009. – № 14. – pp. 71-74. [in Russian]
2. Gabova V.V. Poluchenie matritsy otklikov sterzhnevogo konechnogo elementa ploskoy sterzhnevoy sistemy na osnove smeshannogo variatsionnogo printsipa [Generating a response matrix of a 2-D frame finite element using the mixed variational principle] / A. V. Ignat'ev, V. V. Gabova // Vestnik Volgogradskogo gosudarstvennogo arkhitekturno-stroitel'nogo universiteta. Seriya: Stroitel'stvo i arkhitektura [Bulletin of the VSUACE. Series: Civil Engineering and Architecture]. – 2009. – № 14. – pp. 75-79. [in Russian]
3. Gabova V.V. Vliyaniya numeratsii uzlov i elementov osnovnoy sistemy na strukturu global'noy matritsy otklikov i rezul'taty rascheta pri chislennoy realizatsii algoritma staticheskogo rascheta ploskikh sterzhnevykh sistem po MKE v smeshannoy forme [Influence of the numeration of the main system's nodes and elements on the structure of the global response matrix, and the computation results of numerical implementation of the static analysis algorithm for plane rod systems applying the mixed form of FEM] / V. V. Gabova //Internet-Vestnik VolgGASU. – 2008. – № 3 (6). – p. 4. [in Russian]
4. Ignat'ev V.A. Reshenie geometricheski nelineynykh zadach statiki sharnirno-sterzhnevykh sistem na osnove metoda konechnykh elementov v forme klassicheskogo smeshannogo metoda [Solving geometrically nonlinear tasks of the statics of hinged-rod systems basing on finite element method in the form of classical mixed method] / A. V. Ignat'ev, V. A. Ignat'ev, E. V. Onishchenko // Vestnik MGSU. – 2016. – № 2. – pp. 20-33. [in Russian]
5. Ignat'ev A.V. Raschet geometricheski nelineynykh ploskikh sharnirno-sterzhnevykh sistem po metodu konechnykh elementov v forme klassicheskogo smeshannogo metoda [Calculation of geometrically nonlinear flat hinged and frame systems by the finite element method in the form of the classical mixed method] / A. V. Ignat'ev, V. A. Ignat'ev // Vestnik Volgogradskogo gosudarstvennogo arkhitekturno-stroitel'nogo universiteta. Seriya: Stroitel'stvo i arkhitektura [Bulletin of the VSUACE. Series: Civil Engineering and Architecture]. 2013. № 34 (53). pp. 82-89. [in Russian]
6. Rekunov S.S. Formirovanie matrits otklikov konechnykh elementov s uchetom uprugogo osnovaniya [Forming the matrix of responses of the finite elements taking into account the elastic base] / S. S. Rekunov // Internet-zhurnal «Naukovedenie» [Internet magazine «Naukovedenie»]. – 2014. – № 5 (24). – p. 56. [in Russian]