РАСПОЗНАВАНИЕ ПРИРОДНЫХ ОБЪЕКТОВ С ФРАКТАЛЬНОЙ ПОВЕРХНОСТЬЮ

Маяцкая И.А.

ORCID: 0000-0003-1530-8238, Кандидат технических наук, Донской государственный технический университет в г. Ростове-на-Дону

РАСПОЗНАВАНИЕ ПРИРОДНЫХ ОБЪЕКТОВ С ФРАКТАЛЬНОЙ ПОВЕРХНОСТЬЮ

Аннотация

Данное исследование посвящено проблеме распознавания растительных объектов, имеющих фрактальную поверхность. Одним из направлений исследований является разработка недорогих датчиков, способных мгновенно распознать конкретные компоненты растительного материала, имеющие неровную поверхность объекта. Большое внимание уделено моделированию объектов и математическим методам распознавания. Предлагается математическая база для нового подхода к анализу и проектированию технологических процессов переработки сельскохозяйственных культур. Рассматривается проблема распознавания растительных объектов, близких по форме к реальным, по теневому контуру.

Ключевые слова: модель, растительный объект, датчик, фрактал, контур.

Mayatskaya I.A.

ORCID: 0000-0003-1530-8238, PhD in Engineering, Don State Technical University, Rostov-on-Don

RECOGNITION OF NATURAL OBJECTS WITH FRACTAL SURFACE

Abstract

This research is devoted to the problem of recognition of vegetal objects with a fractal surface. One of the areas of this research is the development of inexpensive sensors capable of instantly recognizing specific components of vegetal material with an uneven surface of the object. Much attention is paid to object modeling and mathematical recognition methods. The mathematical base for a new approach to the analysis and design of technological processes of agricultural crop processing is proposed. The problem of recognition of vegetal objects which are close in shape to the real ones in the shadow contour is considered.

Keywords: model, vegetal object, sensor, fractal, contour.

Данное исследование посвящено проблеме распознавания растительных объектов, имеющих фрактальную поверхность. Одним из направлений исследований является разработка недорогих датчиков, способных мгновенно распознать конкретные компоненты растительного материала, имеющие неровную сложную форму [1, С. 862], [2, С. 866]. При распознавании растительного объекта используются оптические датчики, которые сканируют объект. Рассмотрим методику распознавания растительного объекта с помощью теневого контура. Она основана на построении огибающей к семейству кривых полученных сечением плоскостью, перпендикулярной направлению  оптического потока. Рассмотрим  модель, для которой уравнение  поверхности этого объекта в неподвижной системе имеет вид:  . В подвижной системе координат уравнение поверхности объекта будет иметь следующий вид:   (1)

Оптический поток направлен по оси OY. Теневой контур объекта получается с помощью построения огибающей к семейству  кривых (Y=C). Для этого нужно решить систему уравнений:

  (2)

В результате получаем уравнение, которое описывает теневой контур и  имеет форму эллипса, но его параметры уже другие.  Предложенная методика позволит получить теневой контур растительного объекта. Можно отметить, что этот контур представляет собой замкнутую кривую и он искажается, если учесть, что объект движется в пространстве, что тоже можно учесть.

В реальности исходный контур  может иметь контур в виде ломанных линий. В этом случае нужно использовать методы фрактальной геометрии, определить фрактальную размерность объекта.

Использование разработанных моделей при распознавании образов растительных объектов позволит повысить эффективность работы роботизированных средств механизации. Если же нужно учитывать геометрические параметры конкретного растительного объекта, то необходимо выяснить, насколько данная модель растительного объекта близка к реальному объекту [3, С. 346].

В природе существуют и другие объекты, имеющие фрактальную поверхность [4, С. 5]. На рис. 1 и 2 представлены такие объекты, которые имеют шероховатость, искривление линии контура, отдельные тела на поверхности. Распознавание таких объектов происходит с помощью фото и видеосъемки, но распознать объект можно по отдельному фрагменту (фрактально) поверхности, который типичен только для этого объекта с помощью оптических датчиков. Необходимо изучение характерных особенностей конкретного природного объекта.

Рис. 1 – Фрактальная поверхность с небольшой размерностью: а – природная каменная плита; б – кора дерева

Рис. 2 – Фрактальная поверхность с очень большой размерностью: а – береговая линия; б – острые камни на холме

 

Задача о математическом моделировании природных объектов и процессов (например, береговой линии, строения растений, распознавание объекта сложной геометрической формы) является актуальной. В работах [3, С. 346], [6].  рассматривается возможность моделирования природных объектов с помощью фрактальной геометрии и теории графов. Такой подход позволяет получить не только математическое описание объектов и процессов, но и дает возможность для графического моделирования. Для этого используют системы итерируемых функций.

Данный метод построения моделей растительных объектов подразумевает использование систем итеративных функций, который может быть описан как последовательный итеративный расчет координат новых точек в пространстве:  - функции преобразования координат, которые определяют форму фрактала. В результате получаем фрактальную модель объекта.  От количества итераций зависит структура модели. В статье [3, С. 346] показаны конкретные модели для различных типов их ветвления.

В фрактальной геометрии широко используются фракталы со свойством самоподобия. Именно такие типы рассмотрены в работе [7, С. 6]. На рис. 3 показаны растительные объекты, обладающие этим свойством, только с различной фрактальной размерностью, связанной с количеством итераций.

Рис. 3 – Модели листостебельных растений, построенные с помощью систем итеративных функций (число итераций: а – n=4; б –n=6; а – n=10;)

 

Для фракталов, не обладающих свойством самоподобия, например, береговая линия или поверхность, которая меняет свою поверхность с течением времени (рис. 4), найти размерность достаточно сложно.

Рис. 4 – Фрактальная поверхность (динамическая модель): а – поверхность водяной поверхности фонтана; б – горная поверхность

 

Для описания фрактальной модели нужно прежде всего установить зависимость между конечным результатом и задаваемой начальной структуры растения, т. е. динамический закон . Найти эту зависимость бывает очень сложно.

Проведя анализ различных фрактальных объектов, можно сказать, что есть шероховатость поверхность,  искривление линии, объемные тела, непрерывно и  динамично развивающие, отдельные тела на поверхности, теневой контур. Именно последний объект рассматривается далее.

Распознать фрактальный объект достаточно трудно. Направление отраженного оптического луча зависит от кривизны определяемого объекта. Если объект имеет выпуклую шаровую поверхность, то радиус кривизны ρ=R; если же вогнутую, то ρ=˗R; если поверхность плоская, то ρ=∞. Для вогнутых поверхностей труднее всего создать метод определения самой поверхности. Также трудности возникают при определении поверхности, динамически изменяющейся во времени. В этом случае можно построить осредненную поверхность, и тогда определять ее.

Использование методов фрактальной геометрии позволяет создавать графические модели. Зная математическое описание модели объекта, можно определить методику распознавания: по всему контуру, определяемому некоторой функции; по части контура, который имеет характерные особенности только для данного объекта; по структуре распознаваемого объекта.

Так, для первого метода можно использовать методику получения теневого контура, полученного с помощью теории огибающих.

Рассмотрим методику распознавания растительного объекта с помощью теневого контура. Она основана на построении огибающей к семейству кривых полученных сечением плоскостью, перпендикулярной направлению  оптического потока.

Рассмотрим следующие модели: эллипсоид вращения

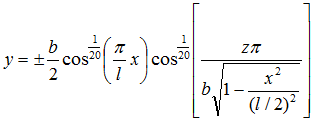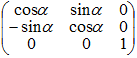      (2) цилиндр, который можно описать чечевицеобразной моделью при n=20,    (3) Рассмотрим  поворот тела относительно оси Сz:     (4) Матрица преобразования имеет следующий вид:    (5)

Оптический поток направлен по оси OY. Теневой контур объекта получается с помощью построения огибающей к семейству  кривых ( ). Для этого нужно решить систему уравнений (1).

В результате получаем следующие системы уравнений: эллипсоид вращения

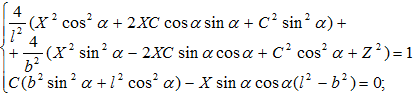   (6)

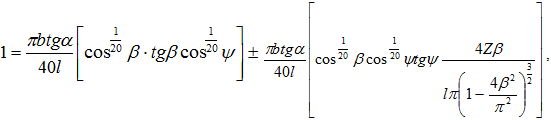цилиндр  -     (7) где 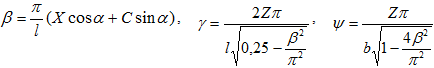   (8) Решая систему уравнений (7), получаем уравнение теневого контура: 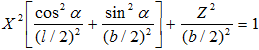  (9)

Площадь теневого контура эллипсоида вращения, который представляет собой эллипс, определяется по формуле: , где  A и B определяются выражениями: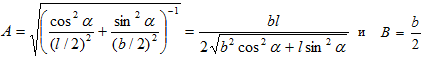

Площадь теневого контура для модели в виде цилиндра можно найти по формуле , при этом выполняется условие  . Параметр d определяется по формулам:

Для второго метода можно использовать методику оценки фрактальности поверхности с помощью построения первой производной и второй производной к контуру в заданной плоскости или по характеру изменения изогнутости поверхности, по точкам экстремума и точкам перегиба, характерным именно для данного контура.

При распознавании можно использовать и другие разделы математики, например, теорию графов. Эта теория может быть использована в третьем методе. В связи с этим объект можно оценивать по формализованному описанию объекта, например, по структуре растительного объекта.

Для этого надо построить модель объекта в виде графа, можно использовать ориентированный граф, различные деревья и сети [6, С. 21;, 61, 449]. В настоящее время   хорошо изучены современные компьютерные технологии, связанные с применением теории графов. Математические модели, методы и алгоритмы прикладной теории графов позволяют строить модели природных объектов, проводить оптимизацию.

Итак, необходимо определить структурные закономерности, которые позволят решать задачи поиска решающих функций и другие задачи распознавания. При этом надо ориентировать лишь на сам факт наличия структурных закономерностей объекта, не описывая его в целом. Именно такой поход наиболее оптимальный.

Список литературы / References

1. Демченко Б.М., Маяцкая И.А. Распознавание объектов и модели растительных материалов / Б.М. Демченко, И.А. Маяцкая // Научное обозрение. – 2014. –№7-3. – С. 862–865.
2. Демченко Б.М., Маяцкая И.А. Определение теневого контура при распознавании растительных объектов / Б.М. Демченко, И.А. Маяцкая // Научное обозрение. – 2014. –№7-3. – С. 866–868.
3. Маяцкая И.А., Демченко Б.М. Аналитическая интерпретация моделей растительных материалов / И.А. Маяцкая, Б.М. Демченко // Вестник Волгоградского государственного архитектурно-строительного университета. Серия: Строительство и архитектура. – 2013. –№30. – С. 346–351.
4. МандельбротБ. Фрактальная геометрия природы / Б.  Мандельброт . – М. : Издательство Институт компьютерных исследований. –2002. – 656 c.
5. Маяцкая И.А., Краснобаев И.А. Моделирование листостебельных материалов с помощью теории графов [Электронный ресурс] // Инженерный вестник Дона: электрон. науч.-инновац. журн. — 2012. — №4, часть 2.
6. Касьянов В.Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение / В.Н. Касьянов, В.А. Евстигнеев. – СПб. : БХВ-Петербург. –2003. – 1104 c.
7. Кроновер Р.М. Фракталы и хаос в динамических системах / Р.М. Кроновер. – М.: Техносфера. –2006. – 488 c.

Список литературы на английском языке / References in English

1. Demchenko, Mayatskaya I.A. Raspoznavaniye obektov I modeli rastitelnykh materialov [Recognition of objects and models of plant materials] / B.M. Demchenko, I.A. Mayatskaya // Nauchnoye obozreniye [Scientific Review]. – 2014. №7-3. P. 862–865. [in Russian]
2. Demchenko B.M., Mayatskaya I.A. Opredeleniye tenevogo kontura pri raspoznavaniye  rastitelnykh obektov [Determining the shadow path when recognizing plant objects] / B.M. Demchenko, I.A. Mayatskaya // Nauchnoye obozreniye [Scientific Review]. – 2014. №7-3. P. 866–868. [in Russian]
3. Mayatskaya I.A., Demchenko B.M. Analiticheskaya interpretatsiya modeley rastitelnykh materialov [Analytical interpretation of models of plant materials] / I.A. Mayatskaya, B.M. Demchenko // Vestnik VolgGASU, seriya Stroitelstvo i arkhitektura [Bulletin of the Volgograd State Architectural and Construction University. Series: Building and architecture.]. – 2013. №30. P. 346–351. [in Russian]
4. Mandelbrot B. Fraktalnaya geometriya prirody [Fractal Geometry of Nature] / B.Mandelbrot. – M. : Izdatelstvo Institut kompyuternykh issledovaniy. – 2002. – 656 p. [in Russian]
5. Mayatskaya I.A., Krasnobaev I.A. Modelirovaniye listostebelnykh materialov s pomoshchyu  teorii grafov [Modeling of leaf-stem materials using the theory of graphs [Electronic resource]] / I.A. Mayatskaya , I.A. Krasnobaev // Ingenernyi  vestnik Dona [The engineer's messenger of the Don: electron. nauk.-innov. journal.]. – 2014. – №4-2. [in Russian]
6. Kasyanov V.N., Evstigneev V.A. Grafy v programirovanii: obrabotka, vizualizatsiya i primeneniye [Graphs in programming: processing, visualization and application] / V.N. Kasyanov, V.A. Evstigneev. - St. Petersburg. : BHV-Petersburg. -2003. – 1104 p. [in Russian]
7. Kronover R.M. Fraktaly i khaos v dinamicheskikh sistemakh [Fractals and chaos in dynamic systems] / R.M. Kronover. – M.: Tekhnosfera. –2006. – 488 p. [in Russian]