ПРИМЕНЕНИЕ АЛГОРИТМОВ КЛАСТЕРИЗАЦИИ K-MEANS И G-MEANS В ЗАДАЧАХ РАСПОЗНАВАНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ

Антропов В.В.

ORCID: 0000-0002-8019-5164, аспирант, Санкт-Петербургский Горный университет

ПРИМЕНЕНИЕ АЛГОРИТМОВ КЛАСТЕРИЗАЦИИ K-MEANS И G-MEANS В ЗАДАЧАХ РАСПОЗНАВАНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ

Аннотация

Рассмотрено применение кластеризации семействами алгоритмов k-means и g-means в задачах распознавания воздушных объектов в условиях неполноты и недостоверности данных. Обоснован выбор этих алгоритмов кластеризации. Подчёркнута важность кластеризации в задачах распознавания. Сформирована исследовательская выборка, которая применялась для демонстрации работоспособности кластеризации семействами алгоритмов k-means и g-means. Проведён анализ результатов, полученных в ходе кластеризации. Выявлена перспектива методики прогнозирования в задачах распознавания ВО.

Ключевые слова: воздушные объекты, распознавание, радиолокационное распознавание, кластеризация, кластеризации k-means и g-means.

Antropov V.V.

ORCID: 0000-0002-8019-5164, Postgraduate Student, St. Petersburg Mining University

APPLICATION OF K-MEANS AND G-MEANS CLUSTERING ALGORITHMS IN OBJECTS RECOGNITION

Abstract

The application of clustering by families of k-means and g-means algorithms in problems of recognition of airborne objects under the conditions of incompleteness and unreliability of data is considered in the article. The choice of these clustering algorithms is substantiated. The importance of clustering in recognition problems is emphasized. A research sample was created and used to demonstrate the efficiency of clustering by families of k-means and g-means algorithms. The analysis of the results obtained during clustering is carried out. The perspective of the forecasting method in problems of airborne objects recognition is revealed.

Keywords: airborne objects, recognition, radar detection, clustering, k-means and g-means clustering.

В современных реалиях, при значительном возрастании роли авиации, стали возникать проблемы, связанные с контролем воздушной обстановки, при решении задач логистики, безопасности и пр. В связи с этим, остро стоит задача оперативной обработки информации, связанной с распознаванием типов летательных аппаратов, находящихся в воздушном пространстве, и возможных вариантов их действий.

Распознавание воздушных объектов имеет ряд трудностей, такие как неполнота информации, её недостоверность, и пр. Распознавание производится по ряду признаков, в результате чего мы с высокой долей вероятности, либо с полной уверенностью (это зависит от методики распознавания), можем определить принадлежность исследуемого нами воздушного объекта тому или другому типу, или даже можем назвать модель воздушного судна.

Методики распознавания условно можно разделить на визуальные, траекторные и радиолокационные. Наиболее точными являются методики радиолокационного распознавания.

Распознавание воздушных объектов можно разделить на несколько этапов:

• Селекция целей на фоне помех;
• Классификация целей;
• Опознавание целей;
• Оценка состояния и контроль действий целей.

Для реализации распознавания необходимо достаточно точно определить, какие классы воздушных объектов можно определить. Для этого в работе были исследованы алгоритмы кластеризации k-means и g-means.

Кластеризация семействами алгоритмов k-means и g-means обычно используется для решения задач описательной бизнес-аналитики, в частности, для кластеризации (автоматизированной сегментации) объектов. Данный тип кластеризации показал высокую степень надёжности и перспективы дальнейшей высокопроизводительной обработки информации, применить методы прогнозирования, что открывает ещё большие возможности для анализа данных.

Принцип оптимального разбиения множества данных на k кластеров является основной составляющей алгоритма k-means. Пока целевая функция алгоритма разбиения не достигнет экстремума, алгоритм будет пытаться группировать данные по кластерам. Количество кластеров k задаётся аналитиком, исходя из его предпочтений, опирающихся на его интуицию, практический опыт, теоретическую составляющую и пр. Важной составляющей алгоритма является центр кластера – среднее значения переменных объектов, входящих в кластер. Алгоритм состоит из двух этапов.

1. Первоначальное распределение объектов по кластерам. Аналитик задает количество кластеров, по которым будут распределяться объекты из исследовательской выборки. Средство, применяемое аналитиком, произвольным образом выбирает количество объектов из исследуемой выборки равное количеству, заданных аналитиком кластеров, и приравнивает значения центров этих кластеров к значениям выбранных объектов. Таким образом, каждый кластер получит свой начальный центр.
2. Итерационный процесс. Теперь алгоритм высчитывает новые центры кластеров и распределяет по кластерам объекты из исследовательской выборки. Работа алгоритма продолжается до тех пор, пока значения центров кластеров не перестанут пересчитываться, т.е. пока все объекты из исследовательской выборки не перестанут менять кластер, к которому их отнес алгоритм на предыдущем шаге вычислений.

Случается, что аналитик не имеет возможности назвать точное число кластеров, на которое требуется разбить исследовательскую выборку. В таких случаях применяется алгоритм g-means. Данный алгоритм, последовательно выполняя статистический тест, сам определяет число кластеров в модели. Суть теста состоит в том, что данные внутри каждого кластера подчиняются определенному гауссовскому (Gaussian, отсюда и название алгоритма) закону распределения. Если тест дает отрицательный результат, кластер разбивается на два новых кластера (алгоритмом k-means) с центрами.

Следует обратить внимание, что основой алгоритмов k-means и g-means является гипотеза о компактности, предполагающая, что информацию об объектах из исследовательской выборки, можно представить в виде многомерных векторов,  образующих в пространстве своеобразный комок.[2]

Перед работой алгоритма g-means аналитик должен ввести значения исходного набора данных (X) и уровня значимости (α).

1. На первом шаге C инициализируется как множество центров кластеров средними значениями.
2. 
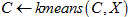
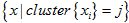3.  набор точек для кластера с центром c_j.
4. Следует проверка гипотезы о том, что значения в каждом кластере j распределены по гауссовскому закону с уровнем значимости α.
5. В случае если тест пройден и распределение является нормальным, то следует запомнить кластер. В противном случае заменить c_j двумя центрами.
6. Пока количество центров не перестанет возрастать, данный алгоритм, будет повторяться.

Формула расстояния между векторами признаков x и y выглядит следующим образом:

, где Z_i - значение значимости.

Теперь находим значимость атрибута по всем кластерам.

1. Вычисляем дисперсию по разбросу между кластерами: 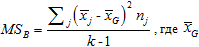 - среднее значение всей исследовательской выборки,  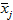- среднее значение в кластере,  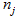- количество объектов, попавших в кластер j, k – количество кластеров.
2. Вычисляем дисперсию по разбросу внутри кластеров:

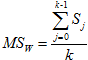, где S_j - СКО внутри кластера.

3. Вычисляем значение F–критерия: .
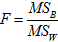4. Вычисляется значимость, Используя функцию распределения Фишера, вычисляем значимость: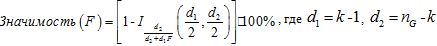, I-неполная бета-функция. [1]

Для дальнейших вычислений мы применим средство Data Mining. Оно позволит наглядно продемонстрировать работу алгоритмов кластеризации на примере работы с воздушными объектами.

Вычисленная нами модель может решить задачу классификации. Кластер присваивает отметку класса на основе большинства принадлежащих ему примеров. Действие алгоритма таково, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров:

, где k – число кластеров,  S_i - полученные кластеры, i = 1, 2, …, k и  μ_i- центры масс векторов .

При подготовке обучающей выборки для кластеризации следует иметь в виду следующее:

 - если задача аналитика – сжато описать имеющиеся данные при помощи кластеров, то выделять тестовую выборку, смысла нет;

- как правило, метрические алгоритмы кластеризации плохо работают с категориальными признаками, измеренными в шкале наименований.

Теперь следует провести нормализацию данных в обучающей выборке. Целью нормализации значений полей является преобразование данных к виду, наиболее подходящему для обработки алгоритмом.

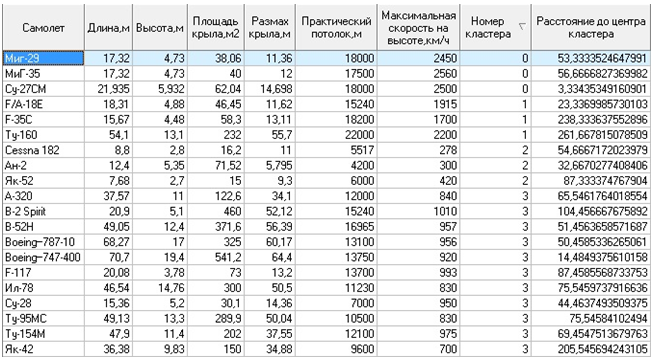
Покажем работоспособность метода на примере информации о воздушных объектах. Для каждого самолёта, кроме его модели, известно шесть характеристик: длина (м), высота (м), площадь крыла (м ), размах крыла (м), практический потолок (м), максимальная скорость на высоте (км/ч). Самолеты можно разбить на сегменты по этим показателям. После отработки алгоритма k-means получим следующие результаты (рис. 1).

Рис. 1 – Общий набор после кластеризации алгоритмом k-means

 

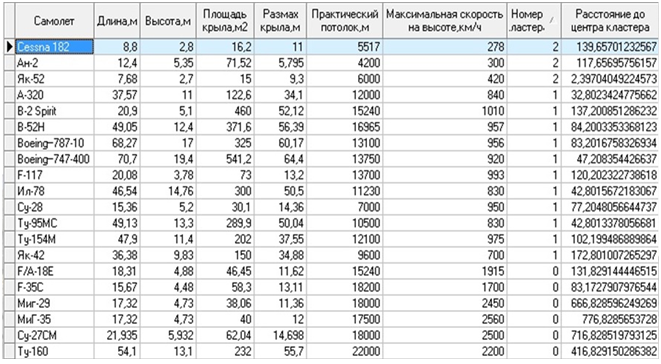
В алгоритме кластеризации g-means у аналитика есть возможность повлиять на результат, используя коэффициент отталкивания, и задать максимальное число кластеров или шагов вручную. Отработав, данный алгоритм выдал результаты, представленные на рис. 2.

Рис. 2 – Общий набор после кластеризации алгоритмом g-means

 

В данной работе были представлены способы кластеризации, которые продемонстрировали интересные результаты, несмотря на то, что количество признаков и объектов в обучающей выборке было крайне мало. Например, в кластеризации g-means получилось разбить воздушные объекты на 3 кластера, которым мы можем дать условные названия, таки как «легкомоторные самолёты», «военные самолёты» и «пассажирские самолёты». Кластеризация k-means продемонстрировала попытку более чёткой кластеризации. В частности это отразилось на разбиении кластера «военной авиации» ещё два.

Оба способа кластеризации показали правильность их выбора, а также наличие высокого потенциала. Добавление дополнительных признаков для распознавания воздушных объектов (фазовый портрет, спектральный портрет, дальностный портрет и пр.) и информации в обучающую выборку (увеличим количество самолётов, которые будем рассматривать) сделает кластеры более точными, а также откроет перспективу для метода прогнозирования, который поможет нам бороться с такими явлениями, как нечёткость информации, её неопределённость, и даже недостоверностью.

Список литературы / References

1. Deductor. Руководство по алгоритмам. Версия 5.2.0. 1995-2010 Компания BaseGroup Labs www.basegroup.ru – 38 с.
2. Лебедев В. В. Информационные технологии бизнес-аналитики. Система подготовки принятия решения Deductor. / В. В. Лебедев, А. И. Дерябин // Учебно-методическое пособие. Кафедра информационных технологий в бизнесе. НИУ ВШЭ ПФб 2011. - 190 с.

Список литературы на английском языке / References in English

1. Deductor. Rukovodstvo po algoritmam. Versiya 5.2.0. [Deductor. Algorithm guide. Version 5.2.0] / 1995-2010 Kompaniya BaseGroup Labs. www.basegroup.ru [1995-2010 BaseGroup  Labs Company. www.basegroup.ru]. – 38 P. [in Russian]
2. Lebedev V. V. Informacionnye technologii biznes-analitiki. Sistema podgotovki prinyatiya resheniya Deductor [Information technology business intelligence. Decision making system Deductor] / V. V. Lebedev, A. I. Deryabin // Uchebno-metodicheskoe posobie. Kafedra informacionnyh tehnogiy v biznese. NIU VSHE PFb [Teaching aid. Department of Information Technologies in Business]. – 2011. –190 P. [in Russian]