НАХОЖДЕНИЕ МИНИМАЛЬНЫХ ОСТОВНЫХ ОРИЕНТИРОВАННЫХ ДЕРЕВЬЕВ

Сдвижков О.А.¹, Мацнев Н.П.²

¹Кандидат физико-математических наук, доцент, Российский государственный университет туризма и сервиса, ²Кандидат технических наук, доцент, Технологический университет, г. Королев

НАХОЖДЕНИЕ МИНИМАЛЬНЫХ ОСТОВНЫХ ОРИЕНТИРОВАННЫХ ДЕРЕВЬЕВ

Аннотация

Рассматривается обобщенная задача о минимальном остовном дереве, то есть задача, в которой матрица весовых коэффициентов дуг, вообще говоря, не является симметричной, решение – ориентированное дерево. В статью вошли математические модели (квадратичного программирования), включая модель с минимальным числом линейных ограничений, к которым сводится обобщенная задача о минимальном остовном дереве. Рассматривается нахождение минимального остовного дерева, когда задан номер корневой, транзитной или висячей вершины, а также случай нескольких условий. Приведены примеры, математические модели решаются средствами программного комплекса Excel.

Ключевые слова: квадратичное программирование, граф, дерево.

Sdvizhkov O.A.¹, Matsnev N.P.²

¹PhD in Physics and Mathematics, Associate Professor, Russian State University of Tourism and Service, ²PhD in Engineering, Associate Professor, Technological University, Korolev

LOCATING MINIMAL FRAMING ORIENTED TREE GRAPHS

Abstract

The article considers a generalized problem of a minimal framing tree graph, that is, a problem with asymmetric matrix of weight coefficients of arcs where the solution is an oriented tree graph. The article includes mathematical models of quadratic programming, including a model with a minimum number of linear constraints the generalized minimal framing tree graph problem is reduced to. We consider finding the minimal framing tree graph when the number of the root, transit, or hanging vertex is given, as well as the case of several conditions. Examples are provided; mathematical models are solved with the help of the Excel.

Keywords: quadratic programming, graph, tree graph.

Введение

Задача о минимальном остовном дереве графа, матрица C весовых коэффициентов дуг которого является симметричной, – классическая задача методов анализа сетей [3], [4], решение ее в Excel рассматривается в [1].

Случай C ≠ C^Т приводит к задаче нахождения минимального ориентированного остовного дерева, сравнимой по сложности с задачей коммивояжера, так как требуется чтобы это дерево не распадалось на несвязные компоненты. Только применение квадратичного программирования позволило построить математические модели этой задачи [5]. Данную работу можно рассматривать как продолжение работы [5].

1. Математические модели задачи о минимальном остовном ориентированном дереве

Следуя [2], будем понимать под ориентированным деревом (ордеревом) ориентированный граф, в котором:

• Существует единственная вершина полустепень захода которой равна 0 – корневая вершина;
• Полустепень захода всех остальных вершин равна 1;
• Каждая вершина достижима из корневой вершины.

Пусть V = {1, 2, . . ., n} – множество вершин, T(V, U) – остовное ордерево, состоящее из дуг (v₁, v₂), (v₃, v₄₎, ... , (v_2k-1, v_2k), … , (v_2(n-1)-1, v_2(n-1)), где ,

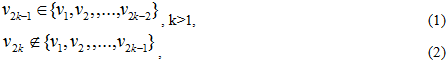
v₁ – номер корневой вершины. Запишем эту последовательность дуг вектором

и поставим ему в соответствие двоичную  матрицу , p=1, 2, …, 2(n-1); j=1,2,…,n, в которой По ней коэффициенты a_ij матрицы смежности ордерева T находятся по формулам:                                                                          (5)

Пусть весовые коэффициенты дуг между вершинами V заданы матрицей С=(с_ij), где i, j = 1, 2, . . ., n, вообще говоря, С^Т≠С. Тогда имеет место следующая теорема.

Теорема 1. Задача нахождения по матрице весовых коэффициентов С минимального остовного ордерева T(V, U) сводится к задаче квадратичного программирования с  двоичными переменными , в которой  целевая функция

коэффициенты a_ij вычисляются по формуле (5), а ограничения записываются в виде:

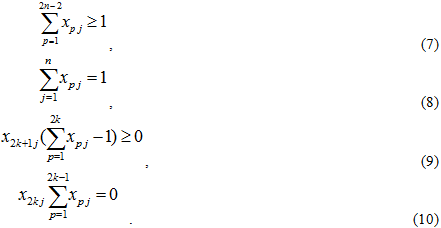
Действительно, в силу (7) ордерево будет содержать все вершины V, условия (8, 9, 10) следуют из (4, 1, 2), соответственно.

Замена квадратичных ограничений (9, 10) линейными ограничениями приводит к следующей теореме.

Теорема 2. Задача нахождения по матрице весовых коэффициентов С минимального остовного ордерева сводится к задаче квадратичного программирования с двоичными переменными , в которой  целевая функция имеет вид (6), ограничения записываются в виде:

Пример 1. Найти минимальное остовное ордерево в графе, матрица весовых коэффициентов дуг которого имеет вид:

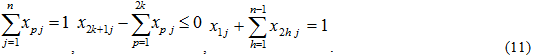
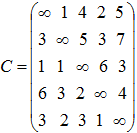
Решение. Матрица двоичных независимых переменных будет иметь вид , применение формулы (5) дает:

Подстановка в (6) приводит к целевой функции. Условия (11) запишутся в виде:

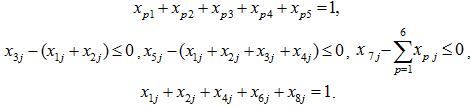
Для решения полученной задачи квадратичного программирования применим надстройку Solver (Поиск решения) программного комплекса Excel [3].

1. Вводим матрицу С в диапазон А1:Е5 (рис. 1), заменяя символ ∞ числом, которое значительно больше остальных чисел, например, числом 99:

 

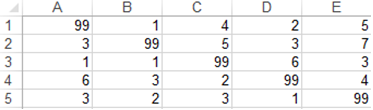
Рис. 1 – Входные данные

2. Под 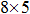 матрицу независимых двоичных переменных x_pj оставляем диапазон А7:Е14.
3. Матрицу 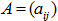 задаем в диапазоне А17:Е21 указанным ниже способом.

3.1. В ячейку В17 вводим формулу =$A$7*B8+$A$9*B10+$A$11*B12+$A$13*B14 и копируем ее в ячейки С17:Е17. 3.2. В ячейку А18 вводим формулу =$B$7*A8+$B$9*A10+$B$11*A12+$B$13*A14 и копируем ее в ячейки С18:Е18. 3.3. В ячейку А19 вводим формулу =$C$7*A8+$C$9*A10+$C$11*A12+$C$13*A14 и копируем ее в ячейки В19, D19:Е19. 3.4. В ячейку А20 вводим формулу =$D$7*A8+$D$9*A10+$D$11*A12+$D$13*A14 и копируем ее в ячейки В20:С20, Е20. 3.5. В ячейку А21 вводим формулу =$E$7*A8+$E$9*A10+$E$11*A12+$E$13*A14 и копируем ее в ячейки В21:D21.

4. В ячейку F7 вводим формулу =СУММ(A7:E7) и копируем ее в ячейки F8:F14 – они будут задавать первый блок ограничений (11).
5. В ячейку А15 вводим формулу =A7+A8+A10+A12+A14 и копируем ее в ячейки В15:Е15 – они будут задавать третий блок ограничений (11).
6. Задание формул блока 2 ограничений (11).

6.1. В ячейку H9 вводим формулу =A9-СУММ(A7:A8) и копируем ее в ячейки I9:L9. 6.2. В ячейку H11 вводим формулу =A11-СУММ(A7:A10) и копируем ее в ячейки I11:L11. 6.3. В ячейку H13 вводим формулу =A13-СУММ(A7:A12) и копируем ее в ячейки I13:L13.

7. Так как задача ни минимум, в изменяемые ячейки (диапазон А7:Е14) вставляем значение 1, что выполняется перед каждым применением надстройки «Поиск решения».
8. Вызываем надстройку «Поиск решения» и задаем (рис. 2) сценарий поиска решения:

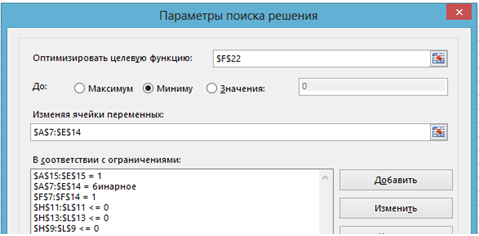
Рис. 2 – Сценарий поиска решения

      9. Команда «Найти решение» возвращает сообщение, что решение найдено и результаты (рис. 3).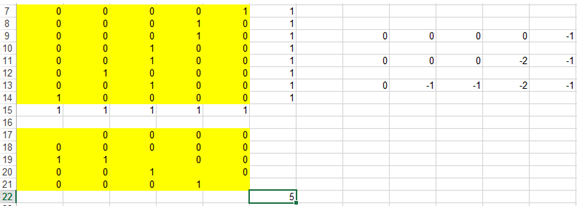  

Рис. 3 – Возвращаемые результаты

Как следует из данных диапазона А17:Е21, в минимальное остовное ордерево входят дуги (5, 4), (4, 3), (3, 1), (3, 2).

Теорема 2 применима и к симметричным матрицам.

Пример 2. Найти минимальное остовное дерево в графе, матрица весовых коэффициентов дуг которого имеет вид:

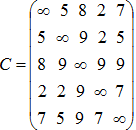
Решение. Заменяя на листе Excel с решением примера 1 данные диапазона А1:Е5 новыми данными и запуская поиск решения по сценарию, показанному на рисунке 2, получаем (рис. 4), что в минимальное остовное дерево входят дуги (1, 3), (2, 4), (2, 5), (4, 1).

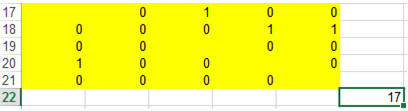
Рис. 4 – Возвращаемые результаты по данным примера 2

 

2. Некоторые частные случаи минимальных остовных ордеревьев

Из теоремы 2, с учетом условия (4), следует нахождение следующих частных случаев минимальных остовных ордеревьев.

1. Задача нахождения по матрице весовых коэффициентов С минимального остовного ордерева, корневой вершиной которого является заданная вершина с номером R, сводится к задаче квадратичного программирования (6, 11) при дополнительном ограничении .

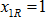Например, добавляя в сценарий решения (рис. 2) ограничение С7=1 и запуская поиск решения, получаем (рис. 5) матрицу смежности минимального остовного ордерева, корневой вершиной которого является вершина 3:

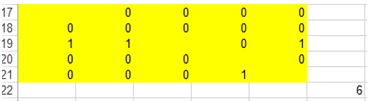
Рис. 5 – Корневая вершина имеет номер 3

В ордерево входят дуги (3, 1), (3, 2), (3, 5), (5, 4).

2. Задача нахождения по матрице весовых коэффициентов С минимального остовного ордерева, в котором висячей является вершина с заданным номером R, сводится к задаче квадратичного программирования (6, 11) при дополнительном ограничении .

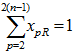Например, записывая в ячейке H15 листа Excel с решением примера 1 формулу =СУММ(C8:C14), добавляя в сценарий решения (рис. 2) ограничение H15=1 и запуская поиск решения, получаем (рис. 6) матрицу смежности минимального остовного ордерева, в которой вершина с номером 3 является висячей:

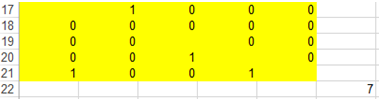
Рис. 6 – Вершина с номером 3 является висячей

 

Как следует из данных, показанных на рисунке 6, минимальное остовное ордерево образуют дуги (1, 2), (4, 3), (5, 1), (5, 4).

3. Задача нахождения по матрице весовых коэффициентов С минимального остовного ордерева, в котором транзитной является вершина с заданным номером R, сводится к задаче квадратичного программирования (6, 11) при дополнительных ограничениях .

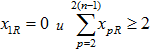В частности, записывая в ячейке J15 листа Excel с решением примера 1 формулу =СУММ(B8:B14), добавляя в сценарий решения (рис. 2) ограничения J15≥2, В7=0 и запуская поиск решения, получаем (рис. 7) матрицу смежности минимального остовного ордерева, в которой вершина с номером 2 является транзитной:

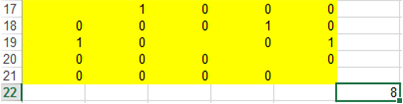
Рис. 7 – Вершина с номером 2 является транзитной

 

Входящие в ордерево дуги (1, 2), (2, 4), (3, 1), (3, 5).

Понятно, что рассмотренные случаи можно комбинировать.

4. Задача нахождения по матрице весовых коэффициентов С минимального остовного ордерева, корневой вершиной которого является заданная вершина с номером R, а висячей – вершина с номером S, сводится к задаче квадратичного программирования (6, 11) при дополнительных ограничениях .

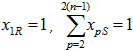Например, добавляя в сценарий решения (рис. 2) ограничения А7=1, H15=1 и запуская поиск решения, получаем (рис. 8) матрицу смежности минимального остовного ордерева, в котором вершина 1 является корневой вершиной, а вершина 3 – висячей:

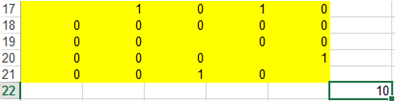
Рис. 8 – Вершина 1 является корневой, вершина 3 – висячей

 

Входящие в ордерево дуги (1, 2), (1, 4), (4, 5), (5, 3).

Заключение

Из приведенных результатов видно, что получены эффективные методы нахождения минимальных ориентированных остовных деревьев, включая нахождение многочисленных частных случаев этих деревьев.

Список литературы / References

1. Леонников А.В. Решение задач оптимизации в среде MS EXCEL / А.В. Леонников – М.: Издательский дом «Вильямс», 2005. – 704с.
2. Новиков Ф.А. Дискретная математика для программистов / Ф.А. Новиков – СПб: Питер, 2000. – 304 с.
3. Сдвижков О.А. Дискретная математика и математические методы экономики с применением VBA Excel / О.А. Сдвижков – М.: ДМК Пресс, 2012. – 212 с.
4. Филлипс Д., Гарсиа-Диас А. Методы анализа сетей: Пер. с англ. / Д. Филлипс, А. Гарсиа-Диас – М.: Мир, 1984.– 496 с.
5. Sdvizhkov O.A., Matsnev N.P. Problema generalizzato del albero ricoprente minimo / O.A. Sdvizhkov, N.P. Matsnev // Italian Science Review, 2016, 6 (39), P. 36-39

Список литературы на английском языке / References in English

1. Leonnikov A.V. Reshenie zadach optimizacii v srede MS EXCEL [The decision of tasks of optimization in environment MS EXCEL] / A.V. Leonnikov – M.: Publishing house "Williams", 2005. – 704 p. [in Russian]
2. Novikov F.A. Diskretnaja matematika dlja programmistov [Discrete mathematics for the programmers] / F.A. Novikov – SPb: Piter, 2000. – 304 p. [in Russian]
3. Sdvizhkov O.A. Diskretnaja matematika i matematicheskie metody jekonomiki s primeneniem VBA Excel [Discrete mathematics and mathematical methods of economy with application VBA Excel] / O.A. Sdvizhkov – M.: DMK Press, 2012. – 212 p. [in Russian]
4. Phillips D., Garcia-Diaz А. Metody analiza setej: Per. s angl. [Methods of the analysis of networks: Trans. from angl.] / D. Phillips, А. Garcia-Diaz – M.: Mir, 1984. – 496 p. [in Russian]
5. Sdvizhkov O.A., Matsnev N.P. Obobshhennaja zadacha o minimal'nom ostovnom derive [The generalized task about the minimal skeletal tree] / O.A. Sdvizhkov, N.P. Matsnev // Italian Science Review, 2016, 6 (39), P. 36-39