МЕТОДИКА ОЦЕНКИ ИНТЕНСИВНОСТИ СЕЛЬСКОХОЗЯЙСТВЕННОГО ПРОИЗВОДСТВА НА ОСНОВЕ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ

Стрюков М.Б.¹, Сахарова Л.В.¹, Алексейчик Т.В.², Богачев Т.В³.

¹Доктор физико-математических  наук, ²кандидат экономических  наук, ³кандидат физико-математических  наук, Ростовский государственный экономический университет (РИНХ)

МЕТОДИКА ОЦЕНКИ ИНТЕНСИВНОСТИ СЕЛЬСКОХОЗЯЙСТВЕННОГО ПРОИЗВОДСТВА НА ОСНОВЕ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ

Аннотация

Предложена модель расчета комплексной оценки уровня интенсификации сельскохозяйственного производства региона на основе теории нечетки множеств. В качестве критериев оценки использованы показатели двух групп: уровня интенсификации производства в сельском хозяйстве и уровня экономической эффективности интенсификации производства в сельском хозяйстве. Методика позволила получить оценку уровня интенсификации АПК в Ростовской области и дать рекомендации по его повышению.

Ключевые слова: теория нечетких множеств, лингвистическая переменная, комплексная оценка, уровень интенсификации производства.

Stryukov M.B.¹, Sakharova L.V.¹, Alekseichik T.V.², Bogachev Т.V.³

¹PhD in Physics and Mathematics, ²PhD in Economy, ³PhD in Physics and Mathematics, Rostov State University of Economy (RSUE)

METHODS FOR EVALUATION OF THE INTENSITY OF AGRICULTURAL PRODUCTION BASED ON THE THEORY OF FUZZY SETS

Abstract

The authors propose the model for calculating the integrated assessment of the intensification of agricultural production in the region based on the theory of fuzzy sets. The indicators of the two groups were used as the evaluation criteria: the level of intensification of agricultural production and the level of economic efficiency of the intensification of agricultural production. The method allowed to obtain the estimate of the level of intensification of the agro-industrial complex in the Rostov region and to give recommendations on its increase.

Keywords: theory of fuzzy sets, linguistic variable, complex estimation, level of production intensification.

Кафедра фундаментальной и прикладной математики Ростовского государственного университета (РИНХ)  на основе  расчетов  по показателям, предложенным Минсельхозпродом за 2014 – 2016 гг., предлагает оценку уровня интенсификации сельскохозяйственного производства Ростовской области с использованием теории нечетких множеств [1], [2] по критериям двух групп: уровень интенсификации производства в сельском хозяйстве и уровень экономической эффективности интенсификации производства в сельском хозяйстве.

Введем в рассмотрение лингвистические переменные: g= «комплексная оценка интенсификации производства в сельском хозяйстве Ростовской области»; g₁= «оценка уровня интенсификации производства в сельском хозяйстве Ростовской области»; g₂= «оценка экономической эффективности интенсификации производства в сельском хозяйстве Ростовской области».

Универсальным множеством для каждой лингвистической переменной является числовой отрезок [0,1], а множеством значений всех трех переменных g, g₁, g₂ – терм-множество , где G₁– «устойчивая тенденция  к уменьшению роста»; G₂– «тенденция к уменьшению роста»; G₃– «тенденция к стагнации»; G₄– «тенденция к росту»; G₅– «устойчивая тенденция к росту».

Введем лингвистическую переменную «Уровень показателя» с терм-множеством значений «Очень низкий, Низкий, Средний, Высокий, Очень Высокий». Для описания подмножеств этого терм-множества введем систему из пяти соответствующих функций принадлежности трапециедального вида:

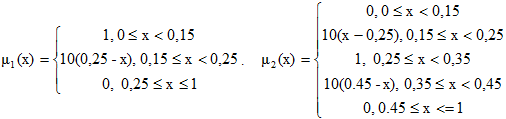
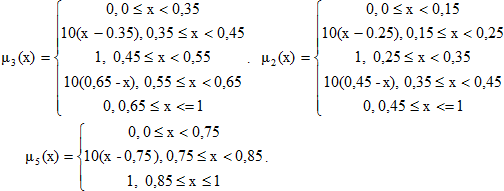
Везде в формулах  х – это [0,1]–носитель. Построенные функции принадлежности приведены на рис.1. Введем также набор так называемых узловых точек a_j = (0.1, 0.3, 0.5, 0.7, 0.9), которые являются, с одной стороны, абсциссами максимумов соответствующих функций принадлежности на [0,1]-носителе, а, с другой стороны,  равномерно отстоят друг от друга на [0,1]-носителе и симметричны относительно узла 0.5. Тогда введенную лингвистическую переменную «Уровень показателя», определенную на -носителе, в совокупности с набором узловых точек в теории нечетких множеств называют стандартным пятиуровневым нечетким [0,1]-классификатором.

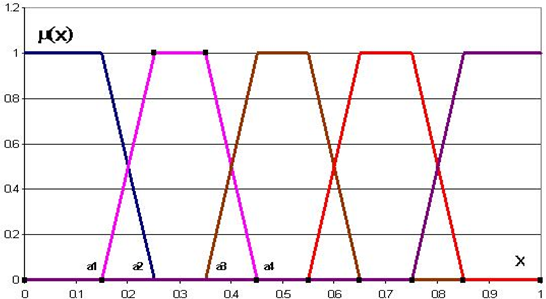
Рис.1 - Система трапециевидных функций принадлежности на -носителе

 

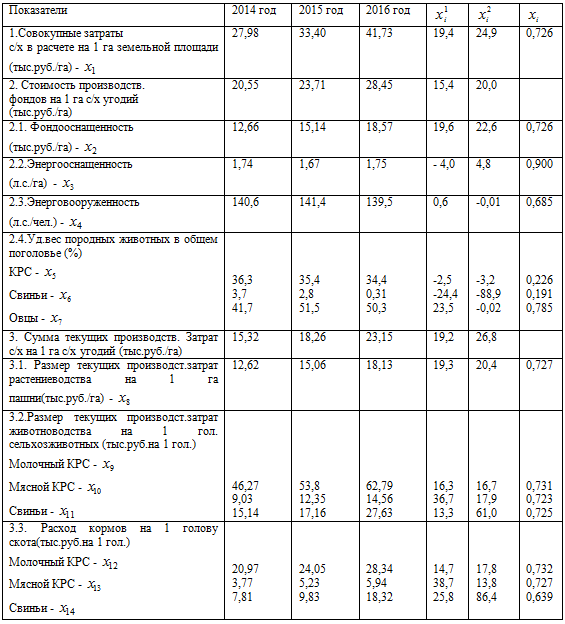
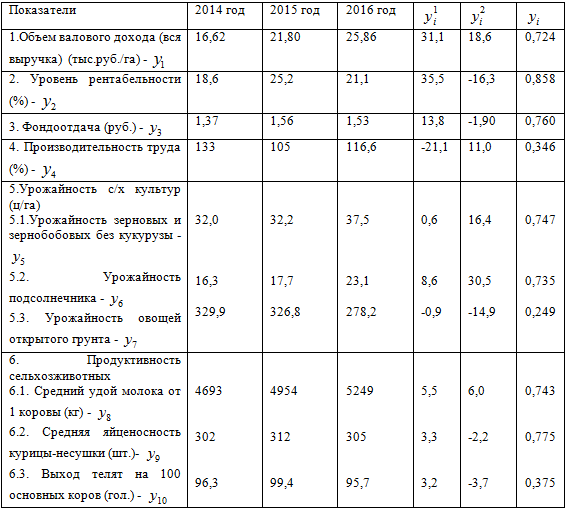
Оценку уровня интенсификации производства в сельском хозяйстве в Ростовской области будем производить по 14 показателям (табл. 1), а уровень экономической эффективности интенсификации производства в сельском хозяйстве в Ростовской области – по 10 показателям (таблица 2).

Введем обозначения для показателей первой группы (табл. 1):

 – темп прироста i – го показателя первой группы в 2015 году по отношению к 2014 году;  – темп прироста i – го показателя первой группы в 2016 году по отношению к 2015 году; x_i - числовое значение лингвистической переменной i – го показателя первой группы; соответственно, для показателей второй группы (табл. 2):

Таблица 1 – Показатели уровня интенсификации производства в сельском хозяйстве Ростовской области

 – темп прироста i-го показателя второй группы в 2015 году по отношению к 2014 году;  – темп прироста i-го показателя второй группы в 2016 году по отношению к 2015 году; y_i– числовое значение лингвистической переменной  i- го показателя второй группы.  

Таблица 2 –  Показатели экономической эффективности интенсификации производства в сельском хозяйстве Ростовской области

Числовые значения лингвистических переменных x_i, y_i предложено определять на основе следующей формулы:

   ( для y_i – аналогично),   (1)

где   – темп прироста показателя в 2016 году по отношению к 2014 году.

Схема вычисления числовых значений показателей этих лингвистических переменных представлена на рис.2.

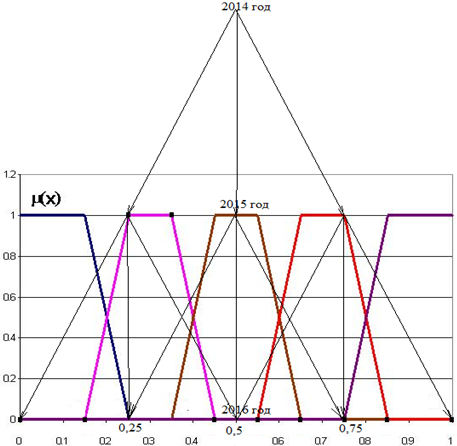
Рис. 2 – Схема вычисления числовых значений показателей этих лингвистических переменных

 

Каждая числовая переменная x_i, y_i является множеством-носителем лингвистических переменных B_i, C_i, состоящих из следующих термов: B_i1, C_i1 – «очень низкий уровень показателя»; B_i2, C_i2 – «низкий уровень показателя»; B_i3, C_i3 – «средний уровень показателя»; B_i4, C_i4 – «высокий уровень показателя»; B_i5, C_i5 – «очень высокий уровень показателя».

Показатели уровня интенсификации производства в сельском хозяйстве имеют различную значимость, поэтому предлагается ввести весовые коэффициенты для каждого показателя. Показатели уровня интенсификации производства образуют три группы: первая группа отражает совокупные затраты сельского хозяйства, вторая группа – стоимость производственных фондов, третья группа – текущие производственные затраты. При этом роль совокупных затрат и стоимости основных производственных фондов в оценке уровня интенсификации производства в сельском хозяйстве раскрывается через более подробные показатели: во второй группе – через показатели фондооснащенности, энергооснащенности, энерговооруженности и удельного веса породных животных в общем поголовье; в третьей группе – через показатели размера текущих производственных затрат растениеводства животноводства, расход кормов на 1 голову скота. В каждой группе показатели считаем равнозначными. Значения весов показателей представлены в табл. 3,4.

Правило перехода от значений показателей x_i к весам термов лингвистической переменной g₁ имеет вид:

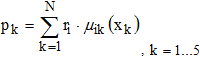  (2)

Тогда значение самой переменной g1  имеет вид    (3)

где -середины промежутков, являющихся носителями термов (рис.2),

g₁-«оценка уровня интенсификации производства в сельском хозяйстве Ростовской области». Для g₂  вычисления выполняются аналогично (табл. 4).

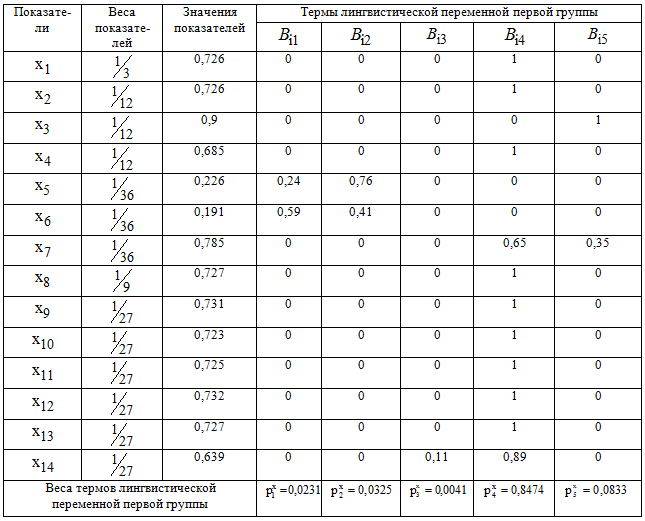
Таблица 3 – Веса и термы для показателей первой группы

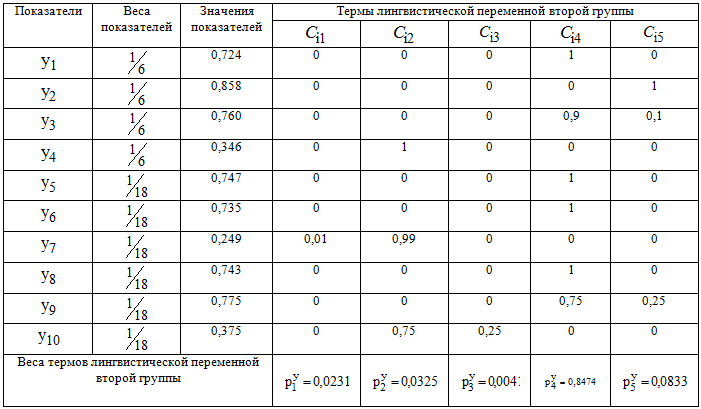
Таблица 4 – Веса и термы для показателей второй группы

Используя веса термов из таблиц 3 и 4, определенные на основании формулы (2), вычислим средние веса p_i для лингвистической переменной g:

Учитывая значения средних весов, а также  середины интервалов носителей термов (рис. 2),

на основании формулы  (3)  получим комплексную числовую оценку g интенсификации производства в сельском хозяйстве Ростовской области:

Следовательно, комплексная  оценка интенсификации производства в сельском хозяйстве Ростовской области в соответствии с введенным выше терм-множеством ,  соответствует терму G₄ – «тенденция к росту». Вычисляя по отдельности на основании формул (2) и (3), числовые оценки g₁= «оценка уровня интенсификации производства в сельском хозяйстве Ростовской области» и g₂= «оценка экономической эффективности интенсификации производства в сельском хозяйстве Ростовской области», получаем:

Следовательно,  «оценка уровня интенсификации производства в сельском хозяйстве Ростовской области» соответствует терму G₄– «тенденция к росту», а «оценка экономической эффективности интенсификации производства в сельском хозяйстве Ростовской области» – терму G₃– «тенденция к стагнации».

Таким образом, на основе построенной модели можно дать следующие рекомендации:

1. Необходимо обратить внимание на улучшение показателей экономической эффективности интенсификации производства в сельском хозяйстве.
2. Особое внимание уделить повышению урожайности овощей открытого грунта.
3. Провести необходимые мероприятия по повышению производительности труда.
4. Повысить процент выхода телят на 100 основных коров.

Список литературы / References

1. Nedosekin A.O. Fuzzy financial management / O.Nedosekin // Russia, Moscow, AFA Library, 2003. – 182 p.
2. Конышева Л.К. Основы теории нечетких множеств: Учебное пособие / Л.К.Конышева, Д.М.Назаров. – СПб.: Питер, 2011. – 192 с.

Список литературы на английском языке / References in English

1. Nedosekin A.O. Fuzzy financial management / A.O.Nedosekin // Russia, Moscow, AFA Library, 2003. – 182 p.
2. Konysheva L.K. Osnovy teorii nechetkih mnozhestv: Uchebnoe posobie [Fundamentals of the theory of fuzzy sets: a Training manual] / L.K.Konysheva, D.M.Nazarov. – SPb.: Piter, 2011. – 192 p. [in Russian]