ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ПАРАМЕТОРОВ И ГРАНИЦ РАЗВИТИЯ СИСТЕМЫ ЭНЕРГОПОТРЕБЛЕНИЯ

Мызникова М.Н.¹, Аксенов И.Б.², Газизуллин Р.М.³

¹ORCID: 0000-0002-6397-1475, кандидат экономических наук, доцент, Казанский (Приволжский) федеральный университет, ²ORCID: 0000-0001-7219-0761,  доктор  технических наук, профессор, Казанский национальный исследовательский университет (КАИ), ³ORCID:  0000-0003-3620-2467,  кандидат технических наук, доцент, Казанский государственный энергетический университет

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ПАРАМЕТОРОВ И ГРАНИЦ РАЗВИТИЯ СИСТЕМЫ ЭНЕРГОПОТРЕБЛЕНИЯ

Аннотация

В условиях открытых систем происходящие внутрисистемные и внешние изменения в распределении энергоресурсов имеют определенный характер. Оценка эффективности распределения энергоресурсов внутри системы представляет собой сложную научную задачу. Проявление фактора нарастающих внутрисистемных диспропорций во времени оказывают влияние на изменение качественного состояния системы и может существенно влиять на устойчивость системы и достижение целевых стратегических установок. Возможно определить состояние системы, ее качественное развитие и переход в новое состояние на основе применения новой парадигмы экономического развития – энтропии системы. В статье авторы предлагают на основе имитационного моделирования определить  параметры устойчивости системы энергопотребления. 

Ключевые слова: энергоресурс, гиперболическое распределение, энтропия.

Myznikova M.N.¹, Aksenov I.B.², Gazizullin R.M.³

¹ORCID: 0000-0002-6397-1475, PhD in Economy, Associate professor, Kazan (Volga region) Federal University, ²ORCID: 0000-0001-7219-0761, PhD in Engineering, Professor, Kazan National Research Technical University – KAI, ³ORCID: 0000-0003-3620-2467, PhD in Engineering, Associate professor, Kazan State Power Engineering University

IMITATIVE MODELING OF PARAMETERS AND BORDERS OF DEVELOPMENT OF THE ENERGY CONSUMPTION SYSTEM

Abstract

Under the conditions of open systems, the internal and external changes in the distribution of energy resources are of a certain nature. The evaluation of the efficiency of energy resources distribution within the system is a complex scientific problem. The manifestation of the factor of increasing the intra-system imbalances in time affects the change in the qualitative state of the system and can significantly affect the system stability and the achievement of targeted strategic attitudes. It is possible to determine the state of the system, its qualitative development and transition to a new state based on the application of a new paradigm of economic development - the entropy of the system. In this article the authors propose to determine the parameters of the stability of energy consumption system on the basis of simulation modeling.

Keywords: energy resource, hyperbolic distribution, entropy.

Баланс производства и потребления энергии в экономическом смысле представляет собой открытую систему. В условиях открытых систем объем потребляемых ресурсов, вследствие проводимой энергосберегающей политики, ценового давления и прочих рыночных ограничений, оказывает влияние на развитие экономических субъектов. В ходе проводимых реформ электроэнергетики проблема долгосрочного прогнозирования развития остается актуальной. Применяемые на современном этапе практические механизмы и методы регулирования позволяют прогнозировать возможность энергопотребления на среднесрочную перспективу, что явно недостаточно.

В зависимости от изменения показателя энергоэффективности предприятия могут менять «статус» по энергоемкости выпускаемой продукции, меняется и балансовая структура потребления. Внутри системы общее количество ресурсов может сохраниться, а может и нет (изменение  и  неопределенность спроса, развитие конкуренции  и т. д.).  Протекающие непрерывные процессы изменений в сложной системе энергопотребления характеризуются совокупностью  потребителей различных по масштабу и уровню экономического потенциала, что усложняет  задачи статистического оценивания развития  системы с использованием классических инструментов прогнозирования и ограничивает применение средних показателей в обосновании прогноза спроса.

Целью настоящего исследования является создание модели развития региональной системы энергопотребления на  основе имитационного моделирования. Объектом исследования является структура баланса потребления электроэнергии Республики Татарстан.

В основе модели лежит подход, сформулированный в  [4, С. 145-148] на основе выдвинутых теоретических положений Б. Мандельброта, позволивших  математически обосновать универсальность применения гиперболической зависимости в решении широкого спектра задач [3, С. 220–226]. Учитывая данное положение, оказалось возможным применение принципов имитационного моделирования в целях определения состояния параметров системы энергопотребления и  прогнозов развития.

Кластеризация и ранжирование энергопотребления региона по видам экономической деятельности (ОКВЭД) на основе среднестатистических показателей баланса электрической энергии  обнаруживает гиперболическую зависимость энергопотребления от числа хозяйствующих субъектов.   Предложенная модель определения функции интегрального энергоэкономического ценоза полезного потребления  позволила определить параметры гиперболической функции  и, на основе  предложенного критерия приращения энтропии, выделить системные ценностные потери ВРП [4, С. 145-148].

Результаты исследований показали, что за период с 2005- 2015 гг. произошло снижение  структурного параметра β от 0,2514 до 0,2325, показатель А практически не изменился и составил 10,53, отмечается рост ценностных потерь. Анализ полученных результатов позволил заключить, что прогнозирование потребления энергоресурса должно основываться на системных изменениях структуры потребления.

Имитационное моделирование осуществляется в несколько этапов.

1. Переход (с 2010 г.) промышленного производства с классификатора ОКП на ОКПД создал дополнительные проблемы при сопоставлении изменений электропотребления по отдельным направлениям добывающих и обрабатывающих производств. Замена классификатора сделала невозможным сравнение уровней использования среднегодовой производственной мощности организаций по выпуску отдельных видов продукции [1, С. 12]. В статистической базе информация по малым предприятиям только формируется. В долгосрочном периоде количество их может меняться. Таким образом, мы не знаем, каким будет системный коэффициент β, поэтому допускаем, что он меняется от минимального до максимального значения, определенного интегральным энергорэкономическим ценозом и внутриранговыми показателями β. Моделирование изменений и структурных сдвигов должно проводиться с учетом полученного прогноза распределения потоков энергии в системе.

Совокупность предприятий-потребителей электрической энергии, имеющих разный объем потребления, дохода и производства полезного продукта (полезность) моделируется гиперболическим распределением общего вида . В качестве аргумента распределения служит последовательность псевдослучайных чисел с числом отсчетов (предприятий) N=1000, которая ранжируется по убыванию. Число генераций в процессе стохастического моделирования принимается равным 30.

Сгенерированный таким образом случайный процесс удовлетворяет требованию стационарности, гистограмма распределения и автокорреляционная функция приведены на рис. 1, а, б.

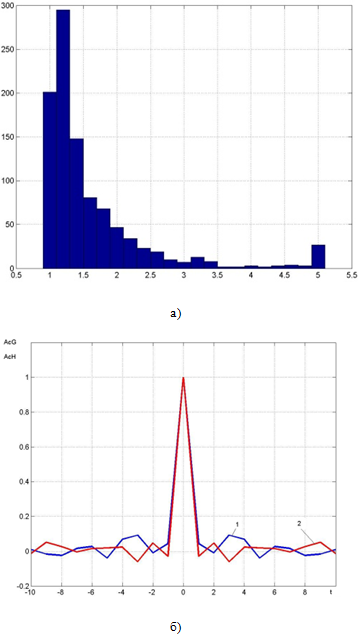
Рис. 1 – Гистограмма гиперболического распределения и автокорреляционная функция: а) гистограмма гиперболического распределения;  б) AcG – график автокорреляционной функции гауссова процесса (1);AcH - график  автокорреляционной функции гиперболической функции (2); t- время задержки

Можно заметить (см. рис. 1, б), что спад автокорреляционной функции практически такой же, как у случайного процесса.  В частном случае гиперболическое распределение практически совпадает с гауссовым распределением для абсолютных отклонений случайной величины, рассчитанных по соотношению [2, С.278]:

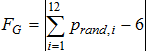   (1)

где  – равномерно распределенная случайная величина.

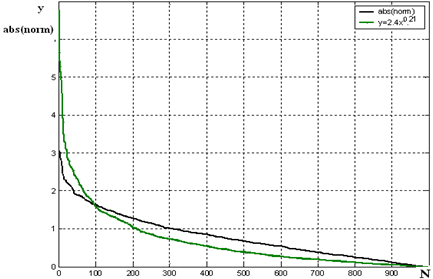
Численное моделирование показывает, что абсолютная величина Гауссова (нормального) распределения с единичной дисперсией соответствует степенному закону с параметрами , при этом среднеквадратичное отклонение не превышает величину  (рис. 2).

Рис. 2 – Аппроксимация абсолютного отклонения нормального распределения степенным законом   

3. Гиперболическое двухпараметрическое распределение вида 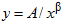 без потери общности позволяет множитель А принять равным единице. Результаты численного стохастического моделирования функции  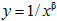на интервале значений  x  от  1 .... 1000  проиллюстрированы на графике  рис.3 (а) и в явном виде показывает смещение максимума  в зависимости от величины β.

Интеграл энтропийной функции гиперболического распределения (энтропия) коррелирует с величиной ВРП. Изменяя значение коэффициента , построим функции энтропийную функцию  (рис. 3).

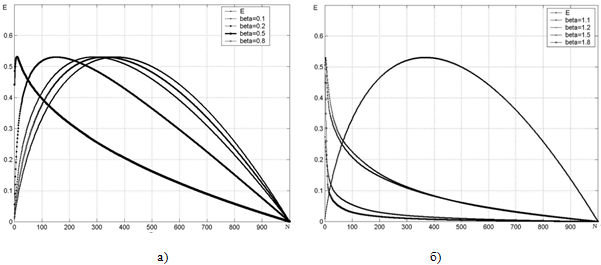
Рис. 3 – Графики энтропийной функции гиперболического распределения с показателем степени 

Представленные графики энтропийной функции гиперболического распределения при различных значениях β (см. рис. 3(а,б), приведенные значения показателя степени β гиперболического закона и соответствующие этому показателю значения энтропии H позволяют выявить существенную зависимость величины энтропии гиперболического распределения от показателя степени β. Параметры моделирования и значение энтропии представлены в табл. 1.

Таблица 1 – Зависимость энтропии от показателя степени

β	0,1	0,2	0,5	0,8	1,0	1,1	1,2	1,5	1,8
H	359,27…   360.18	354.71…   360.62	297.24 … 357.67	188.8 … 256.66	54.39…   184.63	7.886 … 137.77	14.0588 … 118.948	4.51 … 39.24	0.13…   13.48

 

Полученный результат для гиперболического распределения электропотребления позволяет констатировать наличие тенденции роста энтропии по мере уменьшения показателя β. В предельном случае, при β→0, соответствующем равномерному распределению вероятностей, энтропия достигает максимального значения. При этом снижается относительный разброс значений энтропии, который при β→2 достигает трех порядков, что объясняется фактором случайности генерации исходной равномерной последовательности, и, что естественно, в результате развития процессов самоорганизации энтропия растет.

Полученные результаты обладают практической значимостью в приложениях, связанных с задачами обоснованности прогноза энергопоребления. В условиях неопределенности, для устранения избыточности исходной информации влияющих факторов, независимо от их типа необходимо сначала проанализировать электропотребление.

Малое отклонение энтропии гиперболического распределения от максимального при значении показателя степени  позволяет варьировать  количество предприятий, сохраняя значение энтропии близким к максимальному. При этом средняя величина потребления уменьшается. Следовательно, на региональном уровне возникает возможность исследования результатов внедрения энергосберегающих проектов и программных мероприятий.

Уменьшение электропотребления следует из интеграла гиперболического распределения:

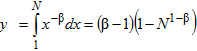   (2)

Значение интеграла при β→0  равно   и уменьшается с ростом коэффициента β, в частности при β=0.5 значение интеграла равно .

4. Имитационная модель гиперболического вида характеризуется различными значениями коэффициента β в зависимости от разбиения значений аргумента на кластеры. Варьирование интервалов разбиения на кластеры, соответствующих числу предприятий в кластере, при сохранении общего числа предприятий позволяет управлять величиной коэффициента β и решать задачу прогнозирования энергопотребления региона. Перераспределение границ кластеров достигается применением метода Нелдера-Мида  по критерию минимума разности величины энтропии между равномерным и гиперболическим распределением (см. рис.4).

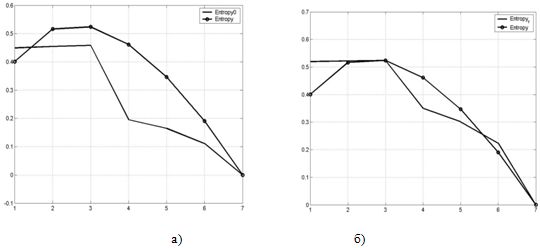
Рис. 4. Энтропийные функции полезного энергопотребления для параметров A=10,3889; β = 0,2514. за 2005 г.: а) энтропийные функции до оптимизации  б) энтропийные функции после оптимизации

Примечание: Entr0 – энтропийная функция для равновероятного распределения; Entr – функция приращения энтропии

Результаты апробации  предложенной модели представлены в табл. 2.

 

Таблица 2 – Изменение ранговой структуры потребления полезной энергии

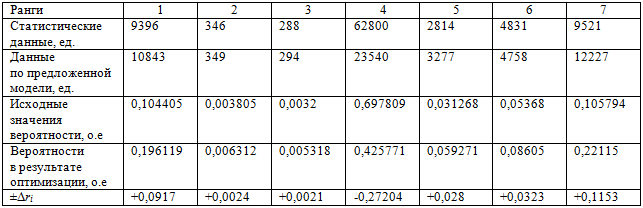
Примечание: относительная погрешность аппроксимации по данному критерию не превышает величину порядка 10^-4; ранговое распределение (про убыванию энергопотребления) за 2005 г.: 1– обрабатывающие производства; 2 – производство и распределение э/э, газа и воды; 3 – добыча полезных ископаемых ; 4 – др. виды эконом. деятельности; 5 – транспорт и связь; 6 – сельское хозяйство, охота и лесное хозяйство; 7 – строительство. Изменение значения структуры рангов ±Δr.

 

Из таблицы 2 видно, что следует развивать промышленность, строительные предприятия и организации. Интересным является факт «сокращения» организаций ранга «другие виды деятельности».  Прогнозирование электропотребления возможно осуществлять, изменяя показатель качественной характеристики функции полезной энергии β. Изменение объемов энергопотребления позволяет получить несколько вариантов эффективного использования энергии, максимизирующих системную полезность.

В заключении следует отметить, что исследуемая система регионального энергопотребления устойчива. Снижение энергопотребления,  как результат энергосберегающих мероприятий, не должно приводить к сокращению спроса. Необходимо повышать внутрисистемную энергоэффективность и развивать структуру потребления.

Список литературы / References

1. Антонов Н.В. Проблемы средне- и долгосрочного прогнозирования электропотребления в России / Н.В. Антонов // Материалы открытого семинара «Анализ и прогноз развития отраслей топливно-энергетического комплекса» (семинар А.С.Некрасова, 156 заседание от 24 февраля 2015 г.). – М.: Изд-во ИНП РАН, 2015. – 57 c. Режим доступа URL: http://ecfor.ru/wp-content/uploads/seminar/energo/zpdf
2. Кроновер Р.М. Фракталы и хаос в динамических системах. Основы теории / Р.М. Кроновер . – М.: Постмаркет, 2000. – 352 с.
3. Мандельброт Б.  Фракталы, случай и финансы / Б. Мандельброт. – Москва – Ижевск: Регулярная и хаотическая динамика, 2004. – 256 с.
4. Мызникова М.Н. Методика оценки эффективности энергопотребления региональной экономики / М.Н. Мызникова // Региональные проблемы преобразования экономики.- - №11.- С.  145-148.

Список литературы на английском языке / References in English

1. Antonov N.V. Problemy sredne- i dolgosrochnogo prognozirovanija jelektropotreblenija v Rossii [Problems of middle and long-term prognostication of electro-consumption in Russia] [Electronic resource] / N.V. Antonov // Materialy otkrytogo seminara «Analiz i prognoz razvitija otraslej toplivno-jenergeticheskogo kompleksa» (seminar A.S. Nekrasova, 156 zasedanie ot 24 fevralja 2015 g.) [Materials of open seminar "Analysis and prognosis of development of industries of fuel and energy complex" (seminar of A.S. Nekrasova, 156 meeting, 24 from February 2015 year)]. - M.: Izd-vo INP RAN, 2015. – 57 c. URL: http://ecfor.ru/wp-content/uploads/seminar/energo/z156.pdf (accessed: 10.12.2015) [in Russian].
2. Kronover R.M. Fraktaly i haos v dinamicheskih sistemah. Osnovy teorii / R.M. Kronover [Fractals and chaos in the dynamic systems. Bases of theory of] / R.M. Kronover . – M.: Postmarket, 2000. – 352 p. [in Russian]
3. Mandel'brot B. Fraktaly, sluchaj i finansy [Fractals, case and finansy] / B. Mandel'brot. – Moskva – Izhevsk: Reguljarnaja i haoticheskaja dinamika, 2004. – 256 р. [in Russian]
4. Myznikova M.N. Metodika ocenki jeffektivnosti jenergopotreblenija regional'noj jekonomiki [Method  of estimation of efficiency of energy consumption of regional economy] / M.N. Myznikova // Regional'nye problemy preobrazovanija jekonomiki [Regional economy conversion issues]. - 2015. - No. 11. – Р. 145-148. [in Russian]