ИСПОЛЬЗОВАНИЕ ИНТЕГРАЛЬНЫХ МЕТОДОВ В ЗАДАЧАХ МИГРАЦИИ ПОДЗЕМНЫХ ВОД

Карпенко Н.П.¹, Фуругян М.Г.²

¹ORCID: 0000-0001-6638-149Х, Доктор технических наук, Российский государственный аграрный университет РГАУ-МСХА имени К.А. Тимирязева, ²Кандидат физико-математических наук, ВЦ им. А.А. Дородницына ФИЦ «Информатика и управление» РАН

ИСПОЛЬЗОВАНИЕ ИНТЕГРАЛЬНЫХ МЕТОДОВ В ЗАДАЧАХ МИГРАЦИИ ПОДЗЕМНЫХ ВОД

Аннотация

В статье рассмотрено применение операционных математических методов для оценки миграционных параметров водоносных горизонтов при работе водозабора. Разработана методика оценки миграционных параметров водоносного пласта с использованием метода интегральных преобразований Лапласа (Лапласа-Карсона). По предложенной методике по данным режима эксплуатации конкретного водозабора определены основные миграционные параметры, которые могут использоваться при гидрохимических прогнозах на водозаборе.

Ключевые слова: водозабор, метод интегральных преобразований, миграционные параметры.

Karpenko N.P.¹, Furugyan M.G.²

¹ORCID: 0000-0001-6638-149Х, PhD in Engineering, Russian State Agrarian University-MSHA named after K.A. Timiriazev, ²PhD in Physics and Mathematics, VTS named after A.A. Dorodnicyn FIZ «Information and Management» of the RAS

USING INTEGRATED METHODS THE MIGRATION TASK GROUNDWATERS

Abstract

In the article application of operating mathematical methods is considered for the estimation of migratory parameters of aquiferous horizons during work of water intake. Methodology of estimation of migratory parameters of aquiferous layer is worked out with the use of method of integral transformations of Laplace (Лапласа-Карсона). On an offer methodology from data of the mode of exploitation of certain water intake basic migratory parameters that can be used for hydrochemical prognoses on a water intake are certain.

Keywords: water intake, method of integrated transformations, migration parameters.

Информационное обеспечение гидродинамических и гидрогеоэкологических прогнозов является одной из наиболее сложных и актуальных проблем в практике проектирования и эксплуатации водозаборов, гидротехнических сооружений, мелиоративных систем и т.д.  Повышение достоверности выполняемых прогнозов в задачах динамики и миграции подземных вод существенно зависит от  точности определения гидрогеологических и геомиграционных параметров [1, 2]. Основными современными методами решения поставленной проблемы являются применение таких операционных математических методов как метод интегральных преобразований Лапласа и Лапласа-Карсона, метод комбинаторных планов, методы регуляризации и т.д.  В качестве одного из методов решения задачи по определению параметров в задачах миграции был использован математический метод интегральных преобразований Лапласа (Лапласа-Карсона), применение которого сводится к вычислению несобственных интегралов, вычислению изображения опытной функции, методика которых рассмотрена в работе [3].

Использование математических методов проводилось на примере работы одного водозабора (Северный Таджикистан), подземные воды которого использовались на хозяйственно-питьевые нужды и для орошения [2]. Основной эксплуатируемый водоносный горизонт приурочен к песчаным отложениям четвертичного возраста. В процессе эксплуатации водозабора было установлено, что в водозаборных скважинах произошло увеличение минерализации выше критических значений (с 0,2 г/л до 4,2 г/л), что определило задачу прогноза качества воды в водозаборе путем решения эпигнозной задачи для определения геомиграционных параметров.

Изучение объекта исследований привело к целесообразности применения теоретической модели слоисто-блокового строения, включающей в себя три типа емкости: поровую – в проницаемых каналах, где перенос происходит по схеме поршневого вытеснения; блоковую – сосредоточенную в слабопроницаемых блоках, связанных с каналами условиями квазистационарного обмена; пластовую – в слабопроницаемых слоях, возможности насыщения которой могут считаться неограниченными [3, 4].

Уравнение солевого баланса в таком пласте будет иметь следующий вид:

     (1)

где:     – изменение количества солей в пористой емкости;   – изменение количества солей в блоковой емкости; χ – относительное содержание поровой емкости в породе; m – суммарная мощность проницаемых слоев в пласте; С и С* – концентрации солей в каналах и блоках; CV_z – перенос солей через кровлю и подошву пласта; V_z – сумма скоростей фильтрации через кровлю и подошву пласта;  – диффузионный поток в кровле, подошве пласта и по контакту с внутренними слабопроницаемыми слоями; ξ – число внутренних слоев;  – вертикальный градиент концентрации по контакту со слабопроницаемыми слоями;  – изменение количества солей по направлению потока в ленте тока шириной N и расходом Q; t – время.

Для связи между концентрациями солей в поровой и блоковой емкости служит уравнение внутреннего массообмена, которое имеет следующий вид [4]:

       (2)

где: a – коэффициент внутреннего массообмена.

При решении уравнений (1) и (2) наиболее целесообразно и удобно применить метод решения с помощью преобразования Лапласа-Карсона по временной переменной.  При этом переход от концентраций С и С* к их изображениям Ср и Ср* осуществляется  согласно общим правилам путем следующих замен:

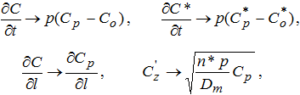    (3)

где:  р  – параметр преобразования. Тогда уравнение (1) и (2) преобразуются к виду:       (4)         (5)

Выражая Ср* из (5) и подставляя в (4), получим уравнение для изображения Ср:

       (6)

где:

 

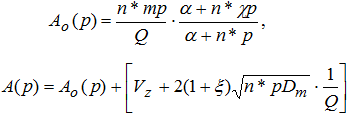
Таким образом, выражение (6) представляет собой дифференциальное уравнение первого порядка и в интервале от l = 0 до l = L имеет следующее общее решение вида для линейного в плане потока:

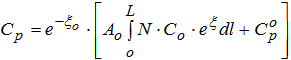    (7)

где: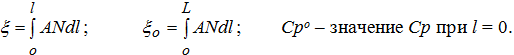 

При отсутствии начального засоления в потоке уравнение (7) имеет вид:

   (8)

В случае закачки раствора в скважину (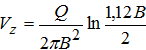, где B – параметр перетекания, Q – расход закачки) при отсутствии влияния проницаемости блоков на внутриблоковый обмен при N = 2πr уравнение (7) приобретает следующий вид:

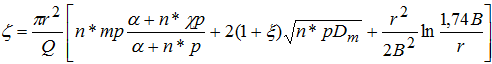   (9)

где: r – расстояние от центральной скважины до наблюдательной.

Определение миграционных параметров водоносного пласта сводится к представлению решения уравнения (9) в форме следующей зависимости:

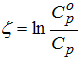   (10)

где: Ср^о и Ср – изображения концентраций раствора в центральной и наблюдательной скважинах.

Однако при закачке жидкости в пласт влияние пластовой емкости и перетекание через кровлю и подошву пласта незначительно и им можно пренебречь, тогда ζ(р) будет представлено в виде:

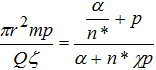     (11)

В случае, когда р < 1 (1/сут), т.е. при большой длительности налива в скважину величина n*χp становится весьма незначительной, расчеты можно вести с использованием следующей зависимости:

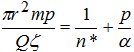    (12)

Как видно из выражения (12), основным параметром модели слоисто-блокового строения водоносного пласта является коэффициент эффективной пористости.  Для достоверной оценки этого параметра необходимо нахождение функции изображения от величин концентрации путем вычисления несобственных интегралов с использованием формулы:

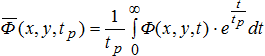   (13)

где:  – изображение функции Ф(х,у,t) по Лапласу-Карсону; t_р – параметр, вводимый для удобства и равный величине, обратной параметру преобразования р: t_р = 1/р.

Интегралы зависимости (13) удобнее вычислять путем метода механической квадратуры, согласно которому при определении численного значения по Лапласу-Карсону вычисляемая функция представляется в виде многочлена относительно аргумента t:

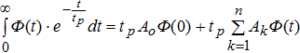    (14)

В первую очередь выбирается значение параметра t_р, и для заданной величины «n» находятся значения х_л и соответствующие им значения А_к.  Затем, при известных значениях t_р и х_к из соотношения t_к = х_к·t_р определяются моменты времени t_к, на которые по зависимости (14) снимаются известные значения функции концентрации Ф(t_к).  Для случая при «n» = 4 коэффициенты А_к определяются по таблице 1.

                Таблица 1 - Значения коэффициентов х_к и А_к

	0	1	2	3	4
хк	0	0,74321993	2,571635	5,7311788	10,953894
Ак	0,200	0,60120469	0,18573233	0,01294285	0,0001201262

  При подсчете суммы рядов достаточно ограничиться тремя-четырьмя первыми членами.  Использование метода механической квадратуры при выборе параметра t_р требует соблюдение и выполнение следующего условия: t_р  (0,06 – 0,1) Т.

Расчет параметров миграции эксплуатируемого водоносного пласта проводился для скважины, в которой отмечалось увеличение минерализации в некоторый период (Т = 730 сут).  В соответствии в приведенными выше зависимостями выбирались два параметра преобразования t_р = 73 сут (t_р = 1/6×Т) и t_р = 121 сут (t_р = 1/10×Т) и для них проводились расчеты концентрации С_р путем вычисления интеграла (7).  Результаты расчетов для водозаборной скважины приведены в таблице 2 для «n» = 4.

Таблица 2 - Результаты расчета величины изображения концентрации С_р при t_р = 73 сут и t_р = 121 сут.

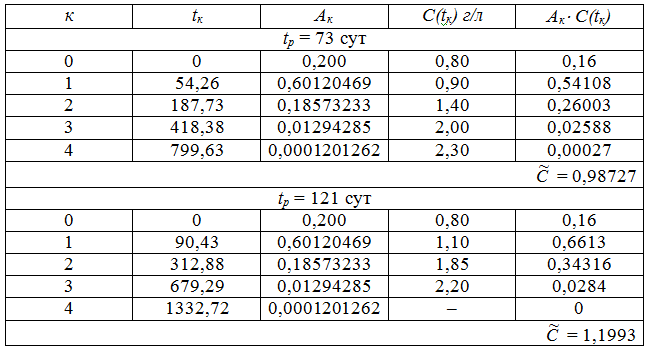
Далее, определив величины  = С_р, находим параметр ζ(р) с использованием зависимости (4):

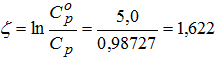
Далее, рассчитав р = 1/ t_р = 1/73 = 0,001369 и задаваясь величиной коэффициента солеобмена a, найдем величину эффективной пористости по зависимости:

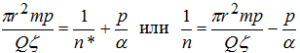
Таким образом, по данным роста минерализации подземных вод во времени в водозаборной скважине с использованием метода интегральных преобразований для схемы слоисто-блокового строения водоносного пласта был получен коэффициент эффективной пористости при различных значениях параметра р.  Решая совместную систему двух уравнений при двух различных значениях ζ и р, находим общую величину коэффициента эффективной пористости:

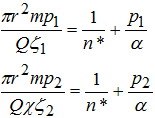       (15)

Решение системы уравнений (15) дало значение коэффициента эффективной пористости, равное n* = 0,139. Расчеты, проведенные по описанной выше методике для другой водозаборной скважины, находящейся в аналогичных гидрогеологических и гидрохимических условиях, показали довольно близкое значение коэффициента эффективной пористости n* = 0,140.

Таким образом, обработка данных режима эксплуатации водозаборных скважин с использованием интегральных методов показала применимость двух расчетных схем – схемы макродисперсии и схемы слоисто-блокового строения водоносной толщи изучаемого района.  Интерпретация данных режима эксплуатации и расчет полученных значений по схеме слоисто-блокового строения водоносной толщи в сравнении с результатами обработки опытных данных свидетельствует о хорошем совпадении величины эффективной пористости, которые могут быть достоверно использованы в расчетах прогнозной оценки качества воды в водозаборе.

Литература

1. Карпенко Н.П. Комплексная оценка емкостных и миграционных параметров водонасыщенных сред с использованием индикаторных методов // Международный научно-исследовательский журнал. – 2016. – №5-6(47). – С.82-84.
2. Карпенко Н.П., Манукьян Д.А., Питьева К.Е. Оценка гидрогеологических условий межгорных впадин для прогноза качества подземных вод при интенсивной их эксплуатации // Вестник МГУ, серия геологическая. – 1980. – № 6. – С. 89-96.
3. Манукьян Д.А. Теория и методы решения обратных задач геофильтрации: монография. – М.: МГУП. – 2007. – 188 с.
4. Шестаков В.М. Геогидродинамика: учебник. – М.: КДУ. – 2009. – 334 с.

References

1. Karpenko N.P. Kompleksnaja ocenka emkostnyh i migracionnyh parametrov vodonasyshhennyh sred s ispol'zovaniem indikatornyh metodov // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. – 2016. – №5-6(47). – S.82-84.
2. Karpenko N.P., Manuk'jan D.A., Pit'eva K.E. Ocenka gidrogeologicheskih uslovij mezhgornyh vpadin dlja prognoza kachestva podzemnyh vod pri intensivnoj ih jekspluatacii // Vestnik MGU, serija geologicheskaja. – 1980. – № 6. – S. 89-96.
3. Manuk'jan D.A. Teorija i metody reshenija obratnyh zadach geofil'tracii: monografija. – M.: MGUP. – 2007. – 188 s.
4. Shestakov V.M. Geogidrodinamika: uchebnik. – M.: KDU. – 2009. – 334 s.