GEOMETRIC AND STATISTICAL METHODS IN MODELING OF CONTACT INTERACTION OF BODIES
Юрьева Т.А.1, Филимонова А.П.2
1Кандидат педагогических наук, 2Кандидат физико-математических наук, доцент, Амурский государственный университет
ГЕОМЕТРИЧЕСКИЕ И СТАТИСТИЧЕСКИЕ МЕТОДЫ В МОДЕЛИРОВАНИИ ПРОЦЕССА КОНТАКТНОГО ВЗАИМОДЕЙСТВИЯ ТЕЛ
Аннотация
В статье исследуется возможность применения методов дифференциальной геометрии и вероятностно-статистических методов к моделированию технологического процесса контактного взаимодействия тел. В частности решается задача построения статистической оценки математического ожидания кривизны профиля тела, участвующего в контактном взаимодействии. При этом реальная поверхность моделируется регулярной поверхностью. Решение данной задачи находит применение в изучении процессов механической и физико-технической обработки, в технологии машиностроения.
Ключевые слова: кривизна кривой, кривизна поверхности, плотность вероятности, математическое ожидание.Yuryeva T.A.1, Filimonova A.P.2
1PhD in Pedagogy, 2PhD in Physics and Mathematics, assосiate professor, The Amur State University
GEOMETRIC AND STATISTICAL METHODS IN MODELING OF CONTACT INTERACTION OF BODIES
Abstract
The article explores the possibility of using methods of differential geometry and probabilistic and statistical methods to the modeling process of contact interaction of bodies. In particular, to solve the problem of constructing a statistical estimation of the expectation of the profile curvature of the body involved in contact. At the same time the real surface is simulated a regular surface. The solution to this problem finds application in the study of the processes of mechanical and physical-technical processing in mechanical engineering.
Keywords: the curvature of the curve, the curvature of the surface, the probability density, mathematical expectation.В настоящее время широкое распространение находит совместное применение методов геометрии и математической статистики. Например, язык дифференциальной геометрии используется для описания статистической модели и построения методов обработки данных. В данной работе рассматривается прикладная задача описания реальной поверхности с опорой на геометрию и математическую статистику.
Математическое моделирование реальной поверхности находит широкое применение в технике. В частности, при изучении зависимости различных физических характеристик от геометрии рельефа поверхности.
При построении математической модели исследователи применяют различные подходы к представлению о микрогеометрии поверхности: как о наборе выступов правильной геометрической формы; как о случайном поле; как о фрактальной структуре. В зависимости от выбранного подхода исследователи предлагают свои геометрические параметры, необходимые для моделирования рельефа поверхности.
Так, в исследовании Г.В. Литовки [1], изучавшем контактное взаимодействие тел и опирающемся на теоретико-вероятностный подход, в качестве такого параметра было введено понятие остроты L рельефа, которая определялась двумя независимыми друг от друга параметрами: кривизной профиля и количеством локальных максимумов профильной кривой на единице длины.
В данной работе мы упростили математическую модель, построенную автором, а именно, положили, что острота L определяется только кривизной k профиля кривой, так как гладкая плоская кривая и, как следствие, ее экстремумы полностью определяется своей функцией кривизны [2]. Задачей нашей работы явилось, с одной стороны, определение кривизны k профиля поверхности тела в целом и, с другой стороны, установление корреляции параметра L и кривизны профиля.
Будем считать, что поверхность F тела является замкнутой гомеоморфной сфере S2 и, по крайней мере, класса гладкости С2. Такую поверхность можно задать неявным уравнением F (x, y, z) = 0 в декартовых прямоугольных координатах или уравнением ρ=ρ (u, v) в сферических координатах, где центр системы координат помещён внутри тела. Принадлежность поверхности F классу гладкости С2 означает, что функция, задающая поверхность, является дважды дифференцируемой, то есть имеет непрерывные частные производные второго порядка. В каждой точке M регулярной поверхности F существует единственная касательная плоскость TмF. Обозначим через ![]() вектор нормали к TмF в точке M. Этот вектор для гладкой поверхности определён однозначно. Линии пересечения поверхности F плоскостями, проходящими через
вектор нормали к TмF в точке M. Этот вектор для гладкой поверхности определён однозначно. Линии пересечения поверхности F плоскостями, проходящими через ![]() , является нормальными сечениями поверхности F в точке М. Так как через точку M поверхности F можно провести пучок плоскостей, проходящих через
, является нормальными сечениями поверхности F в точке М. Так как через точку M поверхности F можно провести пучок плоскостей, проходящих через ![]() и провести аналогичные рассуждения относительно всех точек поверхности F, то получим множество профильных кривых одной поверхности F тела. Семейство профильных кривых одного тела можно рассматривать как выборку из генеральной совокупности профильных кривых, образованных всеми телами, участвующими в контактном взаимодействии. Далее считаем, что параметр K оценивает генеральную совокупность профильных кривых тел, участвующих в контактном взаимодействии. Таким образом, для параметра K имеем:
и провести аналогичные рассуждения относительно всех точек поверхности F, то получим множество профильных кривых одной поверхности F тела. Семейство профильных кривых одного тела можно рассматривать как выборку из генеральной совокупности профильных кривых, образованных всеми телами, участвующими в контактном взаимодействии. Далее считаем, что параметр K оценивает генеральную совокупность профильных кривых тел, участвующих в контактном взаимодействии. Таким образом, для параметра K имеем:
![]() (2)
(2)
Здесь N – количество тел, участвующих в контактном взаимодействии; Ki – среднее значение кривизны рельефа поверхности i-ого тела; N’ – совокупное множество профильных кривых, принадлежащих i-ому телу; Kij – кривизна рельефа j-ой профильной кривой i-ого тела. Пусть j-ая кривая i-ого тела является реализацией случайной функции ρj = ρj (θ)∈C2 заданной в полярных координатах.
Принимая за кривизну профиля в точке, кривизну соприкасающейся окружности в этой точке получаем E(K) = E![]() , где r – радиус соприкасающейся окружности к профильной кривой ρj = ρj (θ).
, где r – радиус соприкасающейся окружности к профильной кривой ρj = ρj (θ).
Величины математического ожидания кривизны профиля E![]() определяется по формуле:
определяется по формуле:
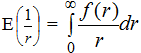 (3)
(3)
где f(r) – функция плотности вероятности радиусов кривизны в точках максимумов профильной кривой ρj = ρj (θ).
В свою очередь функция плотности вероятности радиусов кривизны задается выражением:
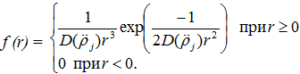 (4)
(4)
где D – дисперсия второй производной функции ρj = ρj (θ). После подстановки соотношение (4) в формулу (3), определим параметр E![]() в общем виде:
в общем виде:
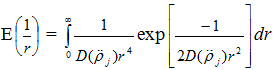 (5)
(5)
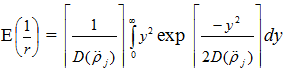 (6)
(6)
Воспользуемся табличным интегралом: ![]() , где p>0. Для нашего случая n=1, p=
, где p>0. Для нашего случая n=1, p=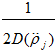 . Посредством выполнения несложных преобразований, выражение (6) примет вид:
. Посредством выполнения несложных преобразований, выражение (6) примет вид:
![]() (7)
(7)
В общем случае полученная функциональная зависимость (7) оценивает величину математического ожидания кривизны тел, участвующих в контактном взаимодействии.
Проанализируем формулу (7) для случая контактного взаимодействия моделируемого тела с плоским контртелом.
Рассмотрим случайную функцию ρj = ρj (θ). Примем кривую реализации этой функции, заключённую в интервале Δζ , за выборочную функцию ζ(ρ,θ) . Тогда значения выборочной функции ζ(ρ,θ) в интервале Δζ можно найти из следующего уравнения ![]() . Здесь E(R) – математическое ожидание радиуса кривизны средней линии профиля. Радиус кривизны средней линии профиля будет описываться функцией окружности кривизны R(r), где r – радиус соприкасающейся окружности к профильной кривой ρj. Последовательность случайных величин εj можно определить из годографа вектора , который описывает профильную кривую ρj = ρj (θ) тела, участвующего в контактном взаимодействии.
. Здесь E(R) – математическое ожидание радиуса кривизны средней линии профиля. Радиус кривизны средней линии профиля будет описываться функцией окружности кривизны R(r), где r – радиус соприкасающейся окружности к профильной кривой ρj. Последовательность случайных величин εj можно определить из годографа вектора , который описывает профильную кривую ρj = ρj (θ) тела, участвующего в контактном взаимодействии.
Известно, что дисперсия суммы случайных величин равна сумме их дисперсий. Тогда, дисперсия второй производной функции ρ = ρ (θ) может быть записана следующим образом:
![]() (8)
(8)
В случае контактного взаимодействия моделируемого тела с плоским контртелом, форма контактного участка моделируемого тела является практически шаровым сегментом. То есть функцию окружности кривизны R(r) можно рассматривать как постоянную величину: ![]() .
.
В силу проведенных рассуждений величина математического ожидания кривизны тел, участвующих в контактном взаимодействии запишется в следующем виде:
![]() (9)
(9)
В работе [1] последовательность значений εj описывается нормальной функцией с нулевым средним ![]() . Запись
. Запись ![]() приведена в декартовой системе координат. Случайной функции
приведена в декартовой системе координат. Случайной функции ![]() соответствует корреляционная функция
соответствует корреляционная функция ![]() , где
, где ![]() – среднее квадратическое отклонение ординат профиля описываемого годографом вектора
– среднее квадратическое отклонение ординат профиля описываемого годографом вектора ![]() , т.е. среднее квадратическое отклонение последовательности значений εj случайных ординат функции εj(x),
, т.е. среднее квадратическое отклонение последовательности значений εj случайных ординат функции εj(x),![]() – параметр, характеризующий чувствительность корреляционной связи между значениями случайных ординат εj функции
– параметр, характеризующий чувствительность корреляционной связи между значениями случайных ординат εj функции ![]() , τ – аргумент, отвечающий шагу корреляции.
, τ – аргумент, отвечающий шагу корреляции.
Воспользуемся аналогичными рассуждениями, для возможности сопоставления результатов. Известно, что ![]() – четвёртая производная функции
– четвёртая производная функции ![]() . Подставляя данное выражение в (9), получим:
. Подставляя данное выражение в (9), получим:
![]() (10)
(10)
Выражение (10) является расчётной формулой для математического ожидания кривизны профиля тела, участвующего в контактном взаимодействии.
Сравнивая, полученный результат, с введенным Литовкой Г.В., параметром – остротой L и его выражением через ![]() , заключаем, что параметр L и математическое ожидание кривизны профиля тела, участвующего в контактном взаимодействии E
, заключаем, что параметр L и математическое ожидание кривизны профиля тела, участвующего в контактном взаимодействии E![]() пропорциональны.
пропорциональны.
Таким образом, находит подтверждение наше предположение, о том, что острота L определяется только кривизной k профиля кривой.
Литература
- Литовка Г.В., Маничева Т.А., Филимонова А.П. О косвенной оценке режущих свойств абразивных гранул при виброабразивной обработке // Вестник Амурского государственного университета. Серия: Естественные и экономические науки. – 2002. – № 17. – С. 29-30.
- Филимонова А.П., Юрьева Т.А. Линеаризация как метод доказательства единственности решения для некоторого класса нелинейных дифференциальных уравнений на сфере // Вестник Амурского государственного университета. Серия: Естественные и экономические науки. – 2016. – № 73. – С. 25-28.
References
- Litovka G.V., Manicheva T.A., Filimonova A.P. O kosvennoj ocenke rezhushhih svojstv abrazivnyh granul pri vibroabrazivnoj obrabotke // Vestnik Amurskogo gosudarstvennogo universiteta. Serija: Estestvennye i jekonomicheskie nauki. – 2002. – № 17. – S. 29-30.
- Filimonova A.P., Yuryeva T.A. Linearizacija kak metod dokazatel'stva edinstvennosti reshenija dlja nekotorogo klassa nelinejnyh differencial'nyh uravnenij na sfere // Vestnik Amurskogo gosudarstvennogo universiteta. Serija: Estestvennye i jekonomicheskie nauki. – 2016. – № 73. – S. 25-28.
