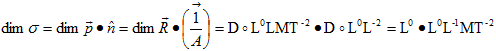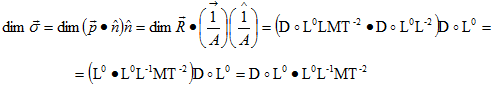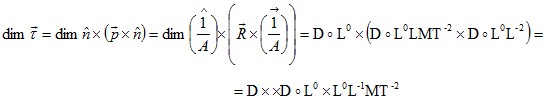О ВОЗМОЖНОСТИ СОЗДАНИЯ СИСТЕМЫ ВЕЛИЧИН МЕХАНИКИ, ЛИШЁННОЙ ОДНОИМЁННЫХ ВЕЛИЧИН (ЧАСТЬ III)

Терещенко В. Г.

Доцент, кандидат технических наук, Северо-Кавказский федеральный университет

О ВОЗМОЖНОСТИ СОЗДАНИЯ СИСТЕМЫ ВЕЛИЧИН МЕХАНИКИ, ЛИШЁННОЙ ОДНОИМЁННЫХ ВЕЛИЧИН (ЧАСТЬ III)

Аннотация

Проведены исследования в области теоретической метрологии, механики и геометрии. Цель – усовершенствование системы величин механики, достижение взаимного однозначного соответствия между размерностью и родом величины. Величина «угол» получила свою размерность. Найдёт применение в метрологии, образовании, компьютерных вычислениях.

Ключевые слова: метрология, система величин, размерность, механика, геометрия.

Tereshchenko V. G.

Associate professor, PhD in Engineering, North-Caucasus Federal University

ABOUT POSSIBILITY OF CREATION OF SYSTEM OF QUANTITIES OF THE MECHANICS DEPRIVED OF THE QUANTITIES OF THE SAME NAME (PART III)

Abstract

Researches in the field of theoretical metrology, mechanics and geometry are conducted. Goal – improvement of the system of mechanics quantities, the achievement of mutual-one correspondence between a dimension and a kind of quantity. The quantity of the "angle" got its own dimension. Will applications in metrology, education, computer calculations.

Keywords: metrology, system of quantities, dimension, mechanics, geometry.

Эта статья является продолжением статей [1] и [2]. В них излагается разработка новой системы величин механики, отличающейся наличием величины и размерности направления D, объединяемой в производную величину с величиной размерностного модуля L^αM^βT^γ при помощи величины нормированного модуля L⁰ и действия объединения «◦». В новой системе размерность вектора отличается от размерности скаляра, различные размерности имеют истинные векторы и псевдовекторы, скаляры первого и второго рода. Разные производные величины могут быть получены путём скалярного или векторного произведения векторов. Таким образом, многие величины механики, чьи размерности совпадают между собой в нынешней системе величин, соответствующей Международной системе единиц (СИ), получили в новой системе свои уникальные размерности. В [1] была поставлена цель – выявить возможность и пути создания такой системы величин механики, в которой одинаковой размерностью обладали бы только однородные величины. Можно ли говорить о том, что в [1] и [2] описание системы завершено, и поставленная в [1] цель достигнута полностью? Нет, в этих статьях не изложен способ представления размерности угла. Игнорирование величины «угол», которую считают безразмерностной, приводит к совпадению размерностей ряда самостоятельных величин механики. Поэтому в данной статье рассмотрим актуальную задачу, – разработать способ представления размерности угла. Следует также прояснить особенности образования размерностей при делении на направленную величину и формирования размерности суммы.

Рассмотрим представление величины «угол» в предлагаемой системе величин. Величина угла между двумя заданными направлениями, во-первых, показывает, насколько отличается одно направление от другого, во-вторых, показывает отношение длины дуги с центром в точке пересечения направлений, ограниченной этими направлениями, к её радиусу. В любом случае мы будем рассматривать угол как функцию двух заданных направлений. В предыдущих статьях [1, 2] были рассмотрены размерности величин, получаемых действиями с направлениями. Это размерности косинуса и синуса угла и величин, образованных с их помощью. Умножение длины заданного отрезка на косинус или синус угла возвращает величину проекции отрезка на заданное направление. Умножение же длины заданного отрезка на величину угла возвращает величину проекции отрезка на дугу, радиус которой равен проецируемому отрезку. Угол, как скалярная величина, играет роль коэффициента искажения при проецировании радиуса на дугу. Подобно умножению на синус угла между направлениями, при умножении на угол получаем новое направление, а не теряем одно измерение, как при умножении на косинус. Поэтому дуга получает направление. Приходим к необходимости ввести в рассмотрение величину «дуговой вектор». В отличие от криволинейной координаты дуговой вектор наделяем постоянным радиусом и собственным направлением в пространстве. Дуговому вектору соответствует единственный «прямой» вектор, соединяющий начало и конец дугового вектора. При таких условиях дуговые векторы можно складывать с прямыми векторами и между собой с получением единственного результата, выраженного суммарным прямым вектором. Дуговой вектор можно переносить параллельно самому себе в любую точку пространства, получая бесконечное множество равных дуговых векторов. Одинаковыми по своему действию оказываются и все дуговые векторы, соединяющие начало и конец одного прямого вектора. Для дугового вектора выбираем обозначение из набора имеющихся значков – дужка вниз.  – дуговой вектор A. Искомую математическую функцию двух направлений назовём «дуговым произведением».

Теперь рассмотрим размерности величин, полученных при помощи действия «дуговое произведение». Величины будем представлять по общей схеме [2], которая в общем случае содержит данные о направлении, нормированном модуле и размерностном модуле. В частных случаях некоторые позиции могут отсутствовать.

Для действия «дуговое произведение» выбираем значок  из таблицы символов или  из оператора формул. Действие «дуговое произведение» над направлениями  и  возвращает направление  от  в сторону  по дуге на плоскости, параллельной направлениям  и . Конкретизация по радиусу или длине дуги отсутствует. Но начальное направление дуги известно – направление касательной к дуге в начальной точке перпендикулярно направлению .

               (1)

где D◡D – размерность дугового направления. Т.е. размерность направления по дуге на плоскости, параллельной двум заданным направлениям, при заданном начальном направлении. На рисунке 1 показана дуга нормированного (единичного) радиуса.

Действие «дуговое произведение» над направлением  и единичным нормированным прямым вектором  возвращает единичную дугу , имеющую единичный радиус и единичную длину, направленную от направления  в сторону единичного прямого вектора Ê.

               (2)

где D◡D◦L⁰ – размерность единичной дуги, имеющей единичный радиус и единичную длину, направленной от заданного направления в сторону заданного единичного прямого вектора.

Действие «дуговое произведение» над единичными прямыми векторами  возвращает дугу, соединяющую концы единичных векторов  в заданной последовательности.

   (3)

где D◦L⁰◡D◦L⁰=D◡D◦L⁰◡L⁰ – размерность направленной дуги единичного радиуса, соединяющей концы двух единичных векторов. Т.е. размерность нормированного дугового вектора.

Если взять модуль от предыдущей величины с размерностью (3), получим  скалярную величину угла между направлениями.

    (4)

где L⁰◡L⁰ – размерность угла. Угол – это нормированный модуль дугового вектора.

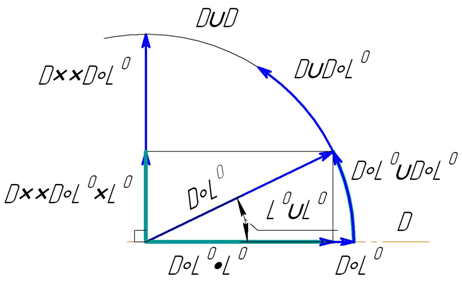
На рисунке 1 показаны нормированные геометрические величины и подписаны их размерности. В том числе показаны величины, полученные скалярным и двойным векторным произведением, рассмотренные в [1, 2].

Рис. 1 – Действия с единичным геометрическим вектором D◦L⁰ на плоскости и размерности полученных величин

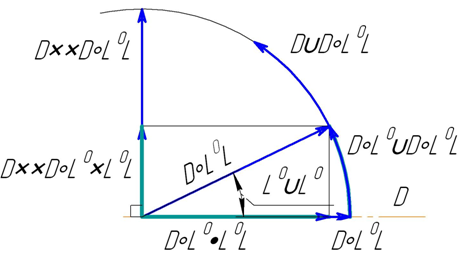
Такие величины и их размерности до сих пор не рассматривались в системах величин. Умножая полученные выше нормированные величины на какой-либо размерностный модуль, получим группу величин, которые в системе величин, соответствующей Международной системе размерностей, являются одноимёнными. Например, умножим каждую из этих величин на длину L и получим неединичные геометрические величины и их размерности, изображённые на рисунке 2. Все изображённые геометрические величины находятся в плоскости заданного направления с размерностью D и геометрического вектора с размерностью D◦L⁰L.

D◡D◦L⁰L – размерность дугового вектора с длиной, равной радиусу.

D◦L⁰◡D◦L⁰L – размерность дугового вектора с заданным радиусом между двумя заданными направлениями. Модуль этой величины

|D◦L⁰◡D◦ L⁰L|= L⁰◡L⁰L – размерность скалярной длины дуги.

Рис. 2 – Действия с геометрическим вектором на плоскости

Все величины на рисунке 2 – геометрические, это значит, что размерностный модуль представлен размерностью длины L или отсутствует. На рисунке 2 показаны также геометрические величины, полученные скалярным умножением и двойным векторным умножением. Обозначены их размерности, полученные в предыдущих частях статьи [1, 2].

Приведём один пример величины с размерностным модулем L².

D◦L⁰L◡D◦L⁰L= D◡D◦L⁰◡L⁰L² – размерность дугового вектора между двумя заданными направлениями, полный модуль которого с размерностью L⁰◡L⁰L² можно рассматривать как удвоенную площадь сектора или его проекции.

В общем случае размерность дугового вектора, как результата дугового произведения двух истинных прямых векторов

    (5)

где показатели степени α=α_B+α_E, β=β_B+β_E, γ=γ_B+γ_E получены сложением показателей степени при одинаковых основных величинах в размерностях сомножителей B и E.

Перейдём к пространственным величинам. Выполним дуговое произведение направлений перпендикуляров к плоскостям. Перпендикуляры получены путём векторного произведения направлений, принадлежащих плоскостям.

(D×D)◡(D×D) – размерность дугового направления поворота плоскости.

(D×D◦L⁰)◡(D×D◦L⁰) – размерность дуги поворота с единичным радиусом от перпендикуляра к одной паре направлений до перпендикуляра к другой паре направлений. Поворот в плоскости, параллельной обоим перпендикулярам. Иными словами – размерность нормированной дуги поворота плоскости. Модуль этой величины L⁰◡L⁰ можно рассматривать как угол поворота плоскости.

Рассмотрим особенности образования размерностей при делении на направленную величину. В известных системах величин производные величины получают не только путём перемножения основных и (или) производных величин, но и путём деления величин друг на друга. Т.е. показатель степени при основной величине в формуле размерности может быть положительным, равным нулю или отрицательным. В предлагаемой нами системе величин добавлены величина направления и действия скалярного и векторного произведения. Как известно, действие деления на вектор не предусмотрено, поэтому в уравнениях связи оно отсутствует. И в формулах размерности деление производится только на модуль величины. Возникает вопрос, нельзя ли точнее формализовать физический смысл величин, учитывая, что делитель может характеризоваться направлением в пространстве?

В предлагаемой нами системе величин вектор может иметь размерностный модуль с отрицательными значениями показателей степени основных размерностей. Т.е. деление на модуль может производиться независимо от действий с направлениями и нормированными модулями.

К тому же результату можно прийти, используя в уравнениях связи единичные векторы и отображая их размерности в формулах размерности.

Приведём пример определения размерностей полного, нормального и касательного механических напряжений. Пусть вектор силы  представляет сумму распределённых по площади A элементарных сил. Полное среднее напряжение  является вектором, а его размерность

    (6)

Проекция полного напряжения на нормаль к плоскости сечения имеет размерность

   (7)

Вектор нормального напряжения имеет размерность

    (8)

Вектор касательного напряжения имеет размерность

  (9)

Модуль касательного напряжения имеет размерность

  (10)

Скобки можно опустить. Здесь произведены сокращения, обусловленные повторным умножением на то же самое направление [2].

Как видим, все рассмотренные величины (6) – (10) имеют свои оригинальные размерности, т.к. у каждой из них есть свой оригинальный геометрический смысл. Базисом для всех геометрических построений служат направление нормали к плоскости сечения и вектор силы.

В новой системе величин свои особенности имеет соотношение размерностей слагаемых и суммы. Величины, в размерность которых входит размерность направления D, а размерностные модули совпадают, складываются и вычитаются между собой геометрически, а результат является вектором. Геометрически складываемые величины могут отличаться действиями (×,·,◡) между направлениями или нормированными модулями. См. рисунок 2 и формулы (6) – (10).

Отбросив в размерностях нормированные векторы, получим скаляры первого рода, выраженные только размерностными модулями. Скаляры первого рода можно складывать алгебраически, если их размерности совпадают. Результатом будет такой же скаляр первого рода. В частности, сложение величин с размерностью L даёт периметр геометрической фигуры или суммарную длину линий.

Отбросив в размерностях только направления с любыми действиями между ними, при наличии нормированных модулей у величин получаем полные модули истинных векторов, псевдовекторов и скаляры второго или третьего рода. Размерности слагаемых и суммы для них подчиняются теоремам геометрии, в частности, теореме Пифагора. Размерности σ, τ и p из примера связаны выражением

    (11)

   (12)

т.к. при действиях с одним и тем же углом между направлениями

   (13)

Векторные величины не складываются со скалярными.

Выводы.

Разработаны основные положения новой системы величин механики. В ней в полной мере учтены геометрические свойства величин. Добавлена размерность направления и нормированного единичного модуля, которые связаны между собой действием объединения. Для образования производных величин привлечены действия скалярного, векторного умножения и дуговое произведение, специально разработанное для создания размерности угла. Введена в рассмотрение величина «дуговой вектор», которая логически и математически связана с величинами угла и прямого вектора. Благодаря учёту геометрических свойств каждая механическая величина получает свою размерность, исчезают одноимённые величины, появляются размерности у величин, которые были безразмерностными или нераспознанными как самостоятельные величины.

Предлагаем обозначение для новой системы величин механики D◦LMT. Возможен сокращённый вариант обозначения DLMT. Поскольку механика является основой физики, система величин механики должна быть распространена на всю систему физических величин. Для доработки и признания или непризнания системы необходимы попытки практического применения системы многими специалистами. Поэтому мы предлагаем всем попрактиковаться в применении этой системы.

Литература

1. Терещенко В.Г. О возможности создания системы величин механики, лишённой одноимённых величин (Часть I) // http://research-journal.org/: Международный научно-исследовательский журнал. — 2015. URL: http://research-journal.org/wp-content/uploads/2011/10/5-2-36.pdf (дата обращения 16.06.2015).
2. Терещенко В.Г. О возможности создания системы величин механики, лишённой одноимённых величин (Часть II) // http://research-journal.org/: Международный научно-исследовательский журнал. — 2015. URL: http://research-journal.org/wp-content/uploads/2015/07/6-1-37.pdf (дата обращения 28.07.2015).

References

1. Tereshchenko V.G. O vozmozhnosti sozdanija sistemy velichin mehaniki, lishjonnoj odnoimjonnyh velichin (Chast' I) // http://research-journal.org/: Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. — 2015. URL: http://research-journal.org/wp-content/uploads/2011/10/5-2-36.pdf (data obrashhenija 16.06.2015).
2. Tereshchenko V.G. O vozmozhnosti sozdanija sistemy velichin mehaniki, lishjonnoj odnoimjonnyh velichin (Chast' II) // http://research-journal.org/: Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. — 2015. URL: http://research-journal.org/wp-content/uploads/2015/07/6-1-37.pdf (data obrashhenija 28.07.2015).