МОДЕЛИРОВАНИЕ ИНДУКЦИОННОГО НАГРЕВА ИЗОТЕРМИЧЕСКОГО КОНТЕЙНЕРА

Научная статья

Ларькина Т.С.

Выпуск: № 7 (38), 2015

Опубликована:

2015/08/15

PDF

Ларькина Т.С.

Аспирант, Филиал Национального исследовательского университета «МЭИ» в г. Смоленске

МОДЕЛИРОВАНИЕ ИНДУКЦИОННОГО НАГРЕВА ИЗОТЕРМИЧЕСКОГО КОНТЕЙНЕРА

Аннотация

В статье рассмотрено моделирование процесса индукционного нагрева изотермического контейнера. Приведены мероприятия по повышению равномерности прогрева сложной физически неоднородной среды.

Ключевые слова: индукционный нагрев, моделирование, равномерный прогрев, сельскохозяйственная продукция.

Larkina T.S.

Postgraduate student, The branch of the National Research University "MUE" in Smolensk

MODELING INDUCTION HEATING OF THE INSULATED CONTAINER

Abstract

The article considers the modeling of induction heating of the insulated container. There are measures to improve the uniformity of the heating of the complex physically inhomogeneous medium.

Keywords: induction heating, modeling, uniform heating, agricultural products.

Высокая популярность индукционного нагрева обоснована возможностью регулирования пространственного расположения зоны протекания вихревых токов, а, следовательно, и нагрева; высокоскоростной разогрев любого электропроводящего материала; возможность передачи электрической энергии непосредственно в нагреваемое тело, которая позволяет осуществить прямой нагрев проводниковых материалов; надежность, долговечность; обеспечивает высокие КПД и cos φ на промышленной частоте тока 50 Гц [1, 2].

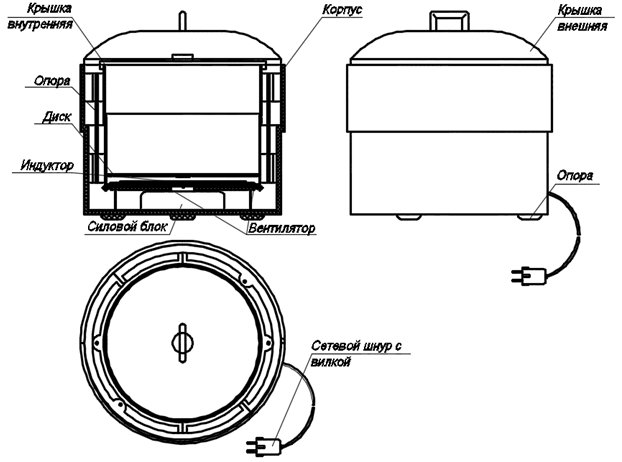
Один из возможных вариантов конструктивного исполнения установки для термической обработки продуктов питания приведен на рисунке 1 [3].

Рис. 1 – Модуль тепловой обработки

Так как рассматриваемая система сложная и охватывает собой процесс теплообмена между жидкостью (водой) и твердыми телами при их непосредственном соприкосновении. Нагрев жидкости в изотермическом контейнере происходит за счёт джоулева тепла, выделяющегося под действием индуцированных в стенках и днище изотермического контейнера токов. Следовательно, этот процесс осуществляется одновременным действием теплопроводности и конвекции с распределенными объемными параметрами.

Тепловое состояние отдельных частей тела в процессе теплопроводности различно, то в общем случае температура является функцией координат x, y, z и времени τ, то есть [4]:

t=f(x,y,z,τ) (1)

Явление теплопроводности в жидкостях и в твердых телах вполне может определяться градиентом температуры и коэффициентом теплопроводности. Иначе обстоит дела с явлением конвекции. Перенос тепла здесь неразрывно связан с переносом жидкости.

В нашем случае количество переданного тепла является функцией формы Φ, размеров l_x,l_y,l_z, температуры τ_i, материала и поверхности нагрева изотермического контейнера и содержимого этого контейнера, а именно: физических параметров нагреваемых объектов – коэффициентов теплопроводности λ_i, теплоемкости c_i, плотности ρ_i стеклянных банок, металлических крышек для закупоривания и содержимого стеклянных банок, а также скорости жидкости ϖ, ее температуры τ, физических параметров жидкости (воды) – коэффициента теплопроводности λ, теплоемкости c, плотности ρ, вязкости μ. Таким образом [5],

Q=f(Φ l_x,l_y,l_z,τ_i,ϖ,τ,λ,c,ρ,μ,λ_i,c_i,ρ_i) (2)

Сложная физически неоднородная структура нагреваемой системы, а также неравномерное распределение скорости потока по объему не позволяют использовать для решения тепловой задач аналитические методы расчета, поэтому в данной принимаем следующие допущения:

ограничиваемся двухмерным пространством;
при изучении нестационарных тепловых процессов пренебречь влиянием переходных режимов электромагнитного поля ввиду малой инерционности электромагнитных процессов в сравнение с тепловыми;
рассматриваем более упрощенную систему относительно содержимого установки, т.е. такой вариант, когда во внутреннем контейнере расположена стеклянная емкость формой, повторяющей внутренний контейнер установки. Данная стеклянная емкость заполнена однородной средой – водой;
индуктор выполнен в форме спирали Архимеда;
частоту принимаем равной f=5000 Гц.

С учетом принятых допущений имеет место раздельное решение электромагнитной и тепловой задач.

Произведем моделирование в среде ELCUT 5.1 Professional. На рисунке 2 приведено в разрезе распределение вихревых токов на дне контейнера при нагреве установки для термической обработки продуктов питания.

Рис. 2 – Распределение вихревых токов (увеличено и включена сетка конечных элементов)

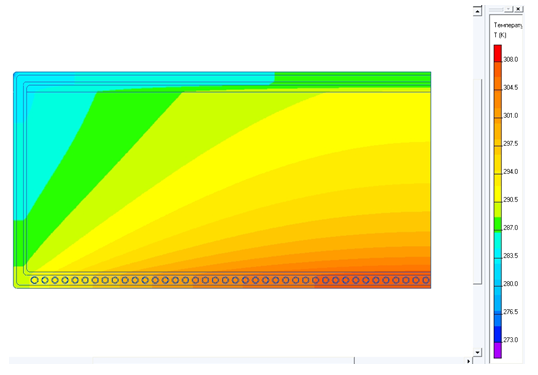
Для тепловой задачи задаются конвективные условия теплообмена на внешних границах и условия сопряжения двух сред на внутренней границе. Результаты моделирования тепловой задачи приведены на рисунке 3.

Рис. 3 – Распределение тепла в контейнере

Как видно на рисунке 3, в данной системе за единицу времени имеет место неравномерный прогрев.

Этот вопрос становится особенно острым, когда объем изотермического контейнера будет заполнен не однородной средой (водой), а иными твердыми телами (сельскохозяйственной продукцией), обладающими более высокой вязкостью, которые необходимо нагревать до определенной температуры и поддерживать ее в течение определенного периода времени. С целью повышения эффективности нагрева можно применить несколько способов:

барботирование,
применение различных конструктивных вариаций изотермического контейнера (например, вариант исполнения дна изотермического контейнера со впадинами, в которые будут помещены два индуктирующих провода, токи в которых равны и направлены одинаково),
вариант монтажа ферромагнитного стержня по центру внутри изотермического контейнера,
применение иных ферромагнитных емкостей внутри контейнера.

Литература

Ларькина Т.С. Исследование процесса нагрева изометрического контейнера индукционным нагревом/ Т.С. Ларькинаа; Науч. рук. канд. техн. наук, доц. Г.С. Леневский// Информационные технологии, энергетика и экономика. XI международная научно-техническая конференция. Сборник трудов. 17-18 апреля 2014, г. Смоленск - Смоленск: ФГБОУ ВПО "НИУ МЭИ" в г. Смоленске, 2014.
Розанов Ю.К. Полупроводниковые преобразователи со звеньями повышенной частоты / Ю.К. Розанов. – М.: Энергоатомиздат, 1987. – 184 с.: ил.
Ларькина Т.С. К вопросу формирования общей конструкции системы индукционного нагрева / Т.С. Ларькина; Науч. рук. канд. техн. наук, доц. Г.С. Леневский // Новые горизонты: материалы международной конференции-конкурса, Брянск, 19 марта 2014 г./ [Текст] + [Электронный ресурс]/под ред. О.М. Голембиовской. - Брянск: БГТУ, 2014. – С. 13-14.
Михеев М.А., Михеева И.М. Основы теплопередачи. // М.: Энергия. 1977. С. 344 с ил.
Слухоцкий А.Е., Рыскин С.Е. Установки для индукционного нагрева. // Л.: Энергоиздат, 1981. С. 326 с ил.

References

Lar'kina T.S. Issledovanie processa nagreva izometricheskogo kontejnera indukcionnym nagrevom/ T.S. Lar'kinaa; Nauch. ruk. kand. tehn. nauk, doc. G.S. Lenevskij// Informacionnye tehnologii, jenergetika i jekonomika. XI mezhdunarodnaja nauchno-tehnicheskaja konferencija. Sbornik trudov. 17-18 aprelja 2014, g. Smolensk - Smolensk: FGBOU VPO "NIU MJeI" v g. Smolenske, 2014.
Rozanov Ju.K. Poluprovodnikovye preobrazovateli so zven'jami povyshennoj chastoty / Ju.K. Rozanov. – M.: Jenergoatomizdat, 1987. – 184 s.: il.
Lar'kina T.S. K voprosu formirovanija obshhej konstrukcii sistemy indukcionnogo nagreva / T.S. Lar'kina; Nauch. ruk. kand. tehn. nauk, doc. G.S. Lenevskij // Novye gorizonty: materialy mezhdunarodnoj konferencii-konkursa, Brjansk, 19 marta 2014 g./ [Tekst] + [Jelektronnyj resurs]/pod red. O.M. Golembiovskoj. - Brjansk: BGTU, 2014. – S. 13-14.
Miheev M.A., Miheeva I.M. Osnovy teploperedachi. // M.: Jenergija. 1977. S. 344 s il.
Sluhockij A.E., Ryskin S.E. Ustanovki dlja indukcionnogo nagreva. // L.: Jenergoizdat, 1981. S. 326 s il.