ГРАДУИРОВАНИЕ И КОРРЕКТИРОВКА ДАТЧИКА ТЕМПЕРАТУРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО ИСПОЛЬЗОВАНИЯ (БЕЗ ТЕРМОПАРЫ) ПРИ ПОМОЩИ НЕЛИНЕЙНОГО ДИНАМИЧЕСКОГО МОДЕЛИРОВАНИЯ

Г.Н. Лукьянов¹,  С.А. Полищук², И.С.Ковальский³

¹Доктор технических наук, ²Аспирант, ³Аспирант, Университет ИТМО

ГРАДУИРОВАНИЕ И КОРРЕКТИРОВКА ДАТЧИКА ТЕМПЕРАТУРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО ИСПОЛЬЗОВАНИЯ (БЕЗ ТЕРМОПАРЫ) ПРИ ПОМОЩИ НЕЛИНЕЙНОГО ДИНАМИЧЕСКОГО МОДЕЛИРОВАНИЯ

Аннотация

Представлена апробация метода градуирования и корректировки датчика температуры, при помощи нелинейного динамического моделирования на основе алгоритма метода или модели NARMAX (Non-Linear Auto-Regressive Moving Average with Exogeneous Inputs, то есть нелинейной авторегрессивной модели скользящего среднего значения с внешними входами). Датчик построен на основе термистора и термопары. Градуирование и корректировка датчика необходимо для его самостоятельного использования без термопары.

Ключевые слова: нелинейное динамическое моделирование, NARMAX, датчик, термистор, термопара, результаты температурных измерений, синхронизация.

N. Lukyanov¹, S. A. Polistshouk², I. S. Kowalski³

¹doctor of technical Sciences, ²post graduate student, ³postgraduate student, University ITMO

CALIBRATION AND ADJUSTMENT OF TEMPERATURE SENSOR FOR INDEPENDENT USE (WITHOUT THERMOCOUPLE) USING NONLINEAR DYNAMIC MODELING

Abstract

The method has been evaluated calibration and adjustment of temperature sensor using nonlinear dynamic simulation based on the algorithm of the method or model NARMAX (Non-Linear Auto-Regressive Moving Average with Exogeneous Inputs, i.e. nonlinear autoregressive models moving average with external inputs). The sensor is based on the thermistor and thermocouple. Calibration and adjustment of the sensor is necessary for its independent use without thermocouple.

Keywords: nonlinear dynamic modeling, NARMAX, sensor, thermistor, thermocouple, temperature measurements, synchronization.

Известно, что процессы, протекающие в природе, в большинстве случаях являются периодическими, нелинейными и динамическими. К таким процессам относятся нестационарные процессы теплообмена, в частности теплообмен при кипячении воды. Для проведения и мониторинга температурных измерений создаются разнообразные датчики температуры на основе термопар и термисторов. При проведении температурных измерений новыми датчиками возникают вопросы, связанные с их корректировкой и градуированием. Для этого существуют несколько способов, таких как использование эталонных процессов, где заранее известно поведение процесса и статистические методы. Одним из таких методов является нелинейное динамическое моделирование.

Для построения динамических моделей можно применять, например, метод ARMAX (Auto-Regressive Moving Average with Exogeneous Inputs), реализованный в пакете MATLAB. Однако процедура ARMAX строит только линейные модели и ее целевая функция линейна по управляющим переменным. Для устранения этих недостатков разработана нелинейная модель на основе метода NARMAX (Non-Linear Auto-Regressive Moving Average with Exogeneous Inputs) [1,2,3], которая обладает следующими достоинствами:

1. модели NARMAX подходят для описания обширной области нелинейного динамического поведения процессов;
2. модели NARMAX удобны для описания реальных процессов

Целью настоящей работы является апробация применения модели NARMAX для апробации метода градуирования и корректировки датчика температуры, при помощи нелинейного динамического моделирования. Для этого нужно решить задачу нелинейного динамического моделирования на основе экспериментально зарегистрированных рядов наблюдений информационных процессов. Информацией для построения нелинейной динамической модели NARMAX служат результаты синхронных измерений колебаний температуры при кипячении воды.

В работе впервые продемонстрировано применение метода NARMAX для корректировки и градуирования датчика температуры.

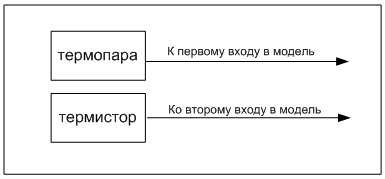
В работе проведено исследование модели, с двумя входами (сигналы от термопары и термистора). В экспериментах использовался прибор датчик температуры, схема которого показана на рисунке 1. Датчик разработанный на кафедре Сенсорики Университета ИТМО. Этот датчик содержит термопару, имеющую высокую инерцию к изменению температуры, и термистор, имеющий низкую инерцию к изменению температуры. Данное исследование необходимо для самостоятельного использования датчика без термопары. Это обусловлено снижением стоимости производства датчика.

Рис. 1 - Схема датчика температуры

Вышесказанное говорит о научной новизне этой работы

Описание и решение проблемы

Использована нелинейная авторегрессивная модель скользящего математического ожидания с внешними входами по методу NARMAX [2]. Математически она представляет собой полиномиальное выражение, состоящее из последовательности многочленов. Численные коэффициенты элементов многочленов данной последовательности являются элементами матрицы коэффициентов, встраиваемую в модель по окончании итерационного процесса построения модели. Указанный процесс проиллюстрирован на рисунке 2 далее на примере сопоставления результатов температурных измерений при дыхании человека и расчета по модели.

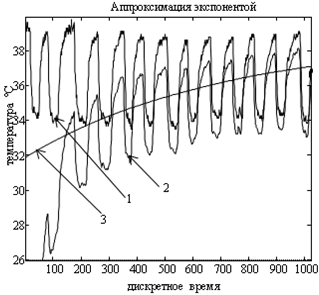
Рис. 2 - Реакция модели на процесс: 1 – значения температуры вдыхаемого–выдыхаемого воздуха на входе в ноздри, 2 – модель на этапе подстройки под процесс дыхания

На этом рисунке также показан принцип действия метода NARMAX для построения нелинейных динамических моделей. Из имеющегося набора данных одновременно анализируются от 100 до 1000 отсчетов, составляющих апертуру ("окно") метода. Размер "окна" установлен экспериментально. Модель (рис. 2, кривая 2) ведет себя как реальный физический прибор, подстраиваясь под описываемый процесс (кривая 1) по экспоненте (кривая 3). По окончании очередной итерации метод NARMAX выводит результат моделирования, после чего смещает "окно" на один отсчет и проводит очередную итерацию. Также модель может быть использована в качестве цифрового фильтра, который может очищать входной сигнал от нежелательных помех и ненужных для исследования частот. В настоящее время разрабатывается математический аппарат для адаптивной настройки этого фильтра.

Аналитически принцип действия метода NARMAX можно представить на примере работы с полиномиальными выражениями, состоящими из последовательностей многочленов, которые являются математическим представлением моделей синхронизации электрического сигналов, идущих от термопары и термистора. Метод NARMAX, используя процедуру ортогонализации, позволяет произвольно менять степень этих многочленов. Эта особенность данного метода использована для фиксирования всех экстремумов исследуемых процессов, т. е. повышения чувствительности модели. При этом на каждой итерации не только подбираются степени многочленов, но и проверяется значимость вклада его членов в модель. Незначимые члены метод NARMAX отбрасывает – их коэффициенты приравниваются нулю. В ходе многочисленных экспериментов по применению метода NARMAX для построения моделей, что процедура ортогонализации выбирает степень многочлена на основе соотношения дисперсий процессов и их моделей [3].

Модель сигнала, идущего от термопары:

          (1),

Где (a₀, a₁, …, a_n) – это столбцы матрицы коэффициентов модели сигнала, идущего от термопары, t – дискретное время, τ – временная задержка, в данном случае равная нулю,

модель сигнала, идущего от термистора:

          (2),

где (b₀, b₁, …, b_n) – это столбцы матрицы коэффициентов модели сигнала, идущего от термистора

Общая модель сигналов идущих от термистора и термопары:

          (3)

Модель ведет себя как реальный физический прибор, подстраиваясь под описываемый процесс по экспоненте, что показано на рис. 2. Это было выявлено в ходе проведенного исследования возможностей данной модели. Также модель может быть использована в качестве цифрового фильтра, который может очищать входной сигнал от нежелательных помех и ненужных для исследования частот.

Если рассматривать потоки данных, которые подаются на входы в модель как совокупность векторов равной длины, то данные векторы можно объединить в одну матрицу, которая удобно может быть представлена в виде таблицы данных. Использование такой таблицы данных существенно сокращает время на построение модели с несколькими входами.

На рис. 3 показана блок-схема, где наглядным образом представлено построение общей модели сигналов, исходящих из термопары и термистора.

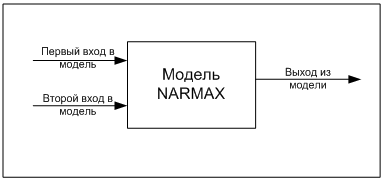
Рис. 3 - Схема модели NARMAX. К первому входу подан сигнал исходящий от термопары, ко второму входу подан сигнал, исходящий от термистора.

Столбцы матрицы коэффициентов модели сигнала термопары(a₀, a₁, …, a_n), а также столбцы матрицы коэффициентов модели сигнала термистора (b₀, b₁, …, b_n), представляют собой числовые ряды.

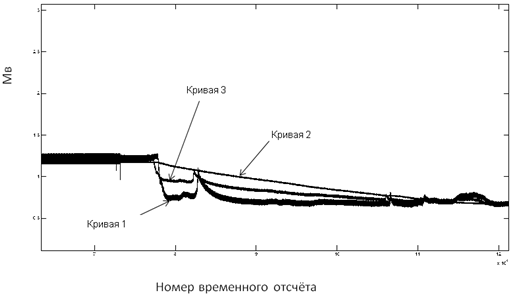
На следующем рисунке 4  представлены результаты коррекции температурных измерений термопарой и термистором при кипении воды. Кривая 1 указывает температурные измерения, полученные при помощи термопары, кривой 2 – при помощи термистора. Кривой 3 показана корректировка температурных измерений, полученная при помощи метода NARMAX с использованием общей модели NARMAX. В данном случае был применён MISO – вариант общей модели, то есть модели, которая имеет много входов в модель NARMAX и один выход из этой модели, при которой данная корректировка является выходом общей модели NARMAX. На входы в эту модель поданы температурные измерения термопарой (первый вход) и термистором (второй вход).

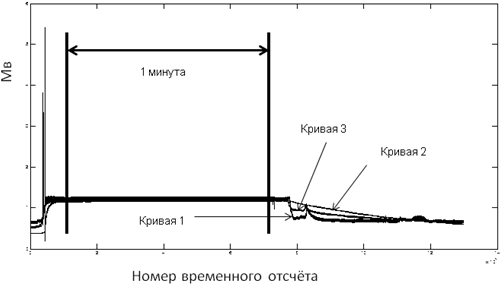
Рис. 4 - Результаты коррекции температурных измерений термопарой и термистором при кипении воды

Интервал измерений длительностью одну минуту на рисунке выделен двойной стрелкой. Характерные выдающиеся пики, представленные на рисунке, обусловлены некоторыми особенностями работы измерительных приборов. Температурные измерения проводились с частотой 1 кГц, а также были нормированы по средним значениям.

На рисунке 5 представлен процесс закипания воды более подробно.

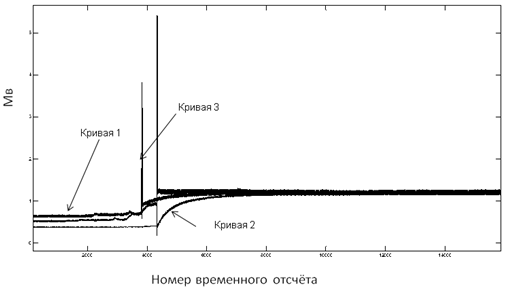
Рис. 5 - Процесс закипания воды.

На рисунке 6 представлен процесс остывания воды также более подробно.

Рис. 6 - Процесс остывания воды.

Исходя из представленных выше графиков, показанных на рисунках 4, 5 и 6 видно, что общая модель сигналов идущих с термопары и термистора позволяет градуировать и корректировать представленный датчик температуры. Соответственно, датчик температуры может работать самостоятельно, то есть без термопары. В настоящее время датчик проходит калибровку при различных температурных режимах, поэтому на оси ординат указаны нормированные значения сигналов в милливольтах.

Заключение

Проведено исследование возможностей применения метода NARMAX как метода градуирования и корректировки датчика температуры,

На основе метода NARMAX создана общая модель сигналов термопары и термистора, которая произвела соответствующую корректировку и градуирование разработанного датчика температуры.

Литература

1. Billings S.A. Orthogonal least squares methods and their application to non-linear system identification // Int. J. Control. – 1989. – V. 50. – № 5. – P. 1873–1896.
2. Лукьянов Г.Н., Рассадина А.А., Дранишникова О.А., Скирмандт Е.В., Усачев В.И. Исследование тепло- и массообменных характеристик человеческого дыхания // Приборостроение. – 2005. – № 5. – С. 68–73.
3. Лукьянов Г. Н. Полищук С. А. Нелинейное динамическое моделирование взаимосвязи процессов дыхания и сердцебиения человека на основе проведенных измерений // Науч.-технич. вестн. информационных технологий, механики и оптики . 2013. № 4 (86). С. 67–72.

References

1. Billings S.A. Orthogonal least squares methods and their application to non-linear system identification // Int. J. Control. – 1989. – V. 50. – № 5. – P. 1873–1896.
2. Luk'janov G.N., Rassadina A.A., Dranishnikova O.A., Skirmandt E.V., Usachev V.I. Issledovanie teplo- i massoobmennyh harakteristik chelovecheskogo dyhanija // Priborostroenie. – 2005. – № 5. – S. 68–73.
3. Luk'janov G. N. Polishhuk S. A. Nelinejnoe dinamicheskoe modelirovanie vzaimosvjazi processov dyhanija i serdcebienija cheloveka na osnove provedennyh izmerenij // Nauch.-tehnich. vestn. informacionnyh tehnologij, mehaniki i optiki . 2013. № 4 (86). S. 67–72.