ЭКВИВАЛЕНТНАЯ ВЕРОЯТНОСТЬ ОШИБОЧНОГО ПРИЕМА ЭЛЕМЕНТА КОДА В АДАПТИВНОЙ СИСТЕМЕ С РОС

Захарченко Н.В.¹, Бектурсунов Д.Н.², Талакевич Д.В.³, Криль А.С.⁴

¹Доктор технических наук, ²Аспирант, ³Аспирант, ⁴Кандида^т технических наук, Одесская национальная академия связи

ЭКВИВАЛЕНТНАЯ ВЕРОЯТНОСТЬ ОШИБОЧНОГО ПРИЕМА ЭЛЕМЕНТА КОДА В АДАПТИВНОЙ СИСТЕМЕ С РОС

Аннотация

Установлена зависимость между величиной эквивалентной вероятности ошибочного приема элемента кода с параметрами избыточного кода, оценено значение коэффициента уменьшения скорости в системе с обратной связью.

Ключевые слова: Передача данных (ПД), обратная связь (ОС), адаптивные системы.

Zakharchenko N.V.¹, Bektursunov D.N.², Talkayevich D.V.³, Kril A.S.⁴

¹Ph.D., ²Graduate, ³Graduate, ⁴Candidate of Technical Sciences, Odessa National Academy of Telecommunications

EQUIVALENT PROBABILITY OF WRONG RECEPTION CODE ELEMENT IN ADAPTIVE SYSTEM WITH DECISIVE FEEDBACK

Abstract

Dependence between the size of equivalent probability of wrong reception of an element of a code with parameters of an excess code is established, value of coefficient of reduction of speed in system with feedback is estimated.

Keywords: Transmission of data, feedback link, adaptive systems.

Рассмотрим условия, при которых использование обратного канала в системах передачи данных повышает их технические показатели по сравнению с  симплексными системами ПД. При этом будем полагать, что командные сигналы передаются без искажений (вероятности q_SП=q_SЛ=0), а время запаздывания сигналов t_p ≠ 0 (N_КП > 1).

В системах ПД с кодовым представлением сигналов отдельные элементы сообщения утрачивают самостоятельное информационное значение. Искажения любого элемента в виде его трансформации, пропуска или ошибочного повторения приводят к искажению всего сообщения. В тех случаях, когда особо важная информация может передаваться неоднократно, предпочтения заслуживают те методы передачи данных, которые обеспечивают малую вероятность ложных сообщений. Поэтому следует применять такие способы кодирования, при которых не обнаруживаемые ошибки вызывают бросающиеся в глаза искажения сообщений.

В этих условиях естественно использовать критерий наименьшей вероятности ошибки

\[P{}_{\text{O}\text{.}}=1-\sum\limits_{i=1}^{{{N}_{\text{}}}}{{{p}_{i}}{{p}_{ii}}}\]

(1)

где  p_i – априорная вероятность i-го элемента сообщения; p_ii – условная вероятность правильного приема i-го элемента; N_Э – число элементов сообщения. При известных p_i критерий (1) совпадает c критерием идеального наблюдателя. Если все элементы сообщения равновероятны, что характерно для систем с телекодовой передачей сигналов, то критерий (1) сводится к минимизации величины 1- p_ii, где p_ii – const для всех i = 1, 1, …, N_Э.

В системах  ПД с телекодовой передачей сигналов с  использованием помехоустойчивых кодов целесообразно использовать критерий эквивалентной   вероятности ошибки

\[{{p}_{\text{}}}=1-{{\left( 1-{{p}_{0}} \right)}^{\frac{1}{k}}}\]

(2)

характеризующий вероятность ошибки на один информационный символ помехоустойчивого (n,k)-кода. Этот критерий отвечает формализованному характеру сообщений в таких системах, поскольку он полностью абстрагируется от цены ошибки.

Критерий эквивалентной вероятности ошибки определяет условие применимости блочных корректирующих кодов в односторонних системах связи:

\[{{p}_{\text{}}}<{{p}_{\text{}}}\]

(3)

где

\[{{p}_{\text{}}}=\frac{n}{k}{{p}_{0}}{{T}_{\text{C}}}\]

(4)

p_об  – вероятность искажения символа безызбыточного кода, обеспечивающего ту же скорость передачи информации, что и данный помехоустойчивый (n,k)-код;

T_c , p₀ – длительность символа корректирующего кода и средняя вероятность его искажения.

Используя формулу для коэффициента относительной избыточности помехоустойчивого (n,k)-кода [1]

\[{{R}_{\text{}}}=\frac{n-k}{n}\]

выражения (2) и (4) можно представить в виде

\[{{p}_{\text{}}}=1-{{\left( 1-{{P}_{\text{O}\text{.}}} \right)}^{\frac{1}{n\left( 1-{{R}_{\text{}}} \right)}}}\]

(5)

\[{{p}_{\text{}}}=\frac{{{p}_{0}}{{T}_{\text{C}}}}{1-{{R}_{\text{}}}}\]

(6)

В дальнейшем будем считать более эффективной ту систему связи, которая при заданных значениях v²_ш  и υ_и обеспечивает меньшую величину p_э или при заданных v²_ш и p_э большее значение υ_и.

Для любой адаптивной системы ПД с ОС справедливо соотношение [2]

\[\underset{h_{c}^{2}\to \infty }{\mathop{\lim }}\,{{p}_{\text{}}}={{c}_{1}}p_{0}^{{{d}_{0}}}\]

(7)

где  d₀ – кодовое расстояние; c₁ – коэффициент, зависящий от способа кодирования. Например, для систем ПД с РОС, использующих в качестве сигнала S_з одну из комбинаций помехоустойчивого (n,k) -кода с обнаружением ошибок, при μ₀→∞ и h²_c>>1 вероятность

\[{{P}_{\text{O}\text{.K}}}\approx {{N}_{d}}\frac{{{2}^{k}}-2}{{{2}^{k}}-1}p_{0}^{{{d}_{0}}}\]

где N_d – число кодограмм веса d₀, и так как P_О.К=kp_Э, то коэффициент

\[c_{1}^{{}}=\frac{{{2}^{k}}-2}{2{}^{k}-1}\frac{{{N}_{d}}}{k}\]

Структура формулы (7) аналогична выражению для адаптивных систем ПД с организацией симплексного режима работы и применением  корректирующих кодов. Это позволяет при определении условий применимости  принципа  обратной  связи  воспользоваться  методом Л.М. Финка, разработанным для указанных выше систем, и, в частности, критерием p_Э<p_об.

При некогерентном приеме двоичных ортогональных сигналов вероятность искажения символа

\[{{p}_{\text{0}}}=\frac{1}{2}{{\text{e}}^{-\frac{h_{c}^{2}}{2}}}\]

Тогда, согласно выражению (7) эквивалентная вероятность ошибки будет определяться

\[{{p}_{\text{}}}=\frac{{{c}_{1}}}{{{2}^{{{d}_{0}}}}}{{\text{e}}^{-\frac{{{d}_{0}}h_{c}^{2}}{2}}}\]

С учетом повторений превышение сигнала в адаптивной системе ПД с ОС

\[h_{c\text{ }\!\!\mu\!\!\text{ }}^{2}=\frac{h_{c}^{2}}{1-{{R}_{\text{}\text{.}}}}\]

(8)

Тогда вероятность обнаружения ошибки

\[{{p}_{\text{}}}=\frac{1}{2}{{\text{e}}^{-\frac{h_{c\text{ }\!\!\mu\!\!\text{ }}^{2}}{2}}}=\frac{1}{2}{{\left( 2{{p}_{0}} \right)}^{\frac{1}{1-{{R}_{\text{}\text{.}}}}}}\]

откуда

\[\underset{h_{c}^{2}\to \infty }{\mathop{\lim }}\,\frac{{{p}_{\text{}}}}{{{p}_{\text{}}}}=\frac{{{c}_{1}}}{{{2}^{{{d}_{0}}-1}}}{{\text{e}}^{{{\frac{1}{1-R}}_{\text{}\text{.}}}-{{d}_{0}}}}\]

(9)

Отсюда следует, что условие (3) выполняется, если коэффициент

\[{{\text{ }\!\!\eta\!\!\text{ }}_{\upsilon }}=\frac{1}{1-{{R}_{\text{}\text{.}}}}<{{d}_{0}}\]

(10)

При идеальной обратной связи коэффициент  имеет минимальное значение, для скорости передачи при μ̅=1, а условие (10) принимает вид

\[\frac{n}{k}<{{d}_{0}}\]

(11)

Это выражение показывает, что при идеальной обратной связи и h²_c>>1 подавляющее большинство обнаруживаемых кодов обеспечивает выполнение неравенства (11). Это означает, что помехоустойчивость адаптивных систем ПД с ОС будет выше, чем систем без обратной связи с безызбыточным кодированием при одинаковой скорости передачи информации.

При запаздывании сигналов условие (3) может не выполняться даже для достаточно мощных кодов, так как с увеличением N_КП коэффициент R_И.О возрастает [3].

\[{{R}_{\text{}\text{.}}}=1-\frac{1-{{R}_{\text{}\text{.}}}}{1+(\overline{\text{ }\!\!\mu\!\!\text{ }}-1){{N}_{\text{}\text{.}}}}\]

откуда коэффициент уменьшения скорости передачи информации в адаптивной системе ПД с ОС

\[{{\text{ }\!\!\eta\!\!\text{ }}_{\upsilon }}=\frac{1+\left( \overline{\text{ }\!\!\mu\!\!\text{ }}-1 \right){{N}_{\text{}\text{.}}}}{1-{{R}_{\text{}\text{.}}}}\]

Тогда вместо неравенства (10) имеем

\[\frac{1+\left( \overline{\text{ }\!\!\mu\!\!\text{ }}-1 \right){{N}_{\text{}\text{.}}}}{1-{{R}_{\text{}\text{.}}}}<{{d}_{0}}\]

или

\[\left( \overline{\text{ }\!\!\mu\!\!\text{ }}-1 \right){{N}_{\text{}\text{.}}}<{{d}_{0}}\left( 1-{{R}_{\text{}\text{.}}} \right)-1\]

(12)

Если при μ→∞ выполняется условие np₀<<1, то формулу (12) можно представить в виде

\[n{{p}_{0}}{{N}_{\text{}\text{.}}}<\frac{k{{d}_{0}}}{n}-\text{1}\]

(13)

Если запаздывание сигналов определяется в основном временем их распространения, то справедливо неравенство

\[2{{t}_{\text{p}}}{{\upsilon }_{\text{T}}}<\frac{k{{d}_{0}}}{n}-\text{1}\]

(14)

Это неравенство наглядно показывает влияние запаздывания сигналов. Однако его выполнение зависит не только от уровня шумов в канале связи, но и от обнаруживающей способности кода. Так, для линейных двоичных кодов должны выполняться условия Плоткина:

\[\left( n-k \right)\ge 2\left( {{d}_{0}}-1 \right)-{{\log }_{2}}{{d}_{0}}\]

\[n\ge 2{{d}_{0}}-1\]

(15)

Согласно неравенствам (15), изменение n в широких пределах сравнительно слабо влияет на правую часть выражения (14). Например, при

N=3…127 величина  возрастает от 0,35 до 2,62. Из соотношения (13) также следует, что чем больше произведение t_pυ_T, тем меньше допустимое значение вероятности p₀. При малых значениях t_pυ_T, когда при n_s=n неравенство  не выполняется, левая часть выражения (13) не зависит от  и, следовательно, с ростом  увеличиваются обе части выражения (14). Наконец, если не выполняется условие  np₀<<1, то левая часть неравенства (14) возрастает с увеличением n быстрее правой части.

Таким образом, анализ выражения (13) в общем виде затруднителен. Однако чем лучше при k=const  удовлетворяется это неравенство за счет увеличения n, тем сильнее зависит левая его часть от уровня помех в канале связи. Наоборот, при использовании кодов с малым d₀ условие (13) выполняется при изменении p₀ в более широких границах. Следовательно, чем больше отношение , тем меньше нижняя граница вероятности p_об=p_0min, обеспечивающая выполнение условия (3).

Следуя методу Л.М. Финка, найдем уравнение асимптоты кривой . Для отыскания этой зависимости воспользуемся выражением (12) при h²_c>>1:

\[\frac{{{p}_{\text{}}}}{{{p}_{\text{}}}}=\frac{{{c}_{1}}}{{{c}^{{{d}_{0}}-1}}}{{\left( 2{{p}_{0}} \right)}^{\frac{{{d}_{0}}-{{d}_{0}}{{R}_{\text{}\text{.}}}-1}{1-{{R}_{\text{}\text{.}}}}}}\],

откуда уравнение асимптоты имеет вид

\[{{\log }_{10}}\frac{{{p}_{\text{}}}}{{{p}_{\text{}}}}={{\log }_{10}}\frac{{{c}_{1}}}{{{c}^{{{d}_{0}}-1}}}+\frac{{{d}_{0}}-{{d}_{0}}{{R}_{\text{}\text{.}}}-1}{1-{{R}_{\text{}\text{.}}}}{{\log }_{10}}\left( 2{{p}_{0}} \right)\]

(16)

Угловой коэффициент асимптоты

\[{{\xi }_{a}}=\frac{{{d}_{0}}-{{d}_{0}}{{R}_{\text{}\text{.}}}-1}{1-{{R}_{\text{}\text{.}}}}=\frac{k{{d}_{0}}-n}{k}\]

(17)

Условие применимости обратной связи (11) эквивалентно условию

\[{{\text{ }\!\!\xi\!\!\text{ }}_{a}}>0\]

(18)

Граничное значение вероятности искажения кодовых символов определяется из уравнения

\[{{\log }_{2}}{{p}_{0\min }}=\frac{{{d}_{0}}-1}{{{\text{ }\!\!\xi\!\!\text{ }}_{a}}}-\frac{1}{{{\text{ }\!\!\xi\!\!\text{ }}_{a}}}{{\log }_{2}}{{c}_{1}}-1\]

(19)

Так как для оптимальных обнаруживающих кодов n≈2d₀, то параметр d₀ в выражениях (18) и (19) можно исключить и выра­зить ξ_a и p_0min через  и k. В частности, для циклических кодов 2d₀=n+1 и

\[{{\text{ }\!\!\xi\!\!\text{ }}_{a}}=\frac{k\left( n+1 \right)-2n}{2k}\]

\[{{\log }_{2}}{{p}_{0\min }}=\frac{1}{{{\text{ }\!\!\xi\!\!\text{ }}_{a}}}\left( \frac{n-1}{2}-{{\log }_{2}}\frac{n-1}{k} \right)\]

(20)

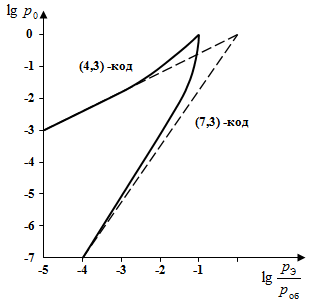
На рис. 1 показаны графики зависимости  и их асимптоты для обнаруживающего эквидистантного (7,3)-кода и (4,3)-кода c проверкой на четность. Из рисунка видно, что выражение (16) удовлетворительно аппроксимирует зависимость и позволяет определить вероятность p_0min, но при достаточно больших значениях вероятности p_об.

Рис. 1 – Применимость принципа обратной связи

Литература

1. Захарченко Н.В., Рудый Е.М., Вараксин А.А., Мамедов М.А., Гаджиев М.М.. Эффективные системы передачи информации./Под ред. академика МАИ, доктора техн. наук, проф. Н.В. Захарченко. – Баку «ЭЛМ», 2007, 568 с.
2. Системы электросвязи: Учебник для вузов/В.П. Шувалов, С.И. Горшкова, Г.П. Катунин и др.; Под ред. В.П. Шувалова. – М.: Радио и связь, 1987.
3. Коричнев Л.П., Королев В.Д. Статистический контроль каналов связи. – М.: Радио связь, 1989. – 240 с.

References

1. Zakharchenko N. V., Rudnyi E.M., Varasin A.A., Mamedov M.A., Gadzhiev M.M., Effective systems of information transfer. / Under the editorship of the academician of MAI, the doctor tech. sciences, prof. N.V. Zakharchenko. – Baku "ELM", 2007, 568 pages.
2. Systems of telecommunication: The textbook for higher education institutions/V.P. Shuvalov, S. I. Gorshkova, G. P. Katunin, etc.; Under the editorship of V.P. Shuvalov. – M.: Radio and communication, 1987.
3. Korichnev L.P., Korolev V.D., Static control of communication channels – M.: Radio communication, 1989. – 240 pages.