ЭКОНОМИКО-СТАТИСТИЧЕСКИЙ АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ ВЛИЯНИЯ ЭТНИЧЕСКИХ ЭЛЕМЕНТОВ ДИЗАЙНА НА СПРОС ОБУВИ

Зинюк О.В.

Кандидат технических наук, Московский гуманитарный университет

ЭКОНОМИКО-СТАТИСТИЧЕСКИЙ АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ ВЛИЯНИЯ ЭТНИЧЕСКИХ ЭЛЕМЕНТОВ ДИЗАЙНА НА СПРОС ОБУВИ

Аннотация

В статье рассматривается экономико-статистический анализ данных о реализованной обуви, полученных в результате популяризации обуви по элементам этно-дизайна. Используются методики корреляционного анализа параметров выборки, которые не требуют знания закона распределения. Полученные результаты могут быть использованы для формирования перспективного ассортимента в соответствии с коэффициентами корреляционного отношения.

Ключевые слова: этно-дизайн, покупательский спрос, корреляционный анализ.

Zinyuk O.V.

Candidate of Technical Sciences, the Moscow University for the Humanities

ECONOMIC AND STATISTICAL ANALYSIS OF THE RESULTS THE IMPACT OF ETHNIC DESIGN ELEMENT ON DEMAND FOR SHOES

Abstract

The article deals with economic and statistical analysis of data on sales of footwear resulting popularization shoe on the elements of ethno-design. Using the procedure of correlation study between the samples that do not require knowledge of the distribution law. The results can be used to form perspective range in accordance with coefficients of correlation ratio.

Keywords: ethno-design, customer demand, the correlation analysis.

В рамках формирования современной ценовой и ассортиментной стратегии рынка обуви актуальность приобретают методы стимулирования сбыта, а также способы оценки эффективности их использования.

В статье представлены результаты экономико-статистического анализа данных о количестве заказанной обуви, которые получены после проведения маркетингового исследования, основывающегося на популяризации современной обуви по элементам этно-дизайна.

Экономико-статистический анализ данных проводится по методике расчета ошибки выборки, проверки ее однородности и нормальности, а также определения корреляционного отношения, в которой используются теоретические данные, не требующие знания закона распределения, и средства автоматизации расчетов MS Excel и VBA [1, 2].

В качестве исходных данных рассматриваются две выборки, полученные в результате сбора информации на разработанном и опубликованном сайте «Ваша обувь! Ваша история!» в течение 20 контрольных дней.

Первая выборка представляет собой сформированный для обработки в Excel двумерный массив количества заказов моделей женской обуви, которые отобраны из действующего ассортимента интернет-магазина и позиционированы как отражающие национальные особенности обуви различных этносов. Вторая выборка является результатом сбора информации по принадлежности заказчиков к возрастным группам (от 15 до 29 лет, от 30 до 49 лет, от 50 до 64 лет).

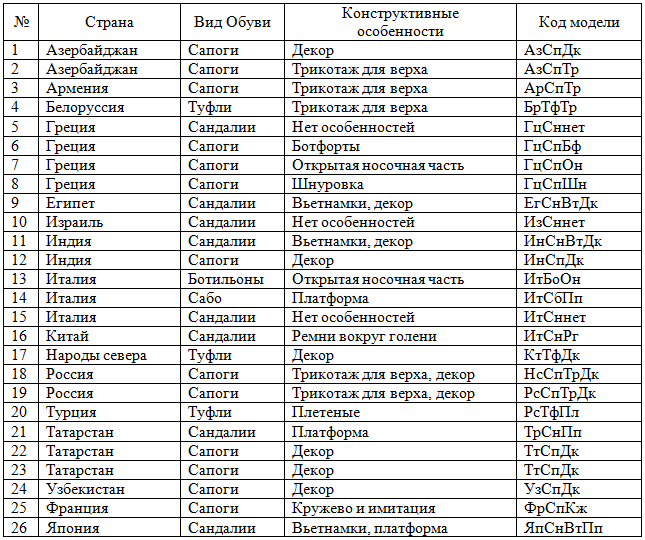
Для формализации данных с целью их дальнейшей обработки моделям присвоены классификационные коды, включающие страну, вид обуви и ее конструктивные особенности (табл. 1). Виды обуви являются традиционными для женского ассортимента; страны отобраны по принципу наибольшего влияния конструктивных особенностей их этнической обуви на современную моду.

Таблица 1 - Классификационные коды моделей

Каждая выборка содержит номер измерения от 1 до 20 (по количеству дней), общее количество заказов в день и количество заказов обуви по этно-факторам и возрастным параметрам.

Для выявления количественной зависимости между общим объемом заказов и данными по этно-факторам и возрасту необходимо провести корреляционный анализ выборки по следующему алгоритму.

1. Расчет ошибки выборки для выявления ее репрезентативности, который проводится по величине доверительного интервала [3].
2. Определение однородности генеральной совокупности и выборок по факторам. Для оценки однородности вычисляется модуль статистики [3]. Далее проводится сравнение значения модуля статистики с граничным значением (в экономико-статистических исследованиях наиболее распространено значение 1,96). Если полученное значение не превышает граничное, то можно говорить о наличии однородности выборки. В алгоритм оценки однородности выборки входит также определение допустимого расхождения между частотами, которое показывает, при каком максимальном расхождении частот все еще делается вывод о том, что верна гипотеза однородности.
3. Проверка нормальности распределения с целью выбора параметрических или непараметрических критериев статистики для оценки выборки. Проверка нормальности распределения проводится средствами MS Excel [4] по результатам сравнения среднего, медианы и моды (при нормальном распределении они должны совпадать) и оценке эксцесса (нулевое значение говорит о нормальности) [5].
4. Выбор метода корреляционного анализа. Для количественного анализа взаимосвязи между генеральной совокупностью (общим количеством заказов) и количеством заказов обуви по факторам необходимо сделать выбор между параметрической и непараметрической оценкой, то есть использованием коэффициента корреляции при наличии нормальности или корреляционного отношения, которое фиксирует наличие любой связи между признаками [3].

Для минимизации повторяющихся операций при формировании встроенных функций Excel и выполнении групповых операций, связанных с использованием для оценки однородности и корреляционного анализа не фиксированных значений, а интервалов, использованы средства автоматизации расчетов в виде разработанных пользовательских функций на языке VBA [1, 2]. Функциональное назначение функций: «Chastota» – расчет допустимого отклонения между частотами; «Interval» – определение номера интервала выборки при расчете корреляционного отношения, «Normal» – вычисление абсолютных отклонений среднего значения от медианы и моды, «Oshibka» – расчет ошибки выборки, «Statistika» – определение модуля статистики.

С целью визуализации полученных результатов и исключения ручных операций по переносу значений и позиций ячеек рабочего листа в зоны последующих расчетов используются разработанные на VBA макросы [1, 2]. Назначение макросов: «ClearSelection» – очистка выделенного диапазона ячеек от цвета, «GetMaxMin» – поиск максимального и минимального значения диапазона, «Perenos_znach» – перенос значений из ячеек с максимальными и минимальными пофакторными значениями в отдельную зону рабочего листа, «SetPosition» – перенос позиций ячеек с наибольшим расхождением частот в таблицу исходных данных, «SearchMaxMin» – выделение цветом ячеек с максимальными и минимальными значениями.

Исходными данными для расчета ошибки выборки являются суммарные значения общего и пофакторного количества заказов, полученные по данным табл. 1, а также процент пофакторных сумм от общей. Анализ результатов расчета ошибки выборки с помощью пользовательской функции «Oshibka» показывает, что в абсолютном выражении ошибка выборки по этно-факторам лежит в интервале [0,28-0,40] (не превышает одну пару обуви), по возрасту – [0,10-0,12] (не превышает одного человека), что позволяет сделать вывод о репрезентативности выборки и использовать ее для дальнейшего экономико-статистического анализа.

В маркетинге проверка однородности биноминальных выборок важна для сегментации рынка. Если две группы не отличаются по ответам, значит, их можно объединить в один сегмент и проводить по отношению к ним одну и ту же маркетинговую политику, в частности, осуществлять одни и те же рекламные воздействия [2]. В рассматриваемых базах данных, отсортированных по возрастанию общего количества заказов, для проверки однородности проводятся следующие операции.

1. Поиск попарных значений количества заказов с наибольшим расхождением частот (макрос «SearchMaxMin»).
2. Перенос найденных позиций ячеек с наибольшим расхождением частот на соответствующие ячейки исходных таблиц после сортировки (макрос «SetPosition») и для удобства проведения дальнейших расчетов перенос значений из ячеек с максимальными и минимальными пофакторными значениями в отдельную зону рабочего листа (макрос «Perenos_znach») (табл. 2).
3. Расчет модуля статистики |Q| с использованием функции «Statistika») (табл. 2, 3).

Таблица 2 - Минимальные и максимальные значения, модуль статистики |Q| по этно-факторам (ЭФ)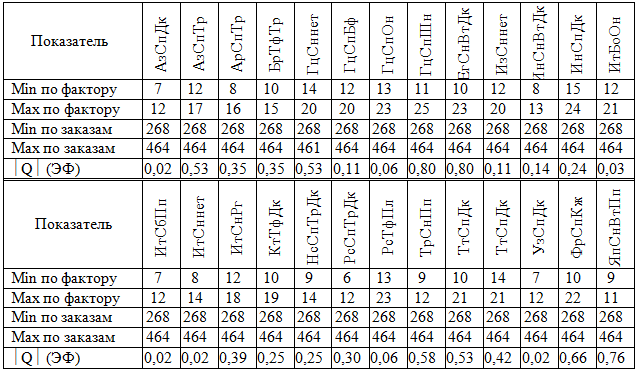

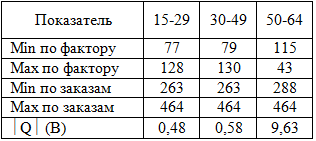
Таблица 3 - Минимальные и максимальные значения, модуль статистики |Q| по возрасту (В)

Полученное максимальное значение |Q| по этно-факторам (равное 0,80) меньше 1,96, в связи с чем можно сделать вывод об однородности всех групп, участвующих в экспертном опросе. По возрасту однородными являются группы от 15 до 29 и от 30 до 49 лет, для которых |Q| равно соответственно 0,48 и 0,58, тогда как группа заказчиков от 50 до 64 лет является крайне неоднородной (|Q| = 9,63).

4. Расчет допустимого расхождения между частотами с использованием функции «Chastota».

Для рассматриваемых в работе данных по этно-факторам интервал колебания допустимого отклонения между частотами составляет [0,023-0,034] или [2,3-3,4%] для уровня значимости 0,05. Таким образом, для выбранного уровня значимости отличие частот менее чем на 3,4% показывает, что для выборок по этно-факторам различие не обнаружено. Для данных по возрасту интервал колебания допустимого отклонения между частотами составляет [0,06-0,07] или [6,0-7,0%] для уровня значимости 0,05. В данной выборке для выбранного уровня значимости допустимое отклонение частот превышает показатель по этно-факторам более чем в два раза.

Вычисление среднего, медианы, моды и эксцесса для проверки выборки на нормальность проводится с использованием встроенных функций MS Excel: =СРЗНАЧ(), =МЕДИАНА(), =МОДА(), =ЭКСЦЕСС(). Для расчета абсолютных отклонений среднего значения от медианы и моды используется пользовательская функция «Normal». Анализ отклонений среднего значения от медианы и моды показывают, что перечисленные величины не совпадают, а эксцесс кривой распределения отличен от нуля как для выборок по этно-факторам, так и по возрасту. Полученные результаты позволяют сделать вывод о том, что распределение рассматриваемых выборок не подчиняется нормальному (гауссовому) закону распределения и позволяют использовать для анализа только непараметрические критерии статистики [5].

Для количественного анализа эффективности маркетинговых мероприятий необходимо установить зависимость между генеральной совокупностью (общим количеством заказов) и количеством заказов обуви по этно-факторам и по возрасту. Отсутствие нормальности выборок делает невозможным использование коэффициента корреляции, который предполагает наличие линейной связи между признаками. В таких случаях для выявления связи применяют другой показатель – корреляционное отношение [6], которое фиксирует наличие любой связи между признаками.

Алгоритм расчета корреляционного отношения включает следующие шаги.

1. Область значений генеральной совокупности (общего количества заказов) разбивается на интервалы (функция «Interval»).
2. Для каждого интервала определяется среднее значение количества заказов по каждому этно-фактору и возрастной группе.
3. Далее вычисляется корреляционное отношение, величина которого, как и коэффициента корреляции, лежит между нулем и единицей; чем ближе значение корреляционного отношения к единице, тем более тесной является связь.

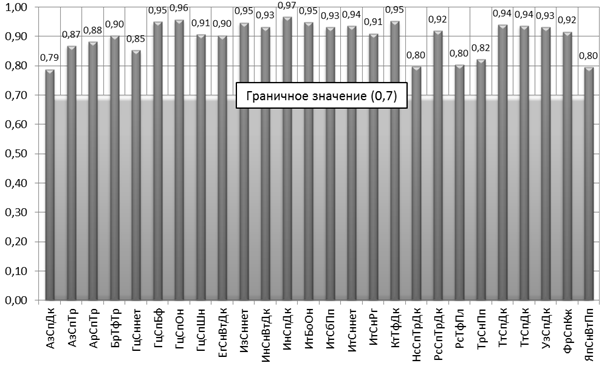
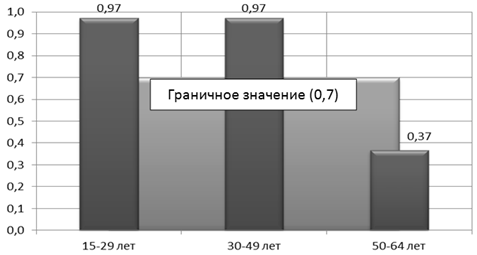
Полученные данные сводятся в единые базы для проведения расчета межгрупповой, общей, внутренней дисперсии и корреляционного отношения.Графический анализ пофакторного коэффициента корреляционного отношения (рис. 1) показывает, что этно-факторы имеют высокую (0,7-0,9) и весьма высокую (0,9-0,97) по шкале Чеддока [6] функциональную связь с общим количеством заказов. Значения корреляционного отношения по возрасту (рис. 2) имеют весьма высокую (0,97) функциональную связь с общим количеством заказов в группах респондентов от 15 до 29 и от 30 до 49 лет, тогда как в возрастном диапазоне от 50 до 64 лет корреляционное отношение составляет 0,37, то есть данная группа не имеет функциональной связи с общим количеством заказов.

Рис. 1 - Значение корреляционного отношения по этно-факторам

Рис. 2 - Значение корреляционного отношения по возрасту

При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации [6] всегда будет ниже 50 %. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя (общего количества заказов обуви). Таким образом, формирование маркетинговой политики необходимо проводить только на основании высокого и весьма высокого корреляционного отношения. В противном случае они могут быть ошибочны и не достоверны. Из рассматриваемых параметров все этно-факторы могут учитываться при разработке маркетинговой стратегии, тогда как разделение заказчиков на целевые группы по возрасту не целесообразно, так как при весьма высоком корреляционном отношении в группах от 15 до 29 и от 30 до 49 лет, группа от 50 до 64 лет выпадает из возможности дальнейших исследований. Полученные результаты объясняются тем, что проводимое исследование базируется на модельном ряду, составленном на основании модных тенденций, которые для заказчиков старше 50-ти лет не являются приоритетными по сравнению с комфортностью обуви и ее эксплуатационными качествами.

Полученные результаты могут быть использованы для корректировки количества моделей обуви при формировании перспективного ассортимента в соответствии с коэффициентами корреляционного отношения.

Литература

1. Зинюк О.В. Методика расчета ошибки и однородности выборки средствами MS EXCEL и VBA // Экономика, статистика и информатика. Вестник УМО. 2011. №4. С.84-88.
2. Зинюк О.В. Проверка выборки на нормальность и расчет корреляционного отношения в среде MS EXCEL и VBA // Экономика, статистика и информатика. Вестник УМО. 2011. №5. С.109-114.
3. Орлов А.И. Прикладная статистика. М.: Экзамен, 2006. 672 с.
4. Лялин В. С., Зверева И. Г., Никифорова Н. Г. Название: Статистика. Теория и практика в Excel. Издательство: Финансы и статистика, Инфра-М, 2010. 448 с.
5. Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Юрайт, 2011. 480 с.
6. Громов Е.И., Гладилин А. В., Герасимов А. Н. Эконометрика. М.: Феникс, 2011. 304 с.

References

1. Zinjuk O.V. Metodika rascheta oshibki i odnorodnosti vyborki sredstvami MS EXCEL i VBA // Jekonomika, statistika i informatika. Vestnik UMO. 2011. №4. S.84-88.
2. Zinjuk O.V. Proverka vyborki na normal'nost' i raschet korreljacionnogo otnoshenija v srede MS EXCEL i VBA // Jekonomika, statistika i informatika. Vestnik UMO. 2011. №5. S.109-114.
3. Orlov A.I. Prikladnaja statistika. M.: Jekzamen, 2006. 672 s.
4. Ljalin V. S., Zvereva I. G., Nikiforova N. G. Nazvanie: Statistika. Teorija i praktika v Excel. Izdatel'stvo: Finansy i statistika, Infra-M, 2010. 448 s.
5. Gmurman V. E. Teorija verojatnostej i matematicheskaja statistika. M.: Jurajt, 2011. 480 s.
6. Gromov E.I., Gladilin A. V., Gerasimov A. N. Jekonometrika. M.: Feniks, 2011. 304 s.