Численное моделирование притока к горизонтальному окончанию газовой скважины
Численное моделирование притока к горизонтальному окончанию газовой скважины
Аннотация
В настоящее время теоретические основы применения горизонтальных скважин с разными траекториями ствола на газовых месторождениях не полностью разработаны, поэтому прогнозирование их производительности не может быть оценено с необходимой достоверностью. На основании этого в работе рассматривается совместное решение уравнений притока и распределения давления вдоль пологого и волнообразного ствола газовой скважины, работающей на установившемся режиме. Оценка проводилась в газовом продуктивном пласте с непроницаемыми кровлей и подошвой. Для изучения влияния фильтрационно-емкостных параметров пласта на работу газовой скважины с учетом траектории ствола, его длины и типа заканчивания в статье предлагается методика расчета дебитов сегментов пологого и волнообразного стволов, которая позволяет определять эпюру скоростей фильтрации и учитывать распределение давления и развивающийся поток по ее стволу. В итоге на основе моделирования работы скважины сложного профиль получена система линейных алгебраических уравнений, решением которой являются дебиты участков горизонтальной газовой скважины произвольной траектории.
1. Введение
При определении производительности горизонтальной газовой скважины необходимо совместно решать уравнения притока и распределения давления вдоль ствола газовой скважины с протяженным горизонтальным окончанием . Для вертикальной скважины предположение о постоянстве забойного давления допустимо, поскольку интервал перфорации сравнительно мал по сравнению с ее длиной. В настоящее время разработано множество формул для описания установившегося притока к горизонтальным газовым скважинам , , , .
Для горизонтальной газовой скважины определение забойного давления крайне важно , так как длина горизонтального участка намного больше толщины пласта. По мере того как флюид течет от конечного горизонтального участка (носок), к началу горизонтального участка ствола скважины (пятка), включая потери давления на трение , что вызывает перепад давления в горизонтальном участке ствола скважины по всей длине. Также промысловый опыт и исследования расходомеров на скважинах длинных горизонтальных участков показали, что потери давления на трение в стволе скважины являются существенным фактором, ограничивающим эффективность ее ствола и, следовательно, снижающим производительность. На основании этого потери давления на трение могут быть сопоставимы с депрессией в конце разработки, что делает крайний сегмент горизонтального ствола скважины непродуктивной . Следовательно, нельзя предположить, что давление в стволе скважины будет постоянным по длине горизонтального участка. Кроме того, в большинстве моделей, описывающих приток к горизонтальной газовой скважине ошибочно представляется, что горизонтальный ствол скважины абсолютно горизонтален, и не учитывается, что почти каждая скважина имеет определенную степень волнистости вдоль траектории своего ствола.
В работе предложен подход для определения изменения давления в стволе и притока по длине ствола пологой и волнообразной скважин, не полагаясь на нереалистичное предположение о постоянном давлении в стволе скважины. Объектом применения скважин такой конструкции является газоносный продуктивный пласт с непроницаемыми кровлей и подошвой (см. рисунок 1).
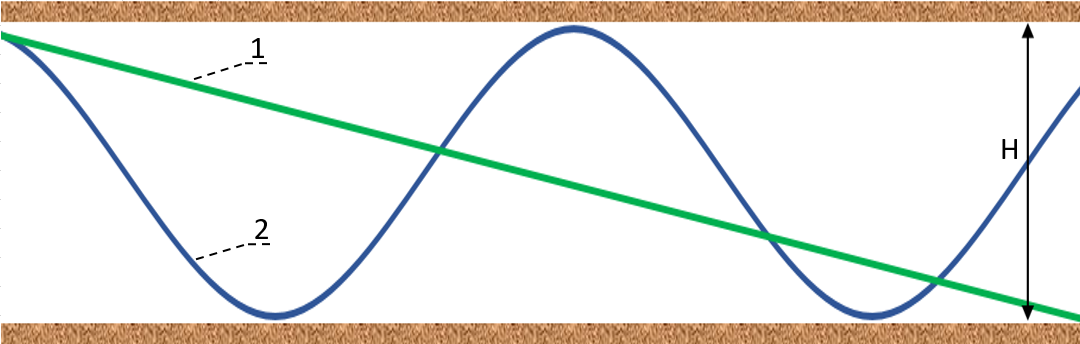
Рисунок 1 - Траектория скважин пологого (1) и волнообразного профиля (2) в газоносном продуктивном пласте мощностью Н
2. Материалы и методы исследования
Методики, используемые для анализа продуктивности скважин, делятся на два основных подхода: численное моделирование и аналитические решения. В большинстве моделей для численного моделирования падение давления в стволе скважины не рассматривается, что может привести к неверным прогнозам производительности скважины.
Аналитические модели для определения технологических показателей скважины хорошо изучены для вертикальных, горизонтальных и наклонно-направленных скважин, которые с некоторыми допущениями связывают между собой дебит и изменение давления в стволе скважины. Однако геометрия коллектора и фактические конструкции скважин обычно намного сложнее, чем предположения, предусмотренные в данных моделях.
По предыдущим работам определено, что фильтрация газа к горизонтальным скважинам может происходить по линейному закону , , . В работах С.К. Сохошко показано, что при длине горизонтального окончания более 100 м значение числа Рейнольдса в большинстве случаев становится меньше критического (Reк), что можно использовать решения, полученные для притока нефти, заменив давление на функцию Лейбензона, а объемный расход на массовый, следуя И.А. Чарному .
Рассмотрим развивающийся поток в стволе газовой скважины, оборудованной фильтром-хвостовиком.
Массовый расход газа j-го отверстия обозначим mj. Тогда массовый расход в стволе на уровне j-го отверстия определится:
В работе приведено решение для распределения давления вдоль сегментов газовой скважины:
где
Pн — давление на контуре питания, Па;
Pк — забойное давление, Па;
М — массовый расход газа, кг/с;
λ — коэффициент гидравлического сопротивления участка ствола, б/р;
z — коэффициент сверхсжимаемости газа, б/р;
R — универсальная газовая постоянная, Дж/(кг×К);
T — температура потока газа, К;
L — длина рассматриваемого участка ствола, м;
b — коэффициент, учитывающий геометрию ствола, б/р;
c — коэффициент, учитывающий изменение скорости газа, б/р;
f — площадь поперечного сечения ствола, м2;
D — внутренний диаметр ствола, м.
Как было предложено в работе в стволе скважины возникают гидравлические потери на местные сопротивления. Участки без отверстий имеют гидравлическое сопротивление λ1, а участки с отверстиями имеют гидравлическое сопротивление λ2.
Для получения распределения давления в однородно-анизотропном пласте и переходу от давления к функции Лейбензона можно использовать теорию потенциала точечного стока . Для точечных стоков, работающих в газоносном пласте и моделирующих приток к сегментам ствола скважины, получена система уравнений:
где
mi — массовый дебит i-го отверстия, кг/с;
µ — динамическая вязкость газа, Па⋅с;
xj и zj — координаты точек, в которых определяется функция Лейбензона, м;
xi и zi — координаты сегментов скважин, м;
H — толщина пласта, м;
kh — проницаемость пласта по горизонтали, м2;
kz — проницаемость пласта по вертикали, м2;
N — число сегментов, ед.;
xk = yk — расстояние до контура питания, м.
Для расчета профиля притока к стволу газовой скважины, т.е. массовых дебитов сегментов mi, необходимо совместно решить уравнения (2) и (3), для каждого сегмента соответственно, делая переход от давления к функции Лейбензона и обратно . Данная система уравнений решается методом итераций после задания начального распределения массовых расходов отверстий вдоль ствола.
В данной работе объектом исследования являются две скважины — первая с пологой траекторией ствола, а вторая с волнообразной траекторией, расположенных в однородно-анизотропном газоносном пласте с непроницаемыми кровлей и подошвой, с постоянным давлением на контуре питания (Rк).
В таблице 1 представлено расположение по глубине интервала вскрытия. Также на рисунке 2 показан разрез газоносного пласта, в котором оценена работа двух скважин с разными профилями ствола.
Таблица 1 - Исходные данные
Пласт | Кровля пласта | Подошва пласта | ||||||||||
MD (измеренная глубина) | TVD (абсолютная глубина) | SSTVD (абсолютная глубина от уровня моря) | MD (измеренная глубина) | TVD (абсолютная глубина) | SSTVD (абсолютная глубина от уровня моря) | |||||||
м | фут | м | фут | м | фут | м | фут | м | фут | м | фут | |
Т5 | 2910,2 | 9548,2 | 2169,3 | 7117,2 | 2151,3 | -7058,1 | 3090,7 | 10140,2 | 2188,5 | 7180,0 | 2170,4 | -7120,9 |
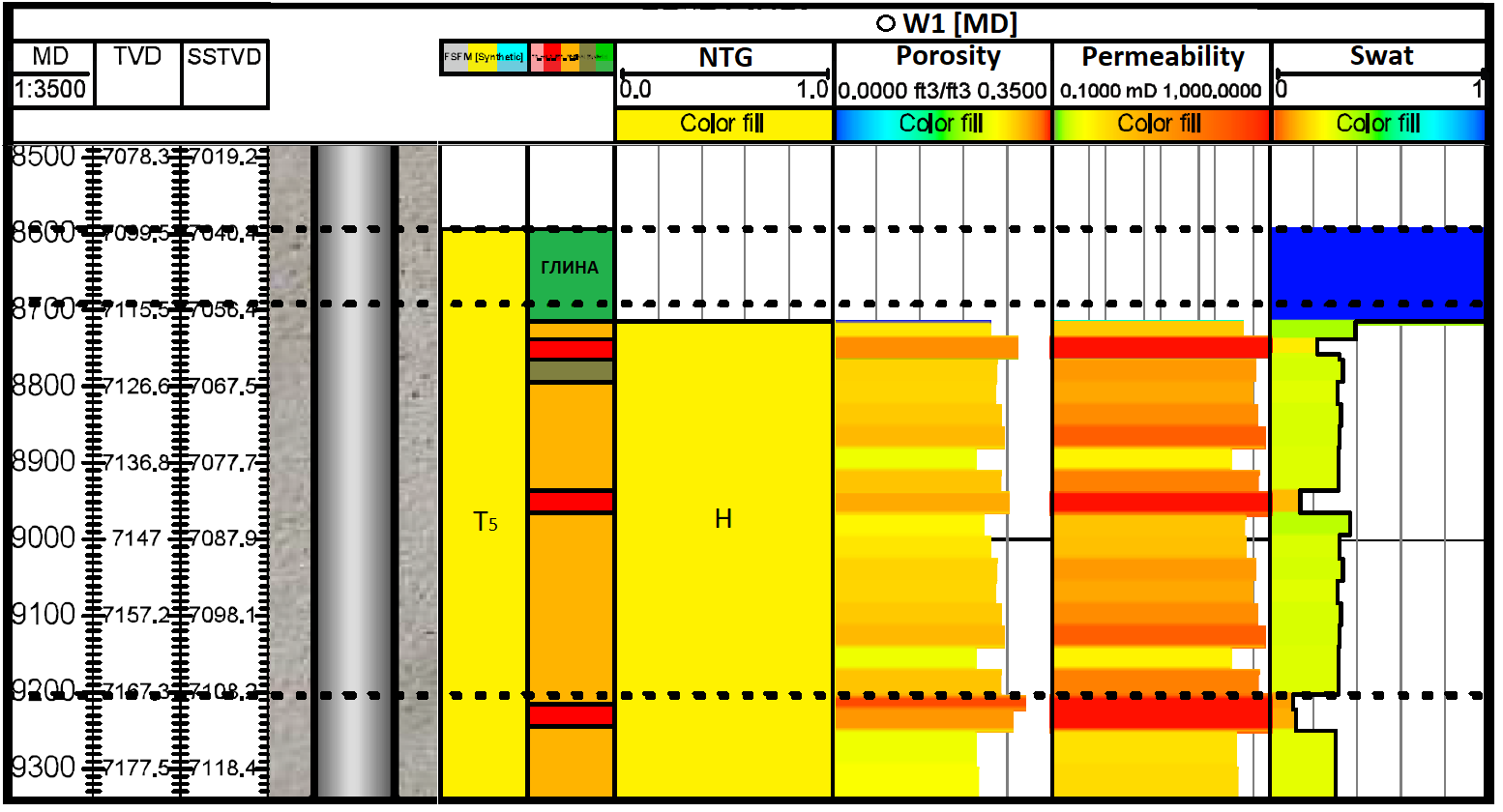
Рисунок 2 - Разрез скважины W1:
MD – измеренная глубина; TVD – абсолютная глубина; SSTVD – абсолютная глубина от уровня моря; NTG – коэффициент доли коллектора; Swat – водонасыщенность
Таблица 2 - Исходные данные для исследуемого сценария
Параметр | Значение |
Пластовое давление, МПа | 28 |
Проницаемость по горизонтали, м2 | 5,15214e-10 |
Проницаемость по вертикали, м2 | 5,1324e-11 |
Пористость, % | 25 |
Эффективная толщина пласта (H), м | 19 |
Вязкость, Па⋅с | 0,000023 |
Внутренний диаметр, мм | 140 |
Длина сегмента скважины, м | 20 |
Длина ствола, м | 180 |
3. Результаты исследований и их обоснование/обсуждение
Проведён расчёт профиля притока к пологой и волнообразной траектории ствола газовой скважины со следующими параметрами: толщина пласта 19 м, угол наклона к вертикали (зенитный угол) 85°, длина ствола пологой и волнообразной скважин составляет 180 м, весь интервал пласта находящийся между кровлей и подошвой обеих скважин оборудован фильтром-хвостовиком.
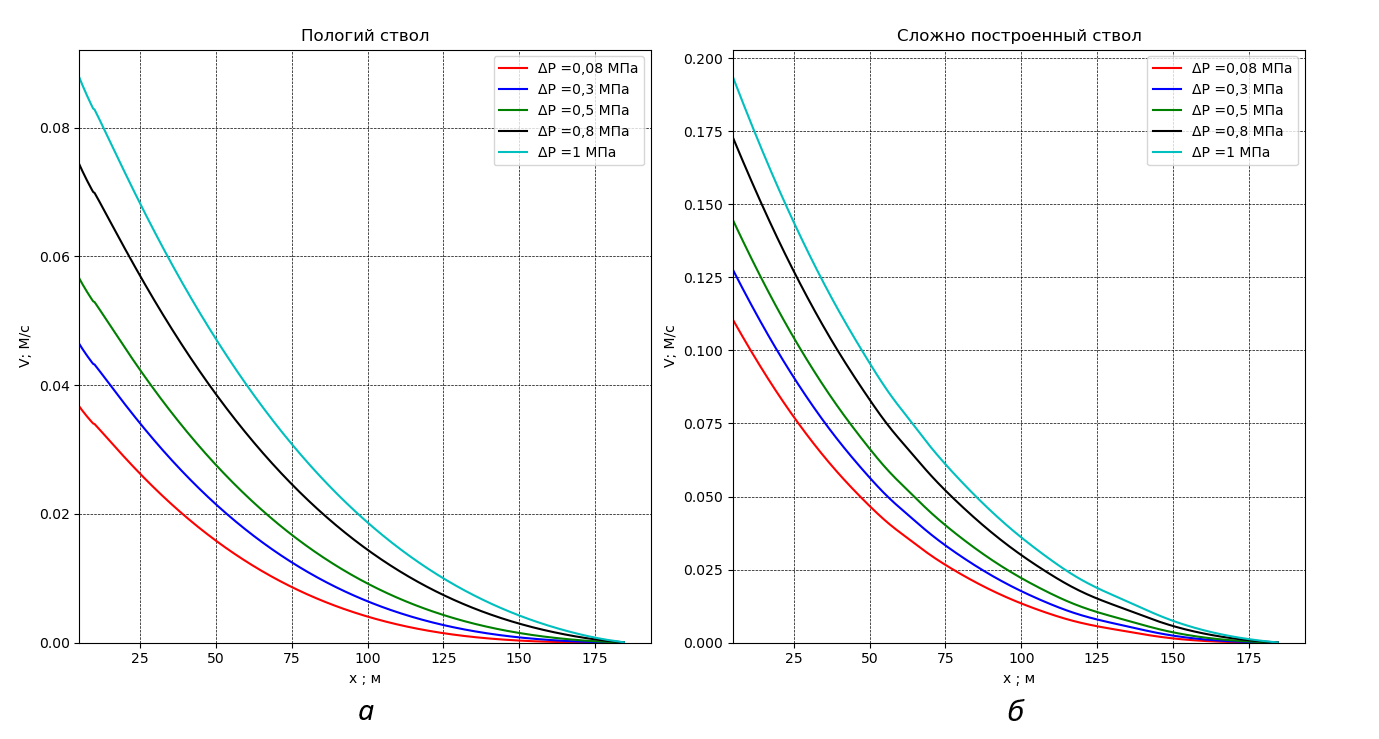
Рисунок 3 - Распределение скоростей потока по сегментам ствола вдоль пологой (а) и волнообразной (б) скважин
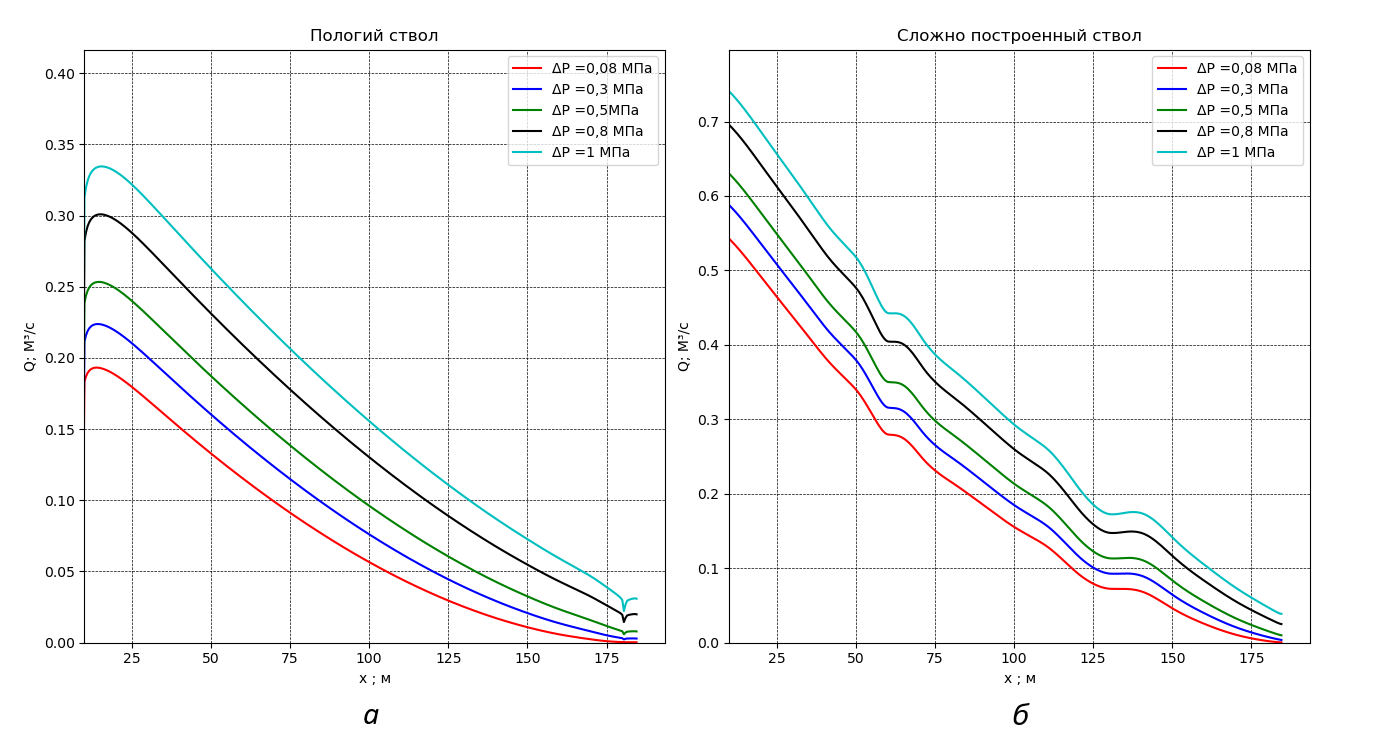
Рисунок 4 - Распределение притока вдоль ствола пологой (а) и волнообразной (б) скважин
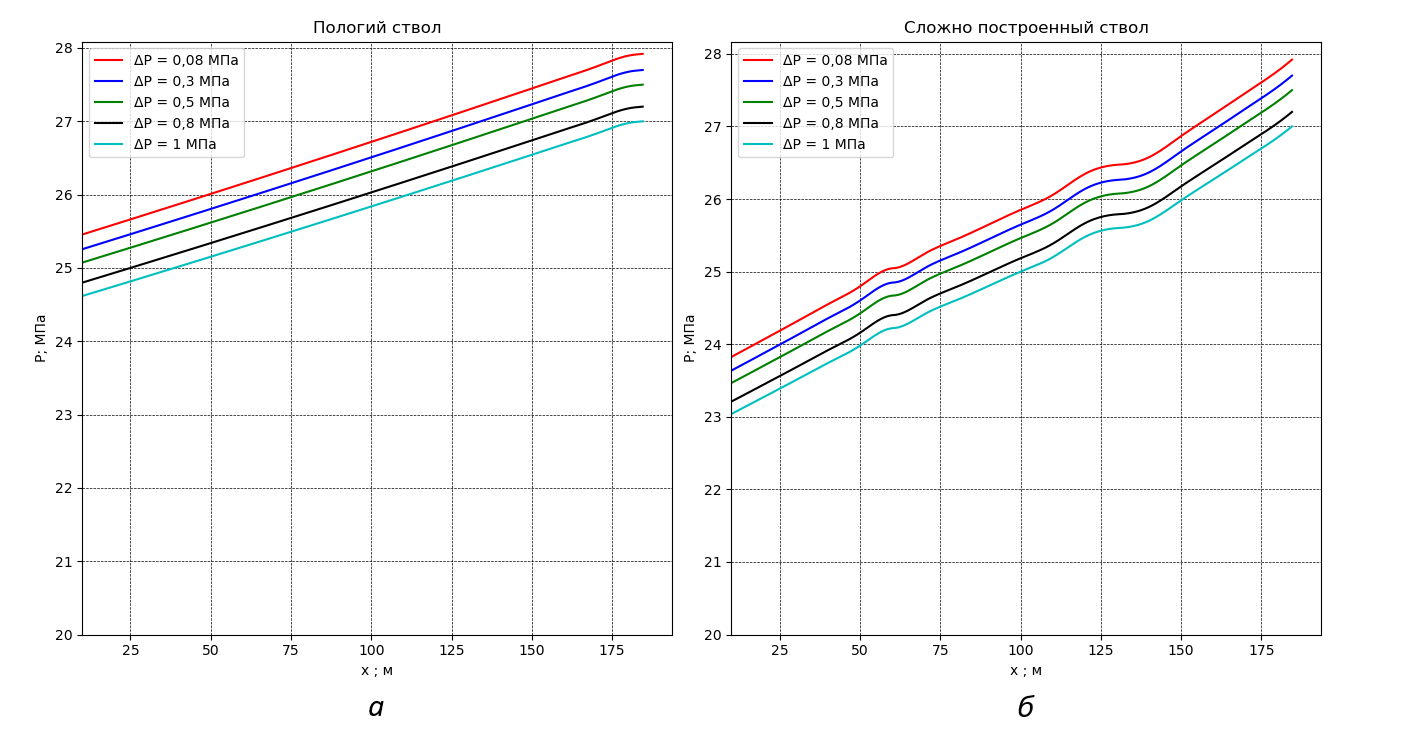
Рисунок 5 - Распределение давления по пологой (а) и волнообразной (б) скважине
4. Заключение
С использованием численно-аналитического решения были получены массовые дебиты сегментов в скважинах с пологим и волнообразным профилями в однородно-анизотропном газоносном пласте. Скважина волнообразного профиля позволяет достичь большей скорости потока, чем пологая скважина. Также по полученным результатам выявлено, что независимо от профиля ствола скважины в основном только работает начальный участок ствола.
Дальнейшие исследования будут включать в себя проведение факторного анализа для определения влияния параметров конструкции скважины и пластовой системы на производительности газовой скважины с горизонтальным окончанием.
