Прогнозирование перекрёстных помех в межсоединениях печатных плат с использованием искусственной нейронной сети
Прогнозирование перекрёстных помех в межсоединениях печатных плат с использованием искусственной нейронной сети
Аннотация
При разработке современных электронных средств на основе печатных плат из-за взаимного влияния межсоединений возникают перекрестные помехи. Если сигнал помехи превышает допустимые пороговые значения, то это может привести к ложному срабатыванию элемента, а тем самым и всей системы. Целью данной работы является реализация методики и прогнозирование параметров перекрестных помех в межсоединениях печатных плат на основе искусственной нейронной сети. Исследуются максимальная амплитуда и длительность помех на ближнем и дальнем конце межсоединения. Для исследования применялось искусственная нейронная сеть с полносвязной архитектурой с небольшим числом слоев и нейронов. Получено приемлемое расхождение результатов прогнозирования, не более 18% для всех параметров перекрестных помех на тестовой выборке. Приведены примеры прогнозирования максимальной амплитуды и длительность перекрестных помех.
1. Введение
При разработке конструктивов современных электронных средств, например, часто на основе печатных плат (ПП), если два или более сигнальных проводников на протяженных участках проводятся параллельно и близко друг к другу, то из-за взаимного влияния на входах пассивных цепей могут возникать побочные сигнальные напряжения (перекрёстные помехи)
, , . Это значит, что полезный сигнал в активной линии наводит в соседней (пассивной) линии сигнал помехи, который при превышении допустимых пороговых значений приводит к ложному срабатыванию элемента, а тем самым и всей системы. Особенно трудна оценка взаимного влияния в электрически длинных линиях. Поэтому для понимания механизмов возникновения перекрестных помех, их величин необходим анализ работы цифровых ПП. Данная задача также многократно усложняется, если при анализе необходимо учесть влияние множества активных проводников.Современные подходы исследования перекрёстных помех в ПП включают аналитическое и численное моделирование на этапе разработки электронных систем, что позволяет разработчикам тестировать решения до создания прототипов
, , , , , . Это способствует снижению затрат и времени разработки, однако сложность таких моделей не всегда позволяет точно учесть все физические процессы в реальных конструкциях ПП. Поэтому часто для решения задач со сложными нелинейными зависимостями рекомендуется использовать методы машинного обучения. Основное достоинство методов машинного обучения, в частности искусственных нейронных сетей (ИНС) это возможность учета явных и неявных зависимостей в больших наборах данных. Это достигается при достаточных обучающих данных и адекватном выборе, соответствующих сложности задачи, архитектуры и параметров ИНС. Таким образом, ИНС может выступать в пространстве обучения очень быстрым инструментом аппроксимации и, в какой-то мере, вне пространства обучения — инструментом экстраполяции.В научно-технической литературе
, , , , представлено множество исследований, где применение ИНС способно обрабатывать сложные нелинейные зависимости, характерные для многих реальных задач. Но в настоящее время авторами не обнаружены практико-ориентированные методики на основе ИНС для прогнозирования амплитудно-временных параметров перекрёстных помех в межсоединениях ПП.Целью данной работы является реализация практической методики и прогнозирование параметров перекрестных электромагнитных помех в межсоединениях ПП на основе искусственной нейронной сети. При этом в качестве параметров перекрестных помех рассматриваются ее максимальная амплитуда и длительность на ближнем и дальнем конце межсоединения.
2. Методы и принципы исследования
Объектом исследования в работе является фрагмент печатной платы с активным (А) и пассивным (П) межсоединением (рис. 1). Конструктивные (a, b, c, d) и электрофизические параметры (ℇ) данного фрагмента ПП соответствуют современному состоянию производства .
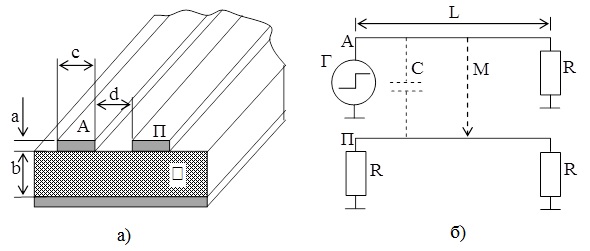
Рисунок 1 - Разрез фрагмента ПП (а) и схема подключения межсоединений (б)
Примечание: С – емкостное влияние; M – индуктивное влияние
На основании опыта использования ИНС для задач прогнозирования помех
, предлагается следующая практическая методика:1. Анализ входных параметров, существенно влияющих на величину перекрёстных помех (рис. 1).
2. Формирование набора данных с параметрами перекрестных помех в зависимости от входных факторов.
3. Выбор структуры и параметров ИНС для прогнозирования перекрёстных помех с приемлемой точностью на тестовых данных (не более 20% для задач помехоустойчивости ,
, , ). Количество нейронов во входном слое (l) соответствует количеству входных параметров. Количество нейронов в выходном слое (n) определяется количеством выходных (прогнозируемых) параметров. Другие параметры чаще всего выбираются опытным путем, например, на основе эмпирической формулы выбирается количество нейронов в скрытом слое (m) :m=sqrt(l+n)+q, где q – число от 1 до 10.
Изначально, для рассматриваемой задачи предложена нейронная сеть всего с тремя слоями: входным, скрытым и выходным. Выбор скорости обучения (learning rate) и значения функции потерь (training loss) осуществлялось опытным путем. Активационная функция всех нейронов сигмовидная.
4. Для обучения ИНС использовался алгоритм обратного распространения ошибки . При обучении функция потерь составляло от 0,07 до 0,3%. Скорость обучения варьировалось от 0,07 до 0,1. Для оценки качества решения задачи по тестовой выборке используется средняя абсолютная процентная ошибка (MAPE) .
5. Для входных и выходных данных использовалась нормализация данных обучения на основе минимаксного метода.
6. Этап обучения ИНС. Минимальное расхождение результатов при выбранной архитектуре ИНС достигается при значениях эпох от 501 до 1426.
7. Далее ИНС становится инструментом прогнозирования параметров перекрестных помех для произвольных значения входных факторов, в рамках установленного диапазона. Если прогнозируется превышение допустимых уровней перекрестных помех, то необходимо реализовать меры по снижению помех
, , , , , .3. Основные результаты и обсуждение
При выбранной архитектуре ИНС для тестовой выборки удалось добиться MAPE по рассматриваемым параметрам от 14 до 27%. Наибольшее значение ошибки (27%) получилось при тестировании по амплитуде FEXT. Это говорить о том, что зависимость данного параметра от входных факторов более сложная и простой архитектурой ИНС данную зависимость реализовать сложно. Для достижения приемлемой точности реализована четырёхслойная ИНС с двумя скрытыми слоями (рис. 2а). Приемлемое расхождение результатов при данной архитектуре ИНС достигается при 2003 эпохах (18%) (рис. 2б). Результаты обучения ИНС с использованием набора данных по максимальной амплитуде и длительности перекрестных помех на ближнем конце (NEXT) межсоединения представлены на рис. 3.

Рисунок 2 - Структура модернизированной ИНС (а) и результат обучения по амплитуде FEXT (б)
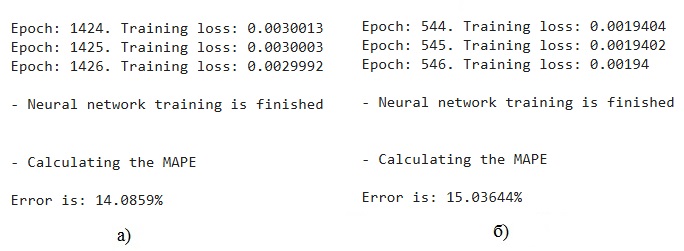
Рисунок 3 - Результат обучения ИНС по данным максимальной амплитуды (а) и длительности (б) помех NEXT
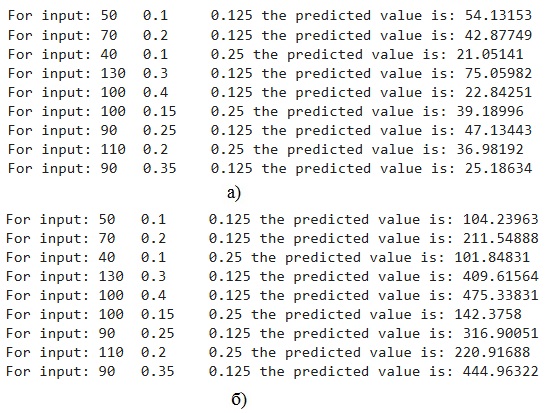
Рисунок 4 - Примеры прогнозирования амплитуды (а) и длительности (б) перекрёстных помех FEXT
Результаты исследования и прогнозирования перекрестных помех показывают, какие и насколько входные факторы влияют на ее амплитудные и временные параметры. При этом, в рассмотренном примере и диапазоне значений входных факторов, амплитуда NEXT составляет от 14 мВ до 60 мВ, FEXT от 3,5 мВ до 153 мВ. Длительность NEXT составляет от 270 до 1648 пс, FEXT от 89 до 548 пс.
4. Заключение
В статье предлагается практическая методика прогнозирования амплитуды и длительности перекрестных помех в ближнем и дальнем конце межсоединений ПП с использованием ИНС. Раскрываются все этапы реализации данной методики с учетом особенностей рассматриваемой задачи.
В качестве примера обучения ИНС используется существующий набор данных с параметрами перекрестных помех. Для тестовой выборки удалось добиться приемлемой средней абсолютной процентной ошибки для прогнозирования амплитуды и длительности перекрёстных помех с использованием достаточно простых архитектур ИНС (не более 18%). Наиболее сложную зависимость от входных параметров имеет максимальная амплитуда перекрёстной помехи на дальнем конце межсоединения. Приведены примеры прогнозирования всех рассмотренных параметров перекрёстных помех при произвольных входных параметрах в рамках рассматриваемого диапазона, с использованием обученной ИНС.
Для дальнейшего снижения ошибки обучения ИНС авторами рассматривается возможность существенного расширения количества обучающих данных, учет большего числа входных параметров, влияющих на перекрёстные помехи, и повышение сложности архитектуры нейронной сети.
Таким образом, на практике, предлагаемая методика может использоваться в качестве быстрого инструмента для прогнозирования параметров перекрёстных помех для множества различных длин и расстояний между межсоединениями при условии достаточно адекватного обучения ИНС на рассматриваемой конструкции ПП. В качестве перспектив использования данного типа инструмента можно обозначить задачи прогнозирования электромагнитных излучений, кондуктивных помех и др.
