СЕТЕВАЯ МОДЕЛЬ ФУНКЦИОНИРОВАНИЯ МНОГОНОМЕНКЛАТУРНОГО ПИЩЕВОГО ПРЕДПРИЯТИЯ

Остроух Е.Н.¹, Солопова О.Г.²

¹Доцент,  Донской государственный технический университет, кандидат технических наук, доцент (ДГТУ, г. Ростов-на-Дону),

²Доцент, Ростовский государственный экономический университет, кандидат технических наук, доцент (РГЭУ, г. Ростов-на-Дону)

СЕТЕВАЯ МОДЕЛЬ ФУНКЦИОНИРОВАНИЯ МНОГОНОМЕНКЛАТУРНОГО ПИЩЕВОГО ПРЕДПРИЯТИЯ

Аннотация

В статье рассмотрена методика использования сетевых моделей, описывающих работу предприятий пищевой промышленности, с большой номенклатурой продукции, предложен алгоритм, оптимизирующий стратегию и объемы выпускаемой продукции с учетом дефицита входных ресурсов. 

Ключевые слова: технологический процесс, сетевая модель, максимальный поток

Ostrouh E.N.¹, Solopova O.G.²

¹Professor  of  department, Don state technical University, candidate of technical Siences ( DSTU, Rostov on Don),

² Professor  of  department, Rostov state economic University, candidate of technical Siences  (RSEU, Rostov on Don)

NETWORK MODEL OF FUNCTIONING OF THE WIDE NOMENCLATURE OF FOOD ENTERPRISES

Abstract

In this paper reviewed the technique of using network models, describing work of enterprises of  food  industry whis a wide range of products, proposed  an algorithm for optimizing strategy and volumes of manufactured products with this, to a scarcity of  resources  

        Keywords: technological process, network model, maximum flow

        Технологический процесс изготовления пищевой  продукции можно интерпретировать некоторым простым ориентированным графом (без петель и кратных ребер) G(X,E), где E={e₁₁,e₁₂,…,e_nm}- дуги; дуга e_ij интерпретирует

j-й технологический процесс технологии T_i. Вершины X={x₁,x₂,…,x_k} интер-претируют факт начала и окончания технологического процесса j технологии T_i. Каждой дуге (e_ij) графа  G(X,E) сопоставляется вес c_ij- стоимость процесса j технологии i (затраты и издержки). На пропускные способности дуги (e_ij) наложены ограничения сверху и снизу: r_ijx_ij R_ij, где x_ij-поток продукта по j-му процессу технологии T_i. Ограничение R_ij получается, исходя из ограничений на максимальную производительность (мощность) оборудования и рыночный спрос на данную продукцию; ограничение r_ij связано с договорными обязательствами и обязательствами по госпоставкам. В самом общем случае граф  G(X,E) –многопродуктовая, многополюсная сеть, в которой необходимо найти максимальный поток минимальной стоимости. Полюсы представляют собой один источник (вход) S, куда производится поставка исходного сырья (например, молока, если имеем молочный комбинат) и n стоков (выходов) по количеству номенклатуры выпускаемой продукции.                                                                               

        Итак, имеем следующую задачу:

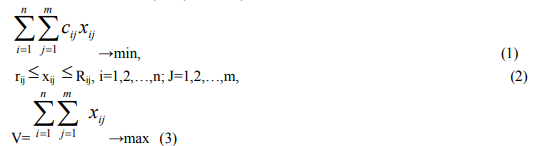
Оптимальное решение задачи (1)-(3) позволит решить задачу о нахождении максимального потока в сети (максимальной загрузки оборудования), оптимальной с точки зрения номенклатуры выпускаемой продукции, с учетом ограничений, связанных с обязательными поставками готовой продукции, спросом на эту продукцию и мощностью имеющегося на комбинате оборудования.

Граф G(X,E) представим суммой двух графов: G(X,E)= G₁(X^I,E^I)+ G₂(X^II,E^II), где G₁(X^I,E^I)-подграф, интерпретирующий набор общих технологий (например, процесс нормализации в молочной промышленности) для всей номенклатуры изделий; E^I-множество дуг, интерпретирующих эти общие технологии, а X^I-соответственно факты начала и окончания этих процессов. Вообще говоря, граф G₁(X^I,E^I) представляет собой сеть с одним источником (сырье) и одним стоком – полуфабрикат для дальнейшей переработки в готовую продукцию. На этом этапе (интерпретированном графом G₁(X^I,E^I)) решаем классическую задачу о максимальном потоке: находим максимальное количество полуфабриката V^I, получаемого из сырья (молока) объема V. При этом используем один из алгоритмов задачи о максимальном потоке, описанный в [1].

Граф G₂(X^II,E^II) интерпретирует технологии (процессы) изготовления пищевых продуктов, здесь X^II и E^II соответственно вершины и ребра, связанные с особенностью каждой технологии T_k изготовления готовой продукции. Имеет один вход: S₁- на который подается полуфабрикат, затем получается система n параллельных  подграфов, с общим входом S₁, интерпретирующих каждую из технологий T_k, k=1,2,…,n, т.е., имеем сеть с одним входом и n выходами (стоками). Для каждого такого подграфа решаем задачу 1)-(3).

На этом этапе учитываем стоимость готовой продукции, т.е., считаем, что задан вектор цен готовой продукции Ц=(ц₁,ц₂,…,ц_n).

Опишем алгоритм решения задачи для графа G₂(X^II,E^II).

Шаг 1. По всем дугам параллельных подграфов  графа G₂(X^II,E^II) пропускаем начальные потоки, равные заданным значениям r_ij.

Шаг 2. Упорядочим вектор Ц по убыванию весов.

Шаг 3. Выбираем первую компоненту упорядоченного вектора Ц^I.

Шаг 4. Решаем задачу о нахождении максимального потока для подграфа, соответствующего этой технологии.

Шаг 5. Продолжаем этот процесс, пока не пройдем все параллельные подграфы, т.е., не пройдем все технологии до конца или процесс остановится при условии полного использования ресурса V^I.                                                                                                     

Шаг 6. Конец работы алгоритма.

Замечание. Если по окончании алгоритма расходуется не весь ресурс полуфабриката V^I, то необходимо принять меры по хранению полуфабриката или, возвращаясь к графу G₁(X^I,E^I) скорректировать объем исходного сырья V, т.е., уменьшить, например, поставки молока, если имеем молкомбинат, либо перепродать его партнерам.

Предложенный алгоритм позволяет найти оптимальное количество готового продукта, которое обеспечит предприятию максимальную прибыль, с учетом гарантированных поставок по договорам и госзаказу. Оценка алгоритма составляет О(m²), где m- число дуг исходного графа G.