ДЕТЕРМИНИСТИЧЕСКИЕ ФРАКТАЛЫ НА ОСНОВЕ ИТЕРАЦИОННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ТОЧЕК В 2D ПРОСТРАНСТВЕ

Иванов В.В.

Кандидат химических наук, доцент, Южно-Российский государственный технический университет (Новочеркасский политехнический институт)

ДЕТЕРМИНИСТИЧЕСКИЕ ФРАКТАЛЫ НА ОСНОВЕ ИТЕРАЦИОННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ТОЧЕК В 2D ПРОСТРАНСТВЕ

Аннотация

Обсуждается возможность формирования детерминистических фрактальных структур на основе итерационной последовательности точек в 2D пространстве.

Ключевые слова: итерационная последовательность, детерминистическая фрактальная структура.

Ivanov V.V.

PhD in Chemistry, associate professor, South-Russian state Еngineering University (Novocherkassk Polytechnic Institute)

DETERMINISTIC FRACTALS BASED ON ITERATIVE SUCCESSIVE OF POINTS IN 2D SPACE

Abstract

The possibility of the formation of deterministic fractal structure based on iterative successive of points in 2D space was discussed.

Keywords: iterative successive, deterministic fractal structure.

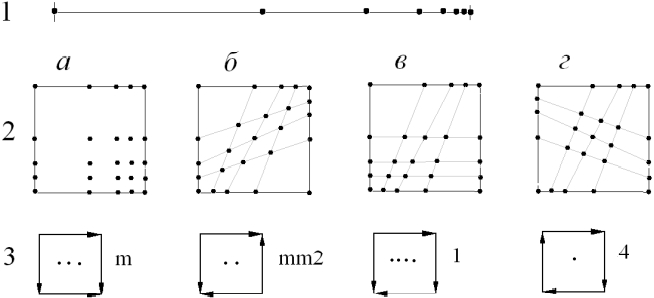
Ранее были разработаны основы модулярного дизайна детерминистических фрактальных структур (в т.ч. и точечных) в 2D пространстве [1-12]. В частности было установлено, что начиная со 2-го поколения все предфракталы фрактала на основе итерационной последовательности точек IC(1/2), заданной на единичном интервале [0…1] 1D пространства, являются асимметричными [11] (рис.1, фрагмент 1). В связи с этим возможные варианты реализации двух асимметричных фракталов IC(1/2) в квадратной ячейке 2D пространства будут отличаться как по конфигурации точек и симметрии (рис.1, фрагменты 2 и 3), так и по своим структурным кодам, обладая одинаковой локальной размерностью (табл.1): Dim IC² = 2 Dim (GenIC(1/2)) = 1,000.

Рис.1 - Предфрактал 6-го поколения итерационной последовательности точек IC(1/2) на единичном интервале 1D пространства (1), возможные на ее основе предфракталы 3-го поколения в квадратной ячейке 2D пространства (2) и их соответствующие маркированные графические изображения с указанием точечной группы симметрии G²₀ (3).

     Таблица 1 - Коды, симметрия и размерность детерминистических фракталов на основе итерационной последовательности                                  точек в 2D пространстве.

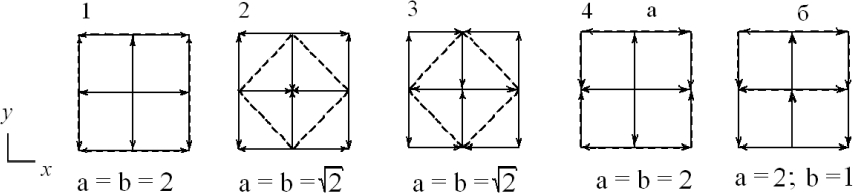
При формировании детерминистической фрактальной структуры на квадратной сетке путем вложения в ее ячейки определенных фракталов будем принимать во внимание только самые симметричные структуры с минимальными периодами идентичности в двух независимых направлениях, т.е с минимальными параметрами элементарной ячейки. Изображения некоторых высоко симметричных детерминистических структур представлены на рис.2.

 

Рис.2 - Схематические изображения фрагментов детерминистических фрактальных точечных структур на основе итерационной последовательности из фракталов с кодами 0121 (1), 0202 (2), 1111 (3) и 0112 (4, варианты а,б) на квадратной сетке, симметрия G²₂ 2D структур и соответствующие параметры элементарной ячейки (в единицах параметра квадратной ячейки 2D пространства).

Структуры полученных детерминистических фракталов описываются тремя плоскими группами, принадлежащими к двум двумерным группам Браве: квадратной (p4mm) и примитивной ромбической (pmm2, pm). Отметим, что асимметричный точечный фрактал с кодом 0112 (G²₀= 1) может быть использован для получения невырожденных модулярных детерминистических фрактальных структур - политипов. В данном случае словосочетание «невырожденная модулярная структура» означает возможность получения на основе одной структуры некоторого множества структур, состоящих из одних и тех же модулей- фракталов, но отличающихся от исходной структуры и друг от друга ориентационным и позиционным упорядочением в 2D пространстве. Пример двух первых структур из политипного ряда приведен на рис. 2 (фрагменты 4а и 4б). Следует также отметить, что глобальная размерность всех полученных выше детерминистических фрактальных структур совпадает с размерностью пространства и равна 2. Некоторые из полученных результатов использованы при объяснении эффекта синергизма антифрикционных свойств компонентов композитов [13-18].

Литература

1. Иванов В.В., Таланов В.М. Принципы модулярного строения регулярных фрактальных структур // Успехи соврем. естествознания, - №3. – С.56-57.
2. Иванов В.В., Демьян В.В., Таланов В.М. Информация и структура в наномире: модулярный дизайн фрактальных структур в двумерном пространстве // Междунар. журн. эксп. образования, - №11. - С.153-155.
3. Иванов В.В., Таланов В.М., Гусаров В.В. Информация и структура в наномире: модулярный дизайн двумерных наноструктур и фрактальных решеток // Наносистемы: Физика, Химия, Математика, - Т.2. - № 3. - С.121-134.
4. Иванов В.В., Таланов В.М. Разбиение и структурирование пространства, описание процесса формирования модульного кристалла // Успехи соврем. естествознания, - №8. – С.75-77.
5. Иванов В.В., Таланов В.М. Разбиение структурированного 3D пространства на модулярные ячейки и моделирование невырожденных модулярных структур // Успехи соврем. естествознания, - №10. – С.78-80.
6. Иванов В.В., Таланов В.М. Формирование структурного модуля для модулярного дизайна в 3D пространстве // Успехи соврем. естествознания, 2012. - №9. – С.74-77.
7. Иванов В.В., Демьян В.В., Таланов В.М. Эволюционная модель формирования и анализ детерминистических фрактальных структур // Успехи соврем. естествознания, 2012. - №4. – С.230-232.
8. Иванов В.В. Общая характеристика возможных гибридных мономодулярных фрактальных структур// Соврем. наукоемкие технологии. 2013.- №.5. – С.29-31.
9. Иванов В.В. Формирование фрактальных структур на основе итерационной последовательности и канторова множества точек с заданными характеристиками в 1D пространстве // Успехи соврем. естествознания, 2013. - №8. – С.136-137.
10. Иванов В.В. Описание и классификация точечных мономодулярных фрактальных структур // Успехи соврем. естествознания, - №8. – С.134-135.
11. Иванов В.В. Анализ возможности получения новых точечных и квазиточечных фрактальных структур на основе итерационной последовательности и канторова множества // Успехи соврем. естествознания, - №8. – С.129-130.
12. Иванов В.В., Таланов В.М. Конструирование фрактальных наноструктур на основе сеток Кеплера-Шубникова // Кристаллография, – Т.58. - № 3. - С. 370–379.
13. Иванов В.В., Щербаков И.Н., Иванов А.В., Башкиров О.М. Анализ синергического эффекта в композиционных никель- фосфорных покрытиях // Изв. вузов. Сев-Кавк. регион. Техн. науки, - №4. - С.62-64.
14. Ivanov V.V., Balakai I., Ivanov A.V., Arzumanova A.V. Synergism in composite electrolytic nickel-boron-fluoroplastic coatings// Rus. J. Appl. Chem., 2006. - Т.79. - №4. - С.610-613.
15. Ivanov V.V., Balakai I., Kurnakova N.Yu. et al. Synergetic effect in nickel-teflon composite electrolytic coatings // Rus. J. Appl. Chem., 2008. - Т.81. - № 12. - С.2169-2171.
16. Balakai I., Ivanov V.V., Balakai I.V., Arzumanova A.V. Analysis of the phase disorder in electroplated nickel-boron coatings // Rus. J. Appl. Chem., 2009. - Т.82. - №.5. - С.851-856.
17. Щербаков И.Н., Иванов В.В. Анализ возможных модификаторов для получения композиционных Ni-P покрытий с антифрикционными свойствами // Изв. вузов. Сев.-Кавк. регион. Техн. науки. №5. С.47-50.
18. Иванов В.В., Щербаков И.Н. Моделирование антифрикционных свойств композиционных покрытий с учетом вероятных конфигураций межфазных границ // Изв. вузов. Сев.-Кавк. регион. Техн. науки. №3. С.54-56.