«Стрела времени» – фантом столетней давности

This paper is devoted to the problem of relation between reversible and irreversible processes in physics. The problem is posed in connection with the second law of thermodynamics: from the laws of mechanics it follows that entropy is constant, whereas the second law of thermodynamics requires the entropy to increase. This problem (the significance of which goes far beyond physics) is discussed in a great number of papers (for example, in many books of Nobel prize-winner I. Prigogine

As a result, quasi-philosophical arguments about the “arrow of time”

Sharing Martynov’s opinion, we, in our turn, formulate the following statements:

The discussed contradiction exists in our descriptions of nature, but not in nature itself. Nature is a single entity that cannot possess contradictory features. Correspondingly, if we have contradictory descriptions of nature, at least one of the descriptions has a logical error.

Therefore, in an attempt to solve the posed problem, one should focus on a thorough logical analysis of the relationship between the basics of mechanics and thermodynamics in order to find the hidden logical mistake that leads to the seeming contradiction, rather than try to apply methods of mathematical physics.

In our opinion, the logical mistake here is that the second principle of thermodynamics is given the status of law. A law is a statement, which is true always, and everywhere, under any conditions. The second principle of thermodynamics, however, was deduced on potential grounds, and in any system there is a probability that it will be violated. The contradiction between dynamics and thermodynamics is a consequence of the unrightfully given status of the second principle (which is probabilistic in essence), and because of this status certain dynamically possible conditions are.

This prohibition becomes an absolute fact of adopting the status of low for probabilistic. This can be illustrated by the following situation: all inhabitants of the Earth participate in a lottery with a single win. The probability of a win is so low that everyone takes it to be nil. Thus, a “contradiction” may arise between the statements that no one has a chance to win and somebody is sure to win.

The explanations statements formulate above are discussed below.

An irreversible process in thermodynamics is a process that increases entropy: the initial conditions cannot be regained. In a great number of papers, The Second Principle is treated as a universal law applicable to data distribution of any nature. According to this approach, Information values are calculated by distribution of certain parameters and then interpretation is implemented in terms of increase/decrease of ordering, etc.

Let us consider a simple computer model of a cell automate (fig. 1), which is commonly used to illustrate statistic regularities of thermodynamic processes. We shall model in this case.

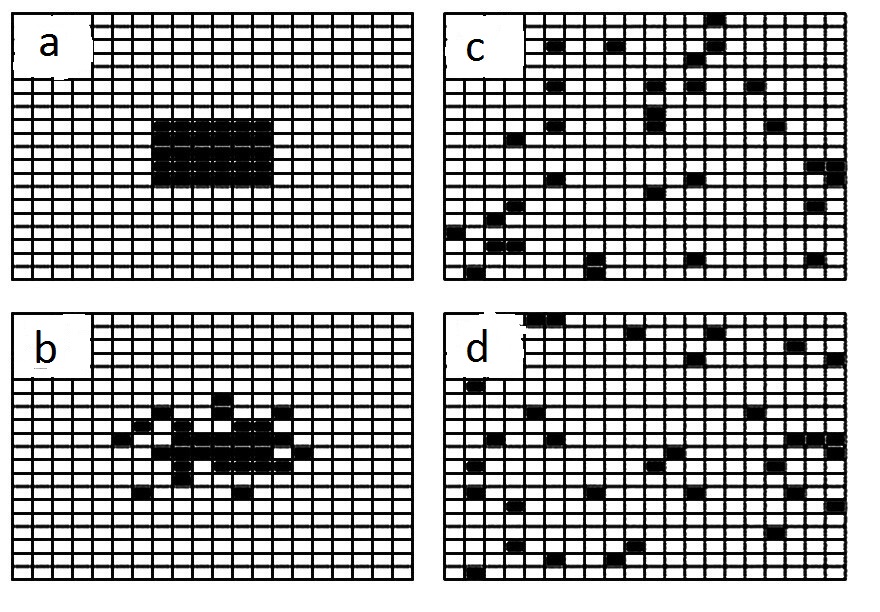
Figure 1 - Computer simulation of diffusion:

a-d – stages of the process

DOI:10.23670/IRJ.2023.133.17.1

The beginning of the process is shown in Fig 1(a): on a microscopic level (in the model this is the level of individual cells; or molecules, Brownian particles, etc. in nature) we have a distribution of parameters (X and non-X) in space. The general pattern of a drop of material X in the environment   is seen only macroscopically. Let us now set the algorithm for the process to develop: with every temporal quantum, a randomly chosen particle moves to an adjacent empty cell (if any).   In due course we will have the patterns shown in Fig. 1(b), 1(c) and so on. This agrees fairly well with the real processes: a drop of ink would dissolve in water, and gas molecules would tend to fill up the entire volume.

Note what the difference between the systems shown in Fig 1(a) and Fig (b - d) exists only in a macroscopic level; microscopically, X is distributed in a different way, no more. The distribution in 1(a) does not differ basically from the distribution in 1(d), and if we follow the path a – b – c – d in opposite direction, we shall the 1(a) distribution again. The state 1(a) is privileged only in terms of a macroscopic description, which, in turn, exists only in sensual perception of an observer, whereas nature consists of atoms and energetic fields. The transition from 1(b) to 1(c) or 1(d) occurs as rarely as the transition from 1(b) to 1(a), but a macroscopic observer does not fix the difference between 1(b – d) (and between a large number of other states of a system). All these distributions are called by a common name “mixture” or “chaos”, and opposed to “order” (1(a)).  Having singled out in our numerical experiment, conditionally speaking, one (1a) of 10n equiprobable states, we will certainly see, in accordance with the probability theory, that this unique state is replaced by some other one and does not reappear for a very long time. In the end, it will nevertheless arise: within 10n time intervals. In the theory of thermal processes, this extremely low probability can, of course, be neglected. At this level of description, thermodynamics is extremely efficient, allowing huge dynamic descriptions to be replaced by a few macro variables. However, when analyzing the relationship between dynamics and thermodynamics at the level of individual particles, approximated by sets with a finite number of elements, even a vanishing small probability of the system returning to its original state is of fundamental importance, in the sense that the mystical ban on some states of the dynamic system disappears, from the point of view of thermodynamics having less entropy. In probabilistic terms, the statement of the 2nd law of thermodynamics about the steady increase in entropy loses its mystery and sounds almost like a tautology: more probable processes occur with a greater probability. In fact, within the framework of mechanics, irreversible processes can be detected: thus, following the pattern of the “arrow of time” one can introduce an “arrow of space” based on the fact that gravity on the Earth is always directed towards its center (after all, no one considers the fact that stones roll spontaneously only downhill as a violation of the symmetry of the equations of mechanics!).

Thus, the "problem" of matching dynamics and thermodynamics turns out to be a pseudo-problem based on the violation of the logical law of identity. The solution to the “problem” is so simple that it is difficult for the authors to imagine that no one has thought of it for a century and a half; however, we do not know of publications where the resolution of this “problem” before 1997 (the date of our first publication on the topic under discussion