АВТОМАТИЗАЦИЯ ПРОЕКТИРОВАНИЯ СЕРПАНТИН

АВТОМАТИЗАЦИЯ ПРОЕКТИРОВАНИЯ СЕРПАНТИН

Научная статья

Лопашук В.В.¹, ^*, Лопашук А.В.² , Лопашук С.В.³

¹ ORCID: 0000-0003-2005-6055;

² ORCID: 0000-0002-7823-3889;

³ ORCID: 0000-0002-5732-6242;

^{1, 2} Тихоокеанский государственный университет, Хабаровск, Россия;

³ ООО «Прогресс-ДВ», Хабаровск, Россия

^* Корреспондирующий автор (VLopashuk[at]27pro.ru)

Аннотация

В современных системах автоматизированного проектирования автомобильных дорог отсутствует возможность проектирования классических серпантин. Процесс проектирования сводится к конструированию комбинаций сложных закруглений, по форме напоминающих серпантину. В настоящей статье использован единый метод расчета и проектирования серпантин, предложенный авторами и разработан алгоритм автоматизации проектирования любых серпантин. В качестве исходных данных используют координаты вершин углов поворота трассы, центра основного закругления и параметры серпантины (радиусы круговых кривых, длины клотоид и прямых вставок). Смещая центр основного закругления серпантины, разработанный авторами алгоритм расчета, позволяет менять не только форму серпантины (вытянутая, нормальная или сжатая), но и вид (I рода, полусерпантина, II рода). В частном случае серпантина может превратиться в обычную, вписанную круговую кривую. В статье приведен пример расчета серпантины. Внедрение в САПР АД предлагаемого метода расчета и алгоритма его реализации существенно упростит проектирование серпантин на автомобильных дорогах, повысит качество принимаемых проектных решений.

Ключевые слова: серпантина, клотоида, закругление, радиус, координаты, полигональное трассирование.

SERPENTINE DESIGN AUTOMATION

Research article

Lopashuk V.V.¹, ^*, Lopashuk A.V.² , Lopashuk S.V.³

¹ ORCID: 0000-0003-2005-6055;

² ORCID: 0000-0002-7823-3889;

³ ORCID: 0000-0002-5732-6242;

^{1, 2} Pacific National University, Khabarovsk, Russia;

³ Progress-DV" LLC, Khabarovsk, Russia

^* Corresponding author (VLopashuk[at]27pro.ru)

Abstract

In modern systems of computer-aided design of highways, there is no possibility of designing classical serpentin. The design process comes down to the construction of combinations of complex turns that resemble a serpentin in shape. This article uses a unified method for calculating and designing serpentin, proposed by the authors; and an algorithm for automating the design of any serpentin has been developed. The coordinates of the vertices of the road rotation angles, the center of the main turn and the parameters of the serpentin (radii of circular curves, lengths of clothoids and straight inserts) are used as initial data. By shifting the center of the main turn of the serpentin, the calculation algorithm developed by the authors allows changing not only the shape of the serpentin (elongated, normal or compressed), but also the type (I genus, half-serpentine, II genus). In a particular case, the serpentin can turn into an ordinary, inscribed circular curve. The article provides an example of calculating the serpentin. The introduction of the proposed calculation method and the algorithm of its implementation into CAD AD will significantly simplify the design of serpentin on highways, improve the quality of design decisions.

Keywords: serpentin, clothoid, curving, radius, coordinates, polygonal tracing.

Введение

При проектировании дорог в горных условиях, уменьшая продольный уклон, проектировщик вынужден удлинять трассу, прокладывая ее под углом к горизонталям, устраивать большие углы поворота трассы, а вершины этих углов описывать сложными закруглениями – серпантинами, состоящими в общем виде из шести клотоид трех круговых и двух прямых вставок.

Расчетами серпантин занимались многие отечественные ученые. Небольшую известность получила книга Н.А. Митина [1], выдержавшая два издания. В своих исследованиях Н.А. Митин впервые сформулировал понятие общего метода расчета серпантин, однако при этом рассматривал различные расчетные схемы: серпантины I и II рода; полусерпантины; вытянутые; сжатые; с левым и правым положением центра основного закругления. Каждая схема серпантины сопровождалась своими зависимостями и формулами, что исключает их универсальность. Основной недостаток метода Н.А. Митина заключается в отсутствие окончательного решения при расчете величин углов вспомогательных закруглений сложных серпантин. Предложенные им уравнения являются нелинейными, а их решение – примерным.

 Точный расчёт серпантины описан профессором Г.Д. Дубелиром [2]. Им рассмотрен расчет серпантины I рода. Недостаток метода Г.Д. Дубелира заключался в сложности расчетной схемы, наличии нескольких систем координат и как следствие, в универсальности расчета. Кроме этого вспомогательные закругления должны быть круговыми кривыми, что значительно сужает область использования этого метода.

Широкое применение получил метод П.И. Седельникова [3], в своей работе он описал точный метод расчета простой серпантины, когда центр основного закругления находится в вершине угла поворота трассы, а вспомогательные закругления симметричные. При смещении центра основного закругления с вершины угла, расчет значительно усложняется, расчетные зависимости вырождаются в нелинейные уравнения, но автор продолжал неправомерно использовать уравнения, полученные для простых серпантин.

Метод П.И. Седельникова описан во многих публикациях и учебниках [4], [5], [6] в которых либо детально не рассматривали расчет сложных серпантин, либо предлагали алгоритмы последующей корректировки исходных данных, для получения согласованных решений, используя полученные результаты расчета [7].

Анализируя существующую практику расчета и проектирования серпантины как единого сложного закругления можно констатировать, что точные решения известны только для частного случая, когда центр основного закругления расположен в вершине угла поворота, а вспомогательные закругления симметричные. Расчет серпантины профессора Г.Д. Дубелира хотя и точный, но имеет ограничения по типам вспомогательных закруглений и сложен в применении. Во всех остальных случаях решения либо приближенные, либо требуют корректировки исходных данных.

Авторами настоящей статьи предложена общая расчётная схемы серпантины и получены нелинейные (трансцендентные) уравнения нахождения углов поворота вспомогательных закруглений. Используя методы тригонометрии решены нелинейные уравнении и разработан алгоритм расчета серпантин любого вида и рода [8]. Полученное решение нельзя признать универсальным: в расчетной схеме используют локальную систему координат; положение основной кривой должно быть справа; положение центра основного закругления указывают в радиальной системе координат. Указанные требования не позволяют без доработки, использовать предложенный метод расчета в САПР АД.

Особо отметим, что при проектировании серпантин следует стремиться не только к выполнению корректных расчетов, но и к повышению качества серпантины и достижению минимальных объемов строительных работ при определенных качествах. Качество серпантины определяется скоростью, с которой расчетный автомобиль будет безопасно проходить по ней. Указанные требования, предъявляемые к серпантинам, могут быть достигнуты только при многовариантном проектировании с применением САПР АД, визуализации и анализе проектных решений.

В современных программных продуктах по автоматизированному проектированию автомобильных дорог нет процедуры проектирования серпантины. Кроме этого многие исследователи вообще не рассматривают серпантину как единое сложное закругление, подчиняющие взаимосвязанным законам конфигурирования, когда изменение какого-либо параметра серпантины может привести к изменению всех её элементов. Проектировщик вынужден «собирать» серпантину из отдельных, не связанных между собой, закруглений. Такой подход к проектированию серпантинных трасс является сложным и не позволяет качественно оптимизировать проектные решения.

Цель и задачи исследования

Исходя из изложенного, целю настоящего исследования является: обеспечение качества проектирования серпантин с применением современных САПР АД.

Задачами исследования являются:

1. Усовершенствование общего метода расчета серпантин, обеспечивающего возможность применения его в современных программных продуктах.
2. Разработка алгоритмов автоматизации расчета и проектирования серпантин.
3. Визуализация проектирования серпантин в САПР АД.

 

Основные результаты

Современные технологии автоматизированного проектирования предполагают использование цифровых моделей местности (ЦММ) [5], [9], [10]. Цифровая модель автомобильной дороги при полигональном трассировании представляет собой массив координат вершин углов поворота трассы (рис.1) и массив параметров закруглений. Массив координат:, где  ; точка  – начало трассы (НТ); точка – конец трассы (КТ); точки  углы поворота.

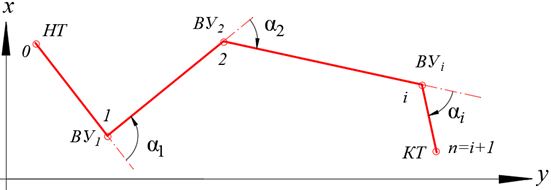
Рис. 1 – Ломаный магистральный ход

Структура массива параметров закруглений зависит от вида закругления, которые могут быть вписываемые во внутренние углы (рис.2) и описывающие внешние углы (рис.3). Последние закругления называют серпантинами.

Параметрами вписываемого закругления общего вида (рис. 2) являются: R – радиус круговой кривой; L₁, L₂ – длина переходных кривых (клотоид) в начале и в конце закругления.

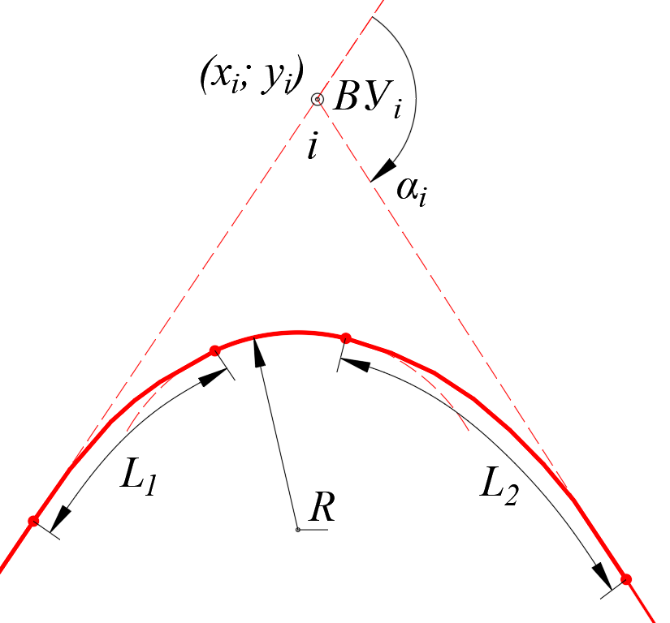
Рис. 2 – Параметры закругления, вписанного во внутренний угол

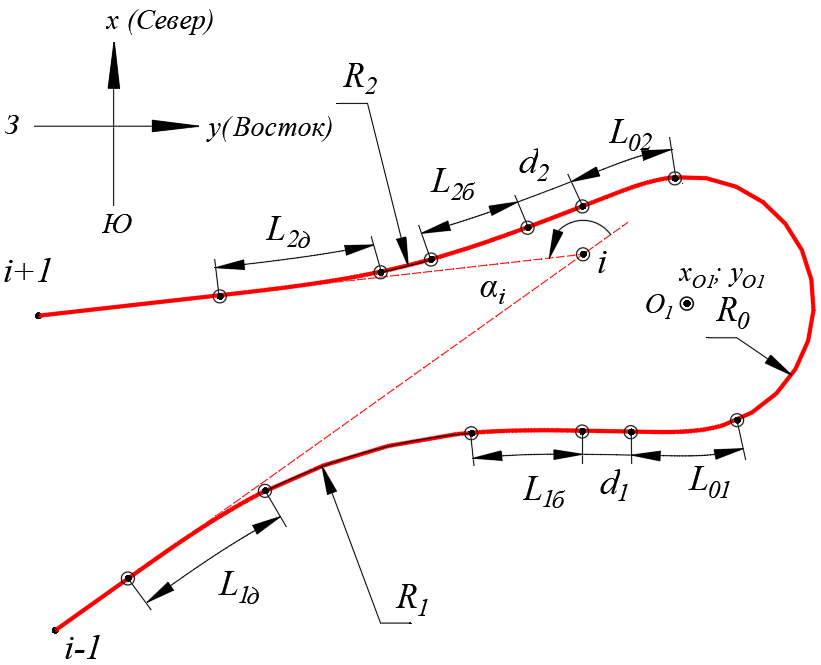
Рис. 3 – Параметры серпантины

Описываемое закругление, серпантина общего вида, (рис.3) состоит из основной кривой, двух вспомогательных закруглений и двух прямых вставок между ними. Поэтому параметрами серпантины являются: R₀ – радиус круговой кривой основного закругления; L₀₁, L₀₂ – длины переходных кривых в начале и в конце основного закругления; R₁, R₂ – радиусы вспомогательных закруглений; L_1д, L_2д – длины переходных кривых вспомогательных закруглений, расположенных дальше (д) от основного; L_1б, L_2б – длины переходных кривых вспомогательных закруглений, расположенных ближе (б) к основному; d₁, d₂ – длины прямых вставок; x_o1,y_o1 – координаты центра основного закругления.

При известных координатах магистрального хода и параметрах закруглений рассчитывают элементы плана трассы и составляют ведомость углов поворота [11]. Для этого вычисляют дирекционные углы направлений, угол поворота трассы и его направление.

Алгоритмизация проектирования серпантин

Дирекционные углы направлений вычисляют по приращениям координат между вершинами ломаного магистрального хода:

Для дальнейших рассуждений, упростим обозначение приращений координат, убрав указание на номера точек магистрального хода (рис.4).

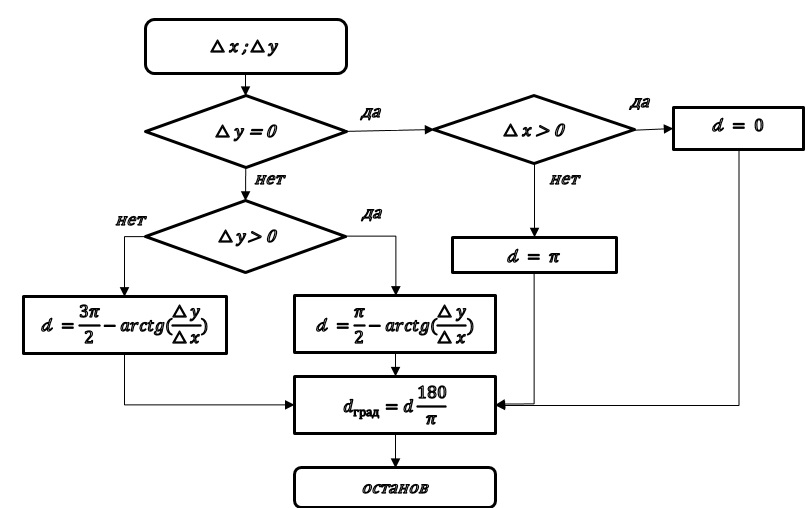
Рис. 4 – Алгоритм вычисления дирекционных углов направлений

Угол поворота трассы – это угол между продолжением предыдущего направления прямолинейного участка трассы и последующим её направлением. Углы поворота разделяются на левые и правые. Такое разделение, с одной стороны наглядное, а с другой – позволяет учитывать знак угла в последующих расчетах. Направление поворота трассы обозначим через (n) которое принимает значение (-1) при повороте трассы на лево и (+1) при повороте трассы направо. Углы поворота вычисляют через дирекционные углы (рис.5).

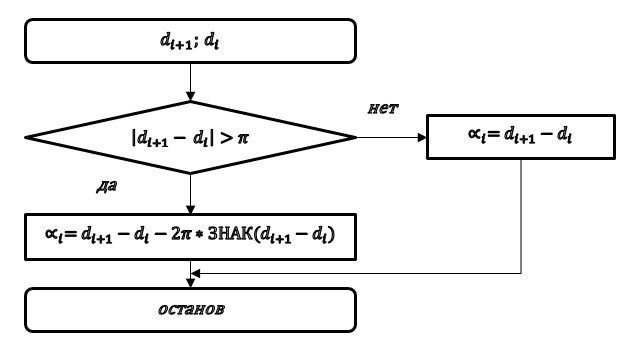
Рис. 5 – Алгоритм вычисления угла поворота трассы

Визуальное проектирование вписываемых закруглений и серпантин с применением специальных программ может существенно отличаются.

Вписываемые закругления, при заданном положении магистрального хода (рис.6), проектируют в следующей последовательности:

• назначают параметры закругления (R, L₁, L₂);
• проверяют условие размещения клотоид в пределах закругления [6]:

• визуально оценивают качество проектных решений и при необходимости меняют параметры или положение вершины угла.

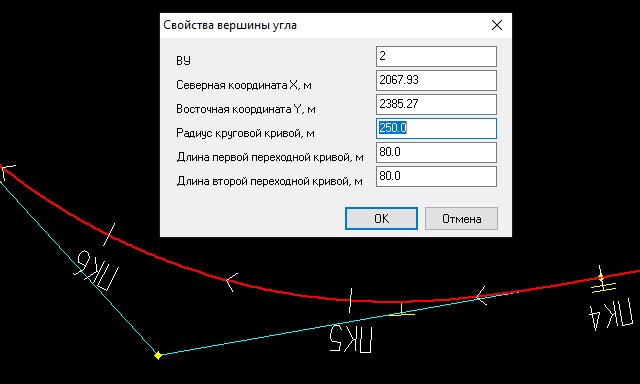
Рис. 6 – Вписываемое закругление в программном продукте «Топоматик Robur»

Порядок проектирования серпантин при проложенном магистральном ходе предлагается следующий:

• выбирают вид закругления – «серпантина», при этом центр основного закругления (x_o1; y_o1) принимают в вершине угла поворота;
• назначают параметры серпантины (R₀; L₀₁; L₀₂; R₁; R₂; L_1д; L_2д; L_1б; L_2б; d₁; d₂), выполняют расчет и построение начальной конфигурации серпантины (рис.7);

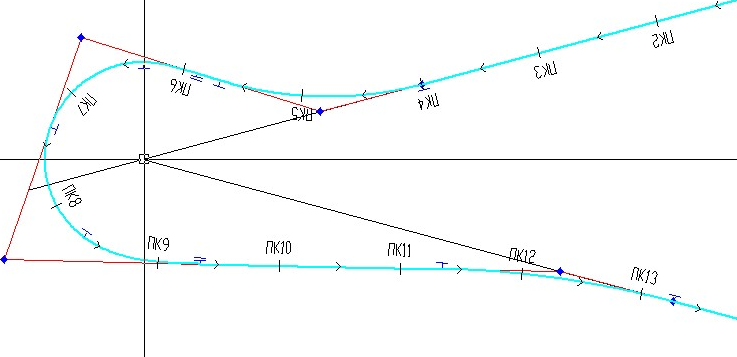
Рис. 7 – Начальная конфигурация серпантины

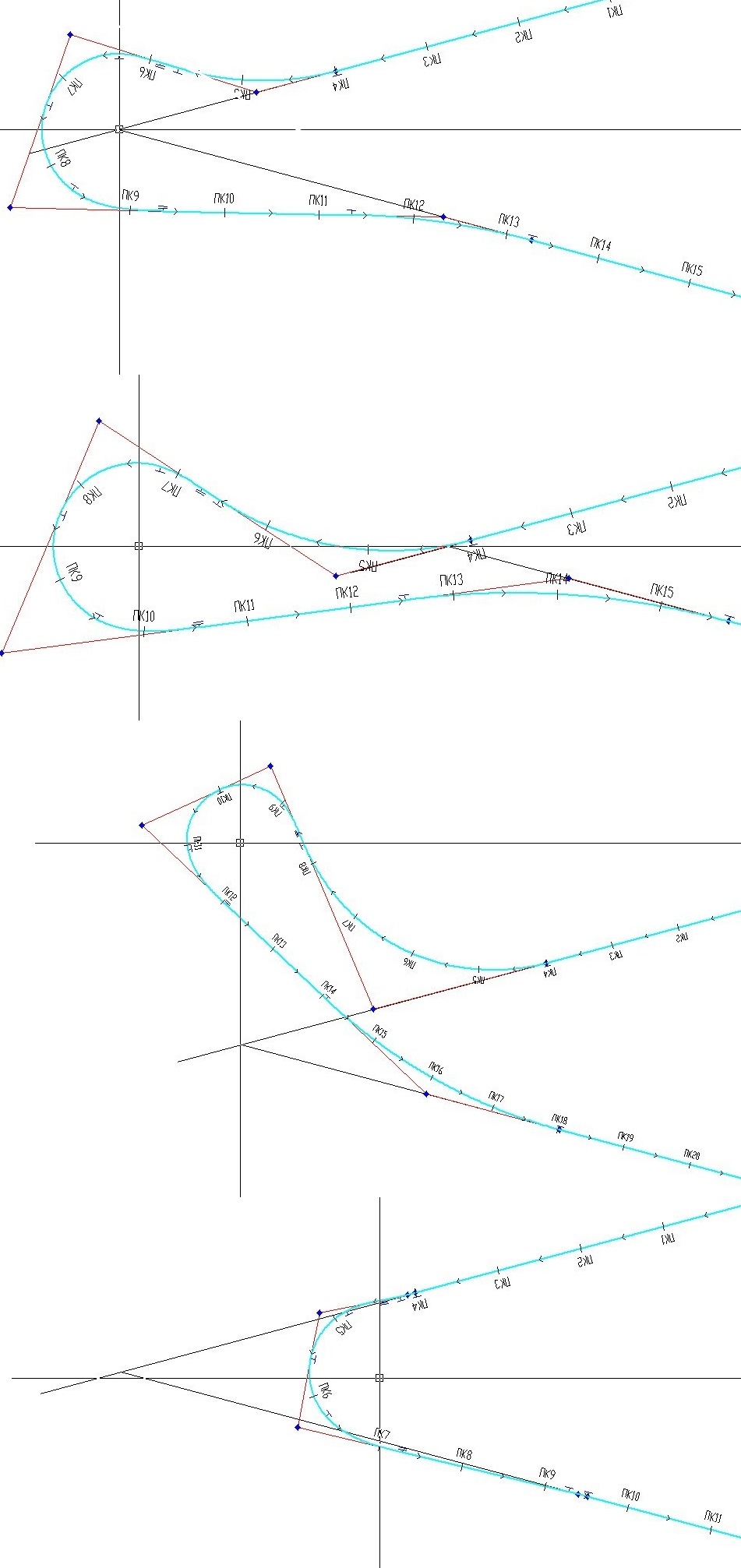
Рис. 8 – Смещение центра основного закругления и визуализация серпантины

• перемещают центр основного закругления с одновременной визуализацией, при необходимости корректируют параметры серпантины, добиваясь наилучшего расположения её на участке проектирования (рис.8);
• «расчленяют» серпантину (при необходимости) на четыре вписанных, стандартных закругления;
• корректируют (при необходимости) параметры расчлененных закруглений.

Для расчета серпантины, используя единый метод расчета [8], требуется знать общие параметры серпантины:

• острый угол серпантины (α);
• направление поворота трассы на серпантине (n);
• положение центра основного закругления в радиальной системе координат (ω и l): угол (ω) отсчитываем против часовой стрелки начиная от биссектрисы острого угла серпантины (α) на центр основного закругления O₁; расстояние (l) измеряем от центра основного закругления до пересечения ветвей серпантины.

Общие параметры серпантины зависят от конфигурации трассы автомобильной дороги на участке проектирования, их вычисляют по известным координатам следующих точек трассы:

ВУ_i-1 – вершина i_-1 угла поворота трассы;

ВУ_i – вершина i-го угла поворота трассы – точка пересечения ветвей серпантины;

ВУ_i+1 – вершина i₊₁ угла поворота трассы;

О_{1 –} центр основного закругления.

Расчет серпантины по единому методу, с использованием, в качестве исходных данных, координаты точек трассы, будем выполнять в следующей последовательности:

1. Расчет дирекционных углов направлений трассы, проходящих через вершину угла поворота: (d_i, d_i+1, d_Б);
2. Нахождение угла поворота трассы (α_i) и его направления (n);
3. Вычисление острого угла серпантины (α) и положение центра основного закругления в радиальной системе координат (ω и l);
4. Вычисление параметров переходных кривых основного и вспомогательных закруглений;
5. Вычисление углов поворота вспомогательных закруглений;
6. Проверка возможности размещения переходных кривых на вспомогательных закруглениях;
7. Расчет угловых параметров серпантины;
8. Расчет тангенсов круговых кривых основного и вспомогательных закруглений;
9. Расчет круговых вставок основного и вспомогательных закруглений;
10. Вычисление координат углов поворота трассы на серпантине в локальной системе координат xy;
11. Вычисление координат углов поворота трассы на серпантине в системе координат проекта XY.

 

Пример расчета серпантины

Основные расчетные зависимости, алгоритмы и последовательность расчета серпантин любого вида и рода рассмотрим на примере (рис.9).

Исходные координаты магистрального хода и центра основного закругления представлены в таб.1, параметры серпантины в табл.2

Таблица 1 – Координаты точек плана трассы на участке проектирования

Точка	Координаты с системе координат проекта
	X (север)		Y (восток)
	Обозначение	Величина, м	Обозначение	Величина, м
ВУi-1	Xi-1	8 533,62	Yi-1	18 848,81
ВУi	Xi	8 935,00	Y i	18 771,38
ВУi+1	Xi+1	8 669,92	Yi+1	18 993,36
О1	XO1	8 957,45	YO1	18 702,76

Последовательность расчета:

1. Вычисляем дирекционные углы направлений используя блок-схему алгоритма (рис.4):

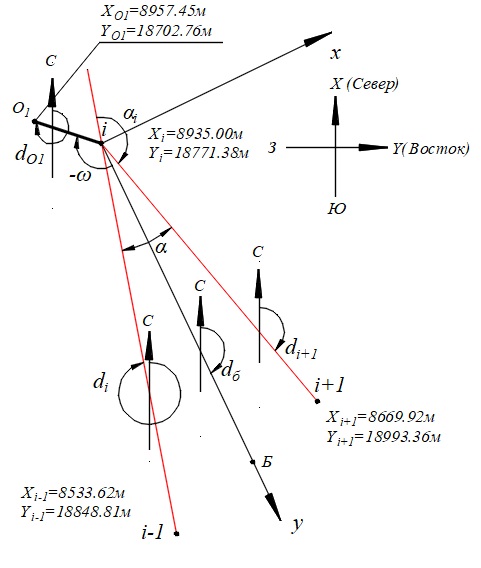
Рис. 9 – Исходные координаты трассы

Направление: Начало участка – пересечение ветвей серпантины:

Направление: Пересечение ветвей серпантины –конец участка:

Направление: Пересечение ветвей серпантины –центр основного закругления:

Таблица 2 – Исходные параметры серпантины

ы

№ пп	Параметр	Обозначение	Единица измерения	Величина
1	Радиус основного закругления	R0	м	80
2	Длина переходной кривой в начале основного закругления	L01	м	50
3	Длина переходной кривой в конце основного закругления	L02	м	45
4	Радиус круговой кривой первого вспомогательного закругления	R1	м	350
5	Длина переходной кривой в начале первого вспомогательного закругления	L1д	м	100
6	Длина переходной кривой в конце первого вспомогательного закругления	L0б	м	90
7	Прямая вставка между первым вспомогательным закруглением и основным закруглением	d1	м	30
8	Радиус круговой кривой первого вспомогательного закругления	R2	м	500
9	Длина переходной кривой в начале первого вспомогательного закругления	L2б	м	120
10	Длина переходной кривой в конце первого вспомогательного закругления	L2д	м	110
11	Прямая вставка между вторым вспомогательным закруглением и основным закруглением	d2	м	10

Направление: Пересечение ветвей серпантины – биссектриса острого угла серпантины:

Вначале найдем координаты точки Б (рис.9), расположенной на биссектрисе, для этого вычислим:

Расстояние между точками (i… i-1):

Расстояние между точками  (i,… i+1):

Тогда координаты точки определим по формулам:

2. Вычисляем угол поворота трассы на серпантине и направление поворота используя блок-схему алгоритма (рис.5):Так какдля вычисления угла поворота трассы на серпантине воспользуемся формулой:

Знак угла поворота трассы – положительный, трасса поворачивает на право, направление поворота трассы на серпантине

3. Вычисляем острый угол серпантины и положение центра основного закругления:

Острый угол серпантины определим через угол поворота трассы на серпантине:

где –абсолютное значение угла поворота трассы на вершине ВУ_i..

Острый угол серпантины:

Угол смещения центра основной кривой определим, используя блок-схему алгоритма для вычисления углов поворота трассы (рис.5). Так как  для вычисления угла ω воспользуемся формулой:

Расстояние смещения центра основной кривой l определим по формуле:

4. Вычисление параметров переходных кривых основного и вспомогательных закруглений:

4.1 Углы поворота трассы, относящиеся к переходным кривым, рад.:

.2 Тангенсы переходных кривых:

4.3 Сдвижки круговых кривых:

5. Вычисление углов поворота вспомогательных закруглений, используя блок-схему алгоритма (рис. 10):

5.1 Первое вспомогательное закругление i = 1:

Примем m=1 и вычислим следующие коэффициенты:

Подкоренное выражение:

 

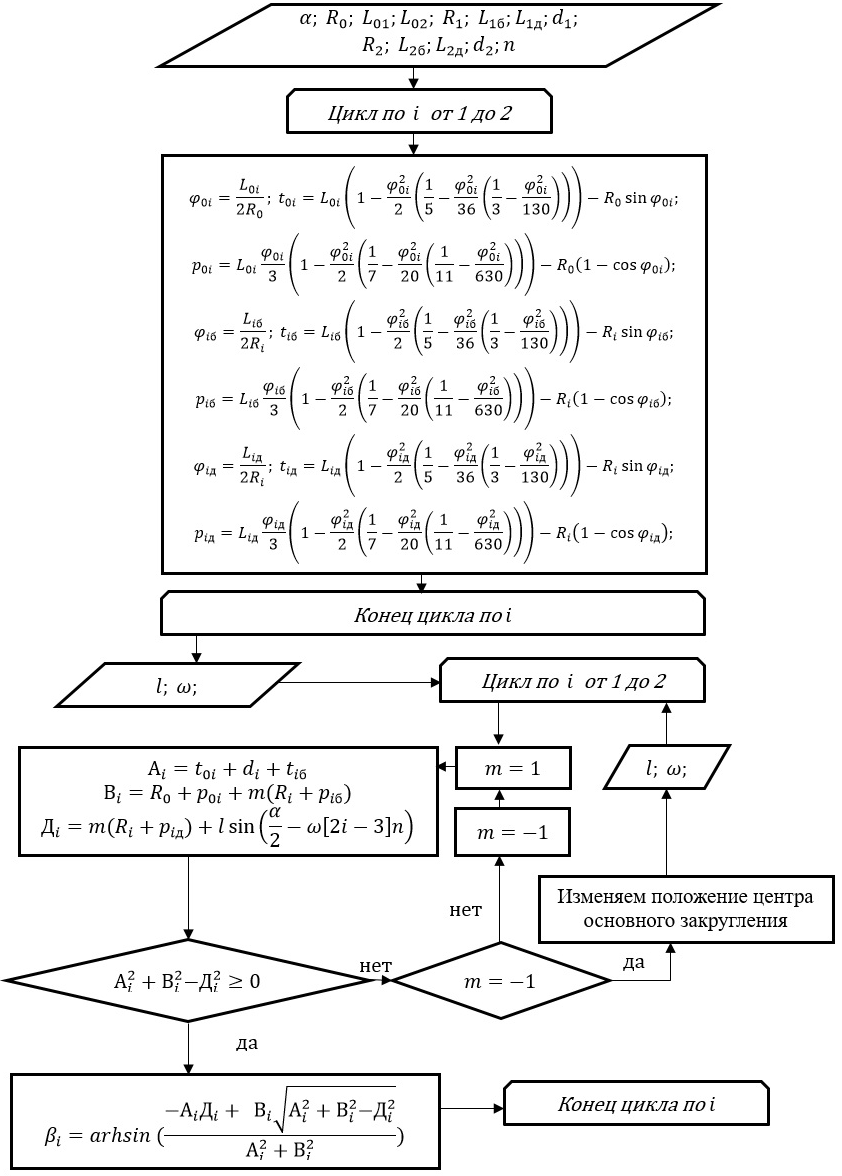
Рис. 10 – Алгоритм вычисления углов поворота вспомогательных закруглений серпантин

Так как подкоренное выражение положительное, вычислим угол поворота первого вспомогательного закругления:

Переведем в градусную меру: β₁(град) = 36^о 29’56”.

5.2 Второе вспомогательное закругление i = 2:

Примем m=1 и вычислим следующие коэффициенты:

Подкоренное выражение:

Так как подкоренное выражение положительное, вычислим угол поворота второго вспомогательного закругления:

Переведем в градусную меру: β₁(град) = 14^о 49’ 47”.

6. Проверим возможность размещения переходных кривых на вспомогательных закруглениях:

6.1 Первое вспомогательное закругление:

Условие размещения выполняется.

6.2 Второе вспомогательное закругление:

Условие размещения выполняется.

7. Расчет угловых параметров серпантины:

Часть угла поворота первого вспомогательного закругления, приходящаяся на круговую вставку:

Часть угла поворота второго вспомогательного закругления, приходящаяся на круговую вставку:

Угол поворота трассы на серпантине:

Часть угла поворота основного закругления, приходящаяся на круговую вставку:

Первая половина угла поворота основного закругления:

Переведем в градусную меру: 

Вторая половина угла поворота основного закругления:

Переведем в градусную меру: 

8. Расчет тангенсов круговых кривых основного и вспомогательных закруглений:

8.1 Первое вспомогательное закругление:

8.2 Второе вспомогательное закругление:

8.3 Основное закругление:

9. Расчет круговых вставок основного и вспомогательных закруглений:

Первое вспомогательное закругление:

Второе вспомогательное закругление:

Основное закругление:

Ведомости углов поворота, прямых и кривых трассы автомобильных дорог формируют, как правило, используя координаты углов поворота трассы.

10. Вычислим координаты углов поворота трассы на серпантине в локальной системе координат xy (рис.9), используя в качестве исходных данных координаты точки пересечения ветвей серпантины (x_o=0.00; y_o=0.00):

10.1. Координаты центра основного закругления O₁:

10.2. Координаты вершины угла поворота первого вспомогательного закругления ВУ₁:

10.3. Координаты вершины угла поворота второго вспомогательного закругления ВУ₂:

10.4. Координаты вершины угла поворота первой половины основного закругления ВУ₀₁:

10.5. Координаты вершины угла поворота второй половины основного закругления ВУ₀₂:

11. Вычислим координаты углов поворота трассы на серпантине в системе координат проекта XY, используя в качестве исходных данных координаты точки пересечения ветвей серпантины (Xo=8935.00 м; Yo=18771.38 м, дирекционный угол биссектрисы острого угла серпантины  и координаты точек в локальной системе координат:

11.1. Координаты вершины угла поворота первого вспомогательного закругления ВУ₁:

11.2. Координаты вершины угла поворота второго вспомогательного закругления ВУ₂:

11.3. Координаты вершины угла поворота первой половины основного закругления ВУ₀₁:

11.4. Координаты вершины угла поворота второй половины основного закругления ВУ₀₂:

Результаты расчета серпантины приведены на рис. 11

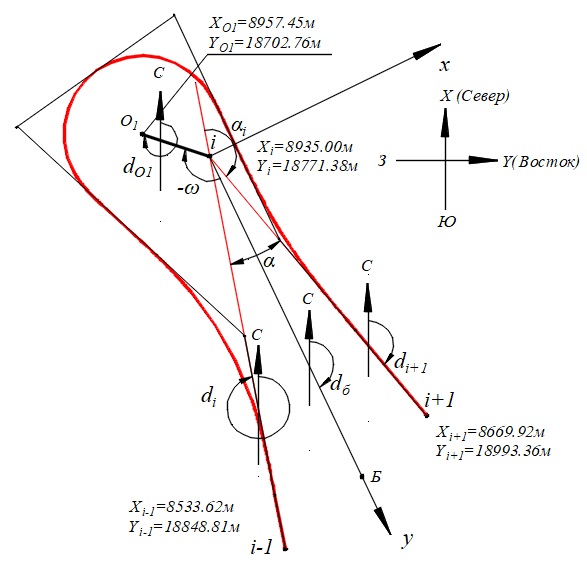
Рис. 11 – Серпантина полученная по результатам расчета с использованием координат точек трассы

Используя разработанный алгоритм запроектирован участок серпантинных трасс (рис.12). Алгоритм расчета серпантин является общим и универсальным, может быть внедрен в любой программный комплекс проектирования автомобильных дорог.

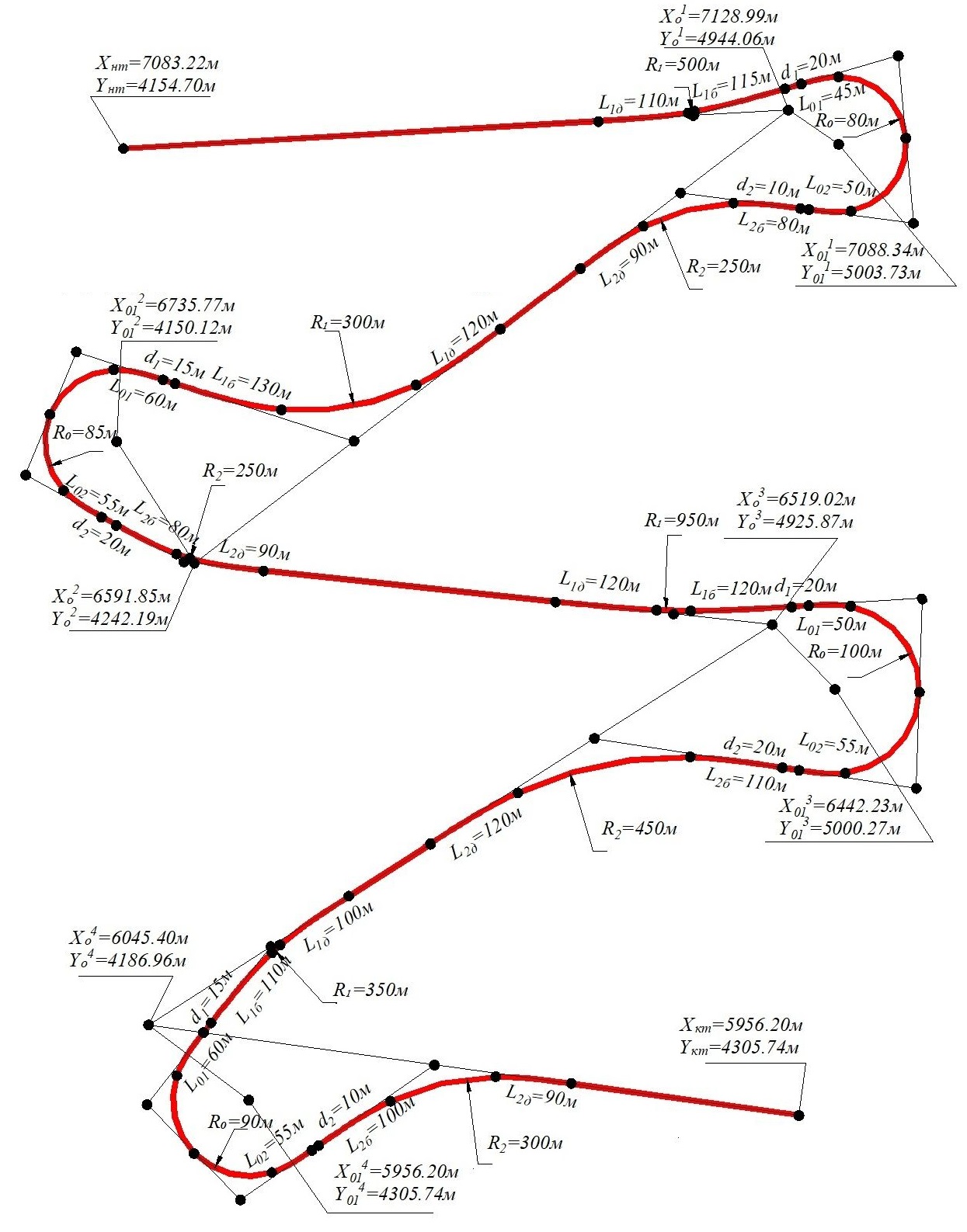
Рис. 12 – Исходные данные и результат расчета трассы на участке каскада серпантин

 

Заключение

В САПР АД отсутствует понятие серпантин как единого сложного закругления, что значительно усложняет проектирования. Проектировщик «собирает» комбинированное закругление из отдельных (трех, четырех и более) сложных, вписанный закруглений – с круговой вставкой и двух клотоид. Другими словами, проектирование серпантины сводится не к её расчету, а к графическому конструированию серпантинных закруглений.

До исследований, выполненных авторами настоящей статьи, не было способов расчета серпантины с несимметричными вспомогательными закруглениями и отсутствовала практика однозначного и достоверного расчета серпантин со смещенным центром основного закругления.

В настоящей статье разработаны предложения по автоматизации расчета серпантин любого вида и рода, в том числе сложных серпантин с несимметричными вспомогательными закруглениями. Основные зависимости и последовательность расчета базируются на разработанном ранее общем методе расчета серпантин.

В результате проведенных исследований:

• усовершенствован метода расчета серпантин для использования в цифровых моделях автомобильных дорог;

• разработаны алгоритмы автоматизации расчетов и проектирования серпантин в САПР АД;
• предложены решения по визуализации процесса проектирования серпантин с использованием САПР АД.

В статье приведены не только алгоритмы расчета, но численный пример их реализации. Внедрение указанных алгоритмов значительно упростит процедуру проектирования серпантинных трасс, повысит качество и надежность принимаемых проектных решений.

Конфликт интересов  Не указан.

Conflict of Interest  None declared.