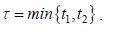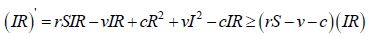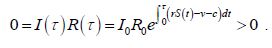О НЕЛИНЕЙНОЙ ДИФФЕРЕНЦИАЛЬНОЙ СИСТЕМЕ, МОДЕЛИРУЮЩЕЙ ДИНАМИКУ ПАНДЕМИИ COVID-19

О НЕЛИНЕЙНОЙ ДИФФЕРЕНЦИАЛЬНОЙ СИСТЕМЕ, МОДЕЛИРУЮЩЕЙ ДИНАМИКУ ПАНДЕМИИ COVID-19

Научная статья

Звягинцев А.И. ^*

ORCID: 0000-0003-0199-6420,

Михайловская военная артиллерийская академия, Санкт-Петербург, Россия

^* Корреспондирующий автор (azvyagintsev[at]mail.ru)

Аннотация

В статье на основе классической SIR-модели распространения инфекционной эпидемии разработана математическая модель SVIR, учитывающая особенности распространения коронавирусной пандемии COVID-19. В созданной модели, в отличие от базовой, учитывается возможность повторного заражения коронавирусом и процесс вакцинации населения. Кроме того, в SVIR-модели отражен фактор изменения численности населения в результате рождаемости и смертности (включая от коронавируса) и в силу миграции населения. При моделировании прогнозов по динамике заболеваемости COVID-19 прежде всего интересует периодичность повторения коронавирусных волн и насколько последующая волна превысит предыдущую. В статье доказаны теоремы, гарантирующие возможность моделирования волнообразной динамики заболеваемости коронавирусом. На основе полученных теорем приводится пример численного моделирования волнообразной траектории.

Ключевые слова: математическая модель, дифференциальные уравнения, краевая задача, распространение эпидемии, пандемия COVID-19.

ON A NONLINEAR DIFFERENTIAL SYSTEM SIMULATING THE DYNAMICS OF THE COVID-19 PANDEMIC

Research article

Zvyagintsev A.I.^*

ORCID: 0000-0003-0199-6420,

Mikhailovskaya Military Artillery Academy, Saint Petersburg, Russia

^* Corresponding author (azvyagintsev[at]mail.ru)

Abstract

In the article, based on the classical SIR model of the spread of an infectious epidemic, a mathematical SVIR model has been developed that takes into account the specifics of the COVID-19 coronavirus pandemic spread. The created model, unlike the basic one, takes into account the possibility of re-infection with coronavirus and the process of vaccination of the population. In addition, the SVIR model reflects the factor of population change as a result of birth rate and mortality (including from coronavirus) and migration. When modeling forecasts for the dynamics of the incidence of COVID-19, the factors of frequency of repetition of coronavirus waves and how the next wave will exceed the previous one are of particular interest. The article proves theorems that guarantee the possibility of modeling the wave-like dynamics of the incidence of coronavirus. Based on the obtained theorems, an example of numerical simulation of a wave-like trajectory is presented.

Keywords: mathematical model, differential equations, boundary value, epidemic spread, COVID-19 pandemic.

Введение

Последствия медицинского шока в форме пандемии COVID-19 оказали огромное влияние на социально-экономическую обстановку во всем мире. По данным Всемирной организации здравоохранения, по состоянию на 6 мая 2022 года вирусом COVID-19 во всем мире заразилось более 513,9 миллиона человек и более 6,2 миллиона умерло [1].

Математические модели, описывающие распространение эпидемии COVID-19, начали разрабатываться практически одновременно с первой вспышкой заболевания в Китае в январе 2020 г. В основе многих таких моделей используется SIR–модель распространения инфекции, предложенная В.Кермаком и А.Маккендриком [2]. Эта математическая модель состоит из трех дифференциальных уравнений и включает три группы индивидов (в зависимости от отношения к болезни): восприимчивые к заболеванию (Susceptible), инфицированные (Infected) и выздоровевшие (Recovered).

Идеи, заложенные в SIR-модели, послужили толчком для дальнейших исследований различных ученых. Путем модификации этой модели было разработано множество математических моделей распространения инфекционных заболеваний (SIS, SEI, SIRS, SEIS, SEIR, SEIRS, MSIR, MSEIR, MSEIRS, LISEIR) [3], [4], учитывающих разное число групп, участвующих в эпидемическом процессе, и включающих многообразное количество параметров, влияющих на течение эпидемии.

Отдельные эксперты считают ошибочным использование SIR-моделей для описания пандемии коронавируса [5]. Действительно, в этой модели считается, что переболевшие индивиды приобретают иммунитет и не могут быть заражены вторично. Для пандемии COVID-19 это предположение не выполняется. Более того, в SIR–модели предполагается постоянство численности населения и не учитывается процесс вакцинации от вирусной инфекции. Наконец, существенным недостатком большинства разработанных модификаций SIR–модели является их неспособность имитировать циклические процессы, которые характерны для волнообразной динамики заболеваемости коронавирусом, причем эта динамика иногда приобретает «пилообразный» вид. Такая картина, например, наблюдалась в России во время максимального пика распространения коронавирусной пандемии в феврале 2022 года [6], что наглядно демонстрирует рисунок 1.

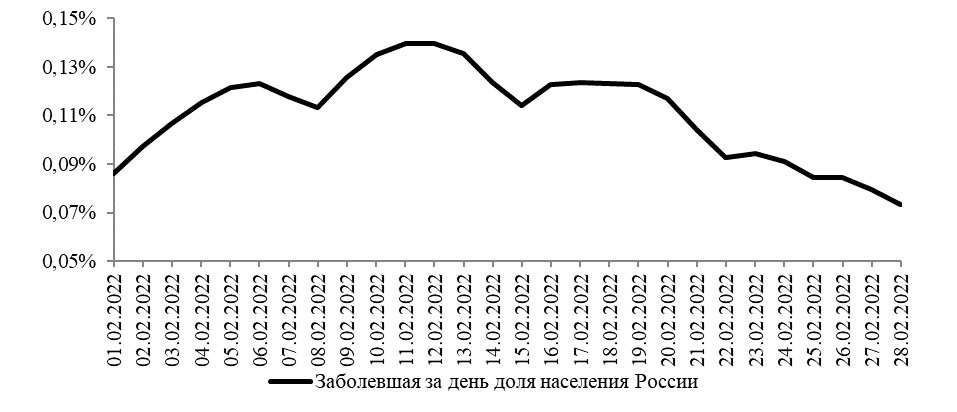Рис. 1 – Заболеваемость коронавирусом в России в феврале 2022 года

В данной статье будет предложена такая модификация SIR–модели, которая устраняет перечисленные выше недостатки. Кроме того, будут доказаны теоремы, гарантирующие возможность моделирования волнообразной динамики заболеваемости коронавирусом. Полученные в статье результаты являются дополнением к исследованиям по математическому моделированию пандемии COVID-19, обзоры которых содержатся, например, в работах [7], [8], [9].

Методы и принципы исследования              

Разработанная В.Кермаком и А.Маккендриком [2] модель является классической SIR–моделью. В ней рассматривается три группы индивидов – восприимчивые к заболеванию (Susceptible), инфицированные (Infected) и выздоровевшие (Recovered). Передача инфекции осуществляется от инфицированных индивидов к восприимчивым. Модель описывается системой 3-х дифференциальных уравнений:

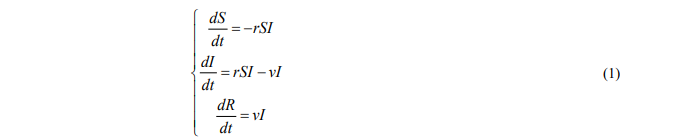
Здесь 𝑆(𝑡),𝐼(𝑡),𝑅(𝑡) − численности восприимчивых, инфицированных и переболевших индивидов в момент времени tсоответственно; 𝑟 − коэффициент скорости передачи инфекции; ν − коэффициент интенсивности выздоровления инфицированных индивидов.

В SIR–модели (1) исключается возможность повторного заражения для переболевших индивидов, что не соответствует пандемии COVID-19. Кроме того, в модели (1) подразумевается постоянство численности населения и не предусматривается процесс вакцинации от вирусной инфекции. В этой связи осуществим модификацию SIR–модели: добавим «вакцинное» уравнение (Vaccinated) и введем дополнительные параметры.

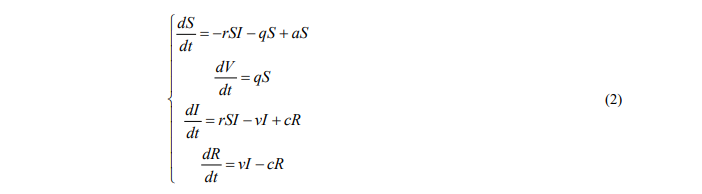
Здесь 𝑆(𝑡), V(t), 𝐼(𝑡), 𝑅(𝑡) – соответственно численности подверженных риску заражения (не болевших COVID, но и не сделавших прививку), полностью вакцинированных (двумя дозами), больных коронавирусом, выздоровевших граждан; 𝑟 − коэффициент скорости заражения COVID; ν − коэффициент интенсивности выздоровления инфицированных индивидов; q – коэффициент вакцинации; с− коэффициент повторного заражения COVID; a − коэффициент флуктуации населения, который учитывает эффект изменения численности населения в результате рождаемости и смертности (включая от коронавируса) и в силу миграции населения. Полученную систему (2) назовем SVIR-моделью.

При численном моделировании используются начальные условия

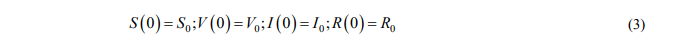
Но при моделировании прогнозов по динамике заболеваемости COVID-19 прежде всего интересует периодичность повторения коронавирусных волн и насколько последующая волна превысит предыдущую. В этой связи возникает необходимость рассмотрения краевых условий

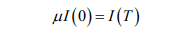
где Т – временной период до появления новой коронавирусной волны. Если коэффициент 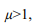, то новая коронавирусная волна превысит предыдущую, а в случае  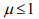ситуация будет обратной.

Для успешной реализации практического моделирования важно установить критерии и условия, при которых существует возможность конструированиякоронавирусных волн. В дальнейшим нам понадобится известный результат из теории краевых задач [10]. Рассмотрим систему обыкновенных дифференциальных уравнений

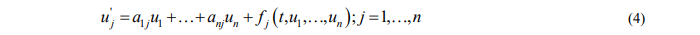
с краевыми условиями

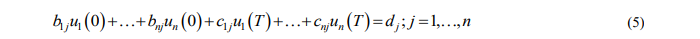
где 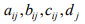– вещественные числа 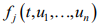– непрерывные и ограниченные функции на отрезке [0,Т].
Теорема 1 (о существовании решения)
Если соответствующая однородная задача

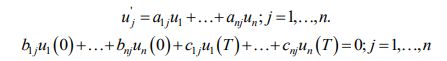
имеет только нулевое решение, то решение исходной краевой задачи (4)-(5) существует.
Отметим, что в монографии [10, С. 24–25] доказана теорема существования для более общего случая.
Основные результаты
Докажем теоремы, обуславливающие возможность применения системы (2) для моделирования волнообразной
динамики распространения коронавирусной инфекции.
Теорема 2. Если числа 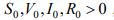, то решение системы (2) с начальными условиями (3) положительно на
любом отрезке [0,Т] .
Доказательство. 1) В результате интегрирования первого уравнения системы (2) получаем

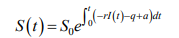
Отсюда следует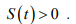 

2) Для второго уравнения системы (2) в силу доказанного пункта 1) имеем 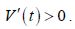Следовательно, функция V(t)
является возрастающей и с учетом V(0) >0 получается V(t) >0.

3) Докажем, что I(t) >0 и R(t) >0 . Если предположить противное, то найдутся такие 1 t и 2t , что I(t) >0 на интервале
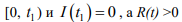 на интервале  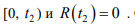Обозначим 
Сложив третье уравнение системы (2), умноженное на R, с четвертым уравнением, умноженным на I, получаем

Интегрируя это неравенство от 0 до τ , получаем противоречие
 

Теорема доказана.
Теорема 3. Если числа 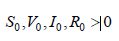, то решение системы (2) с начальными условиями (3) ограничено на
отрезке [0,Т] .
Доказательство. Численность населения в момент времени t составляет
N (t ) = S (t ) +V (t ) + I (t ) + R(t )
В силу теоремы 2 имеем

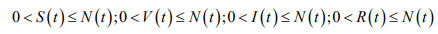
Сложив все уравнения системы (2) получаем

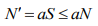
Интегрируя это неравенство, получаем

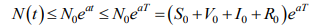
В случае a<0 вместо e^aT будет e⁰=1. Теорема доказана.
Рассмотрим краевую задачу:

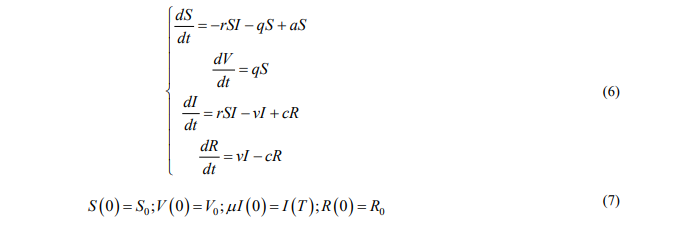
Теорема 4. Пусть 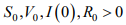и выполняются условия

Тогда краевая задача (6)-(7) имеет решение.
Доказательство. 1) Обозначим

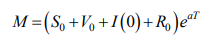
Вместо исходной системы (6) рассмотрим модифицированную систему

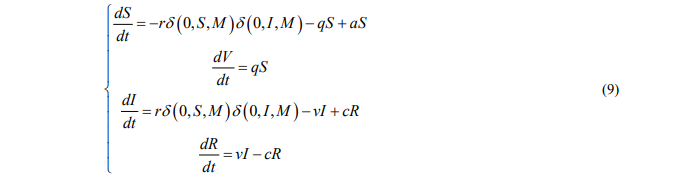
Здесь дельта-функция определяется следующим образом

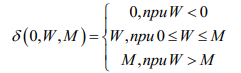
Ясно, что нелинейную часть системы (9) составляют непрерывные и ограниченные функции. Запишем
соответствующую однородную задачу:

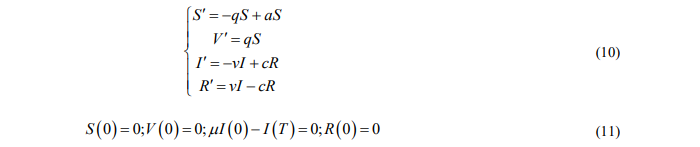
Из первых двух уравнений системы (10) получаем

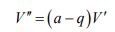
Из третьего и четвертого уравнений системы (10) имеем

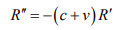
Для этих дифференциальных уравнений второго порядка соответствующие характеристические уравнения имеют
вид

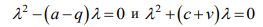
Вычислив корни характеристических уравнений, получаем общее решение системы (10):

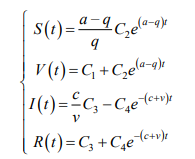
Здесь 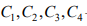 –произвольные действительные числа. На основании условий (11) получаем алгебраическую
систему уравнений

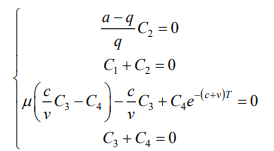
Эта система в силу (8) имеет единственное решение 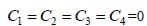 . Следовательно, у однородной задачи
(10)-(11) существует единственное решение, тождественно равное нулю. Тогда по теореме 1 модифицированная
система (9) с краевыми условиями (7) имеет решение

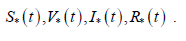
2) Покажем, что 

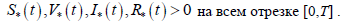
А) Если предположить нарушение неравенства 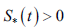, то найдутся такие  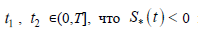на
интервале 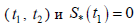 . Кроме того, для  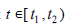первое уравнение системы (9) примет вид ,
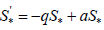решение которого приводит к противоречию

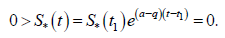
Б) Если предположить нарушение неравенства 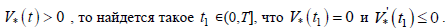 Но тогда с учетом пункта А) из второго уравнения системы (9) следует противоречие

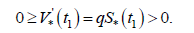
В) Если предположить нарушение неравенства 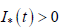 то в силу краевых условий  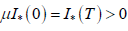 найдутся
такие 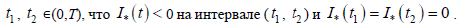 Кроме того, для  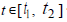уравнение
системы (9) примет вид 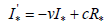 с помощью четвертого уравнения системы (9) приводится к
уравнению второго порядка 

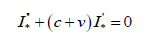
Общее решение этого уравнения 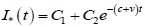 Из условий  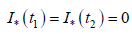0 получаем систему
уравнений

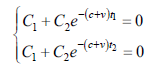
Отсюда 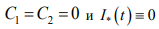 на отрезке [ t₁, t₂ ] , что противоречит  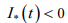на интервале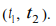 

 Г) Если предположить нарушение неравенства 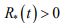 , то найдется такое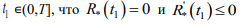 

Но тогда с учетом пункта В) из четвертого уравнения системы (9) следует противоречие

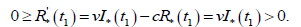
3) Покажем, что 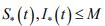на всем отрезке [0,T] .
Сложив все уравнения системы (9) и с учетом пункта 2) получаем

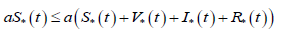
Повторяя рассуждения из доказательства теоремы 3, получим для всех tε[0,T] неравенство

 

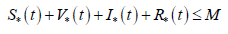
Отсюда в частности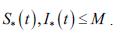 

4) На основании пунктов 2) и 3) имеем 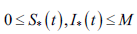на всем отрезке [0,T] . Отсюда следует, что  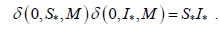Это означает, что для функций  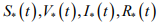модифицированная система
(9) совпадает с исходной системой (6). Таким образом, 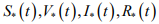 является решением исходной краевой
задачи (6)-(7). Теорема доказана.
В качестве примера на рисунке 2 представлен график волнообразной динамики коронавирусной заболеваемости,
смоделированный в результате решения краевой задачи (6)–(7).

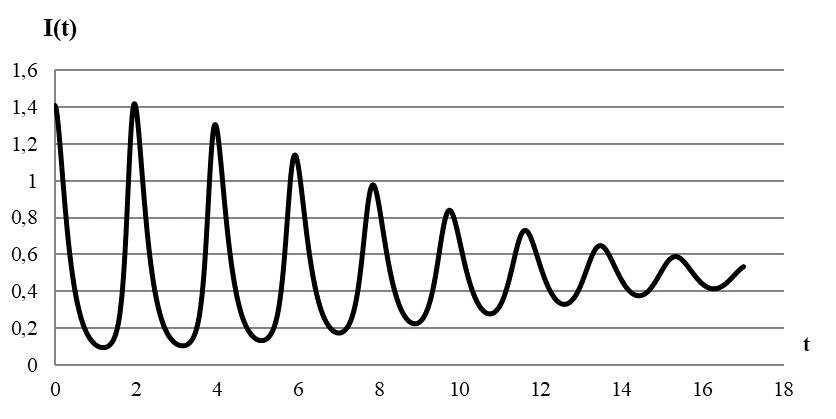
Рис. 2 – Смоделированная волнообразная динамика заболеваемости коронавирусом

Численное решение дифференциальной системы (6) находится методом Рунге-Кутта [11, С.201]. В результате
компьютерного эксперимента были подобраны численные значения параметров краевой задачи (6)-(7):

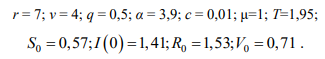
График рисунка 2 имеет «пилообразный» вид, что соответствует конфигурации коронавирусной динамики большинства стран в первом квартале 2022 года [1], [6].

Заключение

В результате модификации классической SIR-модели разработана новая SVIR-модель, которая способна генерировать сценарии волнообразного распространения COVID-19. Полученные в статье теоремы обеспечивают возможность моделирования волнообразной динамики заболеваемости коронавирусом. Для осуществления такого моделирования необходимо решать краевую задачу. Теорема 4 определяет допустимую область параметров, вариация которыми позволяет имитировать динамику COVID пандемии. Теоремы 2 и 3 определяют границы возможных колебаний для показателей коронавирусной динамики.Разработанная SVIR-модель может служить практическим инструментарием для адекватного прогнозирования возникновения новых волн COVID-19.

 

Конфликт интересов  Не указан.

Conflict of Interest  None declared.