ОПЫТ ПРИМЕНЕНИЯ MATHCAD В ИССЛЕДОВАТЕЛЬСКИХ ЗАДАЧАХ ПО ДЕРЕВООБРАБОТКЕ
ОПЫТ ПРИМЕНЕНИЯ MATHCAD В ИССЛЕДОВАТЕЛЬСКИХ ЗАДАЧАХ ПО ДЕРЕВООБРАБОТКЕ
Обзорная статья
Бегункова Н.О.*
ORCID: 0000-0001-5069-9604,
Тихоокеанский государственный университет, Хабаровск, Россия
* Корреспондирующий автор (natali-beg[at]mail.ru)
Аннотация
В статье рассматривается возможность применения математических систем при исследованиях в области деревообработки, когда требуется выполнять большое количество математических операций и вычислений различного уровня сложности. Основной акцент сделан на применении математического пакета Mathcad для подробного описания решения двух исследовательских задач в области деревообработки, а также показаны возможности данного пакета для графической интерпретации результатов, полученных при решении одной из задач. Можно сказать, что в пакете Mathcad подобные задачи решаются достаточно быстро, поскольку он имеет понятный, удобный и простой пользовательский интерфейс, что позволяет снизить временные затраты на проведение однообразных вычислений вручную.
Ключевые слова: исследование, деревообработка, Mathcad.
EXPERIENCE OF MATHCAD APPLICATION TO WOODWORKING RESEARCH PROBLEMS
Review article
Begunkova N.O.*
ORCID: 0000-0001-5069-9604,
Pacific State University, Khabarovsk, Russia
* Corresponding author (natali-beg[at]mail.ru)
Abstract
The article considers the possibility of application of mathematical systems in research in the sphere of wood processing, when it is necessary to perform numerous mathematical operations and calculations of various levels of complexity. The main emphasis is placed on the application of the mathematical package Mathcad for detailed description of the solution of two research problems in the sphere of wood processing; the possibilities of this package for graphical interpretation of the results obtained when solving one of the problems are also shown. The Mathcad package can be said to solve such problems promptly, since it has a simple and user-friendly interface, which allows reducing the time required to perform repetitive calculations manually.
Keywords: research, wood processing, Mathcad.
Введение
Последние годы цифровизация исследовательских работ развивается достаточно быстро. При этом для выполнения разнообразных инженерных расчетов в современных научных исследованиях привлекаются различные прикладные программные продукты: CAD-, CAM-, CAE-системы [1]. Применение таких продуктов ускоряет и облегчает процесс обработки экспериментальных данных, предоставляет широкие возможности для их визуализации и построения виртуальных моделей объектов исследования, что сегодня является актуальным вопросом для совершенствования процессов деревообработки.
Основная часть
Комплексное использование древесного сырья является необходимым условием повышения конкурентоспособности продукции деревообрабатывающей промышленности [2]. Этому во многом способствует также постоянный поиск путей совершенствования технологий изготовления изделий из древесины [3], [4]. В связи с этим проводятся различные научно-исследовательские эксперименты, достаточно трудоемкие и требующие, как правило, соответствующего оборудования и древесных ресурсов.
Однако сегодня все в большей степени исследования проводятся виртуально на математических моделях, имитирующих соответствующие технологические процессы. В ходе их осуществления очень часто приходится иметь дело с обработкой достаточно сложных и порою объемных математических вычислений: нахождение многочисленных коэффициентов полинома, описывающего характер изменения какой-либо исследуемой характеристики материала [3], [4] (например, толщины древесно-стружечных плит в зависимости от условий прессования), применение кратных интегралов для расчета объемов тел сложной формы (например, пустотелого бруса, брусьев переменного сечения) и т. п.
В связи с этим все чаще используются возможности современных программных продуктов, в том числе математических систем, предоставляющих пользователю широкий спектр инструментов и средств визуализации для работы с математическими выражениями различного уровня сложности. К ним можно, в частности, отнести Mathcad, Maple, Matlab и другие подобные системы [5], [6], [7], [8]. У каждой из них есть свои особенности, преимущества и недостатки, знание и учет которых помогает выбрать более подходящую из них для решения той или иной поставленной задачи [1], [9].
Одной из таких задач являлось вычисление объема пустотелого бруса, состоящего из сегментов переменного сечения. Такой брус можно получить из тонкомерного сырья и использовать в качестве полноценного конструкционного пиломатериала, используемого в том числе в деревянном домостроении. На рисунке 1 представлена схема получения такого бруса при продольном раскрое круглого лесоматериала параллельно его оси. Необходимость расчета объема такого бруса связана с последующим использованием данного показателя при расчете массы бруса и его нагрузки в различных конструкциях.
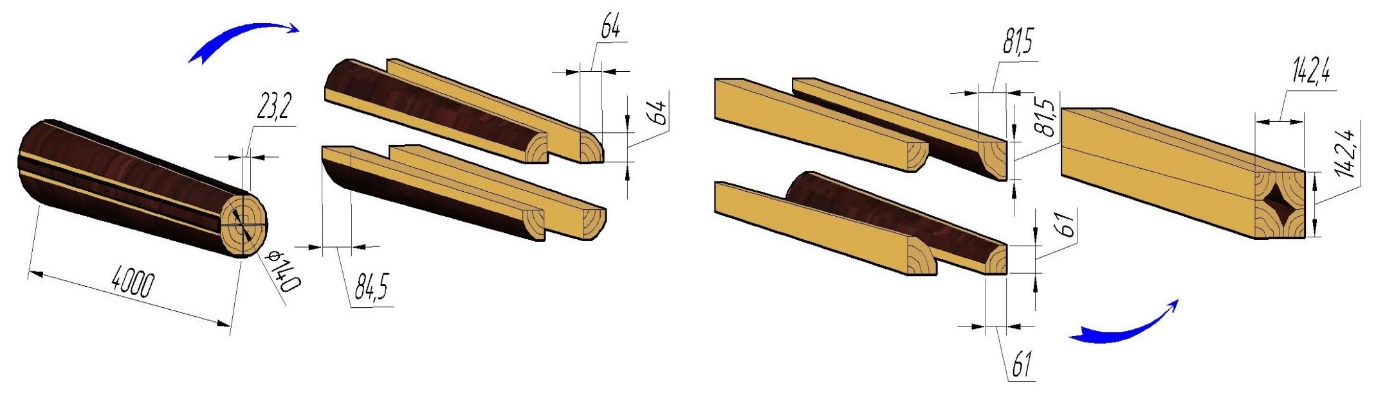
Рис. 1 – Схема получения пустотелого бруса
Предполагая, что круглый лесоматериал, из которого изготавливается пустотелый брус, представляет собой усеченный конус, от которого с четырех сторон отсекаются параллельно образующей горбыли, можно воспользоваться известной формулой объема усеченного конуса и приложением интегрального исчисления для определения объема тела вращения. В итоге после ряда математических преобразований получаются следующие выражения:
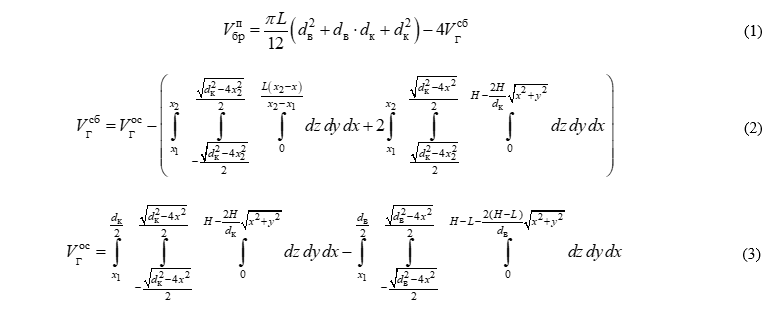
где 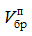 – объем пустотелого бруса; L – длина круглого лесоматериала; dв, dк – диаметр круглого лесоматериала соответственно в вершинной и в комлевой его частях;
– объем пустотелого бруса; L – длина круглого лесоматериала; dв, dк – диаметр круглого лесоматериала соответственно в вершинной и в комлевой его частях;  ,
, 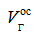 – объем горбыля, отпиливаемого параллельно соответственно образующей или оси бревна; x1, x2 – расстояние между осью бревна и плоскостью пиления горбыля соответственно в вершинной и комлевой частях бревна; H – величина, рассчитываемая по формуле:
– объем горбыля, отпиливаемого параллельно соответственно образующей или оси бревна; x1, x2 – расстояние между осью бревна и плоскостью пиления горбыля соответственно в вершинной и комлевой частях бревна; H – величина, рассчитываемая по формуле:
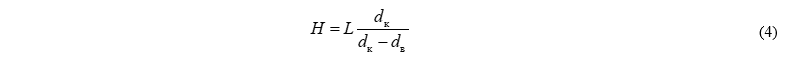
Значения для расстояний x1 и x2 вычисляются по формулам:
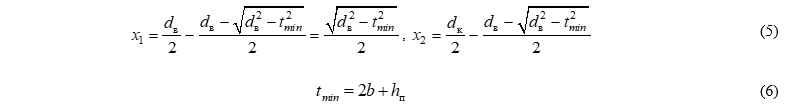
где b – ширина фаски склеивания, hп – толщина пропила.
Подставляя требуемые исходные данные в выражения (1)–(6) рассчитывается объем пустотелого сырого бруса, состоящего из сегментов переменного сечения, образующихся при продольном раскрое круглого лесоматериала параллельно его оси.
Если пустотелый брус планируется получать из сегментов постоянного сечения, то продольный раскрой бревна будет выполняться параллельно его образующей. В этом случае при расчете объема этого бруса необходимо в выражении (1) вычесть еще объем  получаемого в центре бревна при таком раскрое остатка клиновидной формы, который можно определить из следующих выражений:
получаемого в центре бревна при таком раскрое остатка клиновидной формы, который можно определить из следующих выражений:
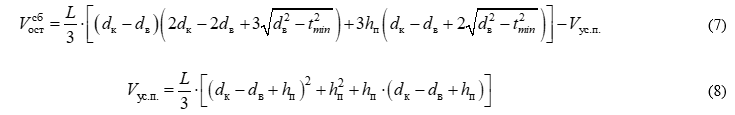
Вычитая этот объем  из значения, полученного по формуле (1):
из значения, полученного по формуле (1):
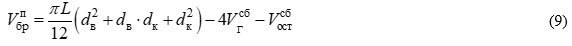
определяют объем пустотелого сырого бруса, состоящего из сегментов постоянного сечения, получающихся при продольном раскрое круглого лесоматериала параллельно его образующей.
Очевидно, что проведение расчетов вручную по представленным формулам (1)–(9) довольно трудоемко. Поэтому возникает необходимость использования соответствующих программных продуктов.
В данном случае удобнее всего воспользоваться инструментами, предоставляемыми математическим пакетом Mathcad, отличающимся от других подобных систем прежде всего возможностью набора формул и функций в привычной математической нотации (деление, умножение, квадратный корень, интеграл и т. д.), не требующей изучения нового синтаксиса или наличия навыков программирования, а также интуитивно понятным для пользователя интерфейсом [5].
Поэтому, запустив математический пакет Mathcad, достаточно ввести в привычном нам виде приведенные выше математические выражения (1)–(9), задав предварительно требуемые исходные данные: длину бревна, его диаметр в комле и в вершине, ширину фаски склеивания и толщину пропила. Листинг документа Mathcad, вычисляющего объем пустотелого бруса, состоящего из сегментов переменного сечения, представлен на рисунке 2.
Таким образом, изменяя значения исходных данных, сразу вычисляется объем пустотелого сырого бруса, значение которого можно использовать для дальнейших технологических и конструктивных расчетов.
Возможностями системы Mathcad целесообразно пользоваться и для нахождения математического описания поверхностей древесных материалов различной формы [6], что позволит не только получить графическую интерпретацию этих поверхностей, но и исследовать влияние отдельных факторов на свойства данных материалов.
Примером может служить работа по определению влияния асимметричной температуры плит пресса для управления конструкцией древесно-стружечных плит. При этом изучается зависимость величины покоробленности древесно-стружечных плит от температуры и температурной асимметрии на плитах с однородной и асимметричной конструкцией [10]. Полученные числовые значения покоробленности можно использовать для математического описания поверхности таких плит. Для этого воспользовались стандартным уравнением поверхности второго порядка:
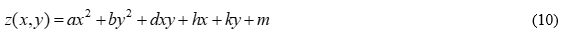
коэффициенты a, b, d, h, k, m которого находились путем решения системы линейных уравнений:
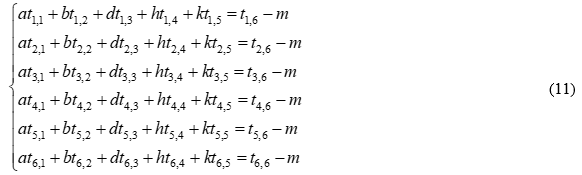
где ti,1, i = 1,2,…,6, – значение координаты x i-ой точки, возведенное в квадрат; ti,2 – значение координаты y i-ой точки, возведенное в квадрат; ti,3 – произведение координат x и y i-ой точки; ti,4 – значение координаты x i-ой точки; ti,5 – значение координаты y i-ой точки; ti,6 – значение координаты z i-ой точки. При этом точки характеризуют замеры покоробленности плиты в определенных местах для тех или иных условий прессования.

Рис. 2 – Листинг документа Mathcad для расчета объема пустотелого бруса
Решать подобные системы линейных уравнений также позволяет математический пакет Mathcad, предлагающий на выбор несколько методов: матричный, Гаусса или с помощью одной из функций – lsolve, Find или Minerr. На рисунке 3 представлен листинг документа Mathcad, отображающего нахождение решение системы линейных уравнений матричным способом и последующее получение уравнения соответствующей поверхности, описывающей покоробленность одной из исследуемых древесно-стружечных плит.

Рис. 3 – Листинг документа Mathcad для определения покоробленности плиты
Помимо этого, в Mathcad можно построить графическую интерпретацию полученного математического описания покоробленности этой древесно-стружечной плиты (см. рисунок 4).
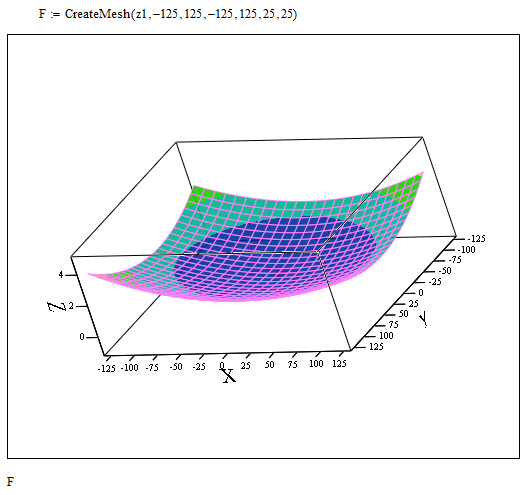
Рис. 4 – Поверхность, описывающая покоробленность плиты
Однако надо отметить, что применение Mathcad для решения исследовательских задач деревообработки не всегда оправдано. Это касается, в частности, задач, связанных, например, с построением виртуальной объемной модели бревна, позволяющей отображать внутреннюю структуру годичных слоев, а также их текстуру, получаемую при продольном раскрое бревна. Поскольку для решения подобных задач требуется как минимум написание полноценных программных алгоритмов, то в этом случае целесообразнее использовать математическую систему Matlab [1], [7], [9], которая, в отличие от Mathcad, предоставляет более широкие возможности для программирования с использованием достаточно развитого встроенного языка программирования, а также создания собственных приложений для моделирования и графической визуализации.
Заключение
Рассмотренные примеры использования пакета Mathcad показали эффективность его применения для решения исследовательских задач в области технологии деревообработки. Удобство интерфейса, широкие возможности данного математического пакета для обработки результатов научных исследований и их графической иллюстрации позволяют существенно сократить время обработки экспериментальных данных, полученных в ходе проведения различных исследований в деревообработке, а также избежать ошибок при осуществлении расчетов.
|
Конфликт интересов Не указан. |
Conflict of Interest None declared. |
Список литературы
Будовская Л.М. Введение в математические пакеты : учебное пособие / Л.М. Будовская, В.И. Тимонин. –Москва: МГТУ им. Н.Э. Баумана, 2018. –36 с.
Исаев С.П. Определение оптимальных размеров полого бруса квадратного сечения / С.П. Исаев // Композиционные материалы на основе древесины: тез. докл. международ. научно-техн. конф. –Москва : МГУЛ, 2000.–С. 67–68.
Пижурин, А.А. Исследования процессов деревообработки / А.А. Пижурин, М.С. Розенблит. –Москва : Лесн. Пром-сть, 1984. –232 с.
Сафин Р.Г. Основы научных исследований. Организация и планирование эксперимента : учебное пособие / Р.Г.Сафин, А.И. Иванов, Н.Ф. Тимербаев. –Казань: Изд-во КНИТУ, 2013. –156 с.
Кудрявцев Е.М. Mathcad11: Полное руководство по русской версии / Е.М. Кудрявцев. –Москва : ДМК Пресс, 2005. –592 с.
Макаров Е.Г. Инженерные расчеты в Mathcad15: Учебный курс / Е.Г. Макаров. –Санкт-Петербург : Питер, 2011.–400 с.
Дьяконов В.П. MATLAB7.*/R2006/R2007: Самоучитель / В.П.Дьяконов. –Москва : ДМК Пресс, 2008. –768 с.
Ануфриев И.Е. MATLAB7 / И.Е. Ануфриев, А.Б. Смирнов, Е.Н. Смирнова. –Санкт-Петербург : БХВ-Петербург, 2005. –1104 с.
Медведов В.Ю. Сравнительные характеристики пакетов Mathcad, Matlab, Mapleв применении крешению учебных математических задач / В.Ю. Медведов // Дни науки: материалы межвузовской научно-технической конференции студентов и курсантов на базе ФГБОУ ВО «Калининградский государственный технический университет» 8-21 апреля 2019 года. –Калининград: Изд-во КГТУ, 2019. –С. 439–444.
Плотников С.М. Исследование покоробленности древесностружечных плит с асимметричной структурой / С.М.Плотников // Известия вузов. Лесной журнал. –1989. –No 1. –С. 49–53.
