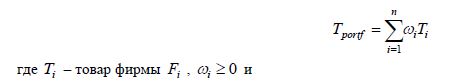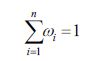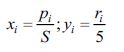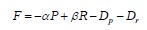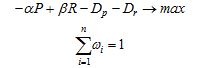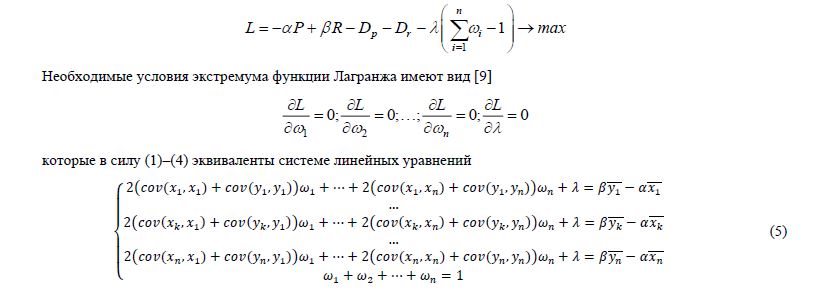ЭКОНОМИКО-МАТЕМАТИЧЕСКИЙ МЕТОД ОПТИМАЛЬНОГО ВЫБОРА ТОВАРА

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЙ МЕТОД ОПТИМАЛЬНОГО ВЫБОРА ТОВАРА

Научная статья

Звягинцев А.И.*

ORCID: 0000-0003-0199-6420,

Михайловская военная артиллерийская академия, Санкт-Петербург, Россия

* Корреспондирующий автор (azvyagintsev[at]mail.ru)

Аннотация

В статье предложен экономико-математический метод оптимального выбора товара с учетом критерия соотношения цены и качества товара. При разработке этого метода использован математический аппарат, включая теорию экстремальных задач и теорию вероятностей и математической статистики. Полученный метод удобен и эффективен в практическом использовании. Он применим как на бытовом, так и на производственном уровне, например при закупке предприятием комплектующих деталей, полуфабрикатов, приборов, компьютерной техники и т.д. Предлагаемый метод математически формализован в виде экстремальной задачи, решение которой сведено к алгебраической системе уравнений. В статье приведен конкретный пример практического применения разработанного метода.

Ключевые слова: товар, потребительский спрос, математические методы, оптимальный выбор.

ECONOMIC AND MATHEMATICAL METHOD OF OPTIMAL GOODS SELECTION

Research article

Zvyagintsev A.I.*

ORCID: 0000-0003-0199-6420

Mikhailovskaya Military Artillery Academy, Saint Petersburg, Russia

* Corresponding author (azvyagintsev[at]mail.ru)

Abstract

The article proposes an economic and mathematical method for the optimal choice of goods, taking into account the criterion of the balance of price and quality. When developing this method, a mathematical tool was used, including the theory of extremum problems and the theory of probability and mathematical statistics. The resulting method is convenient and effective in practical use. It is applicable both at the household and at the production level, for example, when an enterprise makes a purchase of components, semi-finished products, tools, computer equipment, etc. The proposed method is mathematically formalized in the form of an extremum problem, the solution of which is reduced to an algebraic system of equations. The article provides a concrete example of the practical application of the developed method.

Keywords: goods, consumer demand, mathematical methods, optimal choice.

Введение

В современной системе рыночных отношений потребитель является ключевым элементом. Каждый покупатель руководствуется полезностью товара, соотношением цены и качества, а также своими индивидуальными вкусами, отношением к моде, дизайну товаров и иными субъективными предпочтениями. Тема изучения потребительских предпочтений широко освещена в научных трудах, например в работах [1], [2], [3].

Теория потребительского поведения является одним из ключевых разделов микроэкономики. Одной из основных задач изучения поведения потребителя является исследование проблемы оптимального выбора потребительского товара физическими и юридическими лицами на рынках благ. При решении задачи оптимального выбора товара широко применяются математические методы, обзоры которых можно найти, например, в монографиях [4], [5], [6], [7]. Основные математические методы, используемые при принятии решений потребительского плана, базируются на классических методах теории экстремальных задач, методах линейного и нелинейного программирования, методах динамического программирования, игровых методах.

Актуальность темы данной статьи обусловлена тем фактором, что мы живем в мире бизнеса и рыночных отношений, в которых невозможно принимать оптимальные решения, не учитывая нюансы потребительского спроса, ведь именно потребитель, приобретая товар, в конечном итоге приносит прибыль предприятию, производящему товарную продукцию.

Основные результаты

В современных условиях огромного многообразия различных товаров покупатель сталкивается с задачей оптимального выбора нужного товара. Главными критериями выбора являются качество и цена товара. Будем рассматривать случай, когда юридическое или физическое лицо собирается приобрести конкретный товар, цена которого не выйдет за пределы определенного денежного лимита.

Пусть потребитель планирует купить товар Т, который производят n фирм 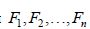 . При этом покупатель хочет, чтобы цена товара не превышала определенную денежную сумму S. Составим потребительский портфель

 

Качество товара можно оценить по результатам опроса пользователей или на основании экспертных оценок профессиональных специалистов (например, по пятибалльной шкале). Обычно для оценки качества используют рейтинг товара  . Многие крупные торговые сети на своих сайтах публикуют и регулярно обновляют рейтинги наиболее востребованных товаров.

Очень часто цены pi одного и того же товара отличаются в разных магазинах. В силу того, что цены и рейтинги подвержены частым изменениям, то с математической точки зрения pi  и ri являются случайными величинами.

Поскольку рейтинг и цена имеют разные размерности, то в целях приведения к одинаковой размерности будем рассматривать относительные показатели:

В результате такой нормировки случайные числа xi  и yi  изменяются в диапазоне от 0 до 1.

Для потребительского портфеля в качестве усреднения цены и рейтинга можно использовать математическое ожидание

Как правило, чем меньше разброс ценовых и рейтинговых показателей, тем выше потребительский спрос и ликвидность товара. Таким образом, Dp  и Dr являются косвенными показателями полезности товара.

Рассмотрим функцию полезности следующего вида:

где α, β – показатели потребительских предпочтений покупателя к цене и качеству, которые задаются дробными положительными числами (например, в долях или процентах).

Поскольку покупатель заинтересован в высоком качестве, низкой цене и максимальной полезности товара, то приходим к следующей задаче на условный максимум:

На компактном языке математики эта запись означает следующую экономическую интерпретацию. Оптимальный выбор покупателя формируется из n видов товара за счет поиска таких параметров wi , чтобы обеспечить наименьшую стоимость товара с приоритетом α и наивысшее качество с приоритетом β, сведя до максимума полезность товара.

Задача нахождения условного максимума сводится [9] к нахождению максимума функции Лагранжа

По теореме Кронекера–Капелли [10] эта система линейных уравнений совместна тогда и только тогда, когда ранг расширенной равен рангу матрицы системы. В частности, если определитель системы (5) отличен от нуля, то решение системы уравнений можно вычислить по формулам Крамера [10] или выразить в матричной форме:

 

В качестве примера практического применения полученного метода рассмотрим простой случай, когда некий гражданин решил купить новый смартфон по цене, не превышающей 30 тысяч рублей. Пусть для покупателя важнее всего качество, например качество в пять раз предпочтительнее чем цена, то есть α=0,01 и β=0,05. Предположим, что по составу технических опций и по дизайнерскому оформлению покупателю подходят три смартфона: «Honor 50 Lite 6+128GB», «HUAWEInova 8», «SamsungGalaxyM32 128GB». Для этих смартфонов на сайтах магазинов «М.Видео» [11], «DNS» [12], «Яндекс» [13] содержится текущая информация по ценам и рейтингам. Например, по состоянию на 29 мая 2022 года были следующие данные:

Таблица 1– Цены и рейтинги смартфонов

	Honor		HUAWEI		Samsung
	Цена, руб	Рейтинг	Цена, руб	Рейтинг	Цена, руб	Рейтинг
М.Видео	20 499	4,2	28 999	4,8	23 999	4,3
DNS	20 999	4,5	27 299	4,6	24 999	4,6
Яндекс	19 947	4,5	25 934	4,5	26 499	4,5

Примечание: источники – [11], [12], [13]

Разделив цены на 30000 и рейтинги на 5, получаем следующие нормированные статистические данные.

Таблица 2– Нормированные статистические данные

	X1	X2	X3	Y1	Y2	Y3
1	0,68	0,97	0,80	0,84	0,96	0,86
2	0,70	0,91	0,83	0,9	0,92	0,92
3	0,66	0,86	0,88	0,9	0,9	0,9

Используя стандартные формулы [8] для вероятностных характеристик дискретных случайных величин U и V

Заключение

Разработанный в данной статье экономико-математический метод удобен и эффективен при практическом использовании, поскольку в итоге он сводится к решению системы (5). После вычисления на основе статистических данных стандартных вероятностных характеристик и подстановки их в формулу (5) получается линейная алгебраическая система, решение которой не представляет труда. Полученный метод применим как на бытовом, так и на производственном уровне, например при закупке предприятием комплектующих деталей, полуфабрикатов, приборов, компьютерной техники и т.д. В случае большого значения n нужно использовать компьютерные пакеты программ, предназначенные для решения линейных алгебраических систем большой размерности с помощью приближенных методов. Например, для численного решения системы (5) можно использовать встроенную в Excel опцию «Поиск решения».

Конфликт интересов  Не указан.

Conflict of Interest  None declared.