СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ ИЗМЕНЕНИЯ СКОРОСТИ ОБУЧЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ В РАЗЛИЧНЫХ ЗАДАЧАХ КЛАССИФИКАЦИИ

СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ ИЗМЕНЕНИЯ СКОРОСТИ ОБУЧЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ В РАЗЛИЧНЫХ ЗАДАЧАХ КЛАССИФИКАЦИИ

Научная статья

Толстых А.А.¹, ^*, Голубинский А.Н.²

¹ Москва, Россия;

² АО «Концерн «Созвездие», Воронеж, Россия

^* Корреспондирующий автор (tolstykh.aa[at]yandex.ru)

Аннотация

В настоящее время искусственные нейронные сети (ИНС) успешно решают множество задач классификации, как бинарной, так и многоклассовой с различными типами информации в качестве входного вектора. Однако существует проблема эффективного обучения ИНС, так как для глубоких сетей алгоритмы оптимизации параметров второго порядка не применяются по причинам больших вычислительных затрат, используют различные вариации алгоритмов оптимизации первого порядка. Одной из основных проблем выбора алгоритма оптимизации является оценка его эффективности при обучении конкретной ИНС. В работе проведен анализ эффективности методов изменения скорости обучения искусственных нейронных сетей. Проанализированы различные подходы к изменению скорости обучения в процессе оптимизации параметров ИНС для различных задач классификации. Проанализировано влияние выбора метода оптимизации и количества параметров нейросетевого классификатора на эффективность обучения. Приведены экспериментальные результаты для двух различных задач классификации и их анализ. Результаты исследования могут быть применены при разработке нейросетевых классификаторов.

Ключевые слова: искусственные нейронные сети, обучение, методы оптимизации.

COMPARISON OF THE EFFECTIVENESS OF METHODS FOR CHANGING THE LEARNING RATE OF ARTIFICIAL NEURAL NETWORKS IN VARIOUS CLASSIFICATION TASKS

Research article

Tolstykh A.A.¹, ^*, Golubinsky A.N.²

¹ Moscow, Russia;

² JSC Concern «Sozvezdie», Voronezh, Russia

^* Corresponding author (tolstykh.aa[at]yandex.ru)

Abstract

Today, artificial neural networks (ANN) successfully solve many classification problems, both binary and multiclass ones, with various types of information as an input vector. However, there is a problem of effective training of ANN, since for deep webs, second-order parameter optimization algorithms are not used due to the reasons of high computational costs; variations of first-order optimization algorithms are used instead. One of the main problems of choosing an optimization algorithm is to evaluate its effectiveness in training a specific ANN. The paper analyzes the effectiveness of methods for changing the learning rate of artificial neural networks. Various approaches to changing the learning rate in the process of optimizing the parameters of the ANN for various classification tasks are examined. The influence of the optimization method choice and the number of parameters of the neural network classifier on the effectiveness of training is analyzed. Experimental results for two different classification tasks and their analysis are presented. The results of the study can be applied in the development of neural network classifiers.

Keywords: artificial neural networks, training, optimization methods.

Введение

Целью работы является проведение анализа эффективности алгоритмов оптимизации первого порядка для различных архитектур ИНС, полученных алгоритмом выбора количества нейронов [1], [2] при различных наборах входных данных.

Задачей исследования является проведение анализа эффективности оптимизации первого порядка для различных архитектур для формирования рекомендации по применению методов оптимизации в конкретных задачах классификации объектов на цифровых изображениях.

Одной из основных проблем, возникающих при построении классификаторов на основе сверточных нейронных сетей, является подбор параметров обучения [3], [4]. При неправильном выборе скорости обучения (СО) возрастает время обучения, вероятность попасть в локальный минимум функции ошибки и вероятность расхождения алгоритма обучения.

Методы изменения значения весов, в большинстве своем, основаны на идеях градиентного спуска по функции ошибки. Однако, в связи с тем, что размерность функции ошибки в ИНС может достигать десятков миллионов измерений, аналитическое вычисление градиентов является крайне трудной вычислительной задачей.

Обзор существующих методов изменения скорости обучения

Для решения поставленной задачи необходимо провести обзор существующих методов изменения скорости обучения при использовании методов обучения первого порядка. Существует множество способов оптимизации, позволяющих значительно снизить вычислительную сложность обучения, однако они увеличивают время нахождения оптимального решения и, в некоторых случаях, могут расходиться. Следует отметить, что СО явно входит во многие методы оптимизации функции ошибки. Методы оптимизации функции ошибки:

1. Градиентный спуск:

где, 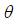– параметры сети;  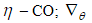 – градиент параметров сети; 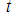– номер эпохи обучения.

2.Стохастический градиентный спуск:

где, i – случайно выбранный образец из обучающей выборки; N – количество обучающих образцов в выборке.

3. Momentum (может применяться как к обычному, так и к стохастическому градиентному спуску):

где, 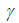– постоянная затухания.

4.Adagrad:

где, G – диагональная матрица, определяемая как 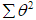 по всем предыдущим эпохам; 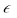– коэффициент регуляризации;  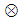– поэлементное перемножение матриц.

5. RMSprop:

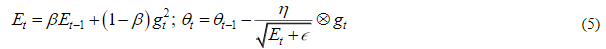
где, E  – накопительная переменная, содержащая квадраты предыдущих градиентов; 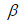  – коэффициент усреднения.

6. Adam [5]:

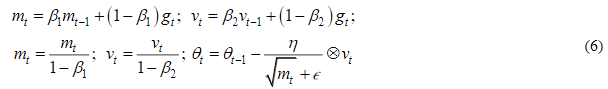
где, m – накопительная переменная, содержащая градиенты; 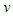–накопительная переменная, содержащая квадраты градиентов; 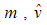– нормированные значения накопительных переменных.

Для относительно неглубоких ИНС целесообразно использовать методы оптимизации второго порядка. Наиболее распространенным методом является метод Левнберга-Марквардта [6]. Применение данного метода основано на использовании производных второго порядка, которые указывают направление глобального минимума. В данной статье не рассматривался, так как имеет большие вычислительные затраты (расчёт гессиана и якобиана). Более того, при увеличении количества параметров модели вероятность попасть в локальный минимум стремиться к нулю. Это следует из определения локального минимума, которое подразумевает увеличение функции ошибки во всех направлениях гиперпространства ошибки. Если распределение функции ошибки близко к нормальному, то вероятность попадания в локальный минимум стремиться к 0 (определение n несовместных событий вычисляется как ).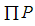

Существуют два вида СО: статическая и динамически изменяемая. На рисунке 1 представлена схема классификации СО.

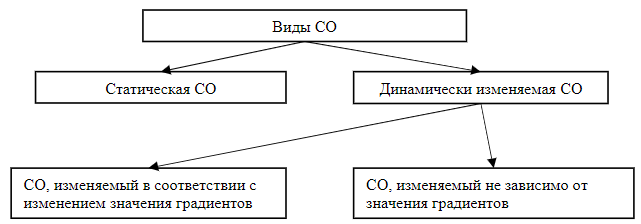
Рис. 1 – Классификация СО

Статическая СО определяется как константа и не меняется на протяжении всего времени обучения. Преимуществом подобного подхода является простота вычислений и малый объем занимаемой памяти. Однако при таком подходе достаточно трудно подобрать оптимальное значение СО, в связи, с чем время построения классификатора значительно возрастает. Динамический подход подразумевает коррекцию СО на каждой эпохе обучения. Наиболее интересным, с точки зрения автоматизации побора параметров обучения, является алгоритмический подход к изменению СО [7]. Для его использования необходимы вычислительные ресурсы, а также память, однако он сводит настройку СО к заданию начальных приближений.

В настоящее время выделяются 4 основные подхода к динамическому изменению СО.

1. Линейное уменьшение СО заключается в построении линейного множества коэффициентов от 1 до 0, содержащего коэффициент для каждой эпохи обучения. Таким образом, чем более поздняя эпоха обучения, тем на меньший коэффициент умножается приращение параметров искусственной нейронной сети. Применяя данный вид динамического изменения СО необходимо учитывать, что на последней эпохи обучения коэффициент приращения параметров будет равен нулю, таким образом, необходимо выбирать на 1 эпоху обучения больше, чем изначально запланировано.
2. Экспоненциальное уменьшение СО представляет собой модификацию линейного уменьшения СО, множество коэффициентов выбирается исходя из обратного экспоненциального закона.
3. Косинусное изменение СО основывается на идее использования в качестве закона выбора коэффициентов функции косинуса. Подобный выбор объясняется предположением, что на каком-то этапе обучения возможно попадание в локальный минимум и появление эффекта «паралича сети» [4]. Для того что бы эффективно выходить из локальных минимумов СО циклично увеличивается и уменьшается.
4. Изменение СО при «параличе сети» основан на постоянном измерении некоторой заданной метрики (например, целевой функции ошибки) и при отсутствии ее изменения более T эпох происходит снижение скорости СО. Данный способ является идейно противоположным косинусному изменению СО, так как при попадании в локальный минимум скорость не уменьшается, а увеличивается.

Рассмотрим используемые в работе параметры для каждого из шагов. Первоначальная инициализация является важной операцией, так как позволяет уменьшить вероятность возникновение таких проблем как «исчезновение градиентов» (vanishing gradient problem) для нейронов с нелинейной активацией и «смерть выпрямленных линейных функций» (dying ReLU), для нейронов с кусочно-линейной активацией [3]. Существует различные методы инициализации [3], [4]. В данной работе для первоначальной инициализации использовался метод Хи с нормальным распределением, в связи с его эффективностью в задачах классификации изображений [8]. Начальное значение генератора случайных чисел для генерации нормального распределения было фиксировано, для повторяемости формы распределения в каждой сессии обучения сверточных нейронной сети.

Значительное влияние на скорость обучения и точность классификатора оказывает выбор функции ошибки. Для бинарной классификации используется функция среднеквадратичной ошибки:

где 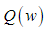 – функция ошибки; W – веса нейронов; N – количество образцов;  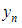 – истинный класс n-го образца;  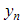– предсказанный классификатором класс n-го образца; a – матрица функций активации; X – обучающая выборка.

Функция ошибки, используемая для многоклассовый классификации, называемая перекрестная энтропия между классами, определяется следующим образом:

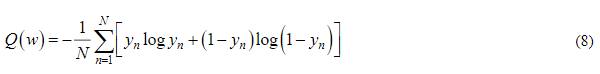
В работе рассматриваются алгоритмы оптимизации для моделей различных архитектур ИНС одного класса. Следует отметить, что алгоритмы RMSprop и Adam в своей сути используют метод взвешенного экспоненциального среднего, что подразумевает задание соответствующего окна усреднения. Для оценки размера окна усреднения используется следующая формула:

где L – размер окна усреднения; 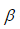 – параметр усреднения RMSprop или Adam. Таким образом, для рекомендуемых значений [4] градиенты усредняются на 10 и 1000 эпох. Для корректного сравнения эффективности алгоритмов целесообразно использовать число эпох значительно превосходящие размеры данных окон.

Основные результаты

В работе были использованы два различных набора данных: ирисы Фишера [9] и MNIST [10]. Для каждого из 3 способов изменения СО была проведена серия экспериментов (по 10 обучений с различных начальных инициализаций весов для каждой архитектуры, экспоненциальный способ не рассматривался, так как он не отличался от линейного), вопрос регуляризации сетей не рассматривался, использовался метод выбрасывания, метод нормализации мини-пакетов не применялся. В таблице 1 приведены исследуемые архитектуры ИНС, полученные алгоритмами выбора количества нейронов, предложенными авторами в [1], [2].

Таблица 1 – Исследуемые архитектуры ИНС

Архитектура	Количество параметров на задаче MNIST	Количество параметров на задаче Iris
Базовая	106506	11072
1 шаг алгоритма выбора	48928	3114
2 шаг алгоритма выбора	21404	787
3 шаг алгоритма выбора	7740	242
4 шаг алгоритма выбора	2860	92

Все вычисления происходили в одном окружении (как программном, так и аппаратном) для корректности сравнения результатов. В сессии экспериментов была зафиксирована метрика AUC, измерялось время обучения, необходимое ИНС для достижения значения данной метрики. Параметры обучения: количество объектов в мини-пакете, начальная СО были зафиксированы.

В качестве критерия выбора эффективности обучения выступало количество эпох, необходимых для достижения фиксированной метрики ROC AUC [4], которая была предварительно получена для всех архитектур, без применения дополнительного изменения СО. Данная базовая метрика составляет от 0,96 до 0,998 во всех задачах. Базовые классификаторы обучались 5000 и 1000 соответственно для задач Iris и MNIST.

Обсуждение

На рисунке 2 приведены графики обучения (по метрики AUC), усредненные по всем архитектурам.

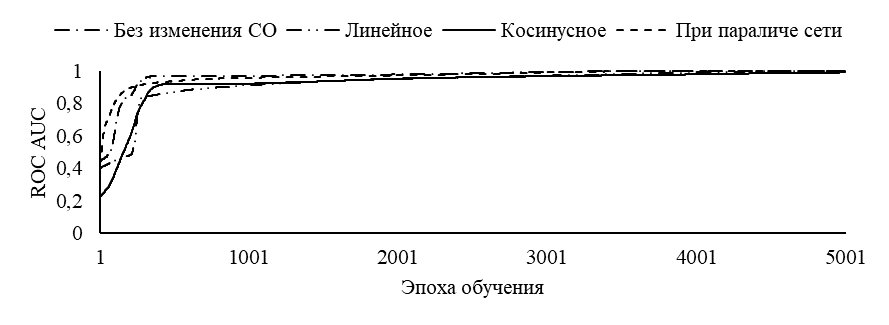
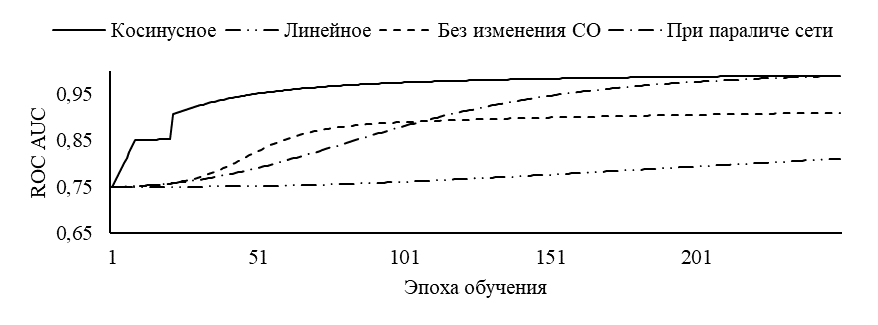
Рис. 2 – Графики истории обучения для метрики ROC AUC:
а – для задачи Iris; б – для задачи MNIST

Из рисунка 2 видно, что для относительно простых задач (Iris) способ изменения СО не дает значительных изменений скорости обучения. Однако, для более сложных задач (MNIST) наиболее предпочтительным является косинусный способ изменения СО. В таблице 2 приведены среднее по серии время обучения для каждой архитектуры.

Таблица 2 – Среднее по серии время обучения для каждой архитектуры

Метод изменения СО	Среднее количество эпох обучения (MNIST)	Среднее количество эпох обучения (Iris)
Без дополнительного изменения СО	1000	4600
Линейное уменьшение СО	550	4600
Косинусное изменение СО	150	4800
Изменение СО при «параличе сети»	250	4800

Заключение

В работе рассмотрены основные способы изменения СО, проанализированы результаты из применения в двух различных задачах классификации. Общие рекомендации заключаются в следующем:

• при простых архитектурах и задачах (низкой размерности входного пространства) нет необходимости использовать дополнительные способы изменения СО, достаточно стандартных оптимизаторов, с другой стороны, при сложных задачах и больших архитектурах предпочтительно использование косинусного изменения СО;
• при использовании глубоких свреточных сетей и высокой размерности входного пространства целесообразно использовать косинусное изменение СО, позволяющее избегать возникновения паралича сети при попадании в локальные минимумы;
• использование иных методов изменения СО целесообразно при достаточно большом бюджете времени на обучение, для более тонкой настройки параметров (весов) искусственной нейронной сети.

 

Конфликт интересов  Не указан.

Conflict of Interest  None declared.