РАСЧЕТ СЛОЖНЫХ СЕРПАНТИН УСОВЕРШЕНСТВОВАННЫМ МЕТОДОМ ПРОФЕССОРА ДУБЕЛИРА Г.Д.
РАСЧЕТ СЛОЖНЫХ СЕРПАНТИН УСОВЕРШЕНСТВОВАННЫМ МЕТОДОМ ПРОФЕССОРА ДУБЕЛИРА Г.Д.
Научная статья
Лопашук В.В.1, *, Лопашук А.В.2 , Лопашук С.В.3
1 ORCID: 0000-0003-2005-6055;
2 ORCID: 0000-0002-7823-3889;
3 ORCID: 0000-0002-5732-6242;
1, 2 Тихоокеанский государственный университет, Хабаровск, Россия;
3 ООО «Прогресс-ДВ», Хабаровск, Россия
* Корреспондирующий автор (VLopashuk[at]27pro.ru)
Аннотация
Расчет серпантин на автомобильных дорогах сводится к вычислению углов поворота вспомогательных закруглений. Если центр основного закругления расположен в точке пересечения ветвей, а вспомогательные закругления симметричные (простые серпантины) расчет выполняют по точным формулам. Простые серпантины встречаются очень редко. Смещая центр основного закругления серпантина становятся сложной. Для сложных серпантин известен только один точный метод расчета, описанный профессором Дубелиром Г.Д. Однако, предложенный им метод трудоемкий, использует четыре системы координат и применим только для серпантин первого рода с круговыми вспомогательными кривыми. Все это не позволило внедрить в практику проектирования метод Дубелира Г.Д. Серпантины просто конструируют, собирают из нескольких, независимых закруглений. В настоящей статье усовершенствован расчет серпантин по методу профессора Дубелира Г.Д.: предложено использовать прямоугольную и радиальную системы координат; получены точные формулы для расчета серпантин любого вида и рода; разработан единый алгоритм расчета. Обязательным условием применения предлагаемого метода является симметричность вспомогательных закруглений. Разработанный метод иллюстрирован примером расчета серпантины II рода.
Ключевые слова: Автомобильная дорога, закругление, серпантина, переходная кривая, угол поворота трассы, радиус круговой кривой, тангенс закругления.
CALCULATION OF COMPLEX SERPENTIN WITH THE IMPROVED METHOD OF PROFESSOR G.D. DUBELIR
Research article
Lopashuk V.V.1, *, Lopashuk A.V.2 , Lopashuk S.V.3
1 ORCID: 0000-0003-2005-6055;
2 ORCID: 0000-0002-7823-3889;
3 ORCID: 0000-0002-5732-6242;
1, 2 Pacific National University, Khabarovsk, Russia;
3 «Progress-DV» LLC, Khabarovsk, Russia
* Corresponding author (VLopashuk[at]27pro.ru)
Abstract
The calculation of serpentin on autoroads is reduced to the calculation of angular movements of auxiliary turns. If the center of the main turn is located at the intersection of the branches, and the auxiliary turns are symmetrical (simple serpentin), the calculation is performed in accordance to exact formulas. Simple serpentin is very rare. Shifting the center of the main turn of the serpentin becomes complicated. For complex serpentin, only one exact calculation method is known, described by Professor Dubelir G.D. However, the method proposed by him is laborious, uses four coordinate systems and is applicable only for serpentin of the first genus with circular auxiliary turns. All this did not allow the Dubelir G.D. method to be introduced into the design practice. Serpentin is simply constructed, assembled from several independent turns. In this article, the calculation of serpentin is improved by the method of Professor Dubelir G.D.: it is proposed to use rectangular and radial coordinate systems; exact formulas for calculating serpentin of any kind and genus are obtained; a unified calculation algorithm is developed. A prerequisite for the application of the proposed method is the symmetry of the auxiliary turns. The developed method is illustrated by an example of calculating a serpentin of the II genus.
Keywords: Highway, curving, serpentin, transition turn, the road rotation angle, the radius of the circular curve, the tangent of the curving.
Введение
При проектировании автомобильных дорог в горных условиях, преодолевая крутые подъемы, проектировщик удлиняет трассу, прокладывая ее под острым углом к горизонталям, зигзагами. Переломы проектной линии сопрягают несколькими закруглениями, описывающими острый угол перелома с внешней стороны. Такие комбинации закруглений называются серпантинами и они состоят из трех закругление и двух прямых вставок, расположенными между закруглениями (рис.1). Закругления могут быть не симметричными с переходными кривыми и круговой вставкой. Центр основного закругления располагается в любом месте, не обязательно в вершине угла поворота.
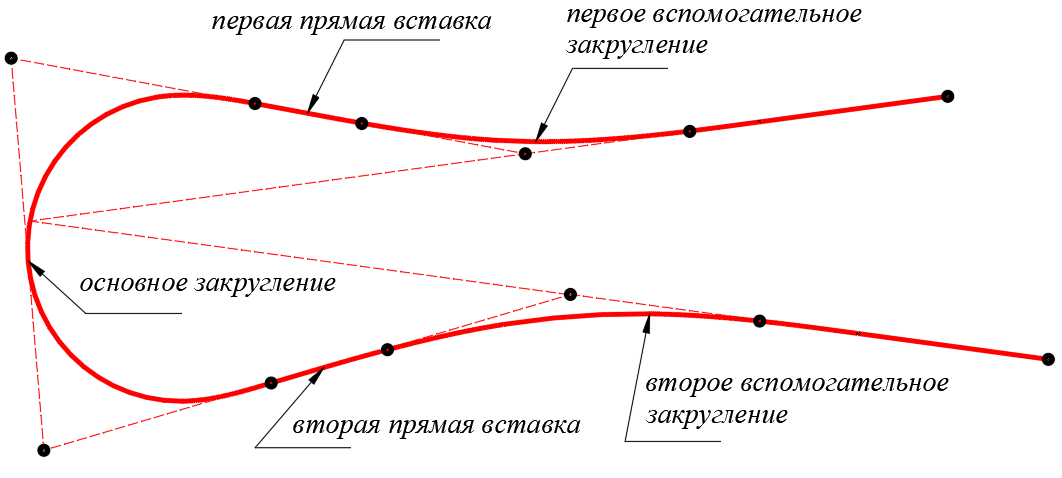
Рис.1 – Общий вид серпантины
Серпантина является сложным, состоящим в общем виде из 11 единичных элементов трассы: двух прямых, трех круговых кривых и шести клотоид, сопрягаемых между собой прямые и круговые кривые. В тоже время серпантину следует рассматривать как единый элемент, подчиняющейся закономерностям конфигурирования, когда, например, при изменении положения центра основного закругления меняется положение и конфигурация единичных элементов.
Расчетами серпантин занимались достаточно давно. Еще в справочнике инженера дорожника 1935 года [1] приведены понятия нормальных, упрощенных серпантин и площадок.
По всей сложности расчета серпантин, их можно разделить на две группы: простые (упрощенные), когда центр основного закругления находится в точке пересечения ветвей серпантины; сложные, когда центр основного закругления смещен в любом направлении относительно точки пересечения ветвей серпантины. Расчет любых серпантин сводится к вычислению углов поворота вспомогательных закруглений.
Формулы расчета углов поворота вспомогательных закруглений для простых серпантин достаточно просты, описаны многими авторами справочников, учебников и учебных пособий, позволяют однозначно вычислять углы, при условии, что вспомогательные закругления должны быть симметричными, т.е. иметь одинаковую длину переходных кривых в начале и в конце круговой вставки.
Сложные серпантины не имеют единого «подхода» к вычислению указанных углов поворота, и расчет углов сводится к решению математическими методами геометрических и тригонометрических задач.
В отечественной практике расчета сложных серпантин можно выделить три различных метода:
- описанный в учебнике «Основы проектирования автомобильных дорог» под редакцией профессора Дубелира Г.Д. за 1938 год [2];
- изложенный Седельниковым П.И. в «Руководстве по расчету и разбивке серпантин» в 1939 году [3];
- предложенный Митиным Н.А. в книге «Серпантины», изданной в 1972 и переизданной в 1980 годах [4].
Все другие авторы справочников, учебников и учебных пособий [5], [6], [8], [9] ссылаются на вышеуказанные методы, в основном на «Руководство по расчету и разбивке серпантин».
Проведенными исследованиями методов расчета сложных серпантин установлено:
- методы Седельникова П.И. и Митина Н.А. позволяют получать либо приближенные результаты, либо требуют корректировки параметров серпантин по результатам расчета углов поворота вспомогательных закруглений;
- метод расчета углов поворота вспомогательных закруглений, предложенный Дубелиром Г.Д. хотя, и является точным, однако ограничивается серпантинами I рода (вспомогательные закругления имеют кривизну разной направленности, см. рис.1) и отсутствием переходных кривых на вспомогательных закруглениях;
- ни один из выше описанных методов расчета, в том числе и простых серпантин, не позволяет проектировать серпантины с не симметричные вспомогательные закругления;
- авторами настоящей публикации предложен единый метод расчета и проектирования серпантин любого вида и рода [10], в том числе с не симметричными вспомогательными закруглениями.
Несмотря на наличие общего метода расчета серпантин [10], представляет интерес усовершенствовать метод Дубелира Г.Д. для получения методики расчета серпантин любого вида и рода.
Расчет серпантины I рода
Одним из недостатков методики расчета углов поворота вспомогательных кривых по методу Г.Д. Дубелира является применение двух систем координат для задания центра основного закругления: (X1 и Y1) для первого и (X2 и Y2) для второго вспомогательных закруглений. Устраним этот недостаток задав положение центра основного закругления в полярной системе координат, соответствующей общей расчетной схеме серпантины: через расстояние l и угол ω, отсчитываем против часовой стрелки начиная от биссектрисы острого угла серпантины α.
В этом случае для первого вспомогательного закругления (рис. 2) можно записать:
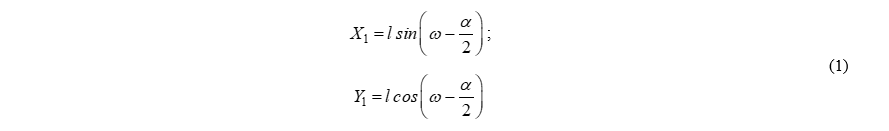
а для второго (рис. 3):
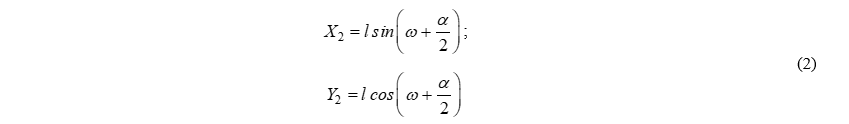
Остановимся в расчетах только на вычислении углов поворота вспомогательных закруглений (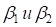 ), так как все последующие расчеты являются стандартными.
), так как все последующие расчеты являются стандартными.
Расчет выполним последовательно для первого и второго вспомогательных закруглений. Расчётная схема для определения угла 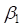 приведена на рис. 2. Рассматривая треугольники
приведена на рис. 2. Рассматривая треугольники 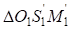 и
и 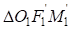 можно установить, что оба треугольника прямоугольные, имеют общую гипотенузу
можно установить, что оба треугольника прямоугольные, имеют общую гипотенузу 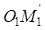 . Катеты первого треугольника
. Катеты первого треугольника 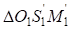 равны:
равны:
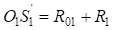 ;
;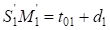 ,
,
где 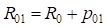 – радиус круговой кривой основного закругления (
– радиус круговой кривой основного закругления (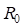 ) и сдвижка переходной кривой в начале основного закругления (
) и сдвижка переходной кривой в начале основного закругления (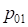 );
);
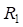 – радиус круговой кривой первого вспомогательного закругления;
– радиус круговой кривой первого вспомогательного закругления;
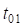 – тангенс переходной кривой в начале основного закругления;
– тангенс переходной кривой в начале основного закругления;
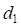 – прямая вставка между концом первого вспомогательного закругления и началом основного закругления.
– прямая вставка между концом первого вспомогательного закругления и началом основного закругления.
Катеты второго треугольника 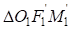 равны:
равны:
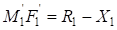 ;
; 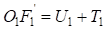 ,
,
где 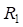 – радиус круговой кривой первого вспомогательного закругления;
– радиус круговой кривой первого вспомогательного закругления;
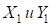 – ордината и абсцисса центра основного закругления в системе координат: центр в точке пересечения ветвей серпантины, абсцисса – по направления верхней ветви серпантины;
– ордината и абсцисса центра основного закругления в системе координат: центр в точке пересечения ветвей серпантины, абсцисса – по направления верхней ветви серпантины;
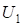 – проекция расстояние от центра основного закругления до ВУ1 на ось абсцисс;
– проекция расстояние от центра основного закругления до ВУ1 на ось абсцисс;
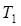 – тангенс круговой кривой первого вспомогательного закругления.
– тангенс круговой кривой первого вспомогательного закругления.
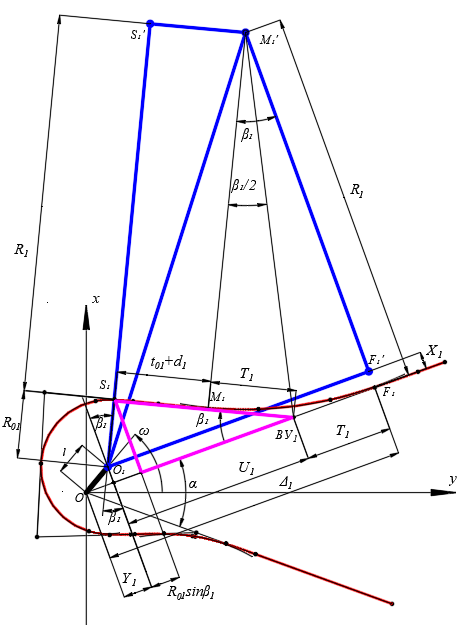
Рис. 2 – Расчетная схема серпантины I рода для определения угла поворота
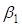 первого вспомогательного закругления
первого вспомогательного закругления
С учетом единства биссектрисы прямоугольных треугольников можно записать:
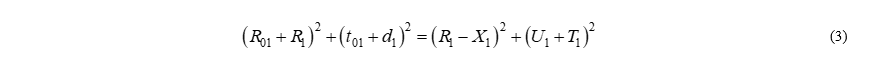
Обозначим через 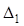 расстояние от центра пересечения ветвей серпантины до начала первого вспомогательного закругления, тогда:
расстояние от центра пересечения ветвей серпантины до начала первого вспомогательного закругления, тогда:
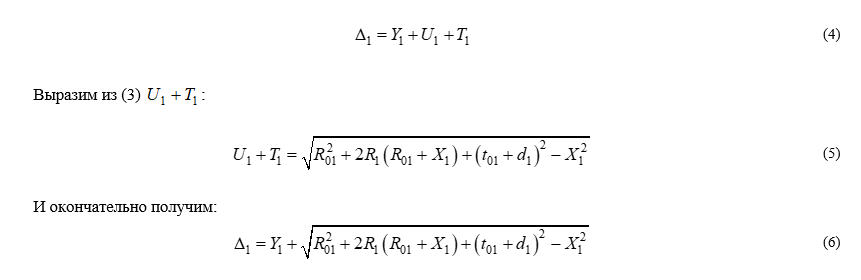 Из рис. 2 видно
Из рис. 2 видно
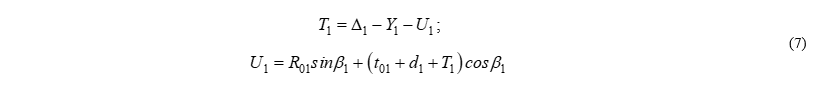 Подставим (
Подставим ( 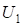 ) в выражение для (
) в выражение для ( 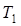 ) и группируя переменные получим:
) и группируя переменные получим:
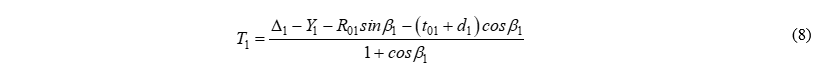 Применим тригонометрические формулы понижения степени и двойного угла:
Применим тригонометрические формулы понижения степени и двойного угла:
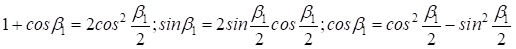
тогда:
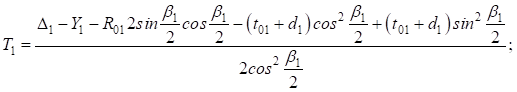
Или
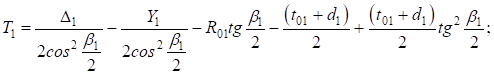
Заменив 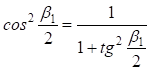 , подставив
, подставив 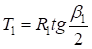 и сгруппировав переменные, получим квадратное уравнение:
и сгруппировав переменные, получим квадратное уравнение:
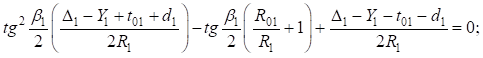
Упростим уравнения, введя новые обозначения: 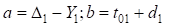 и разделив левую и правую части выражения на (
и разделив левую и правую части выражения на (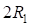 ), получим:
), получим:
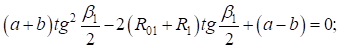
Найдем корни уравнения:
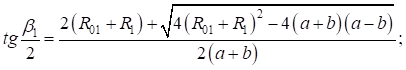
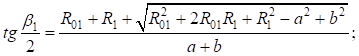
Принимая во внимание 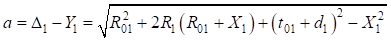 , получим:
, получим:
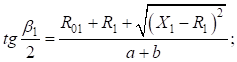
Окончательно формула приняла следующий вид:
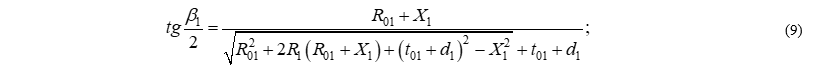
Расчётная схема для определения угла 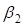 приведена на рис. 3. Рассматривая треугольники
приведена на рис. 3. Рассматривая треугольники 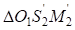 и
и 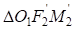 можно установить, что оба треугольника прямоугольные, имеют общую гипотенузу
можно установить, что оба треугольника прямоугольные, имеют общую гипотенузу 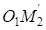 . Катеты первого треугольника
. Катеты первого треугольника 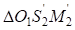 равны:
равны:
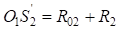 ;
; 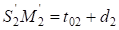 ,
,
где 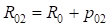 – радиус круговой кривой основного закругления (
– радиус круговой кривой основного закругления (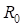 ) и сдвижка переходной кривой в конце основного закругления (
) и сдвижка переходной кривой в конце основного закругления (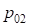 );
);
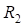 – радиус круговой кривой второго вспомогательного закругления;
– радиус круговой кривой второго вспомогательного закругления;
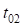 – тангенс переходной кривой в конце основного закругления;
– тангенс переходной кривой в конце основного закругления;
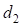 – прямая вставка между концом основного закругления и началом второго вспомогательного закругления.
– прямая вставка между концом основного закругления и началом второго вспомогательного закругления.
Катеты второго треугольника 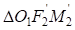 равны:
равны:
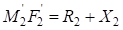 ;
; 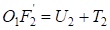 ,
,
где 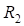 – радиус круговой кривой второго вспомогательного закругления;
– радиус круговой кривой второго вспомогательного закругления;
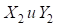 – ордината и абсцисса центра основного закругления в системе координат: центр в точке пересечения ветвей серпантины, абсцисса – по направления нижней ветви серпантины;
– ордината и абсцисса центра основного закругления в системе координат: центр в точке пересечения ветвей серпантины, абсцисса – по направления нижней ветви серпантины;
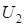 – проекция расстояние от центра основного закругления до ВУ2 на ось абсцисс;
– проекция расстояние от центра основного закругления до ВУ2 на ось абсцисс;
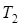 - тангенс круговой кривой второго вспомогательного закругления.
- тангенс круговой кривой второго вспомогательного закругления.
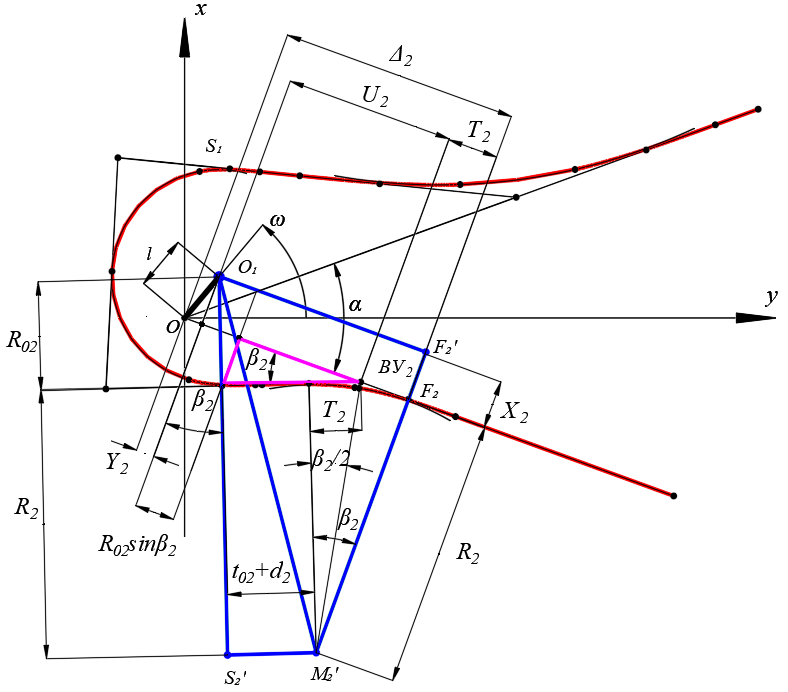
Рис. 3 – Расчетная схема серпантины I рода для определения угла поворота
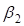 второго вспомогательного закругления
второго вспомогательного закругления
С учетом единства биссектрисы прямоугольных треугольников можно записать:
С учетом единства биссектрисы прямоугольных треугольников можно записать:
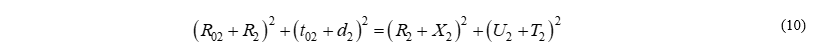
Обозначим через 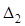 – расстояние от центра пересечения ветвей серпантины до начала второго вспомогательного закругления, тогда:
– расстояние от центра пересечения ветвей серпантины до начала второго вспомогательного закругления, тогда:
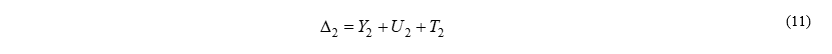
Выразим из (10) 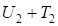 :
:
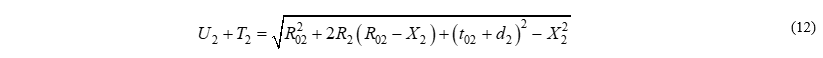
И окончательно получим:
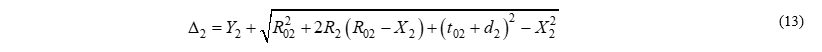 Из рис. 3 видно:
Из рис. 3 видно:
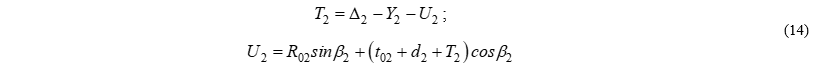 Подставим (
Подставим (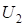 ) в выражение для (
) в выражение для (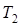 ) и группируя переменные получим:
) и группируя переменные получим:
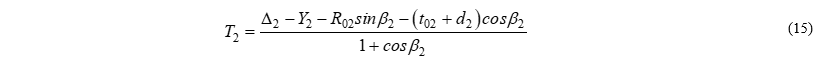
Применим тригонометрические формулы понижения степени и двойного угла:
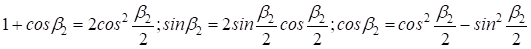
Тогда:
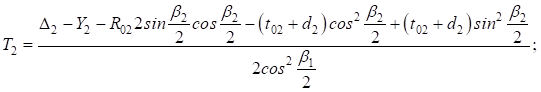
Или
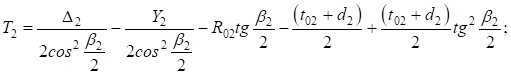
Заменив 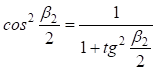 , подставив
, подставив 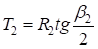 и сгруппировав переменные, получим квадратное уравнение:
и сгруппировав переменные, получим квадратное уравнение:
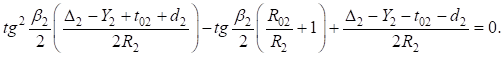
Упростим уравнения введя новые обозначения: 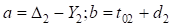 и разделив левую и правую части выражения на (
и разделив левую и правую части выражения на (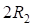 ), получим:
), получим:
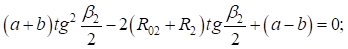
Найдем корни уравнения:
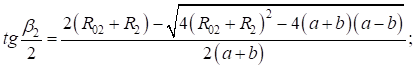
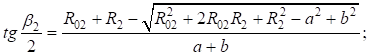
Принимая во внимание 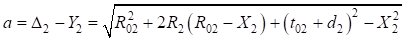 , получим:
, получим:
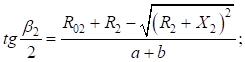
Окончательно формула приняла следующий вид:
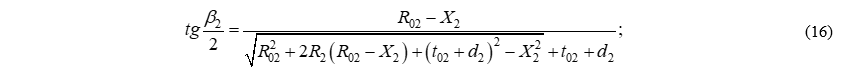
При выводе формул (9 и 16) было принято, что вспомогательные закругления не имеют переходных кривых. Однако указанное ограничение является избыточным. Для симметричных вспомогательных закруглений эти формулы можно с успехом применять. Для этого вместо величин (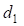 и
и 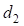 ) следует использовать (
) следует использовать (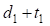 и
и 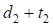 ), а вместо величин (
), а вместо величин (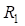 и
и 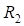 ) следует использовать (
) следует использовать (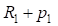 и
и 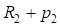 ), где (
), где (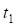 и
и 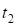 ) и (
) и (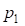 и
и 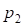 ) являются тангенсами переходных и сдвижками круговых кривых вспомогательных закруглений.
) являются тангенсами переходных и сдвижками круговых кривых вспомогательных закруглений.
Применим переменную (i) для обозначения номеров вспомогательных закруглений, можно предложить общую формулу для нахождения углов поворота вспомогательных закруглений серпантины I рода:
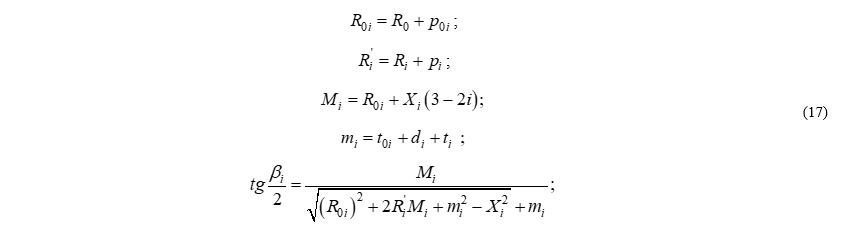
Расчет серпантины II рода
Расчет серпантины II рода выполним последовательно для первого и второго вспомогательных закруглений. Расчётная схема (рис.4) позволит определить угол 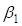 . Рассматривая треугольники
. Рассматривая треугольники 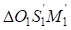 и
и 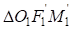 можно установить, что оба треугольника прямоугольные, имеющие общую гипотенузу
можно установить, что оба треугольника прямоугольные, имеющие общую гипотенузу 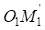 .
.
Катеты первого треугольника 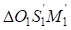 равны:
равны:
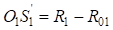 ;
; 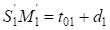 ,
,
где 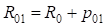 – радиус круговой кривой основного закругления (
– радиус круговой кривой основного закругления (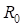 ) и сдвижка переходной кривой в конце основного закругления (
) и сдвижка переходной кривой в конце основного закругления (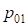 );
);
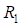 – радиус круговой кривой второго вспомогательного закругления;
– радиус круговой кривой второго вспомогательного закругления;
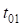 – тангенс переходной кривой в конце основного закругления;
– тангенс переходной кривой в конце основного закругления;
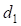 – прямая вставка между концом основного закругления и началом второго вспомогательного закругления.
– прямая вставка между концом основного закругления и началом второго вспомогательного закругления.
Катеты второго треугольника 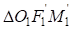 равны:
равны:
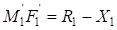 ;
; 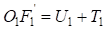 ,
,
где 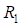 – радиус круговой кривой второго вспомогательного закругления;
– радиус круговой кривой второго вспомогательного закругления;
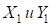 – ордината и абсцисса центра основного закругления в системе координат: центр в точке пересечения ветвей серпантины, абсцисса – по направления верхней ветви серпантины;
– ордината и абсцисса центра основного закругления в системе координат: центр в точке пересечения ветвей серпантины, абсцисса – по направления верхней ветви серпантины;
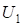 – проекция расстояние от центра основного закругления до ВУ1 на ось абсцисс;
– проекция расстояние от центра основного закругления до ВУ1 на ось абсцисс;
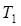 – тангенс круговой кривой первого вспомогательного закругления.
– тангенс круговой кривой первого вспомогательного закругления.
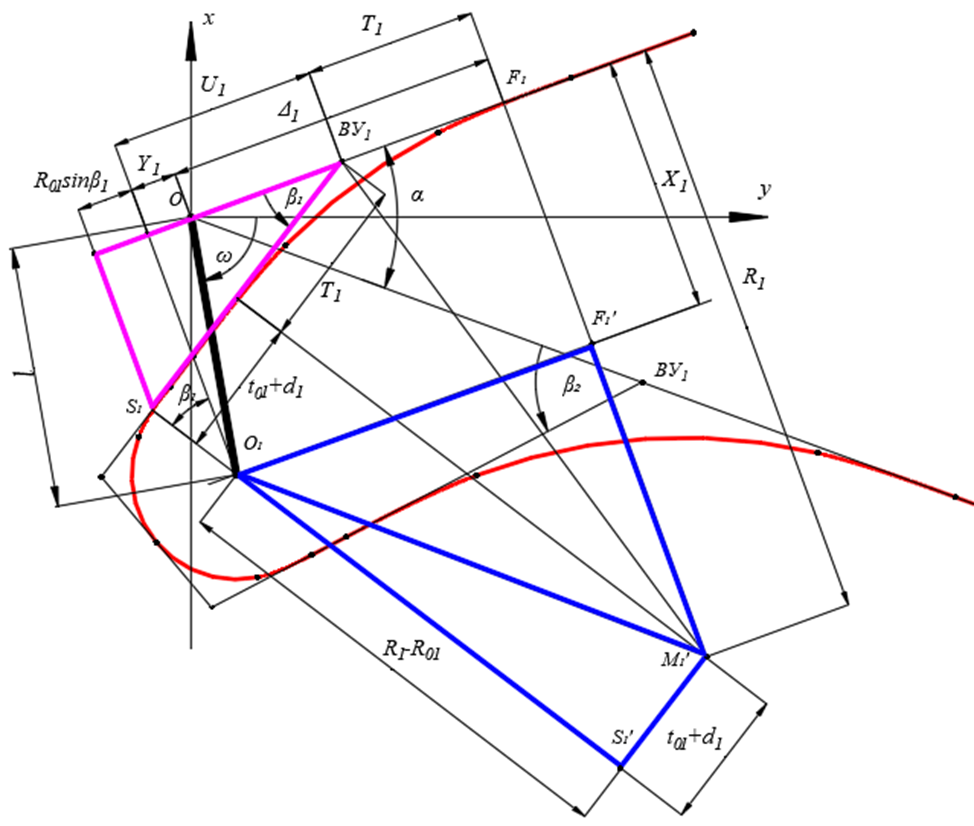
Рис. 4 – Расчетная схема серпантины II рода для определения угла поворота
С учетом единства биссектрисы прямоугольных треугольников можно записать:
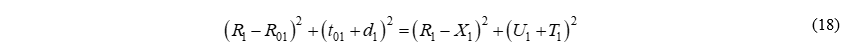 Обозначим через ∆1
Обозначим через ∆1 – расстояние от центра пересечения ветвей серпантины до начала первого вспомогательного закругления, тогда:
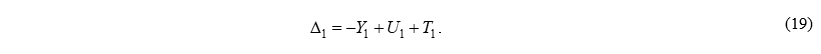 Выразим из (18)
Выразим из (18) 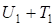 :
:
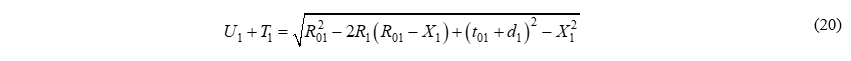 И окончательно получим:
И окончательно получим:
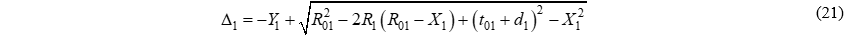
Из рис. 4 видно:
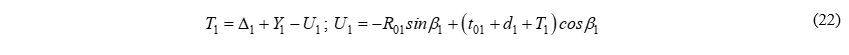 Подставим (U1) в выражение для (T1) и группируя переменные получим:
Подставим (U1) в выражение для (T1) и группируя переменные получим:
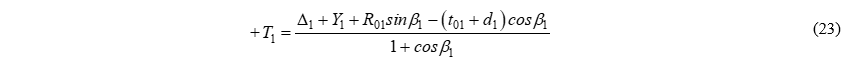 Применим тригонометрические формулы понижения степени и двойного угла:
Применим тригонометрические формулы понижения степени и двойного угла:
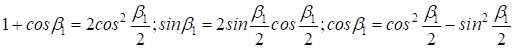
тогда:
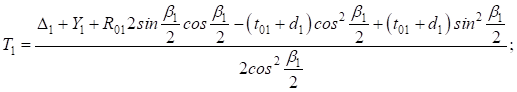
Или
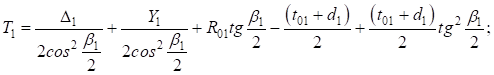
Заменив 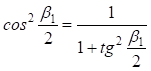 , подставив
, подставив 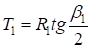 и сгруппировав переменные, получим квадратное уравнение:
и сгруппировав переменные, получим квадратное уравнение:
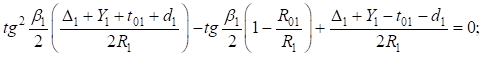
Упростим уравнения введя новые обозначения: 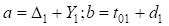 , – и разделив левую и правую части выражения на (
, – и разделив левую и правую части выражения на (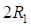 ), получим:
), получим:
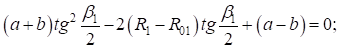
Найдем корни уравнения:
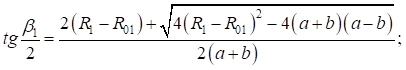
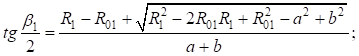
Принимая во внимание: 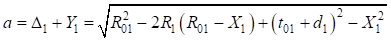 , – получим:
, – получим:
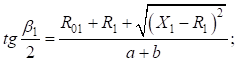
Окончательно формула для нахождения первого вспомогательного угла поворота серпантины II рода приняла следующий вид:
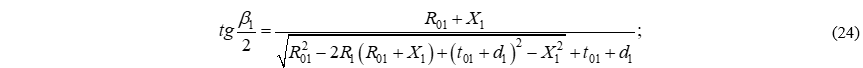
По аналогии получена формула для нахождения второго вспомогательного угла поворота серпантины II рода:
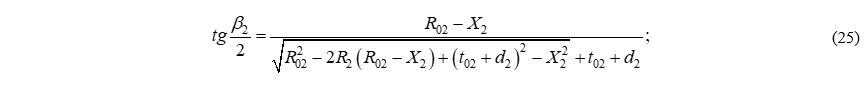
Сопоставляя формулы (9) и (16), а также (24) и (25) можно установить, что они попарно отличатся знаком части подкоренного выражения (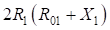 ) и (
) и (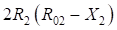 ). Для серпантин первого рода перед этими выражениями стоит знак (+), а для серпантин второго рода – знак (-).
). Для серпантин первого рода перед этими выражениями стоит знак (+), а для серпантин второго рода – знак (-).
Если использовать переменную (n), которая будет принимать значение (+1) серпантины I рода и (-1) серпантин II рода, а также применяя переменную (i) для обозначения номеров вспомогательных закруглений получим общую формулу для расчета углов поворота вспомогательных закруглений серпантины любого вида и рода:
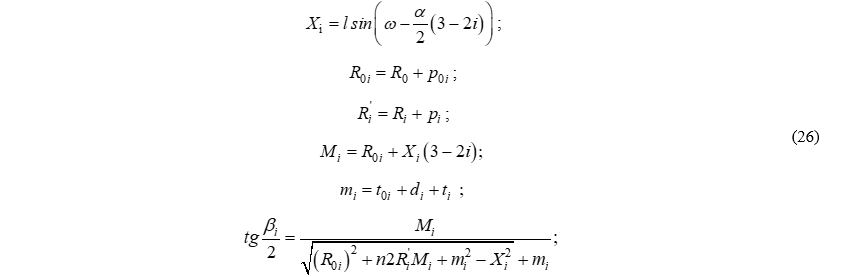
Как показали тестовые расчеты серпантин, если подкоренное выражение (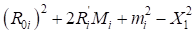 ) положительное, то угол (
) положительное, то угол (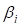 ) будет также положителен, что соответствует серпантине первого рода.
) будет также положителен, что соответствует серпантине первого рода.
Если подкоренное выражение (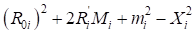 ) отрицательное, то следует принять (n= -1) и вычислить заново (
) отрицательное, то следует принять (n= -1) и вычислить заново (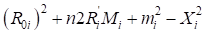 ). В этом случае угол (
). В этом случае угол (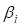 . ) будет также отрицательным, что соответствует серпантине второго рода.
. ) будет также отрицательным, что соответствует серпантине второго рода.
Если подкоренное выражение (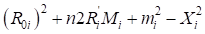 ) при любом значении (n) отрицательное, то рассчитать серпантину при заданных исходных данных не возможно. Этот случай имеет место при значительном удалении центра основного закругления от точки пересечения ветвей серпантины.
) при любом значении (n) отрицательное, то рассчитать серпантину при заданных исходных данных не возможно. Этот случай имеет место при значительном удалении центра основного закругления от точки пересечения ветвей серпантины.
Блок-схема алгоритма вычисления углов поворота вспомогательных закруглений с использованием уравнения (26) представлена на рис.5.
В частном случае простой серпантины (центр основного закругления находится в точке пересечения ветвей серпантины), величина (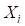 ) равна нулю и уравнение (26) преобразуется к простому виду (27):
) равна нулю и уравнение (26) преобразуется к простому виду (27):
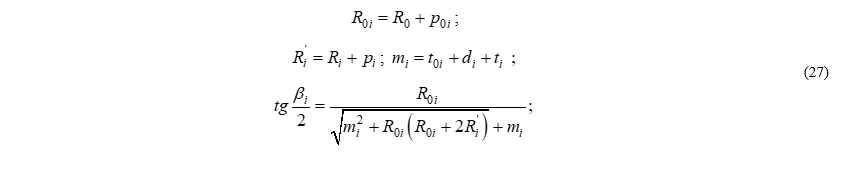
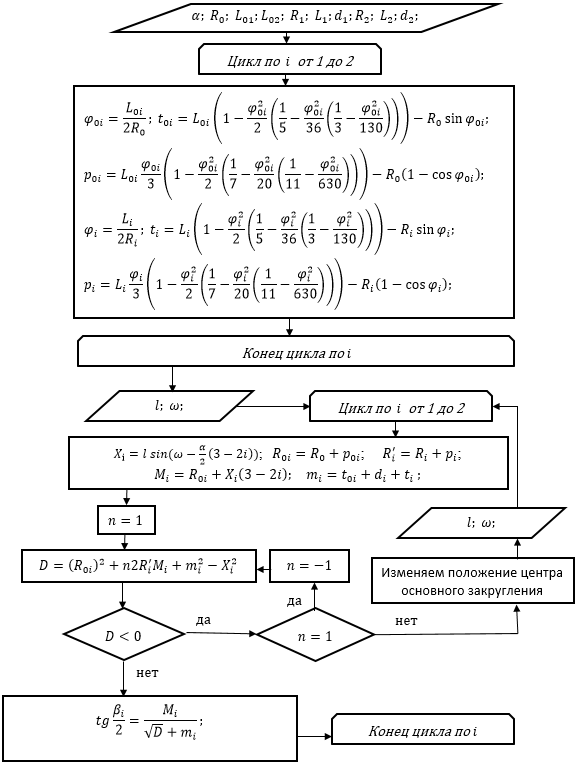
Рис. 5 – Блок-схема алгоритма вычисления углов поворота серпантин
с симметричными вспомогательными закруглениями
Пример расчета серпантины
Серпантина несимметричная второго рода с симметричными вспомогательными закруглениями.
Исходные данные:
Система координат прямоугольная, ось ординат направлена по биссектрисе острого угла серпантины, начало координат в точке пересечения ветвей серпантины. Для задания положения центра основного закругления используем полярную систему координат: ω=45о; l=250 м.
Основное закругление: R0=80 м; L01=45 м; L02=60 м;
Первое вспомогательное закругление: R1=250 м; L1=80 м; d1=20 м;
Второе вспомогательное закругление: R2=900 м; L2=120 м; d2=80 м;
Результат расчета:
Вычислим параметры переходных кривых основного и вспомогательных закруглений:
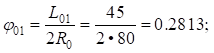
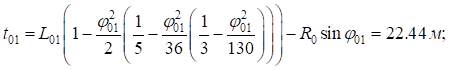
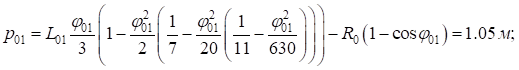
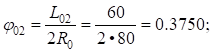
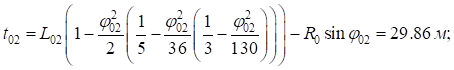
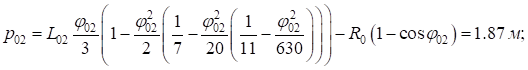
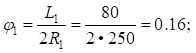
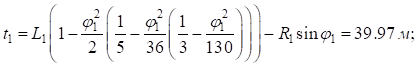
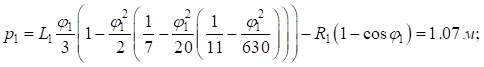
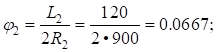
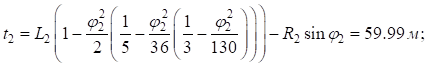
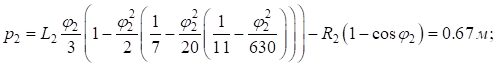
Расчет угла поворота первого вспомогательного закругления (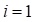 ):
):
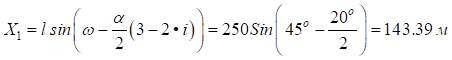 ;
;
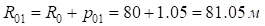 ;
;
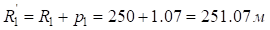 ;
;
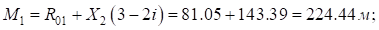
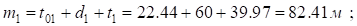
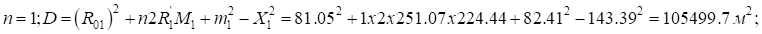
Так как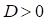 , определим:
, определим:
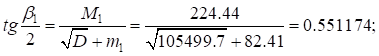
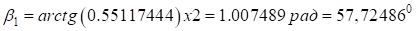 ;
;
Расчет угла поворота второго вспомогательного закругления (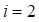 ):
):
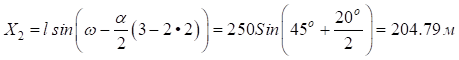 ;
;
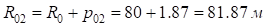 ;
;
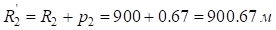 ;
;
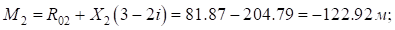
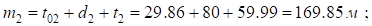
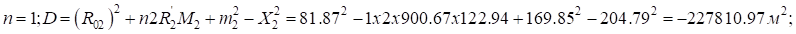
Так как 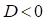 , изменим значение
, изменим значение 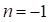 и определим
и определим 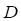 заново:
заново:
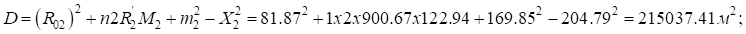
Так как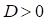 , определим:
, определим:
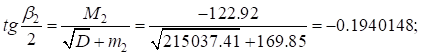
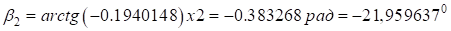 ;
;
Угол 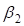 отрицательный, что является свидетельством серпантины второго рода. По результатам расчета построен план серпантинного участка трассы (рис.6).
отрицательный, что является свидетельством серпантины второго рода. По результатам расчета построен план серпантинного участка трассы (рис.6).
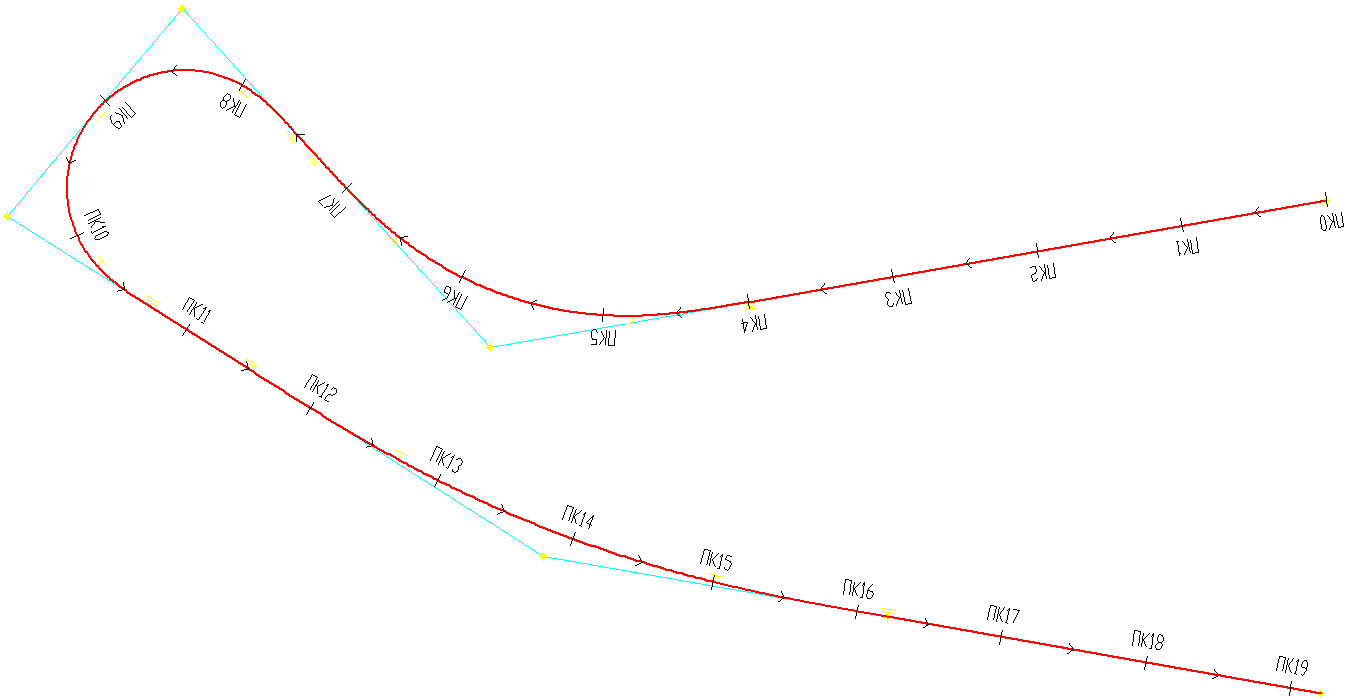
Рис. 6 – План серпантины II рода
Заключение
В результате проведенных исследований усовершенствован метод расчета серпантин, предложенный профессором Дубелиром Г.Д., разработан единый алгоритм выполнения расчетов серпантин любого вида и рода. Результат расчета серпантин апробирован на примере серпантины II рода.
Область применения предлагаемого метода расчета ограничивается следующими условиями:
- Вспомогательные закругления обязательно должны быть симметричными, иметь одинаковые длины клотоид в начале и в конце закругления;
- При выполнении расчетов может потребоваться изменение положение центра основного закругления, для получения согласованных результатов расчета.
|
Конфликт интересов Не указан. |
Conflict of Interest None declared. |
Список литературы
Справочник инженера дорожника для инженеров и техников дорожного дела. Изыскания и проектирование автогужевых дорог / Под ред. А.И.Анохина. – Ленинград : Государственное транспортное издательство, 1935. – 686 с.
Основы проектирования автомобильных дорог / Под ред.Г.Д.Дубелира. – Ленинград : Издательство Наркомхоза РСФСР. 1938. – 228 с.
Руководство по расчету и разбивке серпантин / Дор. н.-и. ин-т «ДорНИИ». – Москва : Гушосдор, 1939. – 128 с.
Митин Н.А. Серпантины. Метод расчета и разбивки. Таблицы / Н.А. Митин – Москва :Транспорт, 1980. – 213 с.
Справочник инженера-дорожника. Изыскания и проектирование автомобильных дорог / Под ред.О.В. Андреева. – Москва :Транспорт, 1977. – 559 с.
Бабков В.Ф. Проектирование автомобильных дорог: в 2-х ч. Ч.2 : учебник для вузов / В.Ф. Бабков, О.В. Андреев. – Москва : Транспорт, 1987. – 415 с.
Федотов Г.А. Изыскания и проектирование автомобильных дорог. В 2 кн. Кн.2: учебник / Г.А. Федотов, П.И. Поспелов. – Москва : Высш.шк., 2010. – 519 с.
Соколов М.Л. Изыскания и проектирование автомобильных дорог в горной местности / М.Л. Соколов, С.А. Трескинский – Москва. : Научно-техническое издательство министерства автомоб.транспорта и шоссейных дорог РСФСР, 1961. – 256 с.
Жуков В.И. Изыскания и проектирование автомобильных дорог в сложных условиях: учеб.пособие / В.И.Жуков, Т.В.Гавриленко. – Красноярск : Сиб.федер.ун-т, 2019. – 122 с.
Лопашук В.В. Единый метод расчета и проектирования серпантин / В.В. Лопашук, А.В. Лопашук, С.В. Лопашук // Вестник Евразийской науки. – 2020. – № 5.
