ТЕПЛООБМЕН МЕЖДУ СТРУЕЙ ПЛАЗМОТРОНА И НАГРЕВАЕМОЙ ПОВЕРХНОСТЬЮ РАСПЛАВА ГЛИНОЗЕМА ДЛЯ АЗОТА, АРГОНА И ВОДОРОДА

ТЕПЛООБМЕН МЕЖДУ СТРУЕЙ ПЛАЗМОТРОНА И НАГРЕВАЕМОЙ ПОВЕРХНОСТЬЮ РАСПЛАВА ГЛИНОЗЕМА ДЛЯ АЗОТА, АРГОНА И ВОДОРОДА

Научная статья

Кисон В.Э.^1, *, Мустафаев А.С.², Сухомлинов В.С.³

¹ ORCID: 0000-0001-9584-8474;

² ORCID: 0000-0003-2554-8526;

³ ORCID: 0000-0002-9986-4209;

^{1, 2} Санкт-Петербургский горный университет, Санкт-Петербург, Россия;

³ Санкт-Петербургский государственный университет, Санкт-Петербург, Россия

* Корреспондирующий автор (kison.vika[at]mail.ru)

Аннотация

В статье проведена оценка эффективности теплообмена между струей плазмотрона и нагреваемой поверхностью расплава глинозема с целью выбора оптимального рабочего газа для технологии производства чистого белого корунда. Данная технология разрабатывается с целью ее промышленного применения, с производительностью корунда 50 кг в час. По технологии кристаллы корунда получают путем расплавления порошка глинозема в реакторе струей плазмотрона. В качестве рабочего газа плазмотрона рассмотрены азот, аргон и водород. При расчетах использовались оценки теплофизических характеристик азота, аргона и водорода при рабочей температуре плазмотрона, то есть около 8000К. Были рассчитаны скорости струй и числа Нуссельта, характеризующие теплообмен, с учетом необходимой производительности. Согласно результатам расчетов, наиболее эффективный газ для нагревания и плавления глинозема – азот, ввиду его неполной диссоциации при рабочей температуре плазмотрона и, как следствие, более высокой теплопроводности и удельной энтальпии.

Ключевые слова: плазма, рабочий газ, плазмотрон, корунд.

HEAT EXCHANGE BETWEEN THE PLASMA TORCH JET AND THE HEATED SURFACE OF THE ALUMINA MELT FOR NITROGEN, ARGON AND HYDROGEN

Research article

Kison V.E.^1, *, Mustafaev A.S.², Sukhomlinov V.S.³

¹ ORCID: 0000-0001-9584-8474;

² ORCID: 0000-0003-2554-8526;

³ ORCID: 0000-0002-9986-4209;

^{1, 2} Saint Petersburg Mining University, Saint Petersburg, Russia;

³ Saint Petersburg State University, Saint Petersburg, Russia

* Corresponding author (kison.vika[at]mail.ru)

Abstract.

The article evaluates the efficiency of heat transfer between the plasma torch jet and the heated surface of the alumina melt in order to select the optimal working gas for the production technology of pure white corundum. This technology is being developed for the purpose of its industrial application with a corundum capacity of 50 kg per hour. According to this technology, corundum crystals are obtained by melting alumina powder in a reactor with a plasma torch jet. Nitrogen, argon, and hydrogen are considered as the working gas of the plasma torch. The calculations use estimates of the thermophysical characteristics of nitrogen, argon, and hydrogen at the operating temperature of the plasma torch, which approximately amounts to 8000K. The jet velocity and Nusselt numbers characterizing heat transfer were calculated taking into account the required performance. According to the results of calculations, the most effective gas for heating and melting alumina is nitrogen because of its incomplete dissociation at the operating temperature of the plasma torch and, as a result, higher thermal conductivity and specific enthalpy.

Keywords: plasma, working gas, plasma torch, corundum.

Введение

Технические системы в процессе развития усложняются, для их модернизации или разработки новых систем все чаще требуются материалы, обладающие особыми свойствами. Одним из таких материалов является синтетический корунд. Благодаря его абразивным свойствам, оптической прозрачности, химической, термической и радиационной стойкости он уже незаменим в электронной, оптической, авиационной и других отраслях промышленности и рынок только растет [1]. В связи с этим, возникает необходимость разработки промышленной технологии производства чистого белого корунда, так как существующие на данный момент способы получения оксида алюминия не применимы промышленно или не обеспечивают высокую чистоту материала [2]. Решением проблемы может стать плазменная технология с производительностью 40-50 кг чистого корунда в час, для достижения производительности сравнимой с существующими промышленными способами.

При разработке технологий плазменной плавки материалов неизбежно встает вопрос ее эффективности и энергопотребления. Эффективность переноса тепла при плазменной плавке определяется, в том числе, и эффективностью теплообмена между плазменной струей и нагреваемой поверхностью.

При взаимодействии струи со свободной поверхностью жидкой или твердой фазы поток испытывает торможение (при больших скоростях – адиабатическое), что следует учитывать при расчете теплопереноса.

Теплообмен между плазмой и расплавом через пятно в окрестности точки торможения потока плазмы можно оценить с использованием числа Нуссельта (Nu) и закона Фурье [3]

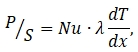    (1)

где P – передаваемая тепловая мощность,

S – площадь пятна разогрева,

λ – теплопроводность рабочего газа,

– градиент температуры в окрестности точки торможения.

Число Нуссельта, в свою очередь, зависит от чисел Рэлея (Ra), Рейнольдса (Re) и Прандтля (Pr). Эта связь определяется типом конвекции (вынужденная или естественная), типом течения (пленочное, ламинарное или турбулентное, дозвуковое или сверхзвуковое) и т.п. [4].

Струю плазмотрона можно считать практически равновесной [5], [6]. Будем также считать, что состав атмосферы над поверхностью совпадает с составом рабочего газа плазмотрона. Тогда можно воспользоваться известным решением задачи о "затопленной струе", которая дает пространственные распределения газовых параметров при истечении струи через отверстие в покоящийся собственный газ [7]. Расчеты показывают, что в рассматриваемых условиях струя плазмотрона является турбулентной, а тип конвективного переноса тепла - вынужденный.

При оценке числа Нуссельта для конкретных условий необходимо иметь ввиду, что оно меняется по сечению струи из-за изменений параметров самой струи (чисел Рейнольдса, Прандтля и т.д.). Согласно результатам расчетов, проведенных авторами [8] и экспериментальным данным [9] по радиальному распределению давления в окрестностях точки торможения турбулентной газовой струи при ее взаимодействии с плоской поверхностью, можно заключить, что на радиусе давление спадает более чем на порядок, при этом наблюдается слабая зависимость от числа Рейнольдса. Само же число Нуссельта на радиусе струи падает приблизительно в три раза. Это необходимо учитывать при оценке эффективности теплообмена между струей плазмотрона и нагреваемой поверхностью.

Реализуемый при технологии плазменного плавления глинозема режим соответствует взаимодействию «горячей» турбулентной струи с «холодной» плоской поверхностью при относительно больших числах Рейнольдса (порядка 10⁴ [10]). Определения «горячий» и «холодный» здесь и далее употребляются для сравнения температур пары тел относительно друг друга, как «имеющий большую/меньшую температуру». Для рассматриваемого режима связь чисел  имеет вид [11]:

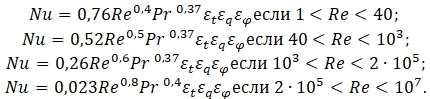    (2)

Здесь

- поправка, учитывающая зависимость физических свойств текучей среды от температуры,

 - поправка, учитывающая сужение потока в самом узком сечении канала,

 - поправка, учитывающая влияние угла  на коэффициент теплоотдачи;

 - числа Прандтля при температуре потока и стенки, соответственно;

d, H – кривизна поверхности и характерный поперечный размер течения;

φ – угол, который составляет массовая скорость на оси струи с касательной к поверхности. То есть, в случае нормального падения выполняется  Для оценки чисел  использовались известные соотношения [12]:

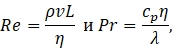   (3)

где η - динамическая вязкость газа; c_p - удельная теплоемкость среды при постоянном давлении.

При расчетах чисел Рейнольдса и Прандтля для молекулярных газов при высокой температуре необходимо учитывать, что их физические свойства с ее ростом существенно изменяются и отклоняются от значений, характерных для одноатомных газов. Это происходит в результате частичной диссоциации молекул при высоких температурах. Так, теплоемкость аргона при постоянном давлении практически не зависит от температуры. Удельные же теплоемкости азота и водорода, напротив, существенно возрастают при увеличении температуры [13], причем изменение составляет десятки процентов. Это следует из данных, приведенных на рисунках 1 и 2, на которых представлены теплоемкости водорода и азота в широком диапазоне температур.

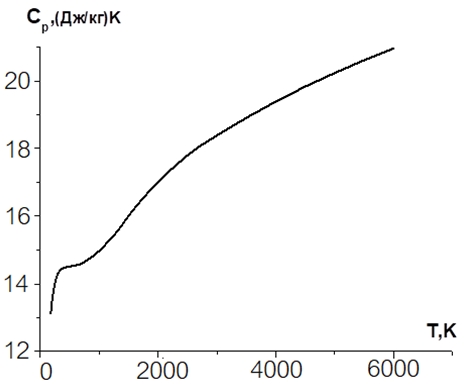
Рис. 1 – Удельная теплоемкость водорода как функция температуры

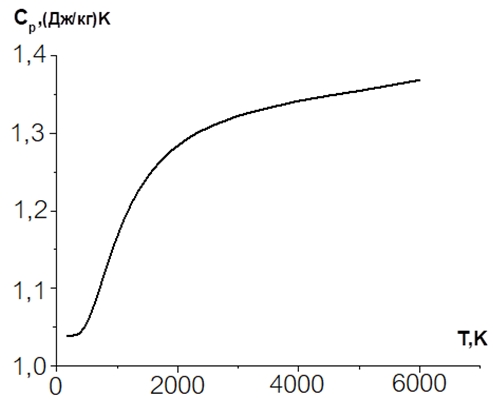
Рис. 2 – Удельная теплоемкость азота как функция температуры

 

В расчете также понадобятся данные об удельной энтальпии (h) выбранных газов от температуры в широком диапазоне. Согласно [14], зависимость энтальпии аргона от температуры можно условно считать линейной. Это не имеет места для молекулярных газов водород и азот, поскольку они диссоциируют при температурах выше 2500 К и 5000 К, соответственно. Водород при температуре выше 5000 К становится практически атомным газом, а к 8000К степень диссоциации равна 0,999, поэтому его энтальпия от 5000К растет линейно. Степень диссоциации азота при 5000 К равна 0,26, что существенно меньше, чем у водорода из-за разницы энергий диссоциации, поэтому при рабочей температуре 8000 К заметная часть азота будет все еще находиться в молекулярном состоянии.

Важная проблема эксплуатации реакторов с применением газовой плазмы при высоких температурах – накопление атомов этих газов в приповерхностных слоях за счет абсорбции и дальнейшей диффузии внутрь материала стенок. Эти процессы приводят к изменениям физико-химических свойств поверхности стенок реактора (как правило, к уменьшению теплопроводности и механической прочности, увеличению хрупкости и т.п.). В отличие от азота, водород на поверхности, как правило, диссоциирует на атомы. Вследствие этого адсорбция молекулярного азота приводит к заметно меньшим диффузионным потокам вглубь материала стенок, чем атомарного водорода, из-за сильно различающихся коэффициентов диффузии [15]. Таким образом, накопление поглощенного газа в случае азота происходит существенно медленнее, чем для водорода.

Итак, после рассмотрения температурных зависимостей теплофизических характеристик выбранных газов, можно оценить величины чисел Нуссельта  при применении качестве рабочего газа плазмотрона аргона, водорода и азота, соответственно. Для этого, как следует из соотношений (2), необходимо вычислить соответствующие числа Рейнольдса и Прандтля. Они, в свою очередь, кроме теплофизических характеристик, зависят от скорости струи на выходе из плазмотрона.

Скорость струи на выходе из плазмотрона зависит от требуемой производительности установки. Как было сказано во введении, целью является оценка возможности применения плазмотрона для производства 50 кг белого корунда в час. Соответственно, для производства 50 кг в час белого корунда необходимо расплавлять 50 кг в час глинозема. Требуемую для этого мощность находилась из разности энтальпии твердого и расплавленного глинозема, имея виду, что эту энергию нужно выработать за 1 час:

При были использованы значения удельных энтальпий [13]:

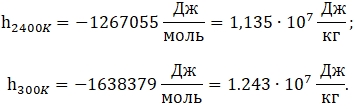
Для оценки скорости истечения струи из плазмотрона принято, что к.п.д. плазмотрона  [16]. При этом струя при взаимодействии с поверхностью остывает от температуры  до температуры  (температура получаемого расплава). Таким образом, мощность, передаваемая поверхности  равна:

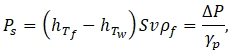   (4)

 

где величины с индексом  вычисляются при температуре струи, с индексом  - при температуре поверхности. Отсюда оценка для скорости истечения газа на срезе выходного сопла плазмотрона

   (5)

Оценки скорости разных газов по формуле  (5) с использованием вышеприведенных данных о теплофизических константах газов в предположении, что  (типичное значение для плазмотрона мощностью порядка 50-100 кВт), что соответствует радиусу струи 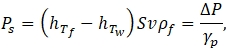, дают следующие результаты

    (6)

Для чисел Прандтля всех трех газов с использованием данных об их физических характеристиках получаем . Соответственно, для чисел Рейнольдса течений газа имеем для рассматриваемых условий: 

Наконец, расчет чисел Нуссельта по соотношениям (2) дает

     (7)

Отметим, что экспериментальные данные [17], [18] для близких к рассматриваемым условиям дают величину числа Нуссельта для аргона , что хорошо согласуется с полученной оценкой.

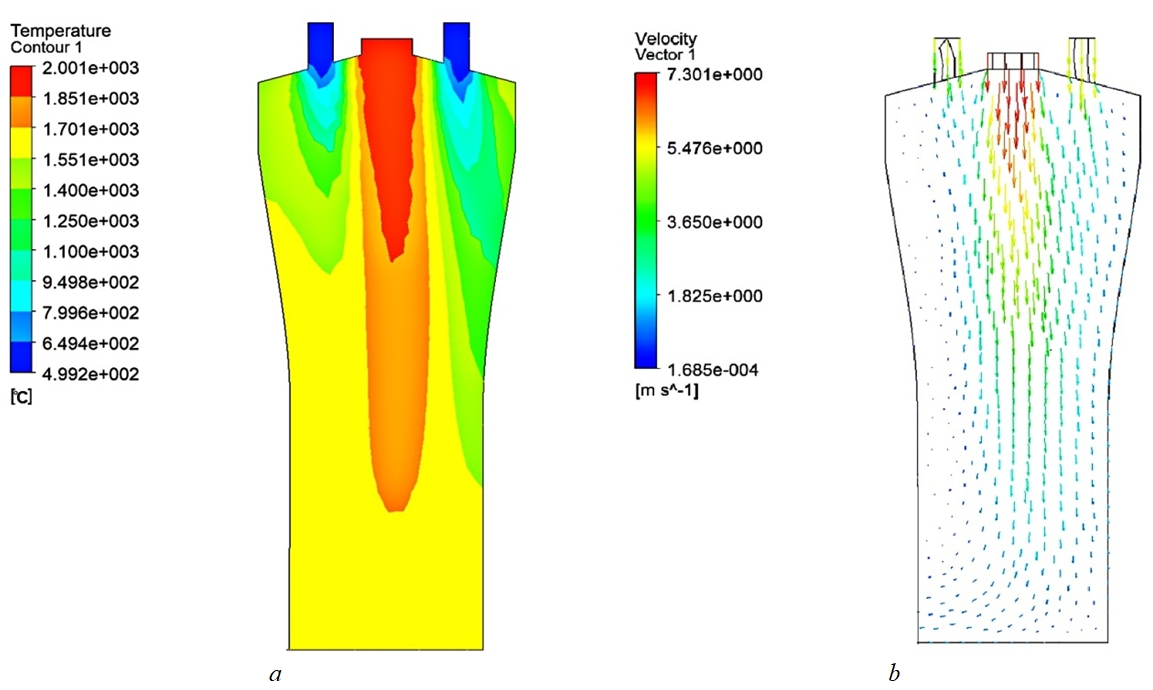
С помощью специализированного программного CAD-пакета SpaceClaim (продукт компании ANSYS) была получена упрощенная осесимметричная модель плазмотрона. Результаты моделирования процесса истечения плазменной струи приведены на рис. 3, где слева показано распределение температуры по струе, а сплава распределение скоростей.

Рис. 3 – Результат моделирования процесса истечения плазменной струи из плазмотрона:

a – распределение температур; b – распределение скоростей

Теперь можно оценить подводимую мощность с использованием соотношения (1). Для оценки, положим . Необходимо также вычислить величину . Это можно сделать, оценивая толщину пограничного теплового слоя течения .

Толщина динамического погранслоя δ (области течения, где массовая скорость меняется от значения скорости невозмущенного потока до нуля на обтекаемой поверхности) и толщина теплового погранслоя  (области течения, где температура меняется от соответствующей невозмущенному течению до температуры , соответствующей поверхности ) при дозвуковом течении связаны соотношением [19]:

   (8)

Как показано выше, в рассматриваемых условиях выполняется . Таким образом, толщину теплового слоя можно оценить, оценивая толщину динамического слоя, поскольку . Для этого можно использовать соотношение [20]:

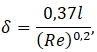    (9) где  Формула (9) является оценкой сверху для величины . Таким образом, для : Тогда поверхностная плотность мощности:  

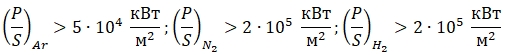
Согласно данным [8], [9], число Нуссельта спадает на радиусе струи приблизительно в два с половиной - три раза и среднее его значение по пятну контакта поверхности с струей плазмотрона примерно в 2 раза ниже, чем в центре пятна. Тогда для оценки снизу подводимой мощности получаем при площади пятна нагрева  и скоростях потока на срезе сопла плазмотрона, определенных соотношениями (6): 

То есть, расчетные режимы плазмотрона для азота и водорода с энергетической точки зрения способны обеспечить планируемый выход белого корунда в 50 кг в час с площадью пятна контакта струи с расплавом, даже равной площади выходного отверстия. Что касается аргона, то для него необходимо увеличение площади пятна контакта минимум в два раза. Реально, за счет расширения струи плазмы от выходного отверстия плазмотрона до поверхности расплава требуемое увеличение существенно меньше и может быть обеспеченно небольшим отклонением струи от нормали к поверхности. 

Заключение

Таким образом, как и ожидалось, получено, что рабочие газы азот и водород более эффективны с точки зрения нагрева и дальнейшего плавления глинозема, чем аргон. Физическая причина этого – более высокая теплопроводность и удельная энтальпия молекулярных газов при высоких температурах, обусловленные диссоциацией молекул этих газов на атомы. Тем не менее, необходимо отметить различие в параметрах плазмотрона в случаях использования азота и водорода в качестве рабочих газов.

Как видно из приведенных выше данных, при одинаковой подводимой к расплаву энергии, скорость струи у плазмотрона на азоте может быть существенно (почти на порядок) ниже, чем у плазмотрона на водороде и в пять-шесть раз ниже, чем у плазмотрона на аргоне. Причиной этого является низкая плотность водорода по сравнению с азотом при примерно одинаковой их удельной энтальпии.

Кроме того, использование водорода менее предпочтительно по причине его быстрого накопления материалом первого слоя тепловой защиты и изменения вследствие этого его физико – химических характеристик.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Рыбкина Е.А. Рынок синтезированных монокристаллов (сапфиров): реалии и перспективы / Е.А. Рыбкина // Инновации №9 (215), 2016, с. 106-110
2. Попова А.Н. Новые плазменные технологии в материаловедении и металлургии / А.Н. Попова, В.Э. Кисон, А.С. Мустафаев, В.С. Сухомлинов // Нанофизика и наноматериалы. Сборник научных трудов семинара 2020, Санкт-Петербург, с. 282-285
3. Boulos M.I. Fundamentals of plasma particle momentum and heat transfer /I. Boulos, P. Fauchais, A. Fardelle et al. // Plasma Spraying: Theory and Applications 1993, pp. 3-57.
4. Михеев М.А. Основы теплопередачи / М.А. Михеев. - М. - Л.: ГЭИ, 1956. - 390 с.
5. Жуков М.Ф. Электродуговые генераторы термической плазмы / М.Ф. Жуков, И.М. Засыпкин, А.Н. Тимошевский и др. - Новосибирск: Наука. Сиб. предпр. РАН, 1999 – 712с.
6. Энгельшт В.С. Теория столба электрической дуги / В.С. Энгельшт, В.Ц. Гурович, Г.А. Десятков и др. - Новосибирск: Наука, 1990. – 375c.
7. Ландау Л.Д. Гидродинамика. Теоретическая физика: т. VI / Л.Д. Ландау, Е.М. Лифшиц. 3-е изд., -М. :Наука. Гл. ред. физ - мат. лит.,1986, - 736с.
8. Бухмиров В.В. Расчет коэффициента конвективной теплоотдачи (основные критериальные уравнения): метод. указ. [Электронный ресурс] / Бухмиров В.В., Ивановский государственный энергетический университет им. Ленина, Иваново, 2007. – 39с. URL: https://clck.ru/VsGNy (дата обращения 15.04.2021)
9. Aihara T. Effects of temperature-dependent fluid properties on heat transfer due to an axisymmetric impinging gas jet normal to a flat surface / T. Aihara, J.K. Kim, and S. Maruyama // Waerme - und Stofffibertragung 25 (1990), Sendai, Japan, 145-153 (1990) DOI: 10.1007/BF01590145
10. Корсунов К.А Расчет параметров электродуговой плазмы в канале плазмотрона. / К.А. Корсунков // Успехи прикладной физики 2013 №6. (т.1), с.724-733
11. Галин Н.М. Тепломассообмен (в ядерной энергетике) / Галин Н.М., Кириллов Л.П. // М.: Энергоатомиздат, 1987. – 376 с.
12. Бухмиров В.В. Нестационарная теплопроводность. Справочные материалы для решения задач: метод. указ. / В.В. Бухмиров, С.В. Носова, Д.В Ракутина // Ивановский государственный энергетический университет им. Ленина, Иваново, 2005 – 32 с.
13. McBride B. J. NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species / Bonnie J. McBride, Dr. Michael J. Zehe, and Sanford Gordon // Report Number: NASA/TP-2002-211556, September 2002.
14. Зинченко А.В. Новый справочник химика и технолога, химическое равновесие. Свойства растворов. / А.В. Зинченко, С.Г.Изотова, А.В. Румянцев и др. С.-Пб.: АНО НПО "Профессионал", 2004, -998 стр.
15. Зайт В. Диффузия в металлах / В. Зайт. Перевод с немецкого. М.: Издательство иностранной литературы, 1958, - 381 с.
16. Жуков М.Ф. Электродуговые генераторы термической плазмы / М.Ф. Жуков, И.М. Засыпкин, А.Н. Тимошевский и др. Новосибирск: Наука, 1999. – 712 стр.
17. Halmann M. Carbothermal Reduction of Alumina: Thermochemical Equilibrium Calculations and Experimental Investigation / M. Halmann, A. Frei, and A. Steinfeld // Energy, 32(12), 2007, pp. 2420-2427.
18. Lacamera A.F. Carbothermic Aluminium Production using Scrap Aluminium as a Coolant / A.F. Lacamera // US Patent 6,475,260, 2002.
19. Кружилин Г. Н. Исследование теплового пограничного слоя / Г. Н. Кружилин // Журнал технической физики, 1936, т. 6, вып. 3, стр. 205.
20. Черный Г.Г. Газовая динамика / Г.Г. Черный. М.: Наука, Главная редакция физ. - мат. литературы, 1988, 424 с.

Список литературы на английском языке / References in English

1. Rybkina E. A. Rynok sintezirovannyh monokristallov (sapfirov): realii i perspektivy [The market of synthesized single crystals (sapphires): realities and prospects] / E. A. Rybkina // Innovacii [Innovations] No. 9 (215), 2016, pp. 106-110. [in Russian]
2. Popova A. N. Novye plazmennye tehnologii v materialovedenii i metallurgii [New plasma technologies in materials science and metallurgy] / A. N. Popova, V. E. Kison, A. S. Mustafaev et al. // Nanofizika i nanomaterialy. Sbornik nauchnyh trudov seminara 2020 [Nanophysics and Nanomaterials. Collection of scientific papers of the seminar 2020], St. Petersburg, pp. 282-285. [in Russian]
3. Boulos M.I. Fundamentals of plasma particle momentum and heat transfer / M.I. Boulos, P. Fauchais, A. Fardelle et al. // Plasma Spraying: Theory and Applications 1993, pp. 3-57.
4. Mikheev M. A. Osnovy teploperedachi [Fundamentals of heat transfer] / M. A. Mikheev. - M.-L.: GEI, 1956. - 390 p.
5. Zhukov M. F. Jelektrodugovye generatory termicheskoj plazmy [electric Arc generators of thermal plasma] / M. F. Zhukov, I. M. Zasypkin, A. N. Timoshevsky, etc. - Novosibirsk: Nauka. Sib. predpr. Academy of Sciences, 1999 – 712 p. [in Russian]
6. Angelist V. S. Teorija stolba jelektricheskoj dugi [Theory of post electric arc] / Angellist V. S., V. T. Gurovich, A. G. Tens, etc. - Novosibirsk: Nauka, 1990. – 375 p. [in Russian]
7. Landau, L. D. Gidrodinamika. Teoreticheskaja fizika [Hydrodynamics. Theoretical Physics]: vol. VI / L. D. Landau, E. M. Lifshits. 3rd ed., - M.: Nauka. Gl. ed. fiz-mat. lit., 1986, - 736 p. [in Russian]
8. Bukhmirov V. V. Raschet kojefficienta konvektivnoj teplootdachi (osnovnye kriterial'nye uravnenija) [Calculation of the convective heat transfer coefficient (basic criteria equations)]: method. the decree. [Electronic resource] / Bukhmirov V. V., Ivanovo State Power Engineering University named after Lenin, Ivanovo, 2007. – 39 p. URL: https://clck.ru/VsGNy (accessed 15.04.2021) [in Russian]
9. Aihara T. Effects of temperature-dependent fluid properties on heat transfer due to an axisymmetric gas jet impinging normal to a flat surface / T. Aihara, J. K. Kim, and S. Maruyama // Waerme - und Stofffibertragung 25 (1990), Sendai, Japan, pp. 145-153 (1990) DOI: 10.1007/BF01590145
10. Korsunov K. A Raschet parametrov jelektrodugovoj plazmy v kanale plazmotrona [Calculation of parameters of electric arc plasma channel is presented] / K. A. Korshunkov // Uspehi prikladnoj fiziki [advances in applied physics] 2013 №6. Vol. 1., pp. 724-733 [in Russian]
11. Galin N. M. Teplomassoobmen (v jadernoj jenergetike) [Heat and mass transfer (nuclear energy)] / N. M. Galin, L. P. Kirillov, // M.: Energoatomizdat, 1987. – 376 p. [in Russian]
12. Bukhmirov V. V. Nestacionarnaja teploprovodnost'. Spravochnye materialy dlja reshenija zadach [Non-stationary thermal conductivity. Reference materials for solving problems]: method. decree. / V. V. Bukhmirov, S. V. Nosova, D. V. Rakutina // Ivanovo State Power Engineering University named after Lenin, Ivanovo, 2005-32 p. [in Russian]
13. McBride B. J. NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species / Bonnie J. McBride, Dr. Michael J. Zehe, and Sanford Gordon // Report Number: NASA/TP-2002-211556, September 2002.
14. Zinchenko A.V. Novyj spravochnik himika i tehnologa, himicheskoe ravnovesie. Svojstva rastvorov [New Handbook of Chemist and Technologist, chemical equilibrium. Properties of solutions]. / A.V. Zinchenko, S. G. Izotova, A.V. Rumyantsev, et al. S.-Pb.: ANO NPO "Professional", 2004, -998 p. [in Russian]
15. Zayt V. Diffuzija v metallah [Diffusion in metals] / V. Zayt. Translated from German. Moscow: Publishing House of Foreign Literature, 1958, - 381 p. [in Russian]
16. Zhukov M. F. Jelektrodugovye generatory termicheskoj plazmy [Electric arc generators of thermal plasma] / M. F. Zhukov, I. M. Zasypkin, A. N. Timoshevsky, etc. Novosibirsk: Nauka, 1999 – 712 p. [in Russian]
17. Halmann M. Carbothermal Reduction of Alumina: Thermochemical Equilibrium Calculations and Experimental Investigation / M. Halmann, A. Frei, and A. Steinfeld // Energy, 32(12), 2007, pp. 2420-2427.
18. Lacamera A.F. Carbothermic Aluminium Production using Scrap Aluminium as a Coolant / A.F. Lacamera // US Patent 6,475,260, 2002.
19. Kruzhilin G. N. Issledovanie teplovogo pogranichnogo sloja [Investigation of the thermal boundary layer] / G. N. Kruzhilin // Zhurnal tehnicheskoj fiziki [Journal of Technical Physics], 1936, vol. 6, issue 3, p. 205. [in Russian]
20. Cherny G. G. Gazovaja dinamika [Gas dynamics] / G. G. Cherny. M.: Nauka, Main Editorial Office of phys. - checkmate. literature, 1988, 424 p. [in Russian]