РАЗРАБОТКА ПРИНЦИПИАЛЬНОЙ СХЕМЫ ДИОДНОГО СИНХРОННОГО АМПЛИТУДНОГО ДЕТЕКТОРА С ПРИМЕНЕНИЕМ МЕТОДОВ МАТЕМАТИЧЕСКОГО И СХЕМОТЕХНИЧЕСКОГО МОДЕЛИРОВАНИЯ

РАЗРАБОТКА ПРИНЦИПИАЛЬНОЙ СХЕМЫ ДИОДНОГО СИНХРОННОГО АМПЛИТУДНОГО ДЕТЕКТОРА С ПРИМЕНЕНИЕМ МЕТОДОВ МАТЕМАТИЧЕСКОГО И СХЕМОТЕХНИЧЕСКОГО МОДЕЛИРОВАНИЯ

Научная статья

Буренко Е.А.*

ORCID: 0000-0003-0660-0843,

Московский авиационный институт (национальный исследовательский университет), Москва, Россия

* Корреспондирующий автор (super.evgeny-burenko2012[at]yandex.ru)

Аннотация

Разработаны принципиальные схемы диодного синхронного последовательного и параллельного детекторов для демодуляции амплитудно-модулированного радиосигнала. Проведено математическое моделирование разработанного устройства методом несущей с применением математического аппарата функциональных звеньев и дифференциальных уравнений. Представлены осциллограммы сигналов в контрольных точках схем детекторов, полученные как на математической модели, так и на разработанной принципиальной схеме в результате схемотехнического моделирования. Произведена оценка сходимости результатов математического и схемотехнического моделирования (сравнение осциллограмм сигналов, формируемых математической моделью и осциллограмм, полученных на разработанных принципиальных схемах детектора).

Ключевые слова: амплитудный детектор, принципиальная схема, амплитудно-модулированный радиосигнал, модуляция, демодуляция, детектирование, фильтрация, метод несущей, метод дифференциальных уравнений, математическое моделирование, схемотехническое моделирование.

DEVELOPING A SCHEMATIC DIAGRAM OF A DIODE SYNCHRONOUS AMPLITUDE DETECTOR USING MATHEMATICAL AND CIRCUIT MODELING METHODS

Research article

Burenko E. A.*

ORCID: 0000-0003-0660-0843,

Moscow Aviation Institute (National Research University), Moscow, Russia

* Corresponding author (super.evgeny-burenko2012[at]yandex.ru)

Abstract

The current article introduces schematic diagrams of diode synchronous serial and parallel detectors for demodulation of an amplitude-modulated radio signal. The author carries out mathematical modeling of the developed device by the carrier method using the mathematical apparatus of functional links and differential equations. The waveforms of the signals at the control points of the detector circuits are also presented,  they were obtained both on a mathematical model and on the developed circuit diagram as a result of circuit modeling. The article also contains an estimation of convergence of the results of mathematical and circuit modeling (comparison of waveforms of signals generated by a mathematical model and waveforms obtained on the developed circuit diagrams of the detector).

Keywords: amplitude detector, circuit diagram, amplitude-modulated radio signal, modulation, demodulation, detection, filtering, carrier method, method of differential equations, mathematical modeling, circuit modeling.

Введение

В настоящее время широкое развитие вычислительной и компьютерной техники позволяет производить математическое и схемотехническое моделирование различных устройств в режиме реального времени. Целью настоящей статьи является разработка принципиальной схемы диодного синхронного амплитудного детектора двух типов – последовательного и параллельного с визуальным отображением осциллограмм сигналов в контрольных точках схемы. Для разработки принципиальных схем устройства предварительно осуществляется математическое моделирование всего тракта детектора. В ходе математического моделирования осуществляется расчёт, а затем оптимизация параметров схемы и всех необходимых характеристик устройств, входящих в состав детектора. Далее по разработанной и отлаженной математической модели осуществляется синтез принципиальной схемы всего устройства с дальнейшей отладкой, проводимой в ходе схемотехнического моделирования. После отладки принципиальной схемы производится оценка сходимости результатов математического и схемотехнического моделирования (для разрабатываемого устройства – это оценка качества выделения сигнала информационного параметра из амплитудно-модулированного радиосигнала).

Одним из наиболее мощных и эффективных средств математического моделирования различных устройств и процессов является среда компьютерной алгебры MathCAD, в которой разработана математическая модель детектора. Для моделирования был использован метод несущей с применением математического аппарата дифференциальных уравнений и эквивалентного ему аппарата функциональных звеньев [1]. Для разработки и моделирования принципиальной схемы детектора использовалась среда схемотехнического моделирования Electronics Workbench [6].

Общие сведения о методе моделирования

Для моделирования радиоустройств методом несущей с помощью дифференциальных уравнений необходимо описать уравнением каждый блок, входящий в схему. Уравнение блока связывает входные и выходные фазовые переменные. Предварительно осуществляется расстановка фазовых переменных. Выходная переменная каждого блока должна быть описана соответствующим уравнением. Если блок описывается уравнением высокого порядка, то это уравнение нужно представить в виде системы уравнений первого порядка путём введения вспомогательных переменных. В этом случае количество переменных, описывающих блок, будет равно порядку исходного уравнения. Из них одна будет выходной фазовой переменной блока.

Если уравнение не имеет производных от входной величины x(t), то преобразование может быть осуществлено следующим образом. Например, пусть имеется линейное однородное дифференциальное уравнение n-го порядка:

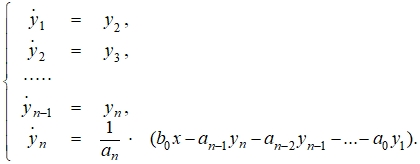    (1) или      (2) Вводя вспомогательные переменные y₁ ÷ y_n, оно преобразуется к виду:     (3)

Таким образом, получена система из n уравнений с n неизвестными. При этом выходной переменной, соответствующей y(t) в исходном уравнении будет переменная y₁. Нумерация переменных в схеме проводится с учётом всех вспомогательных переменных.

Если линейное динамическое звено задано передаточной функцией, её необходимо преобразовать в операторное уравнение, в которое входят изображения по Лапласу входной и выходной фазовых переменных X(p), Y(p), а также комплексная переменная p. Затем осуществляется переход к временнóй области путём взятия обратного преобразования Лапласа. При этом умножение функции на комплексную переменную p эквивалентно взятию производной от данной временнóй функции.

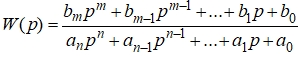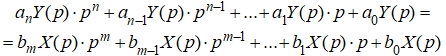Пусть имеется передаточная функция:    (4) Представив , получим операторное уравнение:     (5) Теперь взяв обратное преобразование Лапласа, получим линейное однородное дифференциальное уравнение n-го порядка: 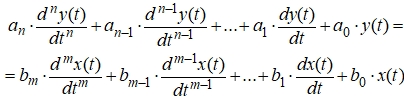     (6) или     (7)

Далее это уравнение раскладывается на систему уравнений первого порядка, которые представляются в правильной форме Коши. Решение уравнений осуществляется методом Рунге–Кутты четвёртого порядка с фиксированным шагом интегрирования [1].

Математическая модель амплитудного детектора

Амплитудным детектором называется радиоустройство, осуществляющее выделение сигнала информационного параметра из амплитудно-модулированного радиосигнала. При этом входной сигнал детектора моделируется методом решения дифференциального уравнения вида , где a₁, a₀ – коэффициенты, определяемые различными видами модуляции узкополосного сигнала, в частности, для амплитудно-модулированного радиосигнала, они равны [1]:

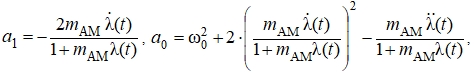
где m_AM – индекс амплитудной модуляции,

ω₀ = 2πf₀ – угловая частота несущего колебания [рад/с],

λ(t) – сигнал информационного параметра (модулирующий сигнал).

Сигнал информационного параметра λ(t) задаётся в виде гармонического процесса с угловой частотой Ω = 2πF с помощью дифференциального уравнения .

Полная структурная схема моделируемого амплитудного детектора представлена на рис. 1.

 

Рис. 1 – Полная структурная схема моделируемого амплитудного детектора

Здесь:

G_λ – генератор информационного параметра,

G_АМ – генератор амплитудно-модулированного сигнала,

АД – амплитудный детектор,

ФНЧ – фильтр нижних частот,

ФВЧ – фильтр верхних частот,

Ус – усилитель.

Моделируется диодный последовательный амплитудный детектор (рис. 2) и диодный параллельный амплитудный детектор (рис. 3).

Последовательный диодный амплитудный детектор (рис. 2) описывается дифференциальным уравнением:

    (8)

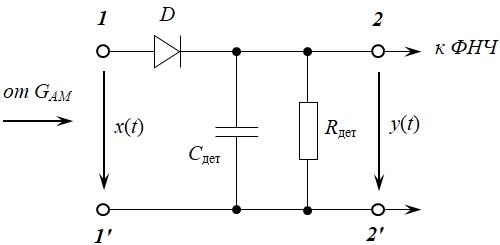
Рис. 2 – Последовательный диодный амплитудный детектор

  Параллельный диодный амплитудный детектор (рис. 3) описывается дифференциальным уравнением: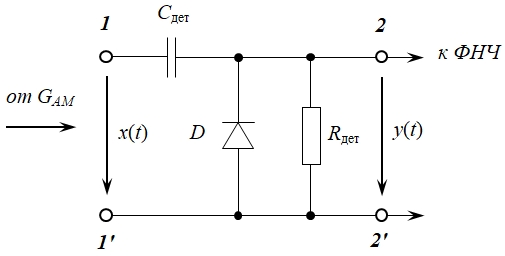    (9)  

Рис. 3 – Параллельный диодный амплитудный детектор

В уравнениях (8) и (9) i_д = G(u_д) – нелинейная вольт-амперная характеристика (ВАХ) диода, определяемая, в соответствии с моделью Эберса–Молла, следующим выражением [1]:

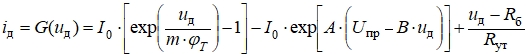     (10)

где:

I₀ = 10^–4 А – тепловой ток диода,

u_д – напряжение, приложенное к диоду; для схемы (рис. 2) оно равно u_д = x – y, для схемы (рис. 3) u_д = – y,

 ≈ 25,271 мВ – температурный потенциал, где k = 1,38 · 10^–23 Дж/К – постоянная Больцмана, q_e = 1,6 · 10^–19 Кл – заряд электрона, T = 293 К – температура окружающей среды при нормальных условиях (соответствует 20 °С),

m – эмпирический коэффициент, вводимый в режиме больших токов,

A, B – параметры, определяемые по обратной ветви вольт-амперной характеристики в области пробоя,

U_пр – напряжение пробоя,

R_б = (1 ÷ 2) Ом – сопротивление базы диода (под базой понимаются элементы конструкции, находящиеся вне p-n-перехода),

R_ут = (10 ÷ 20) Ом – сопротивление утечки диода,

R_дет – сопротивление в цепи детектора, C_дет – ёмкость в цепи детектора, выбираемая из условия: ,

τ_дет = R_детC_дет – постоянная времени детектора; она должна быть соизмерима с периодом несущего колебания τ_дет ≈ k_дет∙ T_нес, где k_дет – эмпирический коэффициент, определяемый экспериментальным путём.

Фильтр нижних частот представляется в виде пассивного LC-четырёхполюсника (рис. 4) и моделируется динамическим звеном шестого порядка с полиномиальной передаточной функцией [2], [3]:

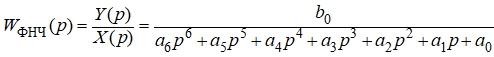     (11) при этом величина b₀ представляет собой коэффициент усиления фильтра на нулевой частоте.

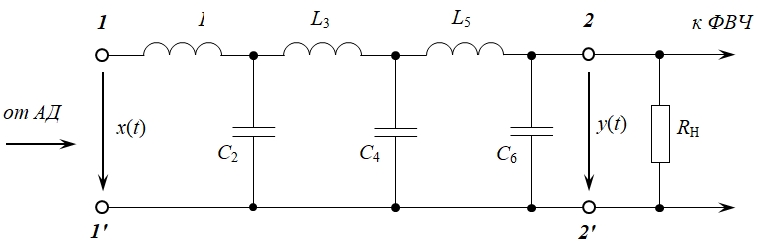
Рис. 4 – Пассивный LC-фильтр нижних частот шестого порядка

 

Применяя к данной передаточной функции обратное преобразование Лапласа, получается следующее дифференциальное уравнение:

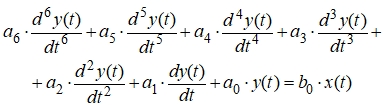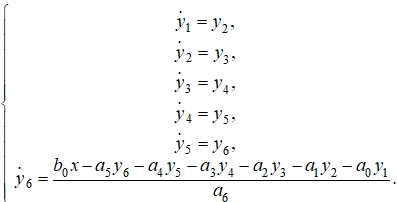    (12) или     (13) При переходе к правильной форме Коши получается система из шести дифференциальных уравнений первого порядка:     (14)

Коэффициенты a₀ ÷ a₆ зависят от вида фильтра и определяются методом аппроксимации амплитудно-частотной характеристики (АЧХ) фильтра. В модели используется оптимально монотонная аппроксимация АЧХ, как наиболее оптимальный вариант между аппроксимацией Баттерворта и Чебышёва I рода. Сам фильтр в данном случае будет являться оптимально монотонным [7].

Для низкочастотного оптимально монотонного фильтра шестого порядка с частотой среза ω_χ = 2πf_χ по уровню максимального затухания α_max = 2 дБ в полосе пропускания, коэффициенты a₀ ÷ a₆ дифференциального уравнения (13) определяются следующим образом:

Так как пассивные LC-фильтры не усиливают сигнал по мощности, то коэффициент усиления фильтра на нулевой частоте равен единице (b₀ = 1).

Частота среза f_χ ФНЧ выбирается из условия выделения фильтром сигнала информационного параметра и подавления сигнала несущего колебания (рис. 5).

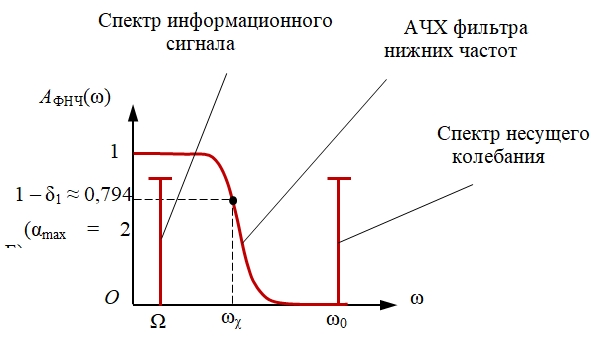Рис. 5 – Схема выбора частоты среза фильтра нижних частот

 

Нормированные значения элементов односторонне нагруженного оптимально монотонного LC-фильтра нижних частот шестого порядка (рис. 4) при нормированном сопротивлении нагрузки R_Н = 1 и максимальном затухании α_max = 2 дБ равны:

Значения элементов реального ФНЧ с заданными частотой среза ω_χ и сопротивлением нагрузки R_Н определяются по формулам денормирования [2]:

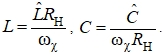
Фильтр верхних частот представляется динамическим звеном первого порядка в виде CR-цепи (рис. 6) с передаточной функцией [3], [4]:

     (15) где τ_ФВЧ = RC – постоянная времени ФВЧ.

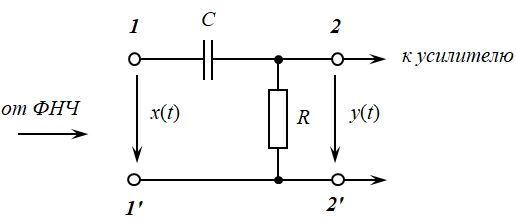
Рис. 6 – Пассивный CR-фильтр верхних частот первого порядка

 

Частота среза ФВЧ по уровню половинной мощности определяется соотношением:

При переходе к временнóй области получается дифференциальное уравнение:

    (16)

Постоянная времени ФВЧ выбирается из условия совпадения по фазе исходного информационного сигнала y₁ и сигнала y₁₃, получаемого на выходе всей схемы (рис. 1), и должна составлять τ_ФВЧ ≈ (0,01 ÷ 1) · T_мод, где T_мод – период модулирующего процесса.

Поскольку при моделировании схемы производная от входного сигнала x(t) ФВЧ вычисляется (при решении дифференциальных уравнений от впередистоящего звена, а именно ФНЧ), то в правильной форме Коши уравнение (16) будет иметь вид [1]:

    (17)

Усилитель повышает уровень сигнала, полученного на выходе ФВЧ, до заданного уровня 1 В. Поэтому он представляется простейшей схемой усиления входного сигнала без инверсии на операционном усилителе [3], [5] (рис. 7).

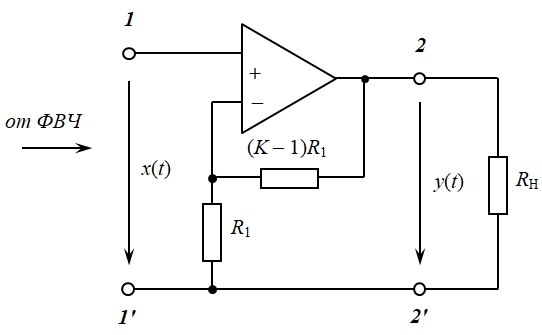
Рис. 7 – Неинвертирующий усилитель сигнала на операционном усилителе

 

Математическая модель данного устройства представляет собой безынерционное звено с постоянным коэффициентом усиления K, и может быть описана линейным алгебраическим уравнением:

y(t) = K · x(t).

Коэффициент усиления K выбирается из условия повышения уровня сигнала на выходе ФВЧ до заданного уровня 1 В.

Таким образом, полная структурная схема амплитудного детектора (рис. 1) описывается пятью дифференциальными уравнениями, первые два из которых второго порядка, а предпоследнее – шестого порядка, и одним линейным алгебраическим уравнением. Представив все уравнения в правильной форме Коши, получим систему из 13-ти уравнений. Вводя соответствующие переменные y₁ ÷ y₁₃, получим систему из 12-ти дифференциальных уравнений первого порядка и одного линейного алгебраического уравнения:

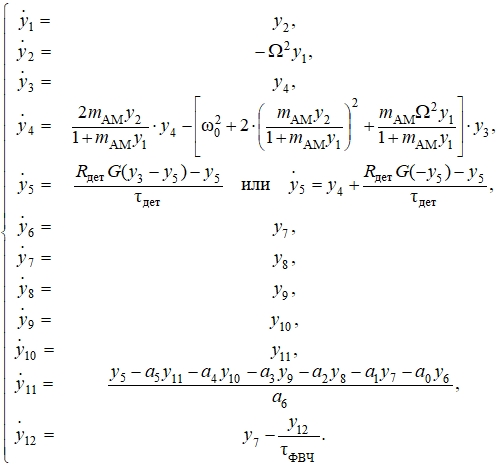     (18)

Численное решение данной системы уравнений, осуществляемое методом Рунге–Кутты четвёртого порядка с фиксированным шагом интегрирования, позволит определить выходные сигналы всех блоков структурной схемы (рис. 1). При решении численным методом для некоторых переменных задаются начальные условия:

Для контроля процессов, протекающих в схеме, в графическом режиме выводятся значения контрольных переменных y₁, y₃, y₅, y₆, y₁₂, y₁₃, которые указаны на структурной схеме (рис. 1).

Шаг моделирования (он же шаг интегрирования) должен быть как минимум на порядок-два меньше периода несущего колебания, а время моделирования выбирается из условия обзора трёх-пяти периодов модулирующего процесса.

Исходные данные для моделирования

Для моделирования были выбраны следующие исходные данные (параметры амплитудно-модулированного радиосигнала):

1. Частота информационного процесса: F = 1 кГц (период T_мод = 1 мс).
2. Частота несущего колебания: f₀ = 0,2 МГц = 200 кГц (период T_нес = 5 мкс).
3. Индекс амплитудной модуляции: m_AM = 0,8.

Результаты расчёта характеристик и параметров модели

В результате расчёта и дальнейшей оптимизации параметров и характеристик блоков модели были получены следующие результаты.

Найдены параметры вольт-амперной характеристики (ВАХ) полупроводникового диода (10), при которых обеспечивается наилучшее качество детектирования сигнала: m = 1, A = 12, B = 1, U_пр = –6 В, R_б = 1 Ом, R_ут = 20 Ом. Соответствующий график ВАХ диода представлен на рис. 8.

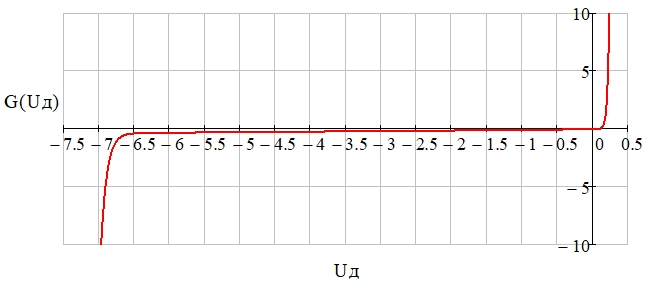
Рис. 8 – Вольт-амперная характеристика диода в соответствии с моделью Эберса–Молла

 

Найдены параметры цепи детектора (рис. 2 и 3): τ_дет = 2 мс, C_дет = 10 мкФ, R_дет = 200 Ом.

Найдены параметры фильтра нижних частот (рис. 4) и рассчитаны значения его элементов, при которых обеспечивается наилучшее качество детектирования сигнала: f_χ = 10 кГц, R_Н = 100 Ом, L₁ = 2,4942 мГн, C₂ = 283,7669 нФ, L₃ = 2,8258 мГн, C₄ = 258,0936 нФ, L₅ = 2,026 мГн, C₆ = 84,0402 нФ. График амплитудно-частотной характеристики рассчитанного ФНЧ представлен на рис. 9.

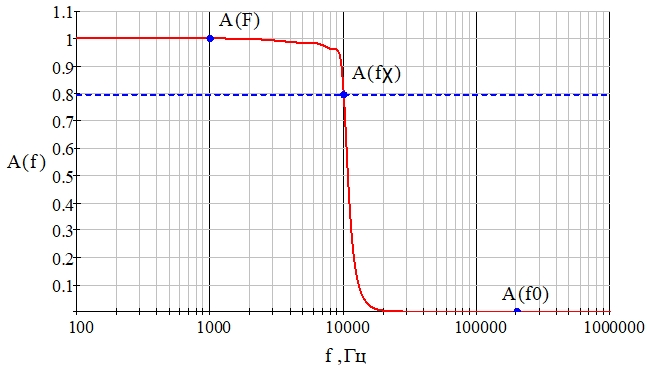
Рис. 9 – Амплитудно-частотная характеристика фильтра нижних частот

 

Найдены параметры фильтра верхних частот (рис. 6) и рассчитаны значения его элементов, при которых обеспечивается наилучшее качество детектирования сигнала: τ_ФВЧ ≈ 0,3 ∙ T_мод ≈ 0,3 мс, f_χʹ ≈ 530,516 Гц, R = 200 Ом, C ≈ 1,5 мкФ. График амплитудно-частотной характеристики рассчитанного ФВЧ представлен на рис. 10.

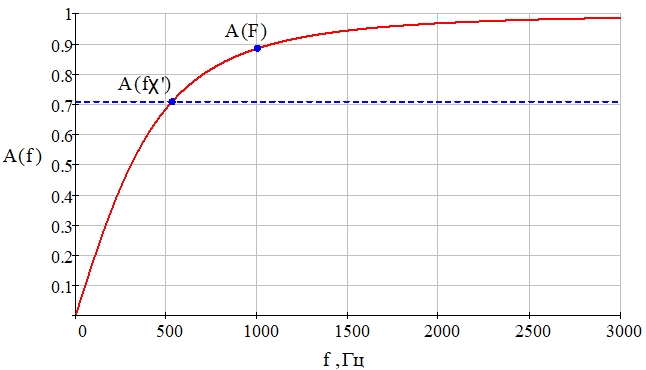
Рис. 10 – Амплитудно-частотная характеристика фильтра верхних частот

Найдены оптимальные параметры усилителя (рис. 7): K = 1,471, R₁ = 1 кОм, (K – 1)R₁ = 470,588 Ом.

Результаты математического моделирования

В результате математического моделирования получены осциллограммы сигналов в контрольных точках структурной схемы детектора (рис. 1).

Осциллограммы сигналов для схемы (рис. 1) с включённым последовательным диодным детектором (рис. 2) представлены на рис. 11 – 16.

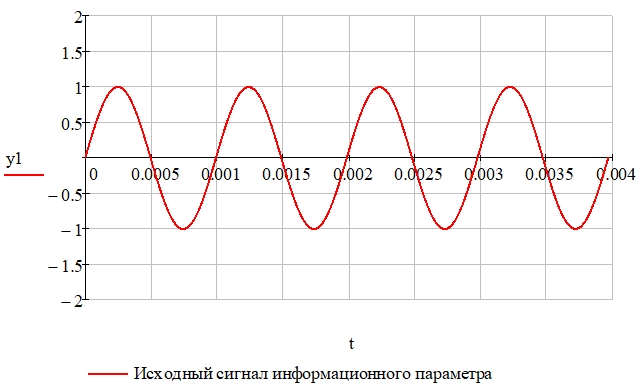
Рис. 11 – Исходный сигнал информационного процесса (переменная y₁)

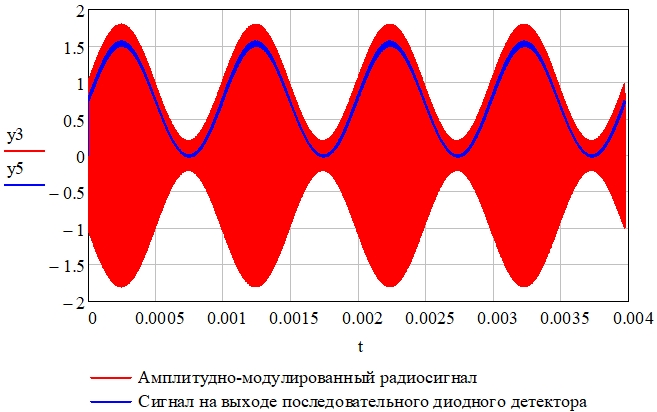
Рис. 12 – Амплитудно-модулированный радиосигнал (переменная y₃) и сигнал на выходе последовательного диодного детектора (переменная y₅)

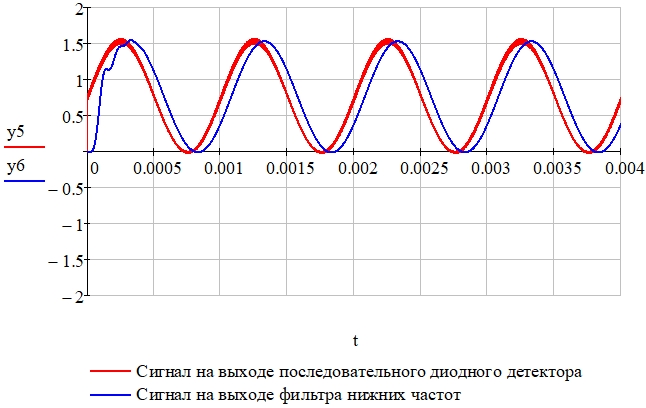
Рис. 13 – Сигналы на выходе последовательного диодного детектора (переменная y₅) и фильтра нижних частот (переменная y₆)

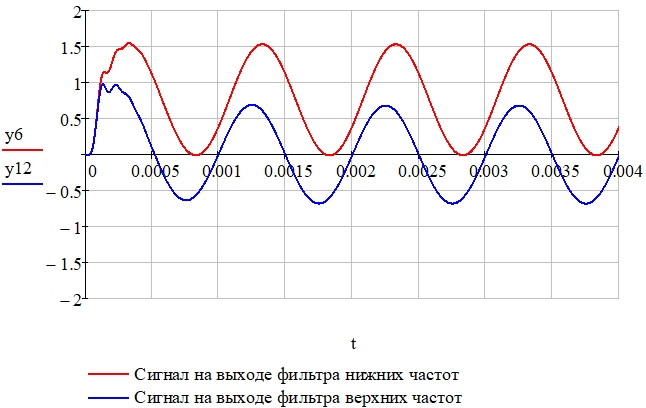
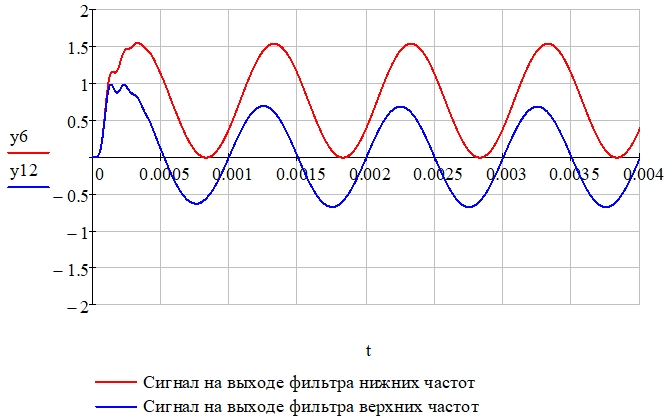
Рис. 14 – Сигналы на выходе и фильтров нижних (переменная y₆) и верхних (переменная y₁₂) частот

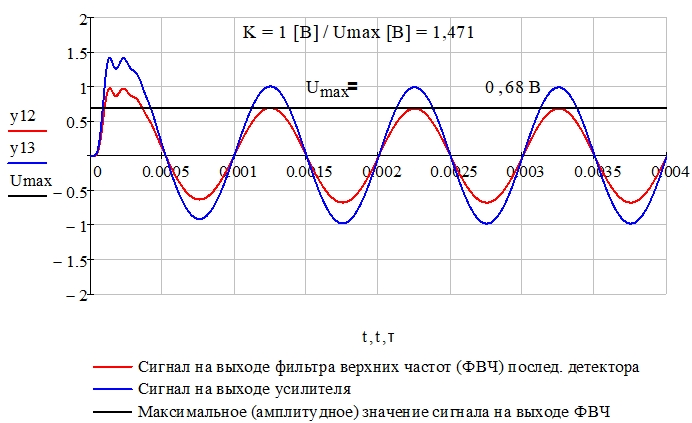
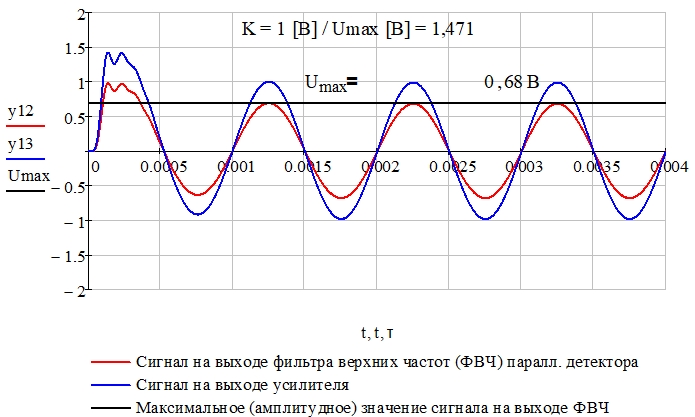
Рис. 15 – Сигналы на выходе фильтра верхних частот y₁₂ (указано амплитудное значение в установившемся режиме U_max = 0,68 В) и на выходе усилителя y₁₃

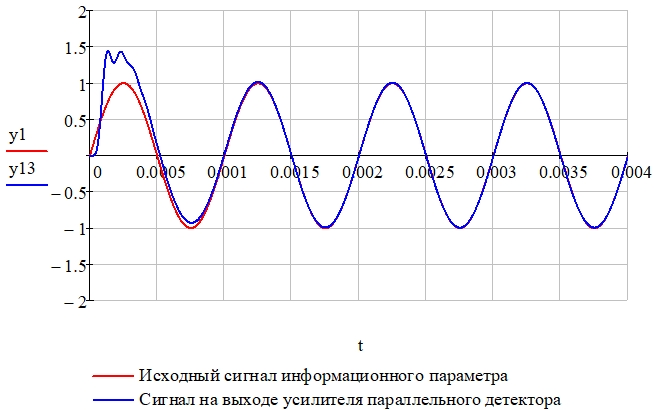
Рис. 16 – Сравнение исходного информационного процесса (y₁) и сигнала на выходе усилителя y₁₃ (коэффициент усиления K = 1 [В] / U_max [В] = 1,471)

 

Осциллограммы сигналов для схемы (рис. 1) с включённым параллельным диодным детектором (рис. 3) представлены на рис. 17 – 21.

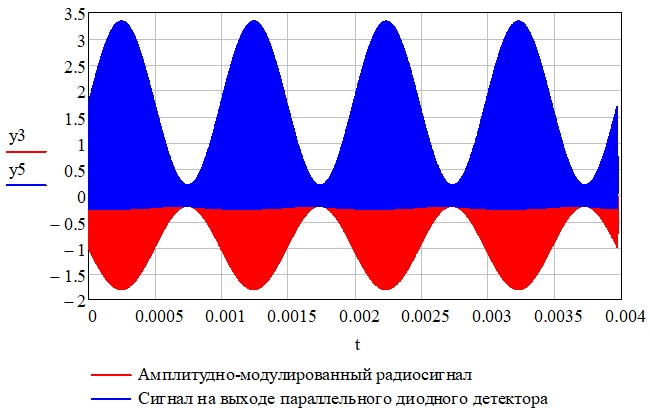
Рис. 17 – Амплитудно-модулированный радиосигнал (y₃) и сигнал на выходе параллельного диодного детектора (y₅)

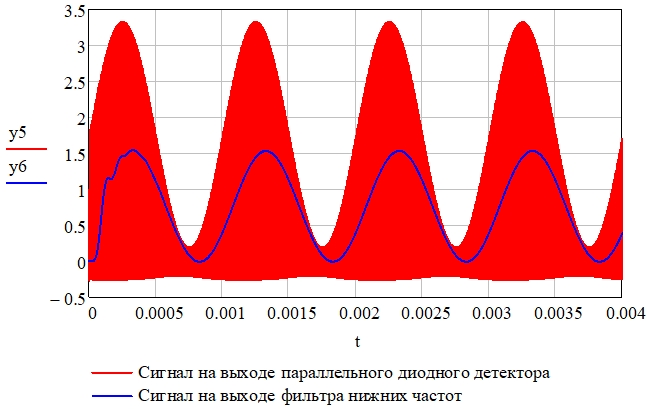
Рис. 18 – Сигналы на выходе параллельного диодного детектора (y₅) и фильтра нижних частот (y₆)

Рис. 19 – Сигналы на выходе и фильтров нижних (y₆) и верхних частот (y₁₂)

Рис. 20 – Сигналы на выходе фильтра верхних частот y₁₂ (указано амплитудное значение в установившемся режиме U_max = 0,68 В) и на выходе усилителя y₁₃

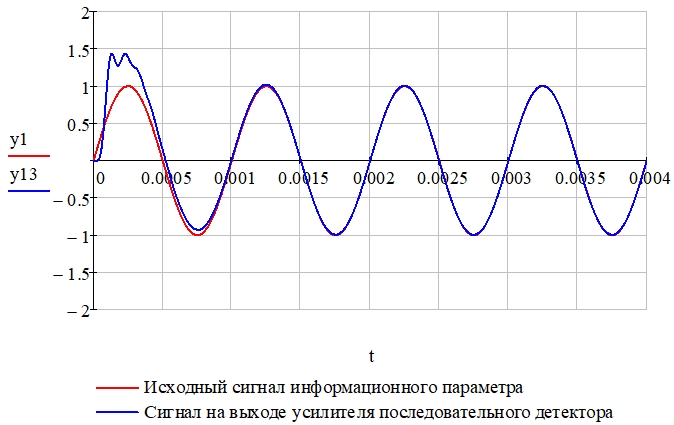
Рис. 21 – Сравнение исходного информационного процесса (y₁) и сигнала на выходе усилителя y₁₃ (коэффициент усиления K = 1 [В] / U_max [В] = 1,471)

Разработка принципиальной схемы амплитудного детектора

Таким образом, из результатов моделирования следует, что при найденных параметрах и характеристиках всех блоков структурной схемы детектора (рис. 1) обеспечивается наилучшее качество выделения информационного процесса из амплитудно-модулированного радиосигнала.

После проведения математического моделирования производится разработка принципиальной схемы детектора (рис. 22 и 23).

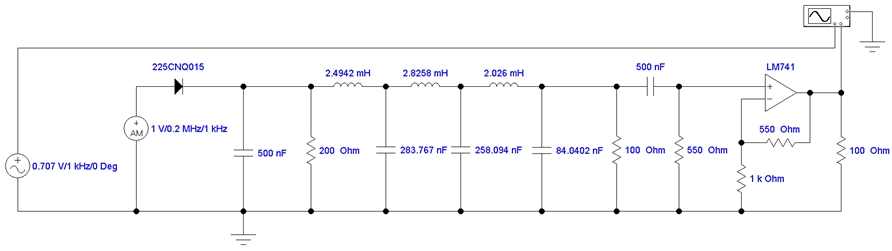
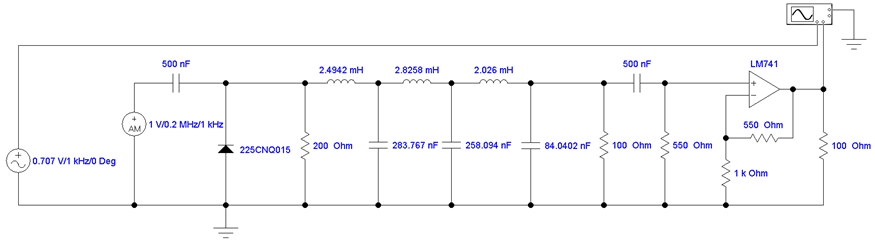
Рис. 25 – Принципиальная схема диодного последовательного амплитудного детектора с оптимизированными параметрами в среде Electronics Workbench

Рис. 26 – Принципиальная схема диодного параллельного амплитудного детектора с оптимизированными параметрами в среде Electronics Workbench

 

Результаты схемотехнического моделирования

В результате схемотехнического моделирования разработанных принципиальных схем (рис. 25 и 26) получены осциллограммы сигналов в контрольных точках диодного последовательного (рис. 27 – 32) и диодного параллельного (рис. 27 и 33 – 37) детекторов, подтверждающие результаты численного математического моделирования в среде MathCAD.

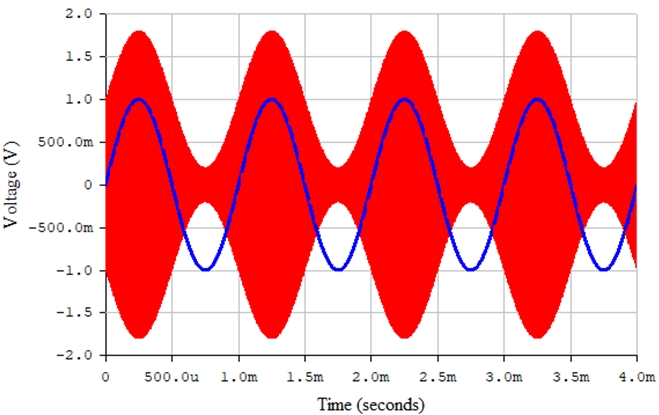
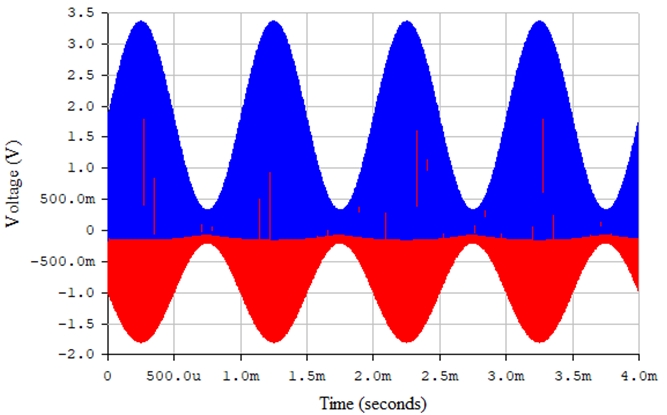
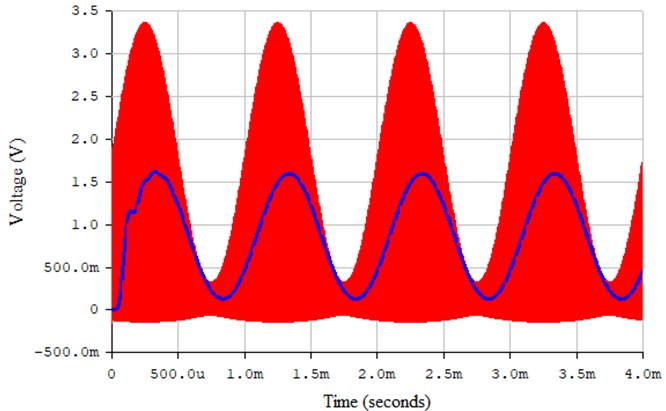
Рис. 27 – Амплитудно-модулированный радиосигнал (красная линия) и исходный информационный сигнал (синяя линия) в среде Electronics Workbench

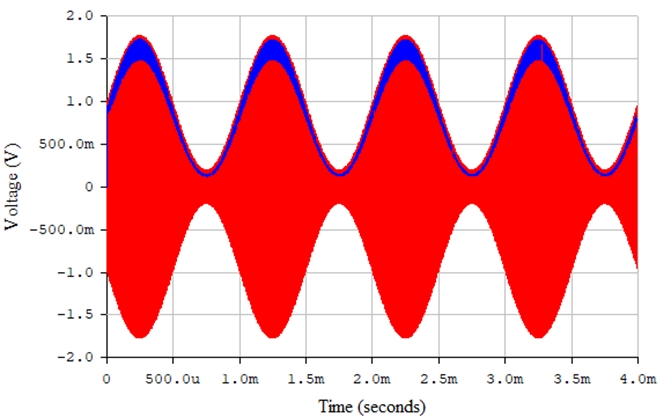
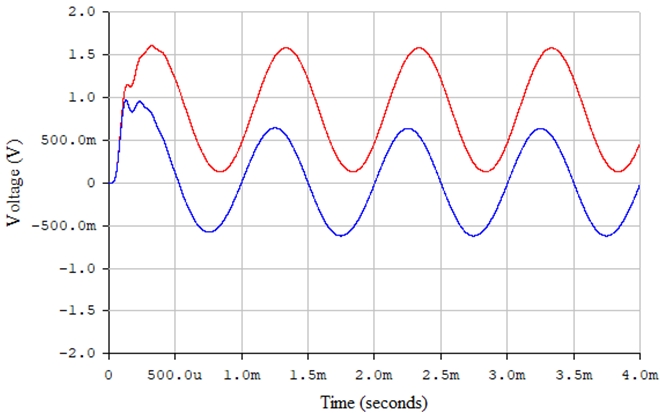
Рис. 28 – Амплитудно-модулированный радиосигнал (красная линия) и сигнал на выходе последовательного диодного детектора (синяя линия) в среде Electronics Workbench

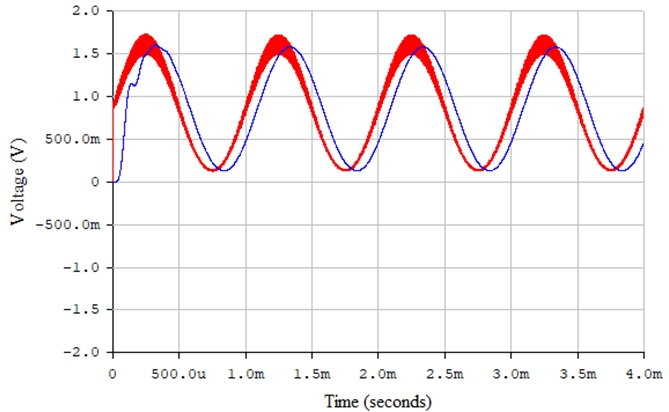
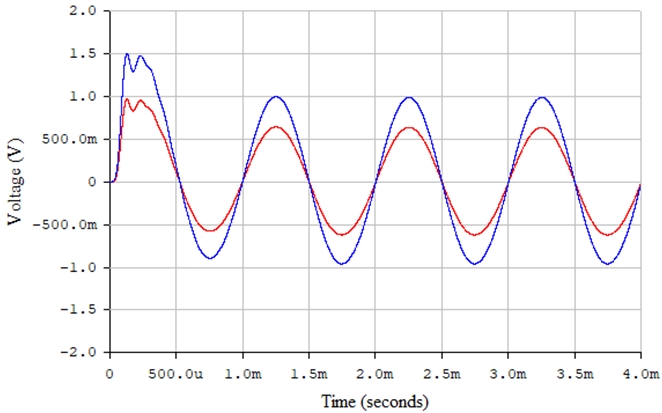
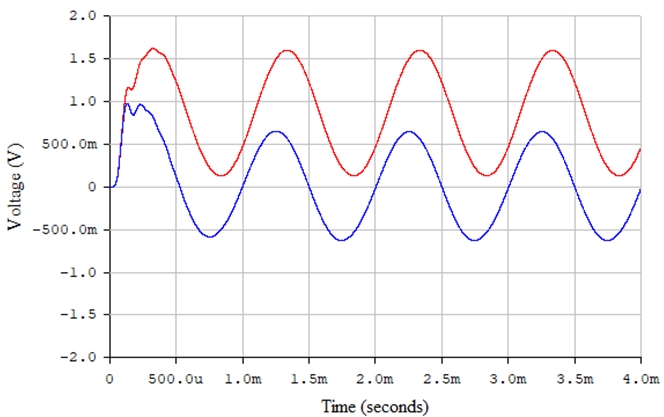
Рис. 29 – Сигналы на выходе последовательного диодного детектора (красная линия) и на выходе фильтра нижних частот (синяя линия) в среде Electronics Workbench

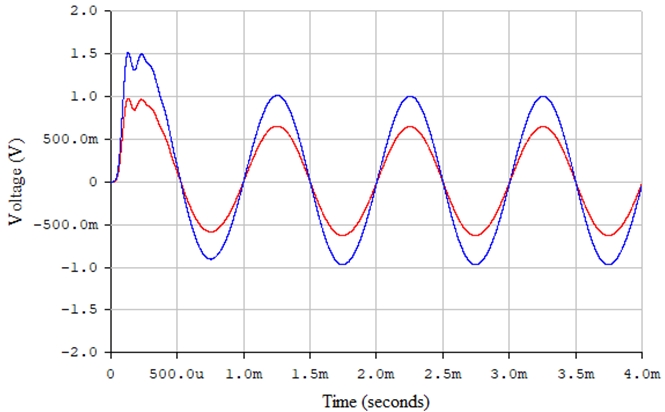
Рис. 30 – Сигналы на выходе фильтров нижних частот (красная линия) и верхних частот (синяя линия) в среде Electronics Workbench

Рис. 31 – Сигналы на выходе фильтра верхних частот (красная линия) и усилителя (синяя линия) в среде Electronics Workbench

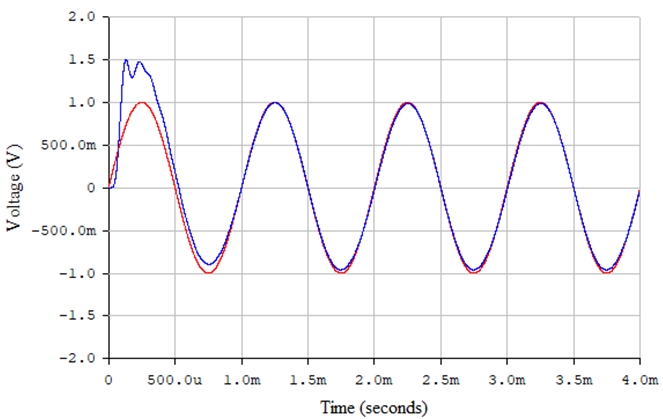
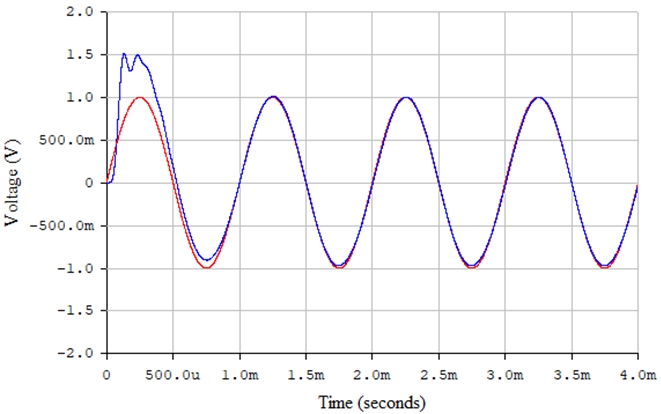
Рис. 32 – Сравнение исходного информационного процесса (красная линия) и сигнала на выходе усилителя (синяя линия) в среде Electronics Workbench (последовательный детектор, оптимизированный коэффициент усиления K = 1 [В] / U_max [В] = 1,55)

Рис. 33 – Амплитудно-модулированный радиосигнал (красная линия) и сигнал на выходе параллельного диодного детектора (синяя линия) в среде Electronics Workbench

Рис. 34 – Сигналы на выходе параллельного диодного детектора (красная линия) и на выходе фильтра нижних частот (синяя линия) в среде Electronics Workbench

Рис. 35 – Сигналы на выходе фильтров нижних частот (красная линия) и верхних частот (синяя линия) в среде Electronics Workbench

Рис. 36 – Сигналы на выходе фильтра верхних частот (красная линия) и усилителя (синяя линия) в среде Electronics Workbench

Рис. 37 – Сравнение исходного информационного процесса (красная линия) и сигнала на выходе усилителя (синяя линия) в среде Electronics Workbench (параллельный детектор, оптимизированный коэффициент усиления K = 1 [В] / U_max [В] = 1,55)

 

Анализ полученных результатов математического (рис. 11 – 21) и схемотехнического (рис. 27 – 37) моделирования показывает, что смоделированные процессы соответствуют реальным процессам в амплитудном детекторе. Применение метода дифференциальных уравнений позволяет выполнять проектирование различных электронных устройств на уровне функциональных и принципиальных схем.

Заключение

Таким образом, в работе описан способ разработки и оптимизации принципиальных схем радиотехнических и электронных устройств различного назначения (на примере амплитудного детектора) с применением методов численного математического моделирования на основе решения дифференциальных уравнений. Применение численного математического моделирования позволяет значительно повысить точность теоретического расчёта и практической оптимизации параметров принципиальных схем при разработке данных электронных устройств.

Конфликт интересов	Conflict of Interest
Не указан.	None declared.

Список литературы / References

1. Быков А.В. Основы математического моделирования радиоэлектронных устройств: Учебное пособие по курсу «Основы компьютерного проектирования и моделирования радиоэлектронных средств» / А.В. Быков, В.В. Харитонов; Федер. гос. бюдж. образоват. учреждение высш. проф. образования «Моск. авиац. ин-т (Нац. исслед. ун-т) (МАИ)». Фил. «Взлёт», г. Ахтубинск. – Волгоград: Изд-во ВолГУ, 2012. – 232 с.
2. Нестеров С.В. Синтез линейных электрических цепей / С.В. Нестеров. – Волгоград: Изд-во ВолГУ, 2013. – 84 с.
3. Улахович Д.А. Основы теории линейных электрических цепей / Д.А. Улахович. СПб.: БХВ-Петербург, 2009. – 816 с.
4. Баскаков С.И. Радиотехнические цепи и сигналы / С.И. Баскаков. – М.: Высшая школа, 2016. – 528 с.
5. Волович Г.И. Схемотехника аналоговых и аналого-цифровых электронных устройств / Г.И. Волович. – М.: Издательский дом «Додэка-XXI», 2005. – 528 с.
6. Карлащук В.И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и её применение / В.И. Карлащук. – М.: Салон-Р, 2000. – 506 с.
7. Буренко Е. А. Аппроксимация амплитудно-частотных характеристик и синтез по ним радиотехнических фильтров высокого порядка на основе полиномов Лежандра, Гегенбауэра и Якоби / Е. А. Буренко // Международный научно-исследовательский журнал. – 2021. – Выпуск № 6 (108) от 17.06.2021 г., Часть 1. – С. 49 – 63. DOI: 10.23670/IRJ.2021.108.6.009

Список литературы на английском языке / References in English

1. Bykov A.V. Osnovy matematicheskogo modelirovanija radiojelektronnyh ustrojstv: Uchebnoe posobie po kursu «Osnovy komp'juternogo proektirovanija i modelirovanija radiojelektronnyh sredstv» [Fundamentals of mathematical modeling of radio-electronic devices: A textbook for the course "Fundamentals of computer design and modeling of radio-electronic means"] / A.V. Bykov, V.V. Haritonov // Feder. gos. bjudzh. obrazovat. uchrezhdenie vyssh. prof. obrazovanija «Mosk. aviac. in-t (Nac. issled. un-t) (MAI)». Fil. «Vzljot» [«Vzljot», branch of the Moscow Aviation Institute (National Research University)], Ahtubinsk. – Volgograd: VolGU publishing house, 2012. – p. 232 [in Russian]
2. Nesterov S.V. Sintez linejnyh jelektricheskih cepej [Synthesis of Linear Electric Circuits] / S. V. Nesterov. - Volgograd: Publishing house VolGU, 2013. – p. 84 [in Russian]
3. Ulahovich D.A. Osnovy teorii linejnyh jelektricheskih cepej [Fundamentals of the Theory of Linear Electric Circuits] / D. A. Ulanovich. SPb.: BHV-Peterburg, 2009. – p. 816 [in Russian]
4. Baskakov S.I. Radiotehnicheskie cepi i signaly [Radio Engineering Circuits and Signals] / S. I. Baskakov. – M.: Vysshaja shkola, 2016. – p. 528 [in Russian]
5. Volovich G.I. Shemotehnika analogovyh i analogo-cifrovyh jelektronnyh ustrojstv [Circuitry of Analog and Analog-Digital Electronic Devices] / G. I. Volovich. – M.: Dodjeka-XXI, 2005. – p. 528 [in Russian]
6. Karlashhuk V.I. Jelektronnaja laboratorija na IBM PC. Programma Electronics Workbench i ejo primenenie. [Electronic Laboratory on an IBM PC. The Electronics Workbench Program and Its Application.] / V. I. Karlashhuk – M.: Salon-R, 2000. – p. 506 [in Russian]
7. Burenko E. A. Approksimacija amplitudno-chastotnyh harakteristik i sintez po nim radiotehnicheskih fil'trov vysokogo porjadka na osnove polinomov Lezhandra, Gegenbaujera i Jakobi [Approximation of Amplitude-Frequency Characteristics and Synthesis of High-Order Radio Engineering Filters Based on Legendre, Gegenbauer and Jacobi Polynomials] / E. A. Burenko // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. – 2021. – Issue № 6 (108) ot 17.06.2021 g., Part 1. – pp. 49 – 63. DOI: 10.23670/IRJ.2021.108.6.009 [in Russian]