МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МЕЛАНОМЫ

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МЕЛАНОМЫ

Научная статья

Гончарова А.Б.^1, *, Зимина Е.И.², Колпак Е.П.³

^{1, 2, 3} Санкт-Петербургский государственный университет, Санкт-Петербург, Россия

* Корреспондирующий автор (a.goncharova[at]spbu.ru)

Аннотация

Разработана математическая модель четырехстадийной поверхностно растущей меланомы. Модель представлена задачей Коши для системы четырех обыкновенных дифференциальных уравнений. Стадии заболевания моделируются камерами различной емкости с перемещением злокачественных клеток из камеры в камеру. В модели химиотерапии учитывается прямое действие препаратов на опухолевые клетки на заданном временном интервале. С применением статистического подхода разработана модель построения распределения условных «больных» по времени постановки диагноза, продолжительности лечения и времени наступления рецидива. Дана оценка расхода количества препаратов на лечение до заданного требуемого уровня выживаемости. Параметры модели определяются исходя из клинических данных по скорости роста новообразования, временного промежутка лечения.

Ключевые слова: дифференциальные уравнения; математическое моделирование; модель лечения; новообразование; рецидив; устойчивость.

MATHEMATICAL MODEL OF MELANOMA

Research article

Goncharova A.B.^1, *, Zimina E.I.², Kolpak E.P.³

^{1, 2, 3} Saint Petersburg State University, Saint Petersburg, Russia

* Corresponding author (a.goncharova[at]spbu.ru)

Abstract

The current article introduces a mathematical model of a growing four-stage surface melanoma. The model is represented by the Cauchy problem for a system of four ordinary differential equations. The stages of the disease are modeled by chambers of various capacities with the movement of malignant cells from chamber to chamber. The chemotherapy model takes into account the direct effect of drugs on tumor cells at a given time interval. Using a statistical approach, the authors develop a model for constructing the distribution of patients by the time of diagnosis, the duration of treatment, and the time of relapse. Also, the article provides an estimation of the drugs to be consumed for treatment to a given required level of survival. The model parameters are determined based on clinical data on the growth rate of the neoplasm, the time interval of treatment.

Keywords: differential equations; mathematical modelling; treatment model; neoplasm; relapse; resistance.

Введение

Меланома в ряду злокачественных новообразований не является наиболее распространенным онкологическим заболеванием. Но по своей агрессивности не уступает таким локализациям как рак легких у мужчин и рак молочной железы у женщин. Рост числа больных меланомой в России растет последние 30 лет независимо от методов количественной оценки заболевших, вылеченных, умерших [1]. Когорта больных в стране, как в абсолютном выражении, так и в расчете на 100 000 населения увеличивается на 3,5% в год. В возрастных группах старше 50 лет темпы роста «грубого показателя» достигают 5,5%. По всем локализациям меланомы после постановки на учет около 30% умирает в течение 5 лет. Смертность на первом году лечения достигает 15% от обратившихся за помощью лиц. Временной промежуток от среднего возраст постановки диагноза до среднего возраста смертности около 2-х лет [1].

Ожидаемые результаты лечения зачастую остаются неудовлетворительными из-за позднего обращения за медицинской помощью. Около 25% больных обращаются за помощью, имея IV стадию заболевания с множественными метастазами. Не всегда эффективна и химиотерапия, поскольку опухолевые клетки в процессе воздействия на них постепенно приобретают стойкость к препаратам. Достоверность действия лекарств зачастую имеет низкую статистическую достоверность [2].

Меланома является злокачественным заболеванием верхнего слоя кожи – эпидермиса. Постоянное обновление клеток эпидермиса происходит за счет кератиноцитов, образующихся в нижнем слое эпидермиса. Цикл обновления клеток эпидермиса длится 26-28 суток. Одновременно с кератиноцитами в нижнем слое эпидермиса образуются и меланоциты, придающие цвет коже.

Меланоциты могут скапливаться в эпидермисе в виде небольших пятен. В отдельных меланоцитах под действием внутренних и внешних факторов могут быть нарушены механизмы передачи сигналов, затрагивающих клеточный апоптоз [3]. Это и является основной причиной неограниченного роста меланомы. Временные промежутки возникновения меланом в пределах одного анатомического могут составлять несколько лет [4]. В результате может начаться процесс бесконечного деления меланоцитов и, соответственно, увеличение их количества с последующим распространением образовавшегося скопления вдоль поверхности эпидермиса. Таким образом, небольшое пятно меланоцитов может превратиться в злокачественную опухоль постоянно делящихся клеток, поверхностно распространяющуюся в виде плоского пятна [5], [6]. Поперечные размеры опухоли, в зависимости от органа, на котором она растет, могут быть более 10 см. Линейный рост опухоли может достигать 0,25 мм в день [7]. При этом индекс митотической активности может зависеть от поперечных размеров опухоли, и увеличиваться с ростом ее размеров. Удельная скорость роста популяции делящихся клеток по разным оценкам изменяется в диапазоне от 0.003 до 0.100 1/день [8], [9].

Современные методы лечения больных меланомой кожи предусматривают использование хирургических, лучевых, лекарственных методов или их комбинаций. Однако практические результаты лечения остаются неудовлетворительными: высока частота рецидивов, короткий срок дожития после лечения. На первое место выходит лекарственная профилактика после хирургического вмешательства [2]. В клинической практике химиотерапия включает в себя несколько препаратов, попеременно принимаемых больным. Курс лечения может продолжаться от нескольких дней до нескольких недель и повторяться несколько раз. Лечение может продолжаться несколько месяцев [10], [11].

Математическая модель

Математических модели злокачественных новообразований разрабатываются на основе аппарата обыкновенных дифференциальных уравнения или уравнений в частных производных [12]. Аналогичный подход предложен и в работах [13], [14], [15], в которых моделируется рост меланомы без разделения на стадии. Не рассматриваются и варианты лечения, позволяющие оценить увеличение продолжительности жизни пациентов.

В модели радиального роста популяции делящихся клеток пренебрегается толщиной эпидермиса, считается, что кератиноциты не мешают росту опухоли вдоль поверхности. Численность популяции делящихся клеток, как отмечается в экспериментальных работах, описывается экспоненциальной зависимостью [16], [17], [18]. Однако функциональное пространство, в котором размножаются делящиеся клетки ограничено плоскостью. Поскольку вертикальный рост радиально распространяющейся опухоли незначителен, а плотность клеточной массы в очаге возникновения не может быть бесконечно большой, то размножающиеся клетки после достижения предельного значения плотности начнут распространяться вдоль поверхности. С учетом этого считается, что численность популяции делящихся клеток описывается логистической зависимостью.

Заболевание в клинической практике условно подразделяется на четыре стадии, каждой из которой сопоставляется конкретный поперечный размер опухоли. В [16] линейный размер первой зоны принимается равной 2 см, второй – 3 см, третьей – 5 см, четвертой – 10 см. С учетом этого положения в модель вводятся четыре зоны разного размера, в которых размножаются делящиеся клетки. В начальный момент времени делящиеся клетки возникают в первой зоне, а по достижении некоторого количества часть делящихся клеток начинает перемещаться во вторую зону. После наполнения второй зоны начинается перемещение в последующие зоны. Введенные зоны можно сопоставлять со стадиями заболевания.

Химические препараты, необходимые для уничтожения делящихся клеток, свободно поступают через базальную мембрану в эпидермис. Поскольку делящиеся клетки распространяются параллельно дерме, то в модели считается, что в каждую зону поступает одинаковое количество препаратов, предназначенных для уничтожения делящихся клеток. Уничтожение делящихся клеток происходит при непосредственном контакте препаратов и делящихся клеток, а скорость уничтожения пропорциональна численности клеток и концентрации препаратов.

С учетом этих предположений и ограниченности функционального пространства каждой зоны модель распространения делящихся клеток примет вид

 

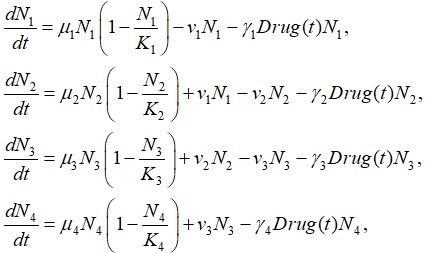
где  ‑ количество делящихся клеток в k-й зоне ,  ‑ удельные скорости роста популяций делящихся клеток в каждой из зон, а  ‑ емкости зон,  ‑ доля клеток, переходящих из одной зоны в другую  ‑ количество лекарственных препаратов, уничтожающих делящиеся клетки,  – параметры, характеризующие скорости уничтожения делящихся клеток препаратами. Под емкостью зон понимается максимальное количество делящихся клеток, которое может находиться в зоне. Заполнение четвертой зоны сопоставляется с началом роста опухоли в вертикальном направлении.

Программы лечения больных состоят из нескольких курсов применения чередующихся в течение нескольких дней препаратов [10], поступающих в функциональное пространство в заданном в протоколе лечения количестве. Поскольку лечение длится несколько месяцев, то можно принять, что на временном промежутке лечения подается одно и то же количество препаратов с усредненным действием:

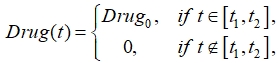   (2)

где t₁ ‑ момент времени начала лечения, а t₂ ‑ момент времени окончания лечения,  ‑ количество вводимых препаратов в единицу времени. Расход препаратов подсчитывается по формуле

К системе уравнений (1) добавляются начальные условия

соответствующие случаю возникновения небольшого количества  делящихся клеток в первой зоне.

Из первого уравнения в (1) при  следует, что в первой зоне равновесное состояние

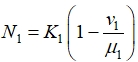
реализуется, если выполняется неравенство , и оно будет устойчивым. В противном случае устойчивым будет состояние . То есть это неравенство является необходимым условием роста численности популяции делящихся клеток.

Устойчивая стационарная точка второго уравнения в (1) при  находится как положительный корень квадратного уравнения

 

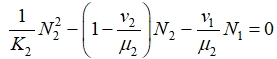
Аналогичным образом определяются стационарные значения . То есть при появлении в первой зоне делящихся клеток они постепенно будет распространяться и в остальные зоны при условии выполнения неравенства .

При наличии лекарственных препаратов делящиеся клетки в первой зоне будут убывать, если  выполняется неравенство . Аналогичными необходимыми условиями убыли делящихся клеток в остальных зонах являются

Результаты моделирования

Таким образом, модель (1) объясняет рост популяции делящихся клеток высокой скоростью их размножения по сравнению с линейной скоростью распространения. Лекарственная терапия может быть эффективной в том случае, если скорость уничтожения делящихся клеток препаратами будет больше, чем скорость размножения клеток. В рамках модели (1)-(2) можно оценить зависимость времени «лечения» опухоли от количества расходованных препаратов. За «базовые» значения параметров приняты

    (3)

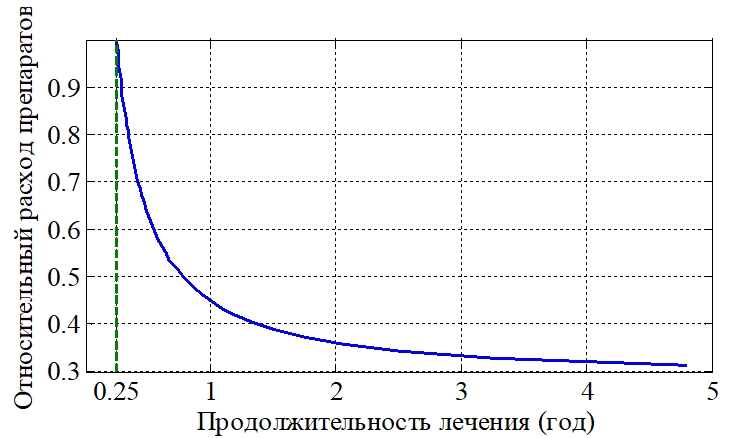
На рис. 1 отражена эта зависимость расхода препаратов от продолжительности лечения: лечение считалось законченным при достижении неравенств   За единичный расход принят расход, при котором делящиеся клетки уничтожаются за 1/4 года (момент времени на рис. 1 отмечен вертикальной пунктирной линией). Как следует из анализа полученных результатов (рис. 1) зависимость «расход препаратов - время лечения» не является линейной. Вместе с тем она отражает естественное понимание влияния препаратов: чем эффективнее препарат, тем короче процесс лечения. Зависимость на рис.1 является усредненной для 50 000 наборов параметров системы уравнений (1), выбранных случайным образом, но не отличающихся от значений (3) более чем в три раза.

Рис. 1 – График усредненной зависимости расхода препаратов от продолжительности «лечения» для 50 000 условных больных

  Математическая модель статистики лечения

Параметры  в системе уравнений (1)-(2) сопоставляются с конкретным «больным». Выбирая случайным образом эти параметры n раз, можно построить распределение больных по времени постановки диагноза, времени окончания лечения и времени наступления рецидива [19]. 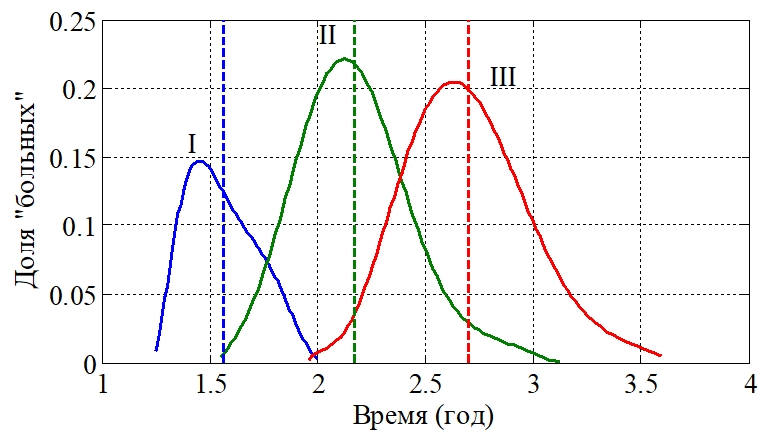За время постановки диагноза принимается время достижения заданного значения  (принято ) [20], за время окончания «лечения» ‑ время достижения диагностически неопределимого значения количества делящихся клеток (принято ), за время наступления рецидива – время достижения значения , установленного на момент постановки «диагноза» (принято ). На рис. 2 отражено распределение «больных» по времени постановки диагноза (крива I), по времени окончания лечения (кривая II) и времени наступления рецидива (кривая III) для 50 000 условных больных. Средние значения для зависимости I – 1.6 года, для зависимости II ‑ 2.2 года, для зависимости III – 2.7 года, отмечены вертикальными линиями. Параметры выбирались случайным образом, отличающимися от значений (3) не более чем в три раза. При заданных значениях параметров системы уравнений (1)  выбиралось таким образом

 

где  ‑ собственные значения матрицы Якоби правой части системы уравнений (1) в точке . При таком выборе параметра  тривиальная стационарная точка системы уравнений будет устойчивой.

Рис. 2 – Графики распределения больных по времени постановки «диагноза» (зависимость I), по времени окончания «лечения» (зависимость II), по времени наступления «рецидива» (зависимость III)

 

Полученные расчетные значения момента постановки диагноза, промежутка времени от окончания лечения до возникновения рецидива согласуются со статистическими данными: согласно данным различных авторов, 2-х летняя безрецидивная выживаемость после радикального лечения первичной опухоли составляет около 40 %, а общая выживаемость — около 50 – 60 %. Медиана выживаемости может достигать 3-х лет [21]. В клинической практике обращение за медицинской помощью может происходить от нескольких месяцев до нескольких лет после начала заболевания [22], [23]. Поздние сроки обращения происходят при IV стадии заболевания. Медиана выживаемости в этом случае может составлять 6-7 месяцев, а продолжительность жизни – 10-11 месяцев. В условно принятой IV стадии заболевания при выбранном наборе параметров среднее (3) время постановки «диагноза» ‑ 18 месяцев, продолжительность лечения – 7 месяцев, а продолжительность периода от окончания лечения до наступления условного «рецидива» – 6 месяцев, среднее время «жизни» от постановки диагноза до рецидива 13 месяцев. Эти показатели согласуются с данными клинических исследований. Разработанный вероятностный подход оценки времени достижения определенного размера опухоли может быть использован при адаптивной терапии [24] для определения оптимального времени для точек переключения лечения с учетом специфики пациента.

Заключение

Разработанный подход математического моделирования роста меланомы и прогнозирования статистических показателей заболеваемости и результатов лечения позволяет оценить длительность лечения, обеспечивающую максимальную выживаемость больных. В дополнение к этому позволяет осуществить рациональный подбор препаратов при заданных наперед продолжительности лечения и экономических затратах.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. The State of Cancer Care Provided to the Population of Russia in 2018. Moscow: FSBI P.A. Herzen Moscow Cancer Research Institute, Branch Office of FSBI NMRRC, Ministry of Health of Russia; 2018. p. 236. [Electronic resource]. URL: https://nnood.ru/wp-content/uploads/2019/04/Statichticheskijj-ezhegodnik-Gercena-2018.pdf. (accessed: 12.06.2021)
2. Zakurdyaeva I.G. The treatment of patients with late relapses of skin melanoma with isolated metastatic regional lymph nodes involvement / I.G. Zakurdyaeva, A.F. Tsyb, V.S. Parshin et al. // Voprosy Onkologii. - 2012. - V. 58 (3). - P. 402-405.
3. Ruksha T. G. High throughput analysis of single cancer cells as the basis for personalized therapy of oncological diseases / T. G. Ruksha, E. Yu. Sergeeva, A. V. Komina // Tsitologiia. - - V. 59 (10). - P. 654-661.
4. Буров Д.А. Клиника Первично-множественная меланома кожи. Клинический случай / Д.А. Буров, Я.А. Божченко, А.А. Тарарыкова // Cаркомы костей, мягких тканей и опухоли кожи. - 2016. - № 1. - С -76-80.
5. Kopnin B.P. Genome instability and oncogenesis /P. Kopnin // Molecular Biology. - 2007. - V. 41 (2). - P. 329-339.
6. Cle´ment Chatelain, Pasquale Ciarletta, Martine Ben Amar Morphological changes in early melanoma evelopment:Influence of nutrients, growth inhibitors and cell-adhesion mechanisms // Journal of Theoretical Biology. - 2011. - V. 290. - P. 46–59. DOI:10.1016/j.jtbi.2011.08.029.
7. Снарская Е.С. Беспигментная узловая меланома кожи голени / Е.С. Снарская, К.М. Аветисян, В.В. Андрюхина // Российский журнал кожных и венерических болезней. - 2014. - № 2. - С. 4-7.
8. Проценко А. Таргетная терапия при меланоме, гастроинтестинальных стромальных опухолях, дерматофибросаркоме протуберанс / А. Проценко // Практическая онкология. - 2010. - Т. 11. - №3. – С. 1262-170.
9. Tsur N. Response of patients with melanoma to immune checkpoint blockade –insights gleaned from analysis of a new mathematical mechanistic model / N. Tsur, Y. Kogan, M. Rehm et al. // Journal of Theoretical Biology. - 2020. - V. 485. № 110033. DOI: 10.1016/j.jtbi.2019.110033.
10. Chu E. Physicians cancer chemotherapy drug manual / E. Chu, V.T. DeVita // Jones and Bartlett publishers. Boston, USA. 2007.
11. Закурдяева И.Г. Метастатическая меланома кожи (обзор литературы) / И.Г. Закурдяева, А.Ф. Цыб // Сибирский онкологический журнал. - 2010. - №6 (42). - С. 56-62.
12. Byrne H.M. The role of cell-cell interactions in a two-phase model for avascular tumour growth / H.M. Byrne, J.W. Breward, C.E. Lewis // Journal of Mathematical Biology. - 2001. - V. 45 (2). - P. 125 – 131.
13. Haridas P. Quantifying rates of cell migration and cell proliferation in co-culture barrier assays reveals how skin and melanoma cells interact during melanoma spreading and invasion / Parvathi Haridas, Catherine J. Penington, Jacqui A. McGovern et al. // Journal of Theoretical Biology. - 2017. - V. 423. - P. 13–25.
14. Albano G. Estimating and determining the effect of a therapy on tumor dynamics by means of a modified Gompertz diffusion process / Giuseppina Albano, Virginia Giorno, Patricia Román-Román et al. // Journal of Theoretical Biology. - 2015. - V. 364. - P. 206–219.
15. Akhmetzhanov A.R. Modelling bistable tumour population dynamics to design effective treatment strategies / Andrei R. Akhmetzhanov, Jong Wook Kim, Ryan Sullivan et al. // Journal of Theoretical Biology. - 2019. - V. 474. - P. 88–102. DOI: 10.1016/j.jtbi.2019.05.005.
16. Проценко С.А. Меланома кожи: новое в лекарственном лечении / С.А. Проценко // Природа. - 2018. - № 6. - С. 26-28.
17. Palkina, N.V. Prooncogenic effects of inhibiting the microRNA miR-106A in skin melanoma cells in vitro /V. Palkina, A.V. Komina, M.B. Aksenenko, et al. // Tsitologiia. - 2016. - V. 58 (9). - P. 679-687.
18. Rommelfanger D.M. Dynamics of melanoma tumor therapy with vesicular stomatitis virus: explaining the variability in outcomes using mathematical modeling / D.M. Rommelfanger, C.P. Offord, J. Dev et al. // Gene Therapy. - 2012. - V. 19. - 543–549.
19. Гончарова А.Б. Математическое моделирование лечения онкологического заболевания / А.Б. Гончарова, Е.П. Колпак, М.М. Расулова и др. // Вестник Санкт-Петербургского университета. Прикладная математика. Информатика. Процессы управления. 2020. Т. 16. № 4. С. 437-446DOI:21638/11701/SPBU10.2020.408.
20. Гончарова А.Б. Постановка предварительного медицинского диагноза на основе теории нечетких множеств с использованием меры Сугено / А.Б. Гончарова // Вестник Санкт-Петербургского университета. Прикладная математика. Информатика. Процессы управления. 2019. Т. 15. № 4. С. 529-543.DOI:21638/11702/spbu10.2019.409.
21. Тарков С.А. Особенности течения меланом кожи головы и шеи / С.А. Тарков, А.Е. Михнин, К.В. Шелехова и др. // Вопросы онкологии. - 2013. – Т. 59. - № 1. - С. 114-117.
22. Мяснянкин М.Ю. Подногтевая меланома / М.Ю. Мяснянкин, Г.И. Гафтон, В.В. Анисимов и др. // Эффективная фармакотерапия. - 2016. - Т. 39. - С. 40-44.
23. Kolpak E.P. Oncological diseases in St. Petersburg, Russia /P. Kolpak, I.S. Frantsuzova, E.O. Evmenova // Drug Invention Today. - 2019. - V. 11 (3). – P. 510-516.
24. Kim E. Adaptive therapy for metastatic melanoma: Predictions from patient calibrated mathematical models / Kim J.S. Brown, et al. // Cancers February - 2021. - V. 13(4). – P. 1-15. DOI: 10.3390/cancers13040823.

Список литературы на английском языке / References in English

1. The State of Cancer Care Provided to the Population of Russia in 2018. Moscow: FSBI P.A. Herzen Moscow Cancer Research Institute, Branch Office of FSBI NMRRC, Ministry of Health of Russia; 2018. p. 236. [Electronic resource]. URL: https://nnood.ru/wp-content/uploads/2019/04/Statichticheskijj-ezhegodnik-Gercena-2018.pdf. (accessed: 12.06.2021)
2. Zakurdyaeva I.G. The treatment of patients with late relapses of skin melanoma with isolated metastatic regional lymph nodes involvement / I.G. Zakurdyaeva, A.F. Tsyb, V.S. Parshin et al. // Voprosy Onkologii. - 2012. - V. 58 (3). - P. 402-405.
3. Ruksha T. G. High throughput analysis of single cancer cells as the basis for personalized therapy of oncological diseases / T. G. Ruksha, E. Yu. Sergeeva, A. V. Komina // Tsitologiia. - - V. 59 (10). - P. 654-661.
4. Burov D.A. Klinika Pervichno-mnozhestvennaja melanoma kozhi. Klinicheskij sluchaj [Clinical Picture of Primary Multiple Melanoma of the Skin. Clinical Case] / D.A. Burov, Ja.A. Bozhchenko, A.A Tararykova et al. // Sarkomy kostej, mjagkih tkanej i opuholi kozhi [Sarcomas of Bones, Soft Tissues and Skin Tumors]. - 2016. - № 1. - pp. 76-80. [in Russian]
5. Kopnin B.P. Genome instability and oncogenesis /P. Kopnin // Molecular Biology. - 2007. - V. 41 (2). - P. 329-339.
6. Cle´ment Chatelain, Pasquale Ciarletta, Martine Ben Amar Morphological changes in early melanoma evelopment:Influence of nutrients, growth inhibitors and cell-adhesion mechanisms // Journal of Theoretical Biology. - 2011. - V. 290. - P. 46–59. DOI:10.1016/j.jtbi.2011.08.029.
7. Snarskaja E.S. Bespigmentnaja uzlovaja melanoma kozhi goleni [Pigmentless Nodular Melanoma of the Shin Skin] / E.S. Snarskaja, K.M. Avetisjan, V.V. Andrjuhina // Rossijskij zhurnal kozhnyh i venericheskih boleznej [Russian Journal of Skin and Venereal Diseases]. - 2014. - № 2. - pp. 4-7. [in Russian]
8. Procenko A. Targetnaja terapija pri melanome, gastrointestinal'nyh stromal'nyh opuholjah, dermatofibrosarkome protuberans [Targeted Therapy for Melanoma, Gastrointestinal Stromal Tumors, Dermatofibrosarcoma Prominence] / Procenko // Prakticheskaja onkologija [Practical Oncology]. - 2010. - Vol. 11. - №3. – pp. 1262-170. [in Russian]
9. Tsur N. Response of patients with melanoma to immune checkpoint blockade –insights gleaned from analysis of a new mathematical mechanistic model / N. Tsur, Y. Kogan, M. Rehm et al. // Journal of Theoretical Biology. - 2020. - V. 485. № 110033. DOI: 10.1016/j.jtbi.2019.110033.
10. Chu E. Physicians cancer chemotherapy drug manual / E. Chu, V.T. DeVita // Jones and Bartlett publishers. Boston, USA. 2007.
11. Zakurdjaeva I.G., Cyb A.F. Metastaticheskaja melanoma kozhi (obzor literatury) [Metastatic Skin Melanoma (Literature Review)] / I.G. Zakurdjaeva, A.F. Cyb // Sibirskij onkologicheskij zhurnal [Siberian Oncological Journal]. - 2010. - №6 (42). - pp. 56-62. [in Russian]
12. Byrne H.M. The role of cell-cell interactions in a two-phase model for avascular tumour growth / H.M. Byrne, J.W. Breward, C.E. Lewis // Journal of Mathematical Biology. - 2001. - V. 45 (2). - P. 125 – 131.
13. Haridas P. Quantifying rates of cell migration and cell proliferation in co-culture barrier assays reveals how skin and melanoma cells interact during melanoma spreading and invasion / Parvathi Haridas, Catherine J. Penington, Jacqui A. McGovern et al. // Journal of Theoretical Biology. - 2017. - V. 423. - P. 13–25.
14. Albano G. Estimating and determining the effect of a therapy on tumor dynamics by means of a modified Gompertz diffusion process / Giuseppina Albano, Virginia Giorno, Patricia Román-Román et al. // Journal of Theoretical Biology. - 2015. - V. 364. - P. 206–219.
15. Akhmetzhanov A.R. Modelling bistable tumour population dynamics to design effective treatment strategies / Andrei R. Akhmetzhanov, Jong Wook Kim, Ryan Sullivan et al. // Journal of Theoretical Biology. - 2019. - V. 474. - P. 88–102. DOI: 10.1016/j.jtbi.2019.05.005.
16. Procenko S.A. Melanoma kozhi: novoe v lekarstvennom lechenii [Skin Melanoma: New in Drug Treatment] / A. Procenko // Priroda [Nature]. - 2018. - № 6. - pp. 26-28. [in Russian]
17. Palkina, N.V. Prooncogenic effects of inhibiting the microRNA miR-106A in skin melanoma cells in vitro /V. Palkina, A.V. Komina, M.B. Aksenenko, et al. // Tsitologiia. - 2016. - V. 58 (9). - P. 679-687.
18. Rommelfanger D.M. Dynamics of melanoma tumor therapy with vesicular stomatitis virus: explaining the variability in outcomes using mathematical modeling / D.M. Rommelfanger, C.P. Offord, J. Dev et al. // Gene Therapy. - 2012. - V. 19. - 543–549.
19. Goncharova A.B. Matematicheskoe modelirovanie lechenija onkologicheskogo zabolevanija [Mathematical Modeling of Cancer Treatment] / A.B. Goncharova, E.P. Kolpak, M.M. Rasulova et al. // Vestnik Sankt-Peterburgskogo universiteta. Prikladnaja matematika. Informatika. Processy upravlenija. [Bulletin of the Saint Petersburg University. Applied Mathematics. Computer Science. Management Processes.] 2020. Vol. 16. № 4. pp. 437-446 DOI: 10.21638/11701/SPBU10.2020.408. [in Russian]
20. Goncharova A.B. Postanovka predvaritel'nogo medicinskogo diagnoza na osnove teorii nechetkih mnozhestv s ispol'zovaniem mery Sugeno [Making a Preliminary Medical Diagnosis Based on the Theory of Fuzzy Sets Using the Sugeno Measure] / A.B. Goncharova // Vestnik Sankt-Peterburgskogo universiteta. Prikladnaja matematika. Informatika. Processy upravlenija. [Bulletin of the Saint Petersburg University. Applied Mathematics. Computer Science. Management Processes.] 2019. Vol. 15. № 4. pp. 529-543. DOI: 10.21638/11702/spbu10.2019.409. [in Russian]
21. Tarkov S.A. Osobennosti techenija melanom kozhi golovy i shei [Features of the Course of Melanomas of the Scalp and Neck] / S.A. Tarkov, A.E. Mihnin, K.V. Shelehova // Voprosy onkologii [Issues of Oncology]. - 2013. – Vol. 59. - № 1. - 114-117. [in Russian]
22. Mjasnjankin M.Ju. Podnogtevaja melanoma [Subungual Melanoma] / M.Ju. Mjasnjankin, G.I. Gafton, V.V. Anisimov et al. // Jeffektivnaja farmakoterapija [Effective Pharmacotherapy]. - 2016. - Vol. 39. - pp. 40-44. [in Russian]
23. Kolpak E.P. Oncological diseases in St. Petersburg, Russia /P. Kolpak, I.S. Frantsuzova, E.O. Evmenova // Drug Invention Today. - 2019. - V. 11 (3). – P. 510-516.
24. Kim E. Adaptive therapy for metastatic melanoma: Predictions from patient calibrated mathematical models / Kim J.S. Brown, et al. // Cancers February - 2021. - V. 13(4). – P. 1-15. DOI: 10.3390/cancers13040823.