СИММЕТРИЧЕСКАЯ ГРУППА И ЕЕ ГЕНЕТИЧЕСКИЙ КОД
СИММЕТРИЧЕСКАЯ ГРУППА И ЕЕ ГЕНЕТИЧЕСКИЙ КОД
Научная статья
Казинец В.А. *
Тихоокеанский государственный университет, Хабаровск, Россия
* Корреспондирующий автор (kazinec[at]khspu.ru)
АннотацияОписание генетического кода симметрической группы. Предложен новый подход к построению генетических кодов симметрической группы. На основании данного подхода получено однозначное представление элементов группы в виде произведения циклов. Используя такое представление, изучены некоторые свойства группы Sn. Представление элементов группы в виде одночлена позволяет построить ортогональные базисы в пространстве комплекснозначных функций на группе.
Ключевые слова: Симметрическая группа, генетический код, подгруппы.
SYMMETRIC GROUP AND ITS GENETIC CODE
Research article
Kazinets V.A. *
Pacific State University, Khabarovsk, Russia
* Corresponding author (kazinec[at]khspu.ru)
AbstractThe article contains the description of the genetic code of the symmetric group. A new approach to the construction of the genetic codes of the symmetric group is proposed. Based on this approach, an unambiguous representation of the elements of the group in the form of a product of cycles is obtained. Using this representation, we studied some properties of the Sn group. The representation of the elements of the group as a monomial allows constructing orthogonal bases in the space of complex-valued functions on the group.
Keywords: Symmetric group, genetic code, subgroups.
Введение
Симметрическая группа играет существенную роль в теории групп, так как любая конечная группа является ее подгруппой, при этом на представлениях этой группы во многом базируются представления классических матричных групп, подгруппа четных перестановок является группой Вейля. Неприводимые представления Sn обычно описывают с помощью диаграмм и таблиц Юнга [2], что приводит к серьезным комбинаторным сложностям, рассматривать функции с аргументом в виде таблиц Юнга не очень удобно. Мы предлагаем другой подход к описанию группы Sn, который позволит однозначно представить элементы группы в виде одночлена.
![]()
Накладывая условия на степени данного одночлена, получим подгруппы симметрической группы. Заметим, что комплеснозначные функции на группе являются периодическими функциями от n-1 переменной с периодом T=i+1 по i-той переменной, что позволит построить ортогональный базис.
Обычно, конечная группа задается таблицей Кэли, но когда порядок группы достаточно велик, эту таблицу затруднительно выписать в явном виде. Описание групп с указанием множества порождающих элементов и множества определяющих соотношений между порождающими элементами, имеющее название копредставление или генетический код, является более компактным методом описания конечных групп. Такое описание позволяет описать некоторые свойства группы и элементов группы, но мало что говорит о строении самой группы.
Первые определения, теоремы и проблемы теории групп, возникшие в трудах Лагранжа, Абеля и Галуа, относились к группам перестановок (симметрической группе). В соответствии с теоремой Кэли, любая конечная группа изоморфна некоторой подгруппе группы перестановок, что указывает на значимость симметрической группы в теории групп.
Существует достаточно много генетических кодов группы ![]() [8], [9].
[8], [9].
- Код Бернсайда
![]()
в порождающих ![]() . Данный код содержит лишние соотношения.
. Данный код содержит лишние соотношения.
- Код Мура
Мур указал и следующий код
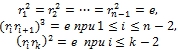
В порождающих ![]()
В настоящее время наиболее часто используется следующее представление
![]()
В работах [1],[3],[4] предложен генетический код симметрической группы, определяемый тождествами:
![]() (1)
(1)
В настоящей работе предлагается возможность получить набор генетических кодов, позволяющих исследовать структуру симметрической группы.
Основные результаты
Теорема 1. Пусть ![]() порождающие группы, тогда тождества
порождающие группы, тогда тождества
![]() (2)
(2)
Являются генетическим кодом группы ![]()
Доказательства: Обозначим через ![]()
То есть тождества (2) порождают тождества (1).
Обратно, пусть ![]()
![]()
Тождества (1) порождают тождества (2),что и доказывает теорему.
Теорема 2. Любой элемент ![]() однозначно представим в виде
однозначно представим в виде
![]()
Рассмотрим действие элемента ![]() на множестве {0,1,2,…,n-1}, обычно элемент представляют в виде перестановки
на множестве {0,1,2,…,n-1}, обычно элемент представляют в виде перестановки
Теорема 3. Имеет место равенство
![]() , где - остаток от деления числа x на k.
, где - остаток от деления числа x на k.
Для доказательства данного утверждения достаточно заметить, что ![]() - это цикл (0,1,2,…,i-1), а
- это цикл (0,1,2,…,i-1), а ![]() сдвиг цикла на
сдвиг цикла на ![]() по модулю i+1.
по модулю i+1.
Обратная задача решается несколько сложнее, раскрывая равенства из теоремы 3, мы получим систему уравнений, исключая промежуточные переменные получим следующий результат.
Теорема 4.Пусть задана перестановка ![]() , тогда степени
, тогда степени 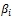 , элемента
, элемента ![]() являются решением системы линейных уравнений
являются решением системы линейных уравнений
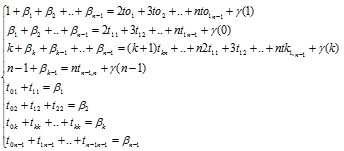
Все величины в системе неотрицательные целые числа, при этом ![]() ,
,
Теорема 3 позволяет сформулировать следующее утверждение
Замечание. Пусть дан набор чисел ![]() , удовлетворяющих условиям
, удовлетворяющих условиям
![]()
![]() тогда
тогда ![]() порождающие элементы группы
порождающие элементы группы ![]() тождества между которыми легко получить используя формулы (2).Полученные генетические коды позволяют описать некоторые подгруппы симметрической группы. Например:
тождества между которыми легко получить используя формулы (2).Полученные генетические коды позволяют описать некоторые подгруппы симметрической группы. Например:
а) Элемент ![]() принадлежит
принадлежит ![]() , подгруппе четных перестановок, тогда и только тогда, когда
, подгруппе четных перестановок, тогда и только тогда, когда
![]()
б) Множество элементов ![]() , удовлетворяющих условиям
, удовлетворяющих условиям
![]()
образуют подгруппу изоморфную ![]() .
.
Так как ![]() , то функции на группе
, то функции на группе![]() являются периодическими с периодом i+1 по i-той переменной. То есть, если
являются периодическими с периодом i+1 по i-той переменной. То есть, если ![]() , то
, то
![]()
Теорема. Пусть набор целых чисел ![]() удовлетворяет условию
удовлетворяет условию ![]() , тогда множество функций
, тогда множество функций
![]()
образует ортогональный базис в пространстве комплекснозначных функций на группе ![]() относительно стандартного скалярного произведения
относительно стандартного скалярного произведения ![]()
Поставим каждому элементу ![]() в соответствие целое число
в соответствие целое число
![]()
Легко показать, что данное соответствие является взаимно-однозначным. То есть группа ![]() взаимно-однозначно отображается на множестве целых чисел отрезка
взаимно-однозначно отображается на множестве целых чисел отрезка ![]() , тогда функцию
, тогда функцию ![]() можно рассматривать как функцию
можно рассматривать как функцию ![]() .
.
Теорема. Пусть ![]() , m- целое. Тогда функции
, m- целое. Тогда функции ![]() , образуют ортогональный базис в пространстве комплекснозначных функций на группе
, образуют ортогональный базис в пространстве комплекснозначных функций на группе ![]() .
.
Заключение. Полученные результаты позволяют перейти к изучению свойств симметрической группы, описанию ее подгрупп, рассмотрению функций, определяющих умножение в группе [4], описанию сопряженных элементов, построению неприводимых представлений симметрической группы без использования диаграмм Юнга. Обратим внимание на интересные тождества, получаемые при описании группы в терминах одночленов
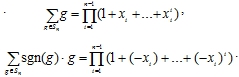
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Cписок литературы / References
- Богоутдинов Д. Г. Свойства операции умножения в группе / Д. Г. Богоутдинов // XXXIV Дальневосточная математическая школа-семинар им. ак. Е. В. Золотова «Фундаментальные проблемы математики и информационных наук»: тез. докл. – Хабаровск: Изд-во Тихоокеан. гос. ун-та, 2009. – С. 10-12.
- Джеймс Г. Теория представлении симметрических групп: пер. с англ. / Г. Джеймс. – М. : Мир, 1982. – 216 с.
- Казинец В. А. Копредставление симметрической группы / В. А. Казинец // XXXIV Дальневосточная математическая школа-семинар им. ак. Е. В. Золотова «Фундаментальные проблемы математики и информационных наук»: тез. докл. – Хабаровск: Изд-во Тихоокеан. гос. ун-та, – 2009. – С. 33-35.
- Казинец В. А. Умножение в симметрической группе, заданной генетическим кодом / В. А. Казинец // Действие торов: топология, геометрия, теория чисел: тезисы докладов Международной открытой российско-китайской конференции, Хабаровск, 2-7 сентября 2013 г. / под научной ред. Бухштабера В. М., Быковского В. А. – Хабаровск: Изд-во Тихоокеан. гос. ун-та, – – С. 89-90.
- Казинец В. А. Умножение в конечных группах, заданных генетическим кодом / В. А. Казинец, А.Ю. Разумовская // Научно-образовательный журнал «Вестник Приамурского государственного университета им. Шолом-Алейхема»/ Биробиджан: Изд-во ФГБОУВПО «ПГУ им.Шолом-Алейхема», – – №4(17).– С. 83-86.
- Казинец В. А. Некоторые свойства группы ,заданной генетическим кодом / В.А. Казинец, И.Ю. Духовникова // Интеграция науки и практики в современных условиях : Материалы XII Международной научно-практической конференции (19 июня 2018г.): сборник научных трудов / Научный ред. канд. техн. наук, доц. Цечоева А.Х.- М.:Издательство «Перо», 2018. – С.63-65.
- Казинец В. А. Некоторые свойства группы ,заданной генетическим кодом / В.А. Казинец, И.Ю. Духовникова // Интеграция науки и практики в современных условиях : Материалы XII Международной научно-практической конференции (19 июня 2018г.): сборник научных трудов / Научный ред. канд. техн. наук, доц. Цечоева А.Х.- М.:Издательство «Перо», 2018. – С.63-65.
- Коксетер Г. С. М. Порождающие элементы и определяющие соотношения дискретных групп: пер. с англ. / Г. С. М. Коксетер, У. О. Дж. Мозер; под ред. Ю. И. Мерзлякова. – М.: Наука, – 1980. – 240с.
- Магнус В. Комбинаторная теория групп. Представление групп в терминах образующих и соотношений / В. Магнус, А. Каррас, Д. Солитэр; пер. с англ. Д. И. Молдаванского, А. А. Фридмана, Ю. И. Хмелевского; под ред. М. Д. Гриндлингера. – М.: Наука, 1974. – 456с.
Список литературы на английском языке / References in English
- Bogoutdinov D. G. vojstva operacii umnozheniya v gruppe [Properties of multiplication operations in a group] / D. G. Bogoutdinov // XXXIV Dal'nevostochnaya matematicheskaya shkola-seminar im. ak. E. V. Zolotova «Fundamental'nye problemy matematiki i informacionnyh nauk [XXXIV Far-Eastern Mathematical School-Seminar named after. ac EV Zolotov, “Fundamental Problems of Mathematics and Information Sciences”]: mes. report - Khabarovsk: Pacific Publishing House. state University, 2009. - p. 10-12.
- James G. Teoriya predstavlenii simmetricheskih grupp [Theory of Representation of Symmetric Groups]: Per. from English / G. James. - M.: Mir, 1982. - 216 p.
- Kazinets V. A. Kopredstavlenie simmetricheskoj gruppy [Copresentation of a symmetric group] / V. A. Kazinets // XXXIV Dal'nevostochnaya matematicheskaya shkola-seminar im. ak. E. V. Zolotova «Fundamental'nye problemy matematiki i informacionnyh nauk [XXXIV Far-Eastern Mathematical School-Seminar. ac EV Zolotov, “Fundamental Problems of Mathematics and Information Sciences”]: mes. report - Khabarovsk: Pacific Publishing House. state University, - 2009. - p. 33-35.
- Kazinets V. A. Umnozhenie v simmetricheskoj gruppe, zadannoj geneticheskim kodom [Multiplication in the symmetric group given by the genetic code] / V. A. Kazinets // Dejstvie torov: topologiya, geometriya, teoriya chisel: tezisy dokladov Mezhdunarodnoj otkrytoj rossijsko-kitajskoj konferencii [Action of tori: topology, geometry, number theory: abstracts of the International Open Russian-Chinese Conference], Khabarovsk, 2-7 September 2013 city / under scientific ed. Buchstaber V.M., Bykovsky V.A. - Khabarovsk: Pacific Publishing House. state University, - 2013. - p. 89-90.
- Kazinets V. A. Umnozhenie v konechnyh gruppah, zadannyh geneticheskim kodom [Multiplication in finite groups defined by the genetic code] / V. A. Kazinets, A. Yu. Razumovskaya // Nauchno-obrazovatel'nyj zhurnal «Vestnik Priamurskogo gosudarstvennogo universiteta im. SHolom-Alejhema [Scientific and educational journal "Bulletin of the Amur State University. Sholem Aleichem "] / Birobidzhan: Publishing House of FSBEI HPE" PSU them. Sholem Aleichem ”, - 2014. - №4 (17) .– P. 83-86.
- Kazinets, V. A. Nekotorye svojstva gruppy ,zadannoj geneticheskim kodom [Some properties of a group given by a genetic code] / V.A. Kazinets, I.Yu. Dukhovnikova // Integraciya nauki i praktiki v sovremennyh usloviyah : Materialy XII Mezhdunarodnoj nauchno-prakticheskoj konferencii (19 iyunya 2018g.): sbornik nauchnyh trudov [Integration of science and practice in modern conditions: Proceedings of the XII International Scientific and Practical Conference] (June 19, 2018): collection of scientific papers / Scientific Ed. Cand. tech. Sciences, Assoc. Tsechoev A.Kh.- M.: Perot Publishing House, 2018. - P.63-65.
- Kazinets V. A. ekotorye svojstva gruppy, zadannoj geneticheskim kodom [Some properties of a group given by a genetic code] / V.A. Kazinets, I.Yu. Dukhovnikova // Integraciya nauki i praktiki v sovremennyh usloviyah : Materialy XII Mezhdunarodnoj nauchno-prakticheskoj konferencii (19 iyunya 2018g.): sbornik nauchnyh trudov [Integration of science and practice in modern conditions: Proceedings of the XII International Scientific and Practical Conference (June 19, 2018)]: collection of scientific papers / Scientific Ed. Cand. tech. Sciences, Assoc. Tsechoev A.Kh.- M.: Perot Publishing House, 2018. - P.63-65.
- Coxeter, G.S.M. Porozhdayushchie elementy i opredelyayushchie sootnosheniya diskretnyh grupp: per. s angl [The generating elements and the defining relations of discrete groups: Per. from English] / G.S.M. Coxeter, W. O. J. Moser; by ed. Yu. I. Merzlyakov. - M .: Science, - 1980. - 240s.
- Magnus V. Kombinatornaya teoriya grupp. Predstavlenie grupp v terminah obrazuyushchih i sootnoshenij [Combinatorial group theory. Representation of groups in terms of generators and relations] / V. Magnus, A. Karras, D. Solitaire; per. from English D.I. Moldavansky, A.A. Fridman, Yu.I. Khmelevsky; by ed. Md grindlinger - M .: Science, 1974. - 456s.
