СОЗДАНИЕ СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ ДЛЯ ИЗУЧЕНИЯ ЭФФЕКТОВ ВОЛНОВОЙ ОПТИКИ

СОЗДАНИЕ СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ ДЛЯ ИЗУЧЕНИЯ ЭФФЕКТОВ ВОЛНОВОЙ ОПТИКИ

Научная статья

Минченко И.И.¹, Козий А.А.^2, *, Ларин Р.С.³

¹ ORCID: 0000-0001-8895-4850, Московский государственный технический университет им. Н.Э. Баумана, Москва, Россия;

² ORCID: 0000-0003-0063-5834,

Московский государственный технический университет им. Н.Э. Баумана, Москва, Россия;

³ ORCID: 0000-0003-1913-2911,

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» имени В.И. Ульянова (Ленина), Санкт-Петербург, Россия

* Корреспондирующий автор (kiborgiii[at]mail.ru)

Аннотация

Настоящая работа посвящена созданию системы автоматизированного проектирования «Оптический конструктор». В программу заложены физические основы волновой оптики. Основной решаемой задачей конструктора является построение интерференционной картины от проходящего через различные элементы лазерного пучка. Смоделированы такие оптические установки, как интерферометр Маха-Цендера и «Квантовый ластик». В программе возможно создание оптических схем произвольной сложности с использованием одного элемента «Лазер» и произвольного числа остальных элементов (в том числе и элементов «Экран»).

Ключевые слова: поляризация, моделирование, волновая оптика, интерферометр Маха-Цендера, «квантовый ластик».

DEVELOPMENT OF AUTOMATED DESIGN SYSTEM FOR STUDYING WAVE OPTICS EFFECTS

Research article

Minchenko I.I.¹, Koziy A.A.^2, *, Larin R.C.³

¹ ORCID: 0000-0001-8895-4850,

Bauman Moscow State Technical University, Moscow, Russia;

² ORCID: 0000-0003-0063-5834,

Bauman Moscow State Technical University, Moscow, Russia;

³ ORCID: 0000-0003-1913-2911,

St. Petersburg State Electrotechnical University, Saint Petersburg, Russia

* Corresponding author (kiborgiii[at]mail.ru)

Abstract

This work is devoted to the development of "Optical Designer" – the computer design system. The program includes the physical fundamentals of wave optics. The main task of the designer is to construct an interference pattern from a laser beam passing through various elements. Optical devices such as the Mach-Zehnder interferometer and the "Quantum eraser" are simulated. The program enables to create optical circuits of arbitrary complexity using one "Laser" element and an arbitrary number of other elements (including the "Screen" elements).

Keywords: polarization, modeling, wave optics, Mach-Zehnder interferometer, "quantum eraser".

Введение

В настоящее время существует множество профессиональных программ для моделирования оптических эффектов (например, VirtualLab Fusion). Эти программы являются достаточно сложными, что сильно затрудняет получение результатов для малоопытных пользователей. Для обучения студентов технических специальностей физическим основам волновой оптики была разработана система автоматизированного проектирования «Оптический конструктор». В данной программе возможно создание многоэлементных оптических схем без использования большого числа обязательных настроек, что позволяет пользователям без особых временных затрат получать желаемые результаты. Программа позволяет на качественном уровне рассмотреть предполагаемые эффекты в созданной установке. Что актуально для студентов, в дальнейшем возможно сравнить результаты с реальными оптическими лабораторными установками. При отсутствии достаточно дорогого оптического оборудования возможен полный переход в лабораторных работах на программу «Оптический конструктор».

Физические основы

Для подробного рассмотрения системы автоматизированного проектирования «Оптический конструктор» необходимо начать с заложенной в него физической модели. Основным рассматриваемым объектом является свет. Свет описывается поперечной волной, которая распространяется вдоль вектора , а векторы электрической напряженности  и магнитной индукции  колеблются в плоскости, перпендикулярной направлению распространения. Между векторами  и  имеется однозначная взаимосвязь, поэтому в дальнейшем будем рассматривать только колебания вектора напряженности  [1]. Напряженность электрического поля плоской волны, распространяющейся вдоль оси z имеет вид [2]:

где  – вектор напряженности электрического поля в точке  в момент времени t,  – единичный вектор поляризации, лежащий в плоскости xy, E₀ – комплексная амплитуда волны, k – волновое число, ω – циклическая частота.

В оптической установке для получения интерференционной картины необходимо, чтобы падающие на любой элемент волны были когерентными. Это возможно при условии наличия единственного лазера. Таким образом, экспоненциальный член  сократится при расчете интенсивности на экране, а значит его можно опустить из рассмотрения [3]. В приведенной модели плоская волна может быть описана с использованием двух комплексных чисел – «комплексных поляризаций» по осям х и у:

Все элементы оптической системы описываются линейными операторами, которые могут быть записаны в виде матриц. Матрица оператора действует на вектор столбец, состоящий из комплексных поляризаций приходящего света, и результатом операции является вектор столбец, состоящий из комплексных поляризаций выходящего света. Размер матрицы зависит от числа входов и выходов элемента. В программе реализованы такие элементы как «Лазер», «Поляризатор», «Полупрозрачное зеркало», «Поляризационный светоделитель», «Пластинки », «Линия задержки», «Интерферометр Майкельсона» и «Экран». Самым сложным элементом «Оптического конструктора» является «Экран».

Далее будут рассмотрены три элемента – «Поляризатор», «Полупрозрачное зеркало» и «Экран».

Поляризатор

«Поляризатор» – это элемент, который имеет один вход и один выход (рис. 1). Поляризатор делает произвольную световую волну плоско-поляризованной в направлении, определяемом углом самого поляризатора  [4].

Рис. 1 – Изображение элемента «Поляризатор»

Примечание: кружком обозначается входной слот, а треугольником – выходной  

Оператор элемента представляет собой матрицу размера , так как входящий и выходящий свет описывается как вектор столбец размера :

где  – приходящая волна, а   – выходящая.

Полупрозрачное зеркало

«Полупрозрачное зеркало» (ППЗ) – это элемент, который имеет два входа и два выхода (рис. 2). По одному выходному направлению ППЗ суммирует две приходящие волны, а по другому направлению даёт их разность [5].

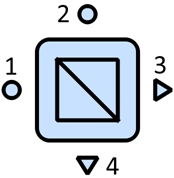
Рис. 2 – изображение элемента «Полупрозрачное зеркало»

 

В представленной модели две входящие волны не суммируются (вычитаются), а подаются на выход как список независимых волн, что соответствует принципу суперпозиции. Это позволяет в дальнейшем ввести модель неидеальной юстировки приборов для более точного вычисления интерференционных картин на экране. Входящий в элемент свет описывается как вектор столбец размером  (два входа), а выходящий как вектор столбец размером  (два выхода, и на каждом список из двух волн). Таким образом, матрица оператор имеет размер :

где А₁ и А₂ – приходящие волны, а А₃ и А₄ – выходящие.

Экран

«Экран» – это элемент, который имеет один вход. На нем происходит сложение приходящего списка волн и расчет с последующей визуализацией в отдельном окне графика интенсивности.

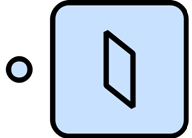
Рис. 3 – изображение элемента «Экран»

 

Для наблюдения интерференционной картины необходимо, чтобы приходящие на экран волны были не параллельными, а располагались под малым углом друг к другу [6]. Именно в этом элементе необходимо вносить поправку на не идеальность юстировки приборов. Для добавления данной поправки была разработана следующая модель. Пусть на экран приходит список волн, который не несет информации о их взаимном расположении. В рамках модели полагается, что волны приходят на экран под одинаковыми углами между соседями. Этот угол задается в программе через функцию f и параметр , который влияет на период интерференционной картины.

                                                                а)                                                                                     б)

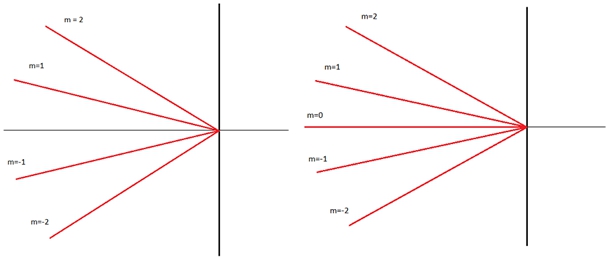
Рис. 4 – Модель приходящих на экран волн:

а) четного числа; б) нечетного числа

В рамках приведенной модели j – я волна, приходящая на экран, будет записываться следующим образом:

где  – вектор комплексной поляризации,  – функция, определяющая угол падения j-й волны на экран,  – волновой вектор, который направлен вдоль экрана по направлению .

Функция  зависит от количества приходящих волн n (четное или нечетное), и в логическом виде записывается следующим образом:

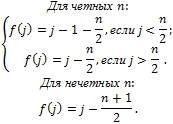
Для вычисления интенсивности света на экране необходимо произвести суммирование всех приходящих волн (с учетом параметров отклонений):

где  – электрическая постоянная, c – скорость света, .

Интенсивность может быть разложена на две независимые компоненты – x и y [7]. Это позволит упростить вычисления:

Интенсивность по одному из направлений (пусть будет x) может быть выражена следующим образом:

где 

Подставляя значения  получаем следующее уравнение:

Аналогичное выражение будет и для у - составляющей. Данный вид уравнения для интенсивности позволяет на качественном уровне проанализировать характер интерференционной картины по наличию в формуле косинусов и синусов и стоящих в них величинах.

Условия нормировки и затухания интенсивности света на экране

Для получения физически-верных результатов интенсивности на экране необходимо найти значение напряженности выходящего света из лазера. Эта величина может быть получена из интенсивности лазерного пучка. За базовый параметр была взята интенсивность равная . Тогда напряженность электрического поля может быть вычислена из следующих уравнений:

где  – комплексная напряженность электрического поля лазера. Предполагается, что свет обладает диагональной поляризацией, тогда вектор напряженности можно записать в следующем виде:

Пусть , что соответствует диагональной поляризации, тогда: где параметр α вычисляется следующим образом:

Более реалистичная эмуляция обеспечится путем добавления эффекта затухания интенсивности света на экране. Размер экрана был принят равным 100 мм, причем размер хорошо наблюдаемой интерференционной картины составляет около 50 мм (считается, что в реальной установке такие размеры интерференционных картин соответствовали бы постановке увеличительной линзы). Для этого вводится искусственное домножение вычисленной интенсивности на следующую функцию:

где l – отклонение от центра экрана, σ – расстояние от центра, на котором интенсивность света упадет в e раз. Для моделирования был выбран параметр 

Расчет интенсивности производится только для оси l, в связи с чем необходимо перенормировать интенсивность на одну ось и учитывать рассеивание пучка линзой. Энергия, которую несет лазерный пучок – 1000 мВт (в стандартных настройках), распределяется по всей ширине экрана в соответствии с функцией φ, причем  – если энергия излучения не теряется в элементах системы (например, в поляризаторах), тогда суммарная энергия света на экране равняется энергии лазерного пучка. Таким образом, интенсивность на экране обладает размерностью .

Для получения удобных для анализа интерференционных картин необходимо подобрать угол (параметр ), под которым две волны падают друг относительно друга. Пусть на полном экране укладывается 10 колебаний с самым высоким периодом (что соответствует величинам, стоящим в функциях  в уравнении для интенсивности). Тогда параметр отклонения  можно найти следующим образом:

где N – число периодов на экране,  – размер экрана.

Примеры собранных экспериментальных установок

Для примера работы программы были выбраны следующие установки – «Интерферометр Маха-Цендера» и «Квантовый ластик». Эти установки просты как в реальной, так и в программной реализации, и позволяют оценить работоспособность программы.

Интерферометр Маха-Цендера

Интерферометр Маха-Цендера состоит из двух полупрозрачных зеркал (ППЗ) и двух обычных зеркал. Луч света разделяется на первом ППЗ, перенаправляется на зеркалах, и собирается на втором ППЗ. Из-за того, что два пучка света из плеч интерферометра пришли под малым углом относительно друг друга, то на выходе из интерферометра будет наблюдаться интерференционная картина [8]. В представленной программе элемент «Зеркало» отсутствует из-за отсутствия необходимости, поэтому интерферометр «Маха-Цендера» реализуется на двух ППЗ (рис. 5). В плечи интерферометра можно внести такой элемент как «Линия задержки», это сдвинет интерференционную картину на экране на соответствующую величину задержки (рис. 6).

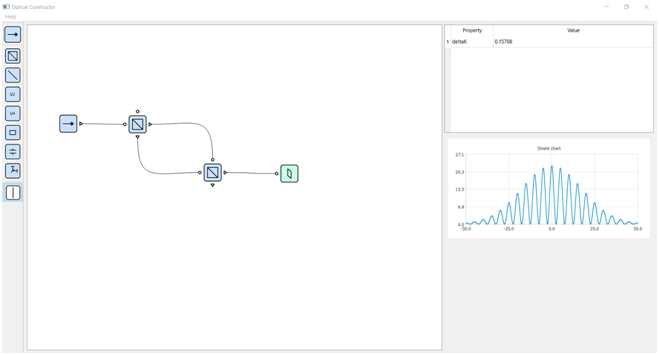
Рис. 5 – Модель установки «Интерферометр Маха-Цендера»

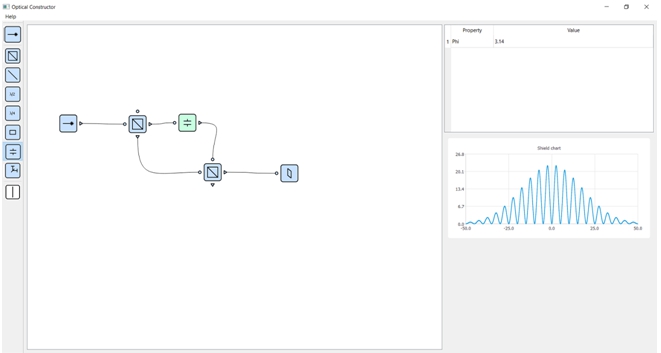
Рис. 6 – Модель установки «Интерферометра Маха-Цендера» с линией задержки в верхнем плече

 

Эксперимент «Квантовый ластик»

Экспериментальная установка «Квантовый ластик» подробно описана в работе [9], и является переделанной установкой интерферометра «Маха-Цендера». Установка состоит из одного поляризационного светоделителя, одного ППЗ, двух зеркал и трех поляризаторов (в нашей программе отсутствуют два зеркала и вместо трех поляризаторов используется один). Свет от лазера проходит через диагональный поляризатор (в программной реализации диагональную поляризацию можно задать в настройках излучения самого лазера) и попадает в поляризационный светоделитель, затем разделяется на два направления и собирается на ППЗ. После ППЗ свет проходит через второй поляризатор, и, в зависимости от установленной плоскости поляризации, может наблюдаться интерференционная картина на экране. При горизонтальной или вертикальной ориентации плоскости поляризации интерференционной картины наблюдаться не будет (рис. 7), а при диагональной наблюдается наиболее выраженная интерференционная картина (рис. 8).

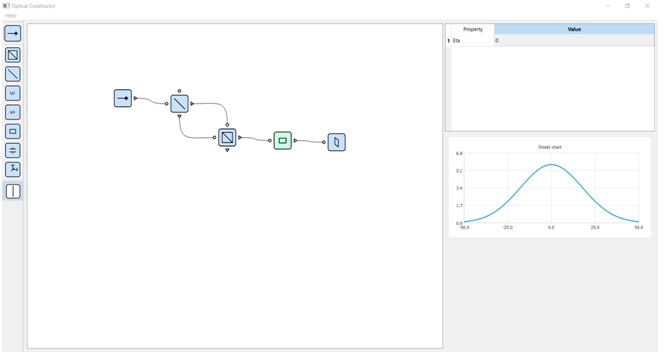
Рис. 7 – Модель установки «Квантовый ластик» с горизонтальным поляризатором

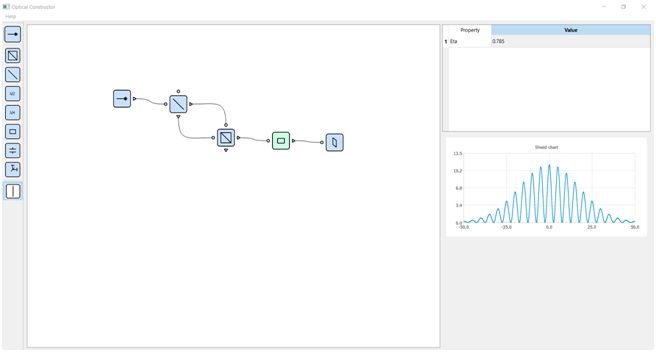
Рис. 8 – Модель установки «Квантовый ластик» с диагональным поляризатором

 

Заключение

В результате работы была создана программа, в которой моделируются эффекты волновой оптики. Система автоматизированного проектирования «Оптический конструктор» несет в себе образовательную цель, так как обладает достаточно простым и интуитивно понятным интерфейсом, и наглядно показывает эффекты волновой оптики, например, такие как поляризация и интерференция. Программа, а также более подробное математическое описание доступно по ссылке [10]. В дальнейшем планируется добавление встроенных обучающих лабораторных работ по теме «Волновая оптика» для студентов технических специальностей, системы справок, и готовых моделей физических установок с теоретическим описанием эффектов.

Благодарности Авторы работы выражают глубокую благодарность Киктенко Е.О. за наставления и ценные комментарии в процессе выполнения работы, а также Скуйбину Б.Г. и Морозову А.Н. за предоставленную возможность выполнения работы в рамках проекта студенческой экспериментальной лаборатории физики (СЭЛФ) МГТУ им. Н.Э. Баумана.	Acknowledgement The authors of the paper express their deep gratitude to E.O. Kiktenko for instructions and valuable comments during the process of execution of work, and also to Skuibin B.G. and Morozov A.N. for the given opportunity to perform work in the framework of the project of the student experimental physics laboratory (SELF) in Bauman Moscow State Technical University.
Конфликт интересов Не указан.	Conflict of Interest None declared.

Список литературы / References

1. Мартинсон Л. К. Электромагнитное поле : учеб. пособие / Л. К. Мартинсон, А. Н. Морозов, Е. В. Смирнов. – М. : Изд-во МГТУ им. Н.Э. Баумана, 2013. – 422 c.
2. Фейнман Р. Фейнмановские лекции по физике. В 10 ч. Ч. 6. Электродинамика. / Р. Фейнман, Р. Лейтон, М.Сэндс. – М. : Эдиториал УРСС 2004. – 339 с.
3. СивухинД.В. Оптика / Д.В Сивухин. – 3-е изд. – М. : Физматлит, 2005. – 792 с.
4. Иродов И.Е. Волновые процессы. Основные законы / И.Е. Иродов. – 7-е изд. – М. : БИНОМ. Лаборатория знаний, 2015. – 263 с. – ISBN 978-5-9963-1897-1
5. Калитеевский Н.И. Волновая оптика : учеб. пособие для вузов / Н.И. Калитеевский – 2-е изд. М. : Высшая школа, 1978 – 383 с.
6. Ландсберг Г.С. Оптика : учеб. пособие для вузов / Г.С. Ландсберг. – 6-е изд. – М. : Физматлит, 2003. – 848 с. – ISBN 5-9221-0314-8
7. Бутиков Е. И. Оптика : учеб. пособие для вузов / Е.И. Бутиков ; под ред. Н.И. Калитеевского. – М. : Высш. шк., 1986. – 512 с.
8. Михельсон А.В. Волновая оптика : учеб. пособие / А. В. Михельсон, Т.И. Папушина, А.А. Повзнер и др. ; под общ. ред. А.А. Повзнера. – Е. : Урал. ун-т, 2013. – 119с.
9. Киктенко Е.О. О возможности обсуждения эксперимента по стиранию квантовой информации в лабораторной работе по классической оптике / Е.О Киктенко, Н.А. Афонькина, Б.Г. Скуйбин // Физическое образование в вузах. – 2017. – №4. – C. 85 – 94.
10. Bitbucket [Элекронный ресурс] – URL: https://bitbucket.org/iminchenko/opticalexperiment (дата обращения: 28.05.2018).

Список литературы на английском языке / References in English

1. Martinson L. K. Jelektromagnitnoe pole : ucheb. posobie [Electromagnetic field : education manual] / L. K. Martinson, A. N. Morozov, E. V. Smirnov. – M. : Izd-vo MGTU im. N.Je. Baumana, 2013. – 422 p. [in Russian]
2. Fejnman R. Fejnmanovskie lekcii po fizike. V 10 ch. Ch. 6. Jelektrodinamika. [The Feynman lectures on physics. In the 10 h P. 6 Electrodynamics] / R. Fejnman, R. Lejton, M. Sjends. M. : Jeditorial URSS 2004. – 339 p. [in Russian]
3. Sivuhin D.V. Optika [Optics] / D.V. Sivuhin – 3-rd edition – M. : Fizmatlit, 2005. – 792 p. [in Russian]
4. Irodov I.E. Volnovye processy. Osnovnye zakony [Wave processes. Basic laws] / I.E. Irodov. – 7-th edition. – M. : BINOM. Laboratorija znanij, 2015. – 263 p. – ISBN 978-5-9963-1897-1 [in Russian]
5. Kaliteevskij N.I. Volnovaja optika : ucheb. posobie dlja vuzov [Wave optics : manual for university] / N.I. Kaliteevskij. – 2-nd edition. M. : Vysshaja shkola, 1978 – 383 p. [in Russian]
6. Landsberg G.S. Optika : ucheb. posobie dlja vuzov [Optics: manual for university] / G.S. Landsberg. – 6-th edition. – M. : Fizmatlit, 2003. – 848 p. – ISBN 5-9221-0314-8 [in Russian]
7. Butikov E. I. Optika: ucheb. posobie dlja vuzov [Optics: manual for university] / E.I. Butikov ; edited by N.I. Kaliteevskogo. – M. : Vyssh. shk., 1986. – 512 p. [in Russian]
8. Mihel'son A.V. Volnovaja optika : ucheb. posobie [Wave optics : education manual] / A.V. Mihel'son, T.I. Papushina, A.A. Povzner and others. ; edited by A.A. Povznera. – E. : Ural. un-t, 2013. – 119p. [in Russian]
9. Kiktenko E.O. O vozmozhnosti obsuzhdenija jeksperimenta po stiraniju kvantovoj informacii v laboratornoj rabote po klassicheskoj optike [Discussion of the Role of Quantum Information in the Framework of Laboratory Practice on Classical Optics] / E.O. Kiktenko, N.A. Afon'kina, B.G. Skujbin // Fizicheskoe obrazovanie v vuzah [Physical education in universities]. – 2017. – №4. – P. 85 – 94. [in Russian]
10. Bitbucket [Electronicresource] – URL : https://bitbucket.org/iminchenko/opticalexperiment (accessed: 28.05.2018).