К ПРОЕКТИВНЫМ СВОЙСТВАМ ФИЗИЧЕСКОГО ПРОСТРАНСТВА-ВРЕМЕНИ. ЧАСТЬ II. О МЕРАХ И КРИВИЗНЕ В КЛАССИЧЕСКОЙ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО ‒ БОЛЬЯИ

К ПРОЕКТИВНЫМ СВОЙСТВАМ ФИЗИЧЕСКОГО ПРОСТРАНСТВА-ВРЕМЕНИ. ЧАСТЬ II. О МЕРАХ И КРИВИЗНЕ В КЛАССИЧЕСКОЙ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО ‒ БОЛЬЯИ

Научная статья

Пермикин В.С.*

ООО «НПМ «Ньютоника», Екатеринбург, Россия

* Корреспондирующий автор (vladimir.permikin[at]yandex.ru)

Аннотация

В предположении, что 4-х мерное физическое пространство (пространство-время) является проективным, а его геометрия ‒ классической неевклидовой геометрией Лобачевского ‒ Больяи (гиперболической геометрией) рассмотрены следующие задачи: 1) обоснование с помощью проективной геометрии существования в геометрии Лобачевского ‒ Больяи двух основных неевклидовых мер расстояния − аддитивной классической неевклидовой меры и неаддитивной неевклидовой меры, которая является обобщением физического интервала между событиями; 2) вывод формул, описывающих преобразование координат между двумя автополярными системами координат, − рассмотрен случай взаимного расположения двух автополярных систем координат 4-х мерного проективного гиперболического пространства, когда ось времени и одна из координатных пространственных осей обеих систем лежат в одной плоскости, а две другие оси систем соответственно попарно параллельны; 3) обоснование кривизны плоской неевклидовой геометрии как кривизны меры; 4) вывод формул, описывающих изменение со временем расстояния, скорости и ускорения между инерциальными системами в 4-х мерном случае.

Ключевые слова: ускоренное расширение Вселенной, тёмная энергия, геометрия проективная, псевдоевклидова, гиперболическая, неевклидова, геометрия Лобачевского ‒ Больяи, автополярная система координат, Абсолют, вурф, двойное отношение, кривизна меры, гауссова кривизна поверхности.

TO PROJECTIVE PROPERTIES OF THE PHYSICAL SPACE-TIME. PART II. MEASURES AND CURVATURE IN CLASSICAL THE GEOMETRY OF LOBACHEVSKY ‒ BOLYAI

Research article

Permikin V.S.*

LLC “NPM “Newtonic”, Ekaterinburg, Russia

* Corresponding author(vladimir.permikin[at]yandex.ru)

Abstract

Under the assumption that 4-dimensional physical space (space-time) is projective, and its geometry the classical non-Euclidean geometry of Lobachevsky ‒ Bolyai (hyperbolic geometry) the following tasks: 1) the rationale for using projective geometry for the existence in the geometry of Lobachevsky ‒ Bolyai's two main non-Euclidean measures of distance − additive classical non-Euclidean and non-Euclidean non-additive measure which is a generalization of the physical interval between the events; 2) derivation of the formulas describing the transformation of coordinates between two autopolarity coordinate systems - the case of the mutual arrangement of the two autopolarity coordinate systems are 4-dimensional projective hyperbolic space, when the time axis and one spatial coordinate axes of both systems lie in the same plane, and the other two axis systems are pairwise parallel; 3) justification of curvature of the flat non-Euclidean geometry as curvature measures; 4) derivation of the formulas describing the change with time of distance, speed and acceleration between inertial systems in 4-dimensional case.

Keywords: accelerated expansion of the Universe, dark energy, projective geometry, pseudo-Euclidean, hyperbolic, non-Euclidean geometry of Lobachevsky ‒ Bolyai, autopolarity coordinate system, the Absolute, Worf, double ratio, curvature measure, the Gaussian curvature of the surface.

Введение

Данное сообщение является непосредственным продолжением статьи [1], в которой выдвинуто утверждение, что 4-х мерное физическое пространство (пространство-время) является проективным пространством и обладает гиперболической (псевдоэллиптической – по терминологии Феликса Клейна [2, С. 247]) геометрией Лобачевского ‒ Больяи. В [1] показано, что в геометрии Лобачевского ‒ Больяи две инерциальные системы имеют относительное ускорение всегда, даже в момент времени, когда их относительная скорость равна нулю (если такой момент имеется − при компланарности их мировых линий). Но это ускорение не является следствием действия на них каких-либо сил, а является проявлением структуры гиперболической проективной (псевдоэллиптической) геометрии. Две системы инерциальные с массами равными массе Земли, или даже солнечной, находящиеся на расстоянии в мегапарсек (и удаляющиеся относительно друг друга со скоростью 70 км/сек), вполне можно считать гравитационно не взаимодействующими между собой. Если принять, что в реальном физическом пространстве на таких больших расстояниях проявляются особенности гиперболической проективной геометрии, то для описания ускоренного расширения Вселенной не будет необходимости привлекать тёмную энергию.

В качестве основных методов исследования используется методы проективной геометрии. Связано это с тем, что проективный метод позволяет исследовать структуру геометрии в целом, как единого целого [3, С. 206], [4, С. 82]. Проективный метод позволяет рассматривать геометрию не только какой-либо ограниченной области пространства, и не только пространство всей Вселенной, но и целиком все физическое пространство-время как единую физическую сущность.

Об основных мерах в геометрии Лобачевского ‒ Больяи с точки зрения проективной геометрии

В качестве основных мер расстояния между двумя точками на прямой,  в статье [1] рассмотрены две группы неевклидовых мер. Одна из них является классической, т.е. такой неевклидовой мерой, которая обладает свойством аддитивности. В качестве второй основной неевклидовый меры выбрана мера наблюдаемой физической величины расстояния (пространственной длины, длительности интервала времени и величины интервала между событиями). В статье утверждается, что неевклидова физическая мера расстояния является бельтрамиевой функцией [5, С. 193], аддитивной неевклидовой меры расстояния. Для обоснования этого утверждения было использовано имеющееся в псевдоевклидовой геометрии аналогичное соответствие между быстротой − аддитивным аргументом и его бельтрамиевой функцией − скоростью, которая является наблюдаемой физической величиной.

В виду важности вопроса о мерах, как основных геометрических параметрах, ниже приведён способ введения мер расстояния в неевклидовой геометрии с помощью проективных методов без использования, указанной выше аналогии.

Для упрощения рассмотрим 2-у мерный случай − гиперболическую плоскость Лобачевского ‒ Больяи, т.е. ту, которая пересекает Абсолют. Ниже, как и в [1, C. 108, рис. 3], для введения координат используется простейший проективный инвариант «вурф» − упорядоченная четверка элементов, принадлежащих линейно упорядоченному замкнутому образу [6, С. 15], [7, С. 289]. Так же будем считать, что на рассматриваемой гиперболической плоскости уже имеется евклидово мероопределение (евклидова геометрия). Данное предположение позволит нам использовать понятие двойного отношения, выраженное в евклидовых длинах.

Чтобы избежать неопределённости при задании вурфа и вида двойного отношения мы будем придерживаться следующих соглашений:

1. Элементы вурфа будут записываться так, как они упорядочены на носителе в положительном направлении, начиная с элемента, от которого мы определяем расстояние.
2. Выбор пар элементов вурфа при числовом определении расстояния будет выбираться однозначно, в зависимости от рассматриваемой задачи.
3. Далее применяются следующие обозначения: вурф будет записываться в круглых скобках, его числовое значение в квадратных скобках. Если расставлены стрелки, то значит выбрано одно из возможных числовых значений вурфа. Если для числового значения выбрано его представление через двойное отношение, то оно будет записываться в явном виде.

Пользуясь евклидовым мероопределением, определим координаты как расстояния от начальной точки О до проекций точки M на оси a и b с помощью двух вурфов (O, M_a, E_a, B) и (O, M_b, E_b, A) и на их основе двойных отношений, имеющих следующую структуру:

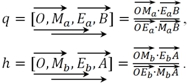   (1)

Будем называть эти координаты нормированными физическими: нормированное пространственное расстояние − q и нормированное время − h.

При таком определении расстояния координаты узловых точек вурфов будут иметь значения:

q_O = 0, q_E = 1, q_B = ∞; h_O = 0, h_E = 1, h_A = ∞.

На оси o с помощью вурфа (A, M_o, E_o, B) аналогично определим третью координату – f, которую будем называть нормированной скорости-подобной координатой точки:

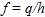
Поскольку построенная система координат автополярна относительно Abs, а сами координаты нормированы относительно точки Е, то уравнение Abs в нормированных физических координатах будет иметь максимально простой канонический вид:

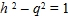
А если на координатных осях выбраны другие отрезки, не связанные с точкой Е, то в ненормированных физических координатах общего вида (x и t) уравнение Abs будет следующим:

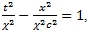
здесь с − скорость света; χ − длина отрезка OE_b в единицах масштабного отрезка оси времени b [1, C. 107 , рис. 3].

Найдем координаты точек пересечения координатных осей с Abs. Координаты этих точек мы будем записывать с индексами в виде римских цифр. Abs пересекает ось времени и ось скорости в их действительных точках, координаты которых в построенной системе координат имеют действительные значения:

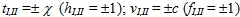
Abs пересекает пространственную ось координат в двух некоторых абстрактных точках, координаты которых имеют мнимые значения: x_II,I = ±iχc (q_II.I = ±i). Здесь изменен порядок точек (маркированных индексами I и II), но мы по-прежнему (как и для осей времени и скорости) считаем, что Abs пересекает пространственную ось в ее положительном направлении в точке с индексом I. Эта перестановка необходима для того, чтобы функциональная связь между аддитивной неевклидовой мерой и неевклидовой физической мерой не зависела от типа точек (действительных или абстрактных), в которых Abs пересекает ось.

Рассмотрим далее два вида вурфов:

(W₁) = (s_O, s_M, s_I, s_II), (W₂) = (s_O, s_M, s_I, s_aO(I,II)),

где s − евклидова координата точки на какой-либо из координатных осей нашей системы  или координата, определенная по правилам (1):

s_O − координата начальной точки O;

s_M  − координата точки проекции  M  на соответствующую ось;

s_I, s_II  − координаты точек I и II пересечения оси с Abs;

s_aO(I,II)  − координата точки, расположенной гармонически (a − от греч. armonikh) точке O  относительно пары точек  I и II (точка, соответствующая точке O в инволюции с двойными точками I и II: на оси b − это точка A, а на оси a − точка B).

Структуру двойного отношения первого вурфа

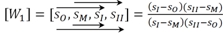   (3)

определим, исходя из требования мультипликативности числовых значений вурфов этого вида:

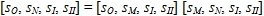
Для второго вурфа структуру его двойного отношения будем считать аналогичной структуре двойных отношений (1), с помощью которых мы определили физические координаты:

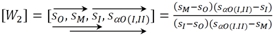   (4)

Можно показать, что между этими двойными отношениями имеется следующая зависимость:

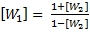   (5)

Вслед за Ф. Клейном [2] в качестве аддитивной неевклидовой меры расстояния мы возьмём логарифм мультипликативной величины [W₁] с некоторым коэффициентом. Обозначим эту аддитивную меру как δ, а коэффициент определим исходя из условия равенства мер δ и [W₂] в малом. Тогда будем иметь следующее соотношение:

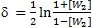   (6)

Исходя из этого общего соотношения, для пространственной оси и оси времени зависимости между их аддитивными и физическими неевклидовыми мерами будут иметь следующий вид:

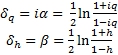
Окончательно для действительных значений мер эти зависимости будут следующими: x/χc = q = tga  и  t/χ = h = thβ

Видно, что физические неевклидовы координаты не обладают свойством аддитивности в отличие от линейных координат евклидовой геометрии. Свойством аддитивности обладают их обратные функции − углы.

После того как найдена связь между аддитивной неевклидовой мерой и неевклидовой физической мерой, определены сами меры, евклидова мера на рассматриваемой плоскости нам больше не нужна. При дальнейших рассуждениях ее можно не использовать.

До нахождения аналитического вида преобразований координат сделаем замечание о метрике углов на проективной гиперболической плоскости. Введенные в [1] меры длины − неевклидова аддитивная мера и неаддитивная физическая мера  полностью применимы для введения метрики углов в пучке прямых. Исходя из свойств полярного соответствия, определяемого Абсолютом плоскости, и справедливости в плоскости малого принципа двойственности, можно считать, что мера угла совпадает с нормированной аддитивной мерой того отрезка поляры вершины угла, на который опирается угол.

В случае эллиптического угла это не совсем очевидно: если вершина угла находится внутри Abs, то для построения вурфа в пучке прямых необходимо принять, что через вершину угла, кроме двух прямых (действительных), угол между которыми мы определяем, проходят также и две абстрактные прямые, которые пересекают поляру вершины угла в тех же абстрактных точках, в которых ее пересекает и Abs.

О преобразовании координат между автополярными системами координат

Имеются различные способы нахождения аналитического вида искомого преобразования. Один из способов, в котором используются координаты узловых точек автополярных систем координат и общий дробно-линейный вид проективных коллинеарных преобразований, применен в [1] для нахождения вида элементарного (поворота вокруг одной из узловых точек) гиперболического поворота. При другом способе, который и описан ниже, используются элементарные, в данном случае гиперболические, повороты и их аналитический вид, выраженный через однородные координаты.

Рассмотрим следующий частный случай взаимного расположения двух автополярных систем координат. Пусть мы имеем две автополярные системы координат, расположенные как показано на рис. 1. Их координатные оси q (ОВ), h (ОА) и q' (О'В'), h' (О'А') лежат в одной плоскости (назовем ее плоскостью ∆), а оси l (ОС), l' (О'С') и n (ОD), n´ (О'D') попарно параллельны, т.е. узловые точки C, C´ и D, D´ попарно совпадают.

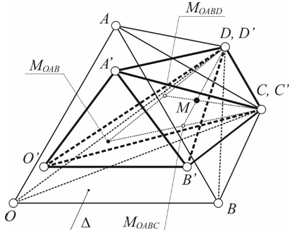
Рис. 1 – Взаимное расположение двух автополярных систем координат OABCD и O´A´B´C´D´

 

В отношении же точки (события) мы считаем, что она принадлежит рассматриваемому координатному пента-тетраэдру (пусть, как показано на рис. 1, это точка M), но не принадлежит никакому одному элементу автополярной конфигурации (узловой точке, координатной линии, координатной плоскости или координатному тетраэдру). Найдем проекцию точки M на плоскость OAB (на рис. 1 это точка М_ОАВ) Для этого вначале спроектируем ее из точки C,C´ (или из точки D,D´) в координатный тетраэдр OABD в точку М_ОАВD (или, соответственно, в тетраэдр OABC в точку М_ОАВC ), а затем из точки D,D´ (C,C´) на плоскость OAB (∆). Поскольку точки C,C´ и D,D´ не участвуют в преобразованиях (переходят сами в себя), то и построенная проекция точки M на плоскость OAB (∆) не зависит от рассматриваемого преобразования координат.

Это обстоятельство позволяет вначале найти преобразование между системами координат, расположенными в плоскости ∆, а затем общее преобразование для остальных двух координат точки M.

Рассмотрим плоскость ∆. Положение в этой плоскости одной из автополярных систем координат (O´A´B´) относительно другой (OAB) может быть задано координатами точки, принимаемой за начало координатной системы (q_O´, h_O´), величиной скорости F_b´ (на рис. 3 это интервал между двумя точками A и N) и направлением времени (одним из двух направлений прямой, на которой лежит ось времени).

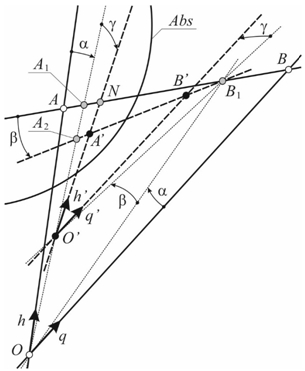
Рис. 2 – Плоскость ∆. Преобразование автополярной системы координат OAB в автополярную систему O´ A´ B´ с помощью трех гиперболических поворотов α, β и γ

 

Искомое преобразование (системы O,q,h в систему координат O´,q´,h´ ) может быть найдено как последовательность (поскольку эти повороты некоммутативны) трех элементарных поворотов, например, трех следующих гиперболических поворотов (см. рис. 2):

1. Поворот системы OAB вокруг точки O на гиперболический угол α до ее перехода в систему OA₁B₁, где:

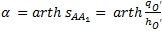   (7)

2. Поворот системы B₁OA₁ на гиперболический угол β вокруг точки B₁ до ее перехода в систему B₁O´A₂, где:

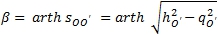   (8)

Общий вид интервала s₁₂ приведен в [1, C. 109, 110, (6), (7)].

1. И поворот на гиперболический угол γ системы O´A₂ B₁ вокруг точки O´до перехода ее в систему O´A´B´, где:

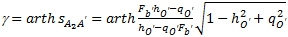   (9)

Переходя от дробно-линейного вида проективного коллинеарного преобразования к линейному виду с помощью перехода от физических координат к однородным (u₁, u₂, u₃) по правилу:

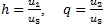    (10)

можно каждому из поворотов сопоставить матрицу размерностью 3х3 коэффициентов линейной системы. Тогда результирующая матрица найдется как их произведение.

Для выяснения как преобразуются координаты точки, не принадлежащие плоскости ∆, рассмотрим преобразование координатного пента-тетраэдра при элементарном повороте. Пусть это поворот вокруг точки O в плоскости ∆. Рассматривая по отдельности пары координатных тетраэдров (см. рис. 3): OABC, OA´B´C, и OABD, OA´B´D можно убедиться, что при элементарном повороте координаты ортогональные плоскости поворота остаются неизменными.

 

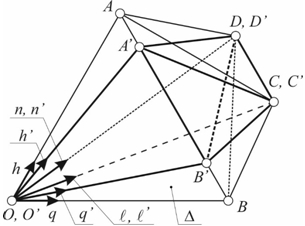
Рис. 3 – Преобразование координатного пента-тетраэдра при элементарном повороте вокруг точки О в плоскости OAB

 

С учетом этого результирующая матрица преобразования однородных координат может быть получена как произведение следующих трех матриц размерностью 5х5:

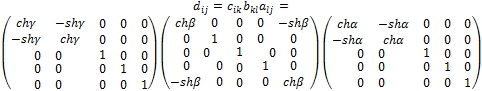
Переходя от однородных координат к физическим, преобразующимся по дробно-линейному закону, после упрощений будем иметь:

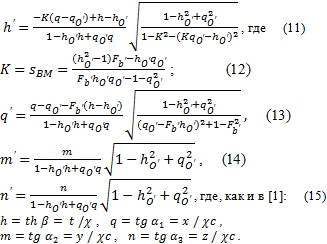
При совпадении начальных точек: О и О' обеих систем координат преобразования переходят в преобразования Лоренца:

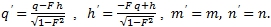
Т. е. преобразования координат точки между двумя системами координат двух систем отсчета, когда их начала отсчета совпадают в псевдоевклидовой и в проективной гиперболической геометриях имеют одинаковый аналитический вид.

Если считать постоянную времени χ бесконечно большой, т.е. перейти к псевдоевклидовому приближению, то преобразования переходят в преобразования Пуанкаре.

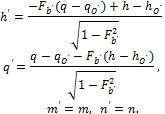
Дополнение к обоснованию понятия «кривизна меры»

Для упрощения изложения мы, как и поступали выше, во-первых, вместо 4-х мерной геометрии рассмотрим ее плоские сечения с эллиптической или гиперболической геометрией; во-вторых, все рассуждения проведем только для метрики точек на прямой и будем использовать нормированные значения мер.

Рассмотрим геометрию как математическую структуру. Можно заметить, что структуры, которые мы называем геометриями, характерны тем, что они в отличие от других математических структур (группы, поля, пространства и проч.) основаны на системах аксиом, обладающих свойством полноты. Непротиворечивую систему аксиом называют полной или категоричной, если любые две ее модели (интерпретации) изоморфны друг другу. Модели называются изоморфными, если между элементами основных множеств (множеств первоначальных элементов) данных моделей существует взаимное одно-однозначное соответствие, при котором соответствующие элементы находятся в соответствующих взаимных отношениях. При рассмотрении какой-либо определенной геометрии можно выделить, по крайней мере, две группы ее моделей. В первую группу входит одна модель – абстрактная, т.е. такая в которой не определяются образы первоначальных элементов. Во вторую группу можно отнести так называемые содержательные модели, первоначальные элементы которых имеют дополнительные геометрические свойства, которые в данной системе аксиом не определяются.

Выше рассмотрена содержательная планиметрическая модель проективной геометрии, носитель которой совпадает с образом плоскости в евклидовой геометрии (как поверхности, внутренняя гауссова кривизна которой равна нулю) дополненной ее бесконечно удаленной (в евклидовом смысле) прямой. Основными первоначальными элементами планиметрии являются евклидовы точки и прямые.

Если рассматривать планиметрическую модель проективной геометрии вложенной в пространственную евклидову геометрию расширенную до проективной (дополненную метрически бесконечно удаленной плоскостью), то с помощью проективного одно-однозначного соответствия можно построить и другие содержательные модели двумерной проективной геометрии.

Одна из таких моделей хорошо известна и была предложена Ф. Клейном в конце 19-го века. В этой модели носителем двумерной проективной геометрии является половинка трёхмерной сферы (см. рис. 4). У этой половинки сферы считаются отождествлёнными противоположные точки окружности, по которой она разрезана. Одно-однозначное соответствие между носителями этих моделей устанавливается с помощью проекции из центра сферы. Сфера касается проективной плоскости, а плоскость разреза сферы и проективная плоскость параллельны (в евклидовом смысле, поскольку в евклидовой геометрии мы всю картину и рассматриваем).

В модели проективной геометрии на полусфере первоначальными элементами являются точки и половинки больших окружностей с отождествленными конечными точками. Эти половинки замещают образы прямых линий абстрактной модели и планиметрической модели проективной плоскости. Половинки больших окружностей сферы имеют кривизну. Такой кривизны нет у прямых абстрактной и планиметрической моделей проективной двумерной геометрии. В модели проективной геометрии на полусфере кривизна присутствует и является неустранимым свойством поверхности (сферы), поскольку поверхность мы представляем в виде гибкой, но нерастяжимой плёнки, вложенной в трёхмерное евклидово пространство.

Кривизна (гауссова) – это свойство данной модели, и при том геометрическое свойство, но никак не свойство проективной геометрии. Из аксиом проективной геометрии кривизна не следует. Проективная геометрия является неметрической геометрией. Это было показано К.Г. Штаудтом в работе [8, С. 49]. Он доказал основную теорему проективной геометрии не используя понятие метрики. Можно дополнить проективную модель на полусфере метрикой этой сферы, тогда получим содержательную модель эллиптической геометрии. Носителем этой модели будет евклидова полусфера.

Используя метрические свойства евклидова пространства, в которое вложена сфера, с помощью коэффициентов первой дифференциальной формы, определяющей квадрат дифференциала длины дуги геодезической, мы можем приписать кривизне числовое значение.

 

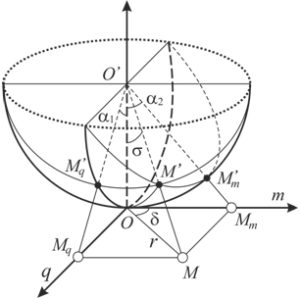
Рис. 4 – Модель Ф. Клейна двумерной проективной и двумерной эллиптической плоскости

 

В планиметрической модели проективной плоскости можно ввести метрику, как показано в [1, С. 108] с помощью полярного проективного соответствия между ее двойственными элементами – точками и прямыми. Можно считать, что между двойственными элементами проективной плоскости существует полярное соответствие и что оно является неустранимым свойством неевклидовой плоскости. Тогда в зависимости от типа полярного соответствия (гиперболического с действительным Абсолютом или эллиптического с мнимым Абсолютом) дифференциальная метрика будет иметь различный вид.

При введении метрики выше и в [1] мы делали предположение, что на рассматриваемой плоскости уже имеется евклидова геометрия. Это позволяло применять понятие двойного отношения отрезков, длины которых могли быть выражены в долях евклидовой меры. Однако, с точки зрения проективной геометрии такой подход не совсем последователен. Действительно, в проективной геометрии, обе системы координат автополярной конфигурации можно ввести независимо друг от друга с помощью инвариантного гармонического свойства полного четырёхугольника. Данный метод введения координат является достаточно трудоёмким, и даже для математических приложений геометрии часто бывает достаточно самого факта существования возможности такого способа введение координат.

С точки зрения классификации геометрий по виду дифференциальной метрики все модели проективной неевклидовой геометрии (модель с гауссовой кривизной, вложенная в евклидово пространство, модель плоской неевклидовой геометрии и абстрактная модель) обладают дифференциальной формой расстояния второй степени. В любой из моделей проективной неевклидовой геометрии можно рассматривать инвариант, называемый кривизной, поскольку все модели между собой изоморфны.

В первой модели инвариантом является гауссова кривизна поверхности второго порядка. Во второй (плоской) модели инвариант будем называть клейновой кривизной меры.

Кривизна меры впервые введена Ф. Клейном [9, С. 272]. Он связывает кривизну плоской проективной неевклидовой геометрии с характеристиками опережения или отставания физической меры по отношению к аддитивной мере при операции измерения одного и того же отрезка. Клейн называет эти меры соответственно специальной соприкасающейся и общей неевклидовой мерой.

Приведем рассуждения Ф. Клейна, немного изменив их.

Рассмотрим проективную эллиптическую плоскость, например, xy или в нормированных координатах qm. Вид дифференциальной метрики (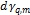), выраженной через декартовы координаты и их дифференциалы, для этой плоскости [1, С. 110, (8)]  при  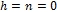  будет следующим:

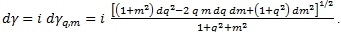   (16)

Преобразованиями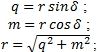

где последнее соотношение следует из [1, С. 110, (7)] и, 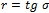, дифференциальная метрика (16) может быть представлена в виде:

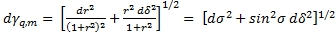   (17)

Здесь σ – это неевклидова аддитивная длина отрезка OM (см. рис. 4), а  δ  – эллиптический угол, который при совпадении инволюций на поляре точки O и на бесконечно удаленной прямой евклидовой плоскости чертежа равен евклидовому углу.

Используя вид дифференциальной формы, выраженный через переменные σ и δ, найдем инвариант «кривизна»:

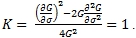   (18)

В соответствии общепринятым обозначением коэффициентов дифференциальной формы:

 

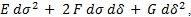
в нашем случае получим .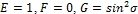

Если рассмотреть ненормированные координаты, то инвариант примет вид:

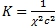   (19)

Пусть эллиптическая плоскость помещена в 3-х мерное евклидово проективное пространство следующим образом: если точка O − начало системы координат эллиптической плоскости, то ее поляра принадлежит бесконечно удаленной плоскости этого 3-х мерного пространства. Свяжем с точкой  начало системы нормированных координат q, m (см. рис. 4).

Пусть в точке O эллиптическая плоскость касается единичной полусферы так, что плоскость разреза полусферы параллельна эллиптической плоскости в евклидовом смысле.

Из центра полусферы – точки 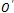 – с помощью прямых можно установить одно-однозначное соответствие между полусферой и эллиптической плоскостью. Рассмотрим дуги геодезических – полудуги наибольших сечений.

С одной стороны дуги имеют евклидову длину, с другой стороны – неевклидову длину в сферической геометрии на полусфере. Если неевклидовы длины расположены на одной геодезической, то обладают свойством аддитивности, поскольку пропорциональны евклидовым углам, в которых они заключены.

Аналогичным образом для гиперболической плоскости с помощью (18) можно найти инвариант «кривизна» .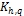

Для гиперболической плоскости дифференциальная метрика имеет вид:

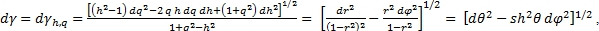   (20)

где: 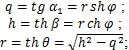как значение выражения [1, С. 110, (8)]  при 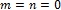. В нормированных координатах 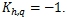В общих ненормированных координатах  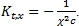   (21) Если единицу измерения времени положить равной единице измерения пространства, то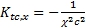

Дальнейшие рассуждения о клейновой кривизне меры приведены в [1, С. 112-113].

Относительные расстояния, скорости и ускорение двух инерциальных систем (4-х мерный случай)

Ввиду большого количества величин необходимых для различения координат и параметров в 4-х мерном случае (в отличие от плоскости) сделаем замечания о применяемых ниже индексах. Верхний левый индекс − буква или цифра будет означать принадлежность параметра (или координаты) к определённой линии. В случае инерциальной системы отсчета этой линией будет прямая. Если этот индекс отсутствует, то значит, что речь идет о какой-то одной, конкретной линии. Нижний левый индекс: его присутствие обозначает, что это фиксированное значение переменной, которое она имеет в какой-то определенный момент времени (обычно принимаемый за начальный), и индекс указывает на этот момент времени; отсутствие индекса говорит о том, что это текущее значение переменной. Правый верхний индекс – если это число, то всегда будет показатель степени, а если штрихи, то они указывают на принадлежность к соответствующей системе отсчета. Правый нижний индекс – если имеется, то обозначает, что параметр, около которого индекс расположен, является проекцией на ту ось, которую обозначает индекс (обычно 1, 2, 3 или соответственно x, y, z); если нет этого индекса, то это означает, что сама величина, которую индекс должен был маркировать, уже обозначена буквой, которой традиционно обозначают проекцию (например, x, y, или z), либо то, что она (величина, параметр) не является проекцией.

Положение мировой линии какой-либо инерциальной системы отсчета, например, l относительно другой инерциальной системы, обозначим ее мировую линию как b, может быть определено с помощью расстояния, момента времени, в который оно измерено, и скорости. В геометрии Лобачевского – Больяи еще необходимо знание времени, когда измерена скорость. Информация о времени измерения скорости необходима ввиду того, что в этой геометрии относительная скорость двух инерциальных систем отсчета со временем не остается постоянной. О том, как изменяется относительная скорость, когда мировые линии двух инерциальных систем компланарны, показано в [1, C. 111, (10)]. В данном сообщении мы будем считать, что скорость и расстояние измерены в один и тот же момент времени, чаще всего принимаемый за начало измерения времени. Прямая l может быть задана двумя своими точками. Будем считать, что одна из этих точек, пусть это точка М, одновременна какой-то точке O прямой b. 

Свяжем с этой точкой O начало системы координат OABCD (см. рис. 5). В этой системе нормированные координаты точки M будем обозначать как, 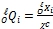, где:  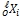− ненормированные координаты, а i = 1, 2, 3 номер пространственной оси − x, y, z, соответственно. Второй точкой прямой l будем считать точку N, которая одновременна точке А, а значит одновременна и точке О. Точка А расположена гармонически точке О начала координат относительно пары точек, в которых прямая b пересекает Abs, и имеет координату t = ∞ (в выбранной системе координат OABCD). В соответствии с одним из основных положений проективной гиперболической геометрии координатами точки N в декартовой системе координат ABCD с началом в точке А будут проекции вектора скорости на оси координат x, y, z [1, С. 105]. Обозначим их как 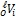, или в нормированном виде как .

 

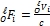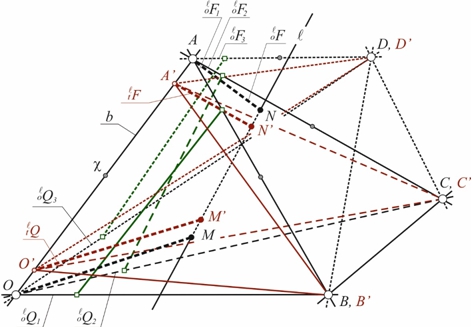
Рис. 5 – Проекции (зеленое) мировой линии l на координатные плоскости основного пента-тетраэдра OABCD автополярной системы координат. Системы координат OABCD (черное) и О’A’B’C’D’ (красное) инерциальной системы отсчета b в два момента времени

 

Рассмотрим проекции прямой MN (l) на координатные плоскости (см. рис. 5).  Для этого спроектируем точку M  на координатные плоскости xOy, xOz, yOz, а затем на оси координат Ox, Oy, Oz. Точку N аналогично спроектируем на координатные плоскости  AСB, ABD и ACD  тетраэдра  ABCD, а затем на координатные оси AB, AD и АС. Соединим прямой линией на каждой из координатных плоскостей AOB (tOx), AOC (tOy) и AOD (tOz) проекцию точки М на ось OB (аналогично OC и OD) и проекцию точки N соответственно на ось AB (AC, AD). В результате мы получили проекции мировой линии инерциальной системы l на основные координатные плоскости системы координат Otxyz инерциальной системы b. Каждая из этих проекций в своей плоскости может быть задана как прямая в «отрезках», но не совсем канонического вида:

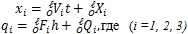   (22)

В любой, следующий за начальным, момент времени t по часам инерциальной системы b отрезок 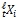 (опуская индекс t, далее будем писать − 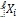), который отсекает на пространственной оси соответствующая проекция прямой l, и проекция скорости на эту ось  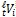(опуская индекс t  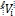− ), будут изменяться по тем же формулам, что и в случае, когда прямые b и l компланарны [1. C. 111, (10), (11)].

Связано это с тем обстоятельством, что в любой, отличный от начального, момент времени  t  по часам инерциальной системы b не изменяют своего положения не только прямая l, но и ее проекции на основные координатные плоскости AOB (tOx), AOC (tOy) и AOD (tOz). Эти плоскости в инерциальной системе b испытывают гиперболические повороты вокруг точек B, C, и D соответственно, и не выходят в другие измерения, т.к. каждая из них проходит через прямую b. С проективной точки зрения система координат OABCD испытывает гиперболический поворот вокруг плоскости BCD, расположенной полярно прямой b относительно Abs.

Воспользовавшись этим результатом и формулами [1, С. 111, (10, 11)] для компланарного расположения мировых линий b и l можно записать формулы для расстояния, скорости и ускорения инерциальной системы l, которые она будет иметь в системе координат, связанной с любым другим  моментом времени инерциальной системы b (ниже во всех формулах  i=1, 2, 3):

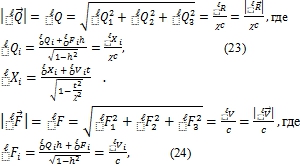
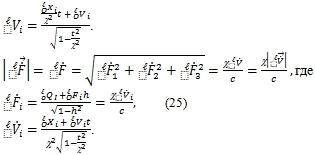
Рассмотрим случай, когда относительно инерциальной системы b движутся две инерциальные системы l и d. Формулы для их взаимных значений расстояния, скорости и ускорения могут быть получены с помощью [1, (3), (6), (7)]. Они имеют вид, который в дальнейшем мы будем называть как вид Фока для модуля вектора в декартовой системе отсчета геометрии Лобачевского ‒ Больяи [10, C. 70]:

Если в эти формулы подставить выражения (23, 24, 25), то получим зависимость расстояния, скорости и ускорения между системами l и d от времени (по часам инерциальной системы b), прошедшего с некоторого момента, принимаемого за начальный.

В заключение данной части статьи заметим, что для того, чтобы иметь возможность рассчитать количественно значение ускорения, скорости и другие параметры необходимо знать величину, введённой в [1] постоянной χ. Определению этой постоянной с помощью ротационных кривых галактик будет посвящена следующая статья.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Пермикин В.С. К проективным свойствам физического пространства-времени. Часть I. Об ускоренном расширении пространства / В.С. Пермикин // Международный научно-исследовательский журнал.- 2017.- № 11(65).- Часть 4.- С.104-115. doi: 23670/IRJ.2017.65.142
2. Клейн Ф. Об интегральной форме законов сохранения и теории пространственно замкнутого мира: [пер. с нем.] / Ф. Клейн // Эйнштейновский сборник, 1980-1981. – М.: Наука, 1985. – С. 226-254.
3. Клейн Ф. Неевклидова геометрия: [пер. с нем.] / Ф. Клейн – 2-е изд. – М.: Едиториал УРСС, 2004. – 360 с.
4. Паули В. Теория относительности: [пер. с англ.] / В. Паули – 2-е изд. – М.: Наука, 1983. – 336 с.
5. Бельтрами Э. Опыт интерпретации неевклидовой геометрии: [пер. с итальян.] / Э. Бельтрами // Сборник: «Об основаниях геометрии». - М.: Изд-во технико-теоретической литературы, 1956. – С. 180-212.
6. Staudt von G. K. Ch. Beitrage zur Geometrie der Lage, Erstes Heftr / G. K. Ch. von Staudt – Nurnberg, Verlag von Bauer und Raspe (Julius Merz), 1856. – 129 s.
7. Глаголев Н.А. Проективная геометрия. / Н.А. Глаголев – 2-е изд. – М.: Высшая школа, 1963. – 344 с.
8. Staudte von G. K. Ch. Geometrie der Lage / G. K. Ch. von Staudt. – Nurnberg: Verlag von Bauer und Raspe (Julius Merz), 1847. – 216 s.
9. Клейн Ф. О так называемой неевклидовой геометрии: [пер. с нем.] / Ф. Клейн // Сборник: «Об основаниях геометрии» – М.: Изд-во технико-теоретической литературы, 1956. – С. 253-303.
10. Фок В.А. Теория пространства, времени и тяготения. / В.А. Фок – 2-е изд. – М.: Изд-во физико-математической литературы, 1961. – 563 с.

Список литературы на английском языке / References in English

1. Permikin V.S. K proektivnym svojstvam fizicheskogo prostranstva-vremeni. Chast' I. Ob uskorennom rasshirenii prostranstva [To projective properties of the physical space-time. Part I. On the accelerated expansion of space] / V.S. Permikin // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. – 2017. – №11(65). Pary 4 – P. 104-115. doi: 10.23670/ IRJ.2017.65.142. [in Russian]
2. Klejn F. Ob integral'noj forme zakonov sohranenija i teorii prostranstvenno zamknutogo mira [About the integral form of the conservation laws and the theory of spatially closed world] / F. Klein // Jejnshtejnovskij sbornik, 1980-1981[Einstein collection, 1980-1981]. – M.: Nauka, 1985. – P. 226-254. [in Russian]
3. Klejn F. Neevklidova geometrija [Non-Euclidean geometry] / F. Klein – 2nd ed. – M.: Editorial URSS, 2004. – 360 p. [in Russian]
4. Pauli W. Teorija otnocitel'nocti [Theory of Relativity] / W. Pauli – 2nd ed. – M.: Nauka, 1983. – 336 p.
5. Bel'trami Je. Opyt interpretacii neevklidovoj geometrii [Experience in interpretation of non-Euclidean geometry] / Beltrami E. // Sbornik: «Ob osnovanijah geometrii» [The collection: "On the foundations of geometry"]. – M.: Izd-vo tehniko-teoreticheskoj literatury, 1956. – P. 180-212. [in Russian]
6. Staudt von G. K. Ch. Beitrage zur Geometrie der Lage, Erstes Heftr [Contributions to the Geometry of the situation, the First Heftr] / G. K. Ch. von Staudt – Nurnberg, Verlag von Bauer und Raspe (Julius Merz), 1856. – 129 p.[ in Germany]
7. Glagolev N.A. Proektivnaja geometrija [Projective geometry] / N.A. Glagolev – 2nd ed. – M.: Vysshaja shkola, 1963. – 344 p. [in Russian]
8. Staudte von G. K. Ch. Geometrie der Lage [The geometry of the situation] / G. K. Ch. von Staudt. – Nurnberg: Verlag von Bauer und Raspe (Julius Merz), 1847. – 216 p. [in Germany]
9. Klejn F. O tak nazyvaemoj neevklidovoj geometrii [About the so-called non-Euclidean geometry] / F. Klein // Sbornik: «Ob osnovanijah geometrii» [The collection: "On the foundations of geometry"]. – M.: Izd-vo tehniko-teoreticheskoj literatury, 1956. – P. 253-303. [in Russian]
10. Fok V.A. Teorija prostranstva, vremeni i tjagotenija [Theory of space, time and gravity] / V.A. Fok – 2nd ed. – M.: Izd-vo fiziko-matematicheskoj literatury, 1961. – 563 p. [in Russian]